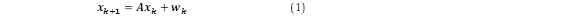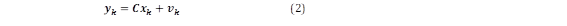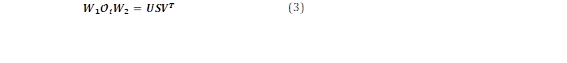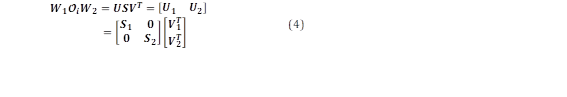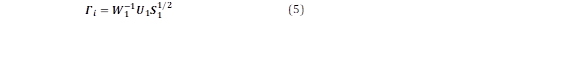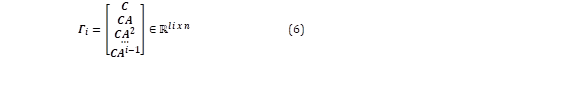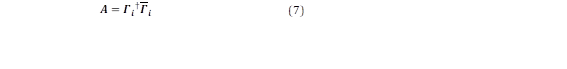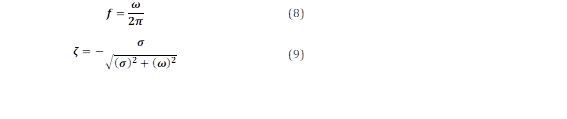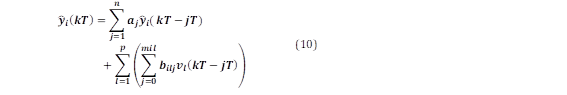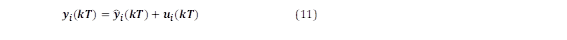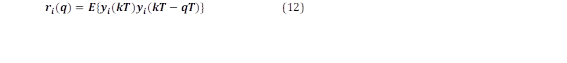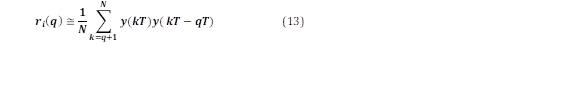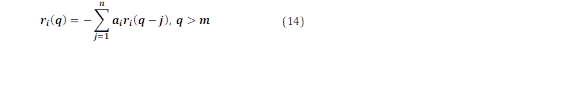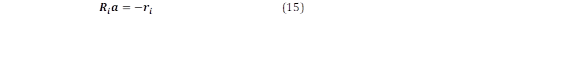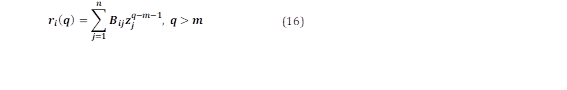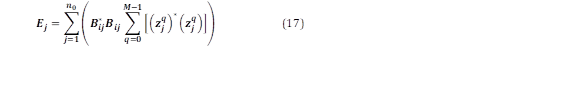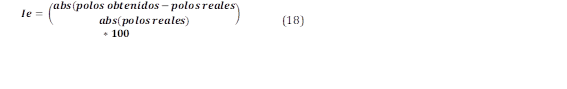INTRODUCCIÓN
En los últimos años, los modernos Sistemas de Suministro de Energía Eléctrica (SSEE) presentan nuevos desafíos como la falta de inversión, envejecimiento de equipos, integración de fuentes de energía renovables intermitentes que producen incertidumbres en la operación y restricciones ambientales para la construcción de nuevas centrales de generación y líneas de transmisión [1]. Estos factores sumados al continuo incremento de la demanda y a la posibilidad de ocurrencia de una gran perturbación podrían conducir a que el estado del Sistema Eléctrico de Potencia (SEP) se desvíe del rango operativo admisible, e incluso ocasionar inestabilidad o apagones a gran escala.
Es así que, resulta necesario monitorear el comportamiento dinámico del SEP, a fin de garantizar y mantener la seguridad y estabilidad de operación [2]. El sistema convencional de Adquisición de Datos, Supervisión y Control (SCADA - Supervisory Control and Data Acquisition) permite el monitoreo sólo del estado estacionario de operación, por su baja tasa de reporte de mediciones, lo que implica que, el comportamiento dinámico del sistema sea desconocido para poder activar acciones de control en casos de bajo margen de estabilidad [3]. Por otro lado, los sistemas de medición de área extendida, (WAMS - Wide Area Measurement Systems), junto con las unidades de medición sincrofasorial (PMU - Phasor Measurement Units) proveen información sincronizada con un periodo de muestreo de 20 [ms] (para sistemas de 50 Hz), lo cual permite monitorear el comportamiento dinámico de los SSEE.
La alta cantidad de información que miden las PMU permite construir una secuencia sincronizada y muy precisa de eventos e identificar y monitorear el comportamiento dinámico de los modos oscilatorios de baja frecuencia (MOBF) que caracterizan la estabilidad de pequeña señal del SEP. Las aplicaciones basadas en registros PMU de manera general se pueden clasificar en de tiempo real y fuera de línea (modo de estudio) [4].
Los métodos de identificación modal a partir de mediciones se clasifican de acuerdo a las características de las señales en la ventana de análisis y corresponden a períodos de grandes perturbaciones (ringdown data) o a períodos con datos tipo ambiente sin grandes perturbaciones (ambient data) y a su formulación matemática como paramétricos o no paramétricos [5]. Para obtener buenos resultados se debe escoger la metodología más adecuada según el tipo de datos a analizar. En este trabajo se aborda el estudio de señales de datos ambiente. Los antecedentes en esta temática reportados en la bibliografía abarcan los estudios desarrollados por los iniciadores del proyecto MedFasee BT Brasil [6] para identificar los MOBF presentes en señales de datos tipo ambiente del sistema brasilero.
El análisis e identificación de MOBF en señales de datos tipo ambiente revela la presencia de un ruido ambiental de nivel constante en el sistema. La hipótesis considerada es que este ruido es el resultado de pequeñas variaciones en la carga, que actúan como excitación de baja amplitud para los modos electromecánicos del sistema. Suponiendo que estas variaciones se modelan como ruido blanco en una ventana de análisis, es posible estimar las características modales de los sistemas a partir de las señales de datos tipo ambiente[7].
Una de las primeras aplicaciones de un método de análisis de datos tipo ambiente se publicó en [8], haciendo uso de un método basado en subespacios estocásticos. Este método estima los modos oscilatorios, sin embargo, no arroja una buena solución al problema de discriminación de modos reales de modos espurios causados por errores numéricos en su técnica matemática.
En [7] se implementan varios métodos de análisis para estimación de modos correspondientes a métodos de análisis de subespacios de estado, entre ellos Análisis de Correlación Canónica (CCA) y Algoritmos Numéricos para la Identificación del Sistema de Espacio de Estado Subespacial (N4SID), con buenos resultados al usar grandes ventanas de datos. En [9] se analiza el efecto de la longitud de la señal y la presencia de ruido para el análisis de datos ambiente con el método de CCA, donde se determina que el análisis requiere de una longitud de ventana de 600 a 900[s]. En [10] se analiza una señal de datos tomando como referencia una ventana que abarca la señal previa y posterior a la ocurrencia de una perturbación, y se la analiza con los método de subespacios de estado y CCA. Los resultados muestran que el método de CCA se desempeña bien en ventanas de datos tipo ambiente.
Por otro lado, los primeros resultados de la aplicación del método paramétrico de YW para la estimación de modos oscilatorios en mediciones tipo ambiente fueron publicados en [11], desde entonces se han venido realizando modificaciones para la estimación de modos oscilatorios en los SEP. Inicialmente, se desarrolló el método para el análisis de una sola señal [12], y posteriormente se modificó para posibilitar realizar el análisis de múltiples señales [13].
En este trabajo se presentan los resultados de una aplicación fuera de línea para la evaluación de la estabilidad de pequeña señal empleando los métodos CCA y YW [9], [14]. Se analizan las señales de frecuencia y diferencia angular de tensión de datos tipo ambiente registrados por las PMU en Baja Tensión (BT) en la red del Proyecto MedFasee BT Argentina. El aporte de este trabajo consiste en aplicar los métodos CCA y YW en mediciones sincrofasoriales en BT para identificar modos oscilatorios poco amortiguados o inestables del SADI.
Este trabajo se organiza como se describe a continuación. En la sección 2, se presenta el proyecto MedFasee BT Argentina. En la sección 3 se presentan las herramientas matemáticas para el análisis de MOBF. En la sección 4 se realiza la parametrización de los métodos de análisis. En la sección 5 se aplican los métodos de CCA y YW a mediciones obtenidas por simulación y a señales PMU de frecuencia y fase de tensión registradas en el Proyecto MedFasee. Finalmente, en la sección 6 se presentan las conclusiones y recomendaciones del trabajo.
PROYECTO MEDFASEE BT ARGENTINA
El Proyecto de investigación científica y cooperación internacional “MedFasee BT Argentina” es desarrollado por cuatro universidades nacionales argentinas, bajo el liderazgo del INESC P&D Brasil y de la Universidad Federal Santa Catarina (UFSC) de Brasil, y en conjunto con otras 21 universidades de Brasil (MedFasee Brasil), 8 de Chile (MedFasee Cono Sur), 2 de Portugal y una de España (MedFasee Ibérico). MedFasee BT Argentina tiene por objeto la implementación de un sistema de medición fasorial sincronizado en baja tensión, para el monitoreo y estudio del desempeño dinámico del sistema eléctrico argentino.
En el marco del MedFasee BT Argentina en el IEE-UNSJ-CONICET se dispone de registros de mediciones de magnitud y ángulo de tensión (fasores) y de frecuencia adquiridos con cuatro PMU instaladas en BT en las Universidades Nacionales de San Juan (UNSJ), de La Plata (UNLP), Comahue (UNCOMA) y Tucumán (UNT), y distribuidos geográficamente en el país.
En el IEE-UNSJ-CONICET la medición de la señal de tensión trifásica de 220[V] a 50[Hz] se realiza con un equipo PMU comercial instalado en la acometida principal del edificio, el cual además de calcular los fasores de tensión y la frecuencia y enviar datos continuamente, a través de Internet, a una tasa de hasta 50 fasores/segundo, al concentrador de datos (PDC) localizado en la UFSC, puede ser configurado para detectar perturbaciones, que producen por ejemplo componentes armónicas en la red y/o caídas de tensión, y para almacenar las correspondientes señales de tensión digitalizadas.
HERRAMIENTAS MATEMÁTICAS PARA EL ANÁLISIS DE MOBF
Análisis de Correlación Canónica (CCA)
El método de subespacio CCA construye un modelo lineal en espacio de estados del que se pueden extraer la frecuencia de los modos y los factores de amortiguamiento aplicando el análisis modal. Este método es válido para la identificación de sistemas puramente estocásticos, sin la presencia de entradas externas [5]. La forma discreta de representación es la siguiente.
donde xk ∈ Rnx1 es un vector de estados, yk ∈ Rlx1 es un vector de salidas, wk ∈ Rnxl y vk ∈ Rlx1 son vectores de ruido del proceso y las medidas A y C son matrices con dimensiones apropiadas
Se considera una secuencia de vectores de salida y0, y1, …, yM, donde yk ∈ Rl x 1 para k = 0, 1, …, M. Con estos datos se construye las matrices de bloque de Hankel extendidas y se calcula su proyección ortogonal con i como el número de filas y l el número de señales.
La descomposición en valores singulares (SVD) se realiza por medio de:
donde W1 y W2 son matrices de peso, U y V son matrices ortogonales, y S es una matriz diagonal que contiene los valores singulares de la proyección ponderada. W 𝟏 = 𝜱 𝒀 𝒇 , 𝒀 𝒇 −𝟏/𝟐 donde 𝜱 𝒀 𝒇 , 𝒀 𝒇 es la matriz de covarianza de la matriz Yf, y W2 es una matriz identidad.
Se define el orden n del sistema, como el número de valores singulares significativos de la matriz S, se opera la descomposición en valores singulares de la siguiente manera:
donde U1 ∈ Rli x n, U2 ∈ Ril x (il - n), S1∈ Rn x n, S2 ∈ R(il - n) x (j - n), V1T ∈ Rn x j y V2T ∈ R(j - n) x j
Con i como el número de filas, j el número de columnas y l el número de señales. Se calcula la matriz de observabilidad extendida (i > n) Γi
Esta formulación se usa en el siguiente paso para obtener las matrices del sistema.
Se obtienen las matrices A y C a partir de la matriz de observabilidad extendida
La matriz A es obtenida por la ecuación (7):
La matriz C está determinada por las primeras l líneas de 𝜞 𝒊 con l cantidad de señales. El interés está en los valores propios de la matriz de estado A, a partir de la cual se obtienen la ecuación característica y los modos de oscilación comunes a las señales formadas por la serie de muestras yj(t).
Las raíces de la ecuación característica representan los modos del sistema en el dominio del tiempo discreto (plano “z”). Estos modos son transformados al dominio del tiempo continuo (plano “s” complejo) para calcular con las ecuaciones (8) y (9) los valores de frecuencia de oscilación y tasa de amortiguamiento de los modos de oscilación.
Análisis de Yule Walker (YW)
Este método es el estimador espectral más común del grupo de métodos paramétricos. El principal supuesto utilizado en el método de YW es que un proceso aleatorio (respuesta ambiental) y puede describirse con precisión mediante un modelo autorregresivo.
Las salidas del sistema se muestrean y el modelo se transforma en tiempo discreto. La forma discreta de representación [15], sigue la forma descrita en (1) y (2). Para la salida, se obtiene un modelo autorregresivo de media móvil (ARMA) escrito con las ecuaciones (10) y (11):
Para i = 1, 2, …, n0 donde n0 es el número de señales de salida medidas, T es el período de muestreo, k es un entero en tiempo discreto, n es el orden del sistema, p es el orden de v, mil es el orden MA para la salida i y la entrada l, aj son los parámetros AR, y bilj son los parámetros MA para las entradas l y salidas i.
La autocorrelación de yi está definida como:
donde E{.} es el operador valor esperado, y q es el operador de desplazamiento en tiempo discreto. Sobre un número finito de puntos de datos, la autocorrelación se aproxima por la ecuación (13).
donde N es el número total de datos. La autocorrelación se puede expresar de la siguiente manera:
La ecuación (14) puede ser expresada en forma matricial, ecuación (15):
Para cada resultado de (15), puede desarrollarse el problema matricial. Las soluciones del sistema son los coeficientes “a” del modelo autorregresivo (AR), los cuales son suficientes para calcular los modos.
Las raíces de la ecuación característica obtenidos en el dominio del tiempo discreto, se transforman al dominio del tiempo continuo, y se obtienen los valores de frecuencia de oscilación y tasa de amortiguamiento.
Análisis de Pseudoenergía
Para realizar una correcta selección de los modos, y determinar qué modos son dominantes y cuales son espurios, se ha implementado el análisis de “pseudoenergía” [16]. Al seleccionar las señales a analizar, el objetivo es utilizar señales que tengan una alta observabilidad del modo de interés y una baja observabilidad para otros modos. La observabilidad se mide en términos de pico en el espectro de potencia o energía en la autocorrelación. Como las señales son aleatorias, no se puede calcular directamente la energía de un modo determinado en el dominio del tiempo. Sin embargo, se puede estimar la "pseudoenergía" de un modo determinado dentro de la función de autocorrelación [16]. Para ello se toma la transformada z de (14) y se resuelve para ri(q) en forma paralela, se obtiene:
donde zj es el j polo en tiempo discreto, y Bij es el residuo para el polo zj y la salida i.
La pseudoenergía del modo j resulta:
Los modos se ordenan según la magnitud de Ej.
PARAMETRIZACIÓN DE LOS MÉTODOS CCA Y YW
Con el fin de parametrizar los métodos de análisis de CCA y YW, se generan 4 señales analíticas tipo ambiente que mantienen los valores de frecuencia y amortiguamiento constantes, pero varían en amplitud y fase. Señales que son muy similares a las señales reales de mediciones PMU. Los valores de frecuencia para los 3 modos son: 0.5, 1.2 y 1[Hz] que corresponden a un modo interárea y dos modos locales, y los valores de amortiguamiento son: 3, 10 y 12[%] respectivamente y distintos valores de amplitud y fase para cada modo. Se generan bajo un ambiente controlado con un modelo desarrollado en Matlab/Simulink.
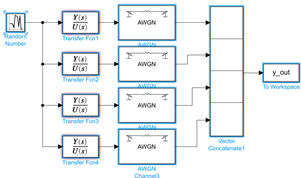
El sistema de pruebas Fig. 1, implementado está compuesto por varios elementos: un generador de números aleatorios con distribución normal (Gaussiana) como entrada al sistema, posteriormente se encuentran los bloques correspondientes a las funciones de transferencia para cada modo donde se puede indicar además de frecuencia y amortiguamiento del modo su amplitud y fase en la señal, a continuación se conecta con un bloque AWGN que añade ruido blanco gaussiano a la señal de salida, en este caso 60[dB], valor de ruido considerado como típico en las mediciones de un sistema eléctrico. Finalmente, las señales se conectan a un bloque que concatena las cuatro señales, las ordena en forma de vectores fila y se exportan para su posterior análisis con los métodos CCA y YW.
Ajuste del orden, tasa de muestreo, tamaño de la ventana y número de filas de las matrices.
Se implementó un modelo de optimización restringida mediante un algoritmo genético el cual tiene como función objetivo la minimización del indicador de error entre los modos de referencia conocidos y los modos calculados por CCA y YW y que de acuerdo a ciertas restricciones y puntos de partida optimiza la parametrización de los dos métodos.
Para hallar los valores óptimos correspondientes al orden y número de filas de las matrices, se determinó como punto de partida un período de 1/10 como submuestreo, es decir una frecuencia de submuestreo de 10[Hz] y una ventana de 600[s]. Estos valores se fijaron en base a estudios previos [9] y a su posterior verificación a través de múltiples simulaciones en distintos escenarios considerando que mientras más extensa es la ventana más se incrementa el tiempo de cálculo sin presentar un cambio notable en la precisión de los resultados el rango de 600 a 900[s]. Los parámetros a determinar son el orden y el número de filas de las matrices de cada método de análisis CCA y YW para el sistema multiseñal implementado en la Fig. 1 y las 4 señales analíticas.
Formulación matemática del modelo de optimización restringida.
Variables de control preestablecidas
x3 = tamaño de ventana[s] =600
x4 = frecuencia de submuestreo [Hz] = 10
Variables de control a determinarse
x1 = orden
x2 = número de filas de las matrices
Indicador de Error
Función objetivo
Minimizar Ie = Min Ie(x1, x2) [%]
Restricciones
10<x1<200
6<x2<100
x1 - x2 = 0
El indicador de error es calculado para cada modo individualmente. Cuando se consideran varias señales los métodos de CCA y YW procesan todas las señales en conjunto y determinan los modos, para posteriormente calcular el indicador de error. La optimización se ha realizado en forma individual y también en conjunto para las 4 señales. Los rangos de las restricciones fueron tomados en base a los estudios realizados en [9], donde se describe que el orden no puede ser menor al doble del número de modos presentes en la señal.
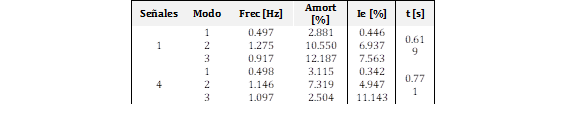
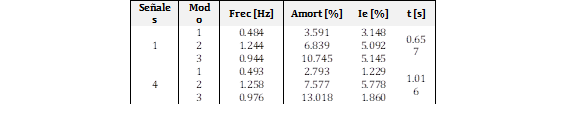
Los resultados para una parametrización óptima según el modelo de optimización restringida se muestran en la Tabla 1 para ambos métodos, CCA y YW. Se puede observar que para cada método de análisis se obtuvieron valores distintos de orden y número de filas.
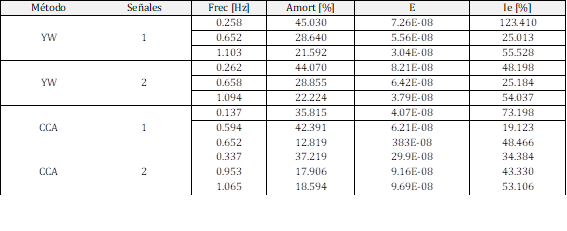
En las Tablas 2 y 3 se presentan los resultados de CCA y YW al analizar 1 y 4 señales, donde se observa que: el método de CCA en el análisis de una señal es mucho más preciso que YW en la identificación de MOBF que presentan amortiguamientos no muy bajos de 10[%] aproximadamente. CCA es preciso en el análisis de una señal si el MOBF es muy poco amortiguado. YW presenta dificultades para separar MOBF que se encuentran muy cercanos como sucede con los dos locales, esto sucede para el análisis de una señal y multiseñal. CCA no presenta grandes cambios en el análisis multiseñal con modos muy cercanos, entonces resulta conveniente usar el método de CCA cuando el MOBF es muy poco amortiguado, menor a 5[%] en análisis de una señal y multiseñal. Por último, el método de CCA en el análisis de una señal es mejor que YW ya que presenta un menor error en MOBF con amortiguamientos menores a 5[%] y también con amortiguamientos de aproximadamente 10[%]. Con respecto al tiempo de análisis en ambos métodos es similar, y aumenta mínimamente al analizar multiseñales.
Preprocesamiento de la Señal
En los sistemas eléctricos las señales presentan variaciones que modificarán los resultados como son el ruido de medición propio de las señales medidas y los datos atípicos, motivo por el cual es necesario un preprocesamiento de la señal con el objetivo de eliminar dichas variaciones y obtener buenos resultados al aplicar los métodos de CCA y YW. En este trabajo el preprocesamiento de la señal consiste en 3 etapas: se realiza un tratamiento de datos atípicos a través de un método de suavizado basado en la regresión cuadrática de LOESS, se elimina la tendencia y se elimina la media de la señal [5], por último se elimina el ruido presente en la señal a través de un filtro pasabanda con frecuencias de corte de 0.1[Hz] y 2[Hz] de diseño FIR (Respuesta al Impulso Finito). Para el cálculo de los coeficientes del filtro FIR se utilizó la ventana de Hanning (también conocida como ventana de Hann) y un orden de 500.
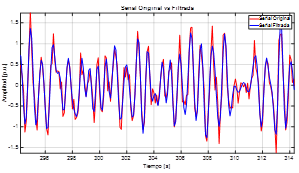
En la Fig.2 se presenta en una pequeña ventana de datos la señal #1 original generada con el modelo y la señal filtrada sin tendencia, valor medio ni outliers. No es posible distinguir el modo de 0.5[Hz] muy poco amortiguado, es por este motivo que se utilizan métodos de análisis como CCA y YW.
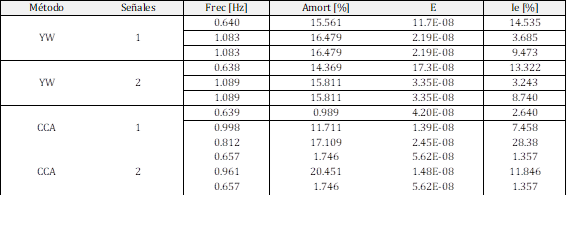
En las Tablas 4 y 5 se presentan los resultados de CCA y YW al analizar 1 y 4 señales previamente filtradas, donde se observa que con el filtrado de las señales los resultados de ambos métodos mejoran notablemente, YW deja de tener dificultades para separar dos modos muy cercanos. CCA es más preciso que YW en el análisis de una señal o multiseñal de MOBF con un amortiguamiento menor al 5[%]. CCA es más preciso en el análisis de una señal si el MOBF tiene un amortiguamiento del 10[%] aproximadamente. CCA no presenta beneficios importantes en el análisis multiseñal en este caso al presentar modos muy cercanos, por este motivo es conveniente usar el método de CCA cuando el MOBF es muy poco amortiguado, menor a 5[%] en análisis de una señal y multiseñal. YW mejora al analizar multiseñales. CCA al analizar una sola señal arroja mejores resultados que al analizar múltiples señales ya que arroja un menor error en MOBF con amortiguamientos menores a 5[%] y también con amortiguamientos de aproximadamente 10[%]. Con respecto al tiempo de análisis en ambos métodos es similar, y aumenta mínimamente al analizar multiseñales.
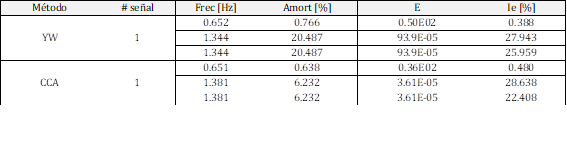
Se ha realizado un estudio adicional con una señal que presenta MOBF con un modo local que tiene bajo amortiguamiento y el modo interárea uno mayor. Se pudo verificar que ambos métodos de análisis CCA y YW calculan bien el modo con menor amortiguamiento, que en este caso es el modo local de 1.2[Hz]. Sin embargo, el CCA calcula mejor el modo interárea.
Con señales reales obtenidas por medición PMU no es posible tener una referencia para calcular un indicador de error. Por tal motivo esta metodología de parametrización permite asegurar una buena precisión de los métodos, desempeño que por extensión se tendrá también al analizar señales reales las que tienen características muy similares a las señales de prueba.
ANÁLISIS DE RESULTADOS MÉTODOS CCA Y YW
Mediciones obtenidas por simulación
Para realizar el estudio de mediciones obtenidas por simulación se utiliza el sistema de dos áreas y cuatro generadores [5] el cual se simuló en el programa Power Factory de Digsilent. Este sistema es ampliamente utilizado para estudios de estabilidad de pequeña señal. Para obtener los datos tipo ambiente se procedió a realizar una variación con una distribución de probabilidad uniforme dentro del rango de ±5% de los valores de potencia activa y reactiva de las cargas, dichas variaciones se realizaron cada 0.001[s] durante una ventana de 600[s], se registraron y guardaron las señales de frecuencia de dos barras, una de cada área, y la señal diferencia de fase tensión entre las barras para su posterior análisis con los métodos de CCA y YW.
La parametrización es: ventana de 600[s], submuestreo de 10[Hz], orden de 20 y número de filas de las matrices de 50 para el método de análisis de CCA y de 14 y 74 respectivamente para el método de YW. Dichos parámetros se obtuvieron por optimización en la sección 4. Para tener una referencia de los MOBF presentes, se realizó el Análisis Modal empleando el programa Power Factory de Digsilent en el estado estacionario inicial para su posterior comparación con los resultados obtenidos por los métodos de análisis de CCA y YW. Se utilizó el método de cálculo QR/QZ que calcula todos los modos presentes en el SEP. La selección de los modos a ser analizados se realizó en función de los modos de interés, que en este caso son los modos interárea y locales, tomando en cuenta sus frecuencias y amortiguamientos.
Se realizó el análisis en dos escenarios: en primer lugar, se simuló el sistema con los 4 PSS activados (E/S) en los 4 generadores, esto ocasiona que el sistema sea muy estable y presente MOBF muy amortiguados. Los modos obtenidos a través del análisis modal se presentan en la Tabla 6.
En segundo lugar, se simuló el sistema con los 4 PSS de los 4 generadores desactivados (F/S), con el objetivo de identificar MOBF poco amortiguados. Para que el sistema no sea inestable debido al amortiguamiento negativo del modo interárea se disminuyó la potencia por la interconexión de ambas áreas. Esto se logró disminuyendo la potencia activa de la carga perteneciente al área que importa energía. En la Tabla 7 se muestran los MOBF obtenidos con el módulo de análisis modal, donde se observan dos modos locales con amortiguamiento aproximadamente del 10% y un modo interárea muy poco amortiguado con amortiguamiento de aproximadamente el 1%.
Se han analizado las señales filtradas de: frecuencia en las dos barras en forma individual y en conjunto para ambos escenarios y diferencia angular de tensión entre barras para el segundo escenario. Se presentan los resultados del análisis con los métodos de CCA y YW en las Tablas 8, 9 y 10.
En la Tabla 8 se presenta el resultado del análisis de señales de frecuencia con los 4 PSS activos, se han extraído los tres MOBF que presentan una mayor pseudoenergía en cada método de análisis. Se observa que, para ambos métodos, cuando los MOBF son muy amortiguados los resultados no son buenos. Los resultados obtenidos presentan errores bastante elevados, el mínimo error que presenta el método de YW es del 25[%] y el máximo del 123[%], mientras que para el método de CCA el mínimo error es de 19[%] y el máximo de 74[%] para los modos locales e interárea. Como se observa en la Tabla 8 los amortiguamientos son mayores al 10[%] por lo tanto no resultan en falsos positivos.
En la Tabla 9 se presenta el resultado del análisis de señales de frecuencia con los 4 PSS F/S de los métodos de análisis CCA y YW, donde se ven reflejados varios cambios. Se observa que a diferencia del escenario donde los PSS estaban E/S, los indicadores de error han disminuido notablemente. El método de YW calcula bien los MOBF locales, presentando errores menores a un 10[%], mientras que para el interárea no arroja buenos resultados. YW mejora levemente al realizar un análisis multiseñal. Se puede notar que el método de CCA a diferencia de YW arroja buenos resultados al calcular los MOBF interárea, presentando errores menores a un 2[%]. CCA calcula de mejor manera cuando se realiza un análisis multiseñal. Por último, el tiempo de cálculo para ambos métodos es similar.
En la Tabla 10 se presentan los resultados de análisis de la señal de la diferencia angular de tensión con los 4 PSS F/S. Ambos métodos CCA y YW, arrojan buenos resultados al calcular los MOBF interárea de muy bajo amortiguamiento, presentando errores menores a 1[%], situación que no sucede con los modos locales, presentando errores de hasta un 28[%]. Con respecto al tiempo de cálculo es similar para ambos métodos.
Se puede concluir que cuando se analizan las señales de frecuencia, el método de CCA tiene un mejor desempeño que YW con modos poco y muy poco amortiguados, además sus resultados mejoran cuando se analizan dos señales en conjunto. Mientras que cuando se analizan señales correspondientes a la diferencia angular de la tensión, ambos métodos calculan con muy bajo error el modo muy poco amortiguado.
Mediciones obtenidas por PMU
Se analizaron con los métodos CCA y YW las señales de frecuencia de las PMU de UNLP y UNCOMA y la diferencia del ángulo de tensión de ambas PMU. Se analizaron señales de 14 ventanas de 30 minutos cada una, ventanas obtenidas cada 3 horas desde las 00:00:00h (hora local de Argentina) del día 18 de febrero hasta las 15:30:00h del día 19 de febrero 2021, y cada ventana se dividió en subventanas de 10 minutos ó 600[s] para identificar el MOBF interárea de muy bajo amortiguamiento de 0.5[Hz] propio del SADI [17], [18].
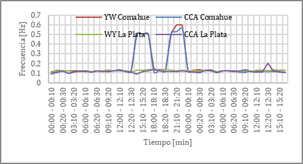
En la Fig. 3 se grafica la frecuencia del MOBF de mayor pseudoenergía obtenido del análisis de las dos señales de frecuencia. Se puede observar que para el análisis de la señal de la PMU ubicada en la UNLP no se identifica el modo interárea de muy bajo amortiguamiento 0.5[Hz] propio del SADI, la frecuencia se mantiene constantemente alrededor de 0.1[Hz] durante todo el tiempo analizado. Mientras que para el análisis de la señal de la PMU ubicada en UNCOMA se puede observar que entre las 15:00 y 15:30 y entre las 21:00 y 21:30 del 18 de febrero CCA y YW calculan el modo interárea de muy bajo amortiguamiento de 0.5[Hz], el resto del tiempo la frecuencia se mantiene alrededor de los 0.1[Hz].
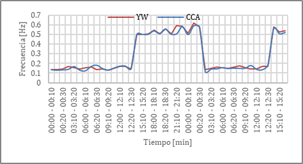
En la Fig. 4 se grafica la frecuencia del MOBF de mayor pseudoenergía obtenido del análisis de la señal de la diferencia del ángulo de tensión de la PMU de UNCOMA respecto a la de UNLP. Se puede observar al igual que en el análisis de frecuencia en la Fig. 3, la mayor parte del tiempo la frecuencia se mantiene alrededor de los 0.1[Hz]. Sin embargo, entre las 15:00 del 18 de febrero y las 00:30 del 19 de febrero los métodos de CCA y YW calculan el MOBF interárea de muy bajo amortiguamiento de 0.5[Hz] propio del SADI. También se puede observar que a partir de las 15:00 del día 19 de febrero nuevamente ambos métodos de análisis calculan el modo interárea de 0,5[Hz].
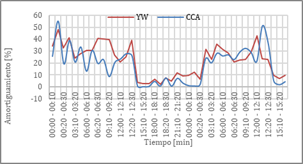
En la Fig. 5 se grafica el amortiguamiento del MOBF de mayor pseudoenergía obtenido del análisis de la diferencia del ángulo de tensión. Se puede observar que los valores de amortiguamiento, para los rangos de tiempo en los cuales se identificó el modo interárea de 0.5[Hz] en el análisis de la de la diferencia angular Fig. 4, oscilan entre el 0.1[%] y 10[%], mientras que para el resto de tiempo el amortiguamiento se incrementa hasta un 55[%].
Es importante mencionar que se han graficado los valores de frecuencia y amortiguamiento de los MOBF que presentaron una mayor pseudoenergía con cada método de análisis. Como se puede observar en la Fig. 3 entre las 18:00 y 18:30 del día 18 de febrero, el modo interárea de 0.5[Hz] no es visible en la gráfica, debido a que éste no presenta la mayor pseudoenergía, lo mismo ocurrió entre las 00:00 y 00:30 de la madrugada, y entre las 15:00 y 15:30 del 19 de febrero. Por esta razón la pseudoenergía no es un indicador completamente confiable para identificar el modo interárea de muy bajo amortiguamiento de 0.5[Hz] propio del SADI [17], [18].
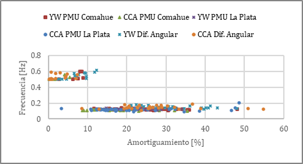
En la Fig.6 se grafican los valores de frecuencia en función del amortiguamiento del MOBF que presenta una mayor pseudoenergía para los métodos de análisis de CCA y YW en las subventanas de 10 minutos de las señales de frecuencia y diferencia angular de tensión. Se puede observar la presencia de MOBF interárea de 0.5[Hz] con bajo y muy bajo amortiguamiento.
CONCLUSIONES
La disponibilidad de información que nos brindan las mediciones PMU ha demostrado ser una fuente importante de datos que permite estudiar el desempeño de los métodos de análisis de datos tipo ambiente, en este caso el método CCA y el método de YW, para identificar los MOBF muy poco amortiguados presentes en el SADI.
Se ha investigado la parametrización de los métodos de CCA y WY en cuanto a orden, duración de la ventana de datos, y número de filas de las matrices a través de la implementación de un modelo de optimización restringida que tiene como función objetivo la minimización de un indicador de error. Al considerar para el sistema un orden mayor al real implica mayor precisión en los modos dominantes poco amortiguados y la aparición de otros espurios, para separarlos se implementó el cálculo de la pseudoenergía de cada modo. El valor de pseudoenergía de los modos espurios es comparativamente bajo en relación con la de los modos dominantes.
Del análisis de la parametrización de los métodos de CCA y YW podemos concluir que para cada uno existe una parametrización apropiada acorde a su desarrollo matemático, al analizar los resultados en la identificación de los MOBF en una señal analítica, YW presenta dificultades para separar modos cercanos. CCA es adecuado cuando el MOBF es muy poco amortiguado, menor al 5[%]. La implementación de una etapa de preprocesamiento y filtrado, es necesaria para una adecuada identificación de MOBF, los resultados mejoran notablemente para ambos métodos. WY deja de tener dificultades para separar modos muy cercanos, sin embargo, CCA es más preciso en el análisis de modos muy poco amortiguados. Ambos métodos se desempeñan mejor al analizar una sola señal y calculan bien los modos poco amortiguados, sean estos locales o interárea, sin embargo, CCA calcula con mayor precisión que YW los modos interárea de muy bajo amortiguamiento que son los que interesa monitorear en mayor medida en los SEP.
Los PSS (Power System Stabilizer) son elementos cuya función básica es agregar amortiguamiento a las oscilaciones del rotor controlando su excitación con señales estabilizantes adicionales. Esto ocasiona que el sistema sea más estable y el amortiguamiento de los MOBF sea más elevado. Es por esta razón que en el análisis de las mediciones obtenidas por simulación con los 4 PSS E/S se observa que el módulo de análisis modal de Digsilent arroja modos con amortiguamientos elevados y al realizar la comparativa con los resultados de los métodos de CCA y YW se puede concluir que ambos métodos cuando los MOBF son muy amortiguados los resultados no son buenos. Cuando todos los PSS del sistema están F/S, el modo de menor frecuencia ha disminuido su amortiguamiento alrededor del 1[%], y al analizar los resultados obtenidos por los métodos de análisis, YW calcula bien MOBF locales, a diferencia de CCA que calcula bien los interárea, y se desempeña de mejor manera en un análisis multiseñal.
Cuando se analizan las señales de frecuencia, el método de CCA tiene un mejor desempeño que YW con modos poco y muy poco amortiguados, además sus resultados mejoran cuando se analizan dos señales en conjunto. Mientras que cuando se analizan señales correspondientes a la diferencia angular de la tensión, ambos métodos calculan con muy bajo error el modo menos amortiguado.
Como se puede evidenciar en el análisis de mediciones obtenidas por PMU los modos con menor amortiguamiento no siempre se encuentran en primera posición en un orden de mayor a menor pseudoenergía, es por este motivo que conviene implementar un proceso de tracking para futuros trabajos.
Se puede evidenciar en el cálculo de los MOBF en el sistema de 2 áreas que el análisis de la señal de la diferencia angular a diferencia del análisis de las señales de frecuencia, arroja mejores resultados en la identificación del modo interárea esta conclusión se puede extender al SADI para identificar MOBF muy poco amortiguados a partir del análisis de señales obtenidas por PMU.