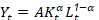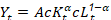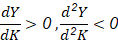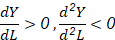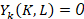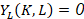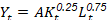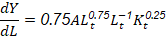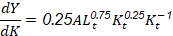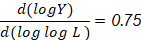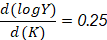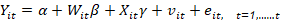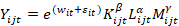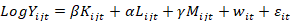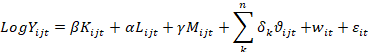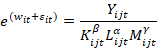Introducción

La función de producción es uno de los principales temas de análisis de la economía neoclásica, particularmente de la microeconomía y su análisis de la teoría de la producción. Implica dar una explicación de cuánto los factores como el capital (maquinaria, equipos, plantas de producción, insumos, otros) y el trabajo que se mezclan en el proceso productivo con una determinada tecnología para producir una mercancía. Sin embargo, no se trata solo de un proceso de cuantificación del aporte de los factores de producción, sino que en esencia está el debate que en economía política se conoce como la lucha de clases entre el patrono como dueño de los medios de producción (capital) y los trabajadores (dueños de la fuerza laboral). Entonces, también el análisis implica la distribución primaria de la renta, o dicho en otras palabras: ¿cómo el valor agregado que se genera se distribuye en salarios para los trabajadores y beneficios para los empresarios?, sabiendo que es imposible generar valor sin que exista esta combinación de factores o aislando por un lado el capital y por otro lado el trabajo (^{Ruiz-de la Peña et al., 2022}).

Según el esquema neoclásico, el empresario paga según la productividad marginal del último trabajador, lo mismo con el capital (^{Mora, 2009}). También, ^{Redondo (2011}) y ^{Bellod (2021}) consideran que asumir este principio significa aceptar que en el conjunto de la economía prevalece la competencia perfecta, información simétrica, perfecta flexibilidad de los precios y salarios que no existen derechos laborales ni bienes públicos, ni tampoco impuestos, subvenciones, ni externalidades y menos aún políticas redistributivas.

^{Segura (1969}), como resultado de su investigación doctoral publica un análisis detallado de las funciones de producción agregadas más conocidas en ese entonces y ahora en la ciencia económica como son: la función de elasticidad de sustitución (CES); la función de Zellner; la función generalizada de Hildebrandy y Liu. Más recientemente, ^{Miller (2008}) realizó una evaluación sobre cuál es la función más apropiada para realizar pronósticos macroeconómicos, si la función de producción de elasticidad de sustitución constante (CES) o la función Cobb-Douglas, y, concluye que esta última es de fácil uso y un buen predictor aun cuando se violan algunos de sus supuestos y que la función CES tiene supuestos menos restrictivos sobre la interacción entre capital y trabajo en la producción, pero las estimaciones de su parámetro de elasticidad han resultado más inconsistentes. El autor plantea que puede no haber razones para preferir una forma sobre la otra, sin embargo, si se busca analizar políticas que afecten el rendimiento de los factores de producción como los impuestos sobre el capital y los impuestos sobre la renta laboral, la estimación Cobb-Douglas puede ser más restrictiva. Entonces, se requiere aplicar y probar cuál permite obtener mejores estimadores (^{Ruiz-de la Peña et al., 2022}).

El esquema neoclásico de la función de producción según la economía, implica relaciones inputs con outputs, es decir factores que son remunerados por la empresa porque permiten producir un bien o servicio. La función sería Q=f(L,K); donde: Q es Producción, L es Trabajo y K es Capital (Pindyck & Rubinfeld, 2013). Entonces, se asume que el trabajo es homogéneo y de hecho lo es cuando la empresa extrae conocimiento y se apropia del mismo a través de la estandarización de procesos y productos, es decir cuando implica acciones repetitivas que se establecen en manuales y guías. Sin embargo, existe también un trabajo que implica innovación y procesos disruptivos que mejoran las capacidades organizativas de la producción empresarial y que rompen este supuesto de homogeneidad (^{Mendoza-Arvizo & Solís-Rodríguez, 2022}).

La función de producción ^{Cobb-Douglas (1928}), quienes plantearon la relación dinámica entre trabajo y capital a través de números índices utilizando mínimos cuadrados ordinarios (MCO) para obtener las elasticidades para ambos factores, considerando rendimientos de escala constantes. Sin embargo, ha recibido duras críticas como, por ejemplo, ^{Durand (1937}), quien cuestionó la aplicabilidad en la vida real de principios como el hecho de que el pago de los salarios sea una función de la productividad marginal del trabajo. Otras críticas se daban por el hecho de obtener una función de producción agregada representativa del conjunto de la economía a partir de microfunciones de producción de empresas o sectores.

Entonces, aparecen también defensores de esta función de producción agregada como el propio ^{Douglas (1948}, 1976), quien agradece las observaciones de Durand y estima nuevamente la función de producción con datos de corte transversal en lugar de series de tiempo y flexibiliza el supuesto de los rendimientos constantes de escala.

Pero entre las modificaciones que se proponen a la función de producción Cobb-Douglas original están las de ^{Brown (1957}), quien cuestiona la información que proporciona los coeficientes en la economía real y propone considerar al tiempo como otra variable. También ^{Moroney (1967}), afirma que se debe tomar en cuenta al clima y al desempeño de los factores (progreso tecnológico) como una variable explicativa y no como el término de perturbación.

^{Bellod (2021}), considera que las regresiones del PIB (Producto Interno Bruto) sobre series de tiempo del empleo y el capital no constituyen una función de producción porque no se puede asumir una misma tecnología para todos los sectores e industrias.

Siguiendo a ^{Brown (1957}) plantea que se trata de una mera identidad contable sobre cómo la renta se reparte para el pago de los factores: 𝑌=𝑤∗𝐿+𝑟∗𝐾; donde Y es la renta nacional; 𝑤,𝑟 corresponde al precio de los factores trabajo (es decir los salarios), y el capital (los intereses). Entonces, esta identidad se cumple porque informa de la cantidad o valoración monetaria del trabajo y el capital (L, K).

Por otra parte, no siempre se tiene que cumplir que la producción (Y) sea la máxima que se puede alcanzar con una dotación de combinaciones de trabajo (L) y capital (K). Así, cuando se construyen series temporales con estas tres variables (Yt, Lt, Kt), se puede garantizar que corresponden a la identidad contable de la renta, pero no necesariamente a la función de producción linealmente homogénea.

Sin embargo, se continúa aplicando la función de producción y proponiendo mejorar la estimación por ejemplo a partir de funciones de costos para eliminar la multicolinealidad presente en el modelo original (^{Praveen et al., 2019}; ^{Mahaboob et al., 2019}). En la misma línea, también se ha propuesto la Función Cobb-Douglas de Elasticidad Variable con la finalidad de considerar el progreso técnico y los tipos de rendimiento a escala (^{Reynés, 2019}). Otros autores han continuado en la línea de modificar las variables originales de trabajo y capital por variables aproximadas y variables de control como es el caso del aporte en el 2009 de Wooldridge.

Frente al debate sobre si la función de producción Cobb-Douglas realmente es apropiada para interpretar las fuentes de crecimiento, así como estimar la productividad de los factores para conocer el desempeño de la producción de un país, es decir si existen o no brechas productivas entre los sectores y territorios. Entonces surgió, la pregunta: ¿cuáles son las principales características de la función de producción Cobb-Douglas y cuán utilizada y apropiada puede ser según los autores para utilizarla en profundizar el conocimiento de la producción de un país o sector de la economía?

Por ello, el objetivo de este estudio es conocer las características, limitaciones y metodologías que se han utilizado para aplicar la Función de Producción Cobb-Douglas según los principales estudios publicados al respecto.

Revisión de la Literatura

Un tema central del estudio de la economía es la producción de bienes y servicios. La actividad de producción se efectúa por ciertas unidades productivas llamadas empresas, esta actividad se lleva a cabo con factores de producción: Trabajo (L), Capital (K) y tierra (t); con un nivel de tecnología (T) dado.

Es importante comenzar planteando algunas definiciones de la función de producción. Para ^{Vargas Biesuz (2014}), la función de producción muestra las distintas cantidades de producto que se puede obtener combinando distintas cantidades de factores productivos y dado ciertos niveles de conocimiento o tecnología.

Entonces, se puede decir que es una especificación de cómo se comporta una cantidad de salida (producto) en función de los insumos utilizados en la producción, este concepto se puede aplicar a nivel de empresas, industrias, individuos o economías enteras. ^{Cobb y Douglas (1928}) sugieren que para entender el cómo se da el volumen de producción física de una determinada industria se requiere: 1) medir los cambios del trabajo y capital que han sido usados para producir bienes; y 2) determinar cuál es la relación existente entre trabajo, capital y producto.

^{Jiménez (2017}) menciona que la función de producción es el insumo principal para determinar la oferta agregada de bienes y servicios y la define como la cantidad máxima que se puede producir con una combinación de factores de la producción, dada una tecnología, en la que cada empresa tiene la suya. Entonces, bajo el supuesto que las funciones de producción individuales son las mismas, se puede obtener una función de producción agregada.

La función de producción Cobb-Douglas tiene que cumplir tres condiciones:

Rendimientos constantes a escala: un aumento de los factores de producción en una determinada proporción implica un aumento equivalente en el nivel de producción dada la tecnología.

Si se tiene la función de producción:

Ecuación 1:

Donde:

𝑌 es el nivel de producción de la economía,

𝐾 es el factor Capital

𝐿 es la dotación del factor trabajo, mientras que el subíndice t hace

referencia al tiempo.

Si se multiplica por una constante c el Capital y trabajo en la ecuación (1), se tiene:

Ecuación 2:

En este sentido, si los factores de producción aumentan c veces, la producción aumentará c veces también.

Los rendimientos marginales de los factores son decrecientes: la productividad marginal del capital (K) y trabajo (L) son positivas pero decreciente, es decir, que cada vez aporta menos a la función de producción.

Para el capital,

ecuación 3:

Para el trabajo,

ecuación 4:

Cumple las condiciones Innada: el producto marginal de los factores tiende a infinito cuando el factor tiene a cero, y tienden a cero cuando el factor tiende a infinito.

Para el capital (K),

ecuación 5:

Para el trabajo (L),

ecuación 6:

Los orígenes del trabajo de la función de producción ^{Cobb-Douglas se remontan al trabajo seminal de Cobb y Douglas (1928}). Limitándose al sector manufacturero estadounidense, los autores quisieron demostrar que los rendimientos constantes a escala eran característicos de esa industria, por lo que propusieron eliminar la posibilidad de presentar rendimientos crecientes o decrecientes. En cuanto a la obtención de los datos, es interesante mencionar que, para la variable capital, no consideraron el capital de trabajo (activos de corto plazo de las empresas) ni la tierra, porque no eran causas del proceso de producción, sino un resultado; y, se tomó en cuenta como capital la maquinaria, herramientas, equipos y edificios de fábricas. Para construir la base de datos de su investigación, los autores trabajaron con series de tiempo, durante un período de 24 años desde 1899 a 1922. Así mismo, ellos estudiaron las elasticidades de la oferta de trabajo y de capital y cómo estas variaciones afectan a la distribución de los ingresos (Douglas, 1934).

Para comenzar, los autores realizaron un gráfico en escala logarítmica del producto, trabajo y capital fijo, ellos notaron que la curva de producción está entre las curvas de los factores de producción y tendían a ser un cuarto de la distancia entre las curvas de los dos factores. La relación dinámica entre trabajo y capital, puede expresarse a través de la división del índice relativo de la oferta de trabajo, por el índice relativo de capital fijo. En consecuencia, utilizaron numerosos índices para la investigación.

Con todo este planteamiento en mente y utilizando Mínimos Cuadrados Ordinarios y la base de datos, en su manuscrito estimaron las elasticidades para el trabajo y el capital, siendo de 0,75 para el primero y 0,25 para el segundo. Esta estimación la realizaron imponiendo rendimientos de escala constantes en términos per cápita. A continuación, se tiene los resultados de la función de producción que obtuvieron:

En la ecuación 7 se visualiza el resultado de la función de producción Cobb-Douglas para los Estados Unidos.

Ecuación 7:

En la ecuación 8 está expresado el Producto Marginal del Trabajo.

Ecuación 8:

El Producto Marginal del Capital se visualiza en la ecuación 9:

Ecuación 9:

La Elasticidad del Trabajo y Capital se puede ver en la ecuación 10 y 11, respectivamente.

Ecuación 10:

Ecuación 11:

Sin embargo, esta famosa función de producción recibió duras críticas, como en el caso de ^{Durand (1937}) en su obra titulada Some thoughts on Marginal Productivity, with special Reference to Professor Douglas Analysis, quien fue el primer autor en brindar una respuesta relevante a la función original planteada en 1928 y 1934 por Cobb-Douglas, sobre todo al artículo publicado por Douglas (1934) titulado The theory of Wages, ya que explica que la misma puede probarse en condiciones específicas pero sus propiedades la vuelven restrictiva. Además, indica que cuando los principios de productividad se extienden a problemas prácticos se hacen todavía más evidentes las limitaciones de este modelo.

Siempre existe una pequeña posibilidad de incrementar la producción sin incrementar la cantidad de insumo, y no considerar esa posibilidad provoca que el análisis carezca de gran exactitud. El autor añadió que, si se analiza detenidamente la producción de una empresa o sector, esta no depende únicamente de su cantidad de insumos disponibles, sino también de las acciones de otras empresas y de los cambios de sus factores productivos, por lo que la función de Cobb-Douglas es poco realista y limitada en aplicaciones prácticas ya que se utiliza a través del teorema de Euler.

Los supuestos de esta función, que ya fueron abordados en el presente texto, con frecuencia no se cumplen en una economía real, además Durand plantea que no se debería asumir una función de producción lineal homogénea, en su lugar, se debe considerar que a medida que una empresa se expande pasa de rendimientos crecientes a rendimientos decrecientes. Por esa razón, no tendría validez afirmar que la industria se maneja a través de rendimientos constantes de escala. El autor propone una fórmula más general, en la que los exponentes de capital y trabajo no necesariamente sumen uno, y el exponente del capital sea una variable, en lugar de una constante.

Es el caso de ^{Mendershausen (1938}), que en su artículo titulado “Production Functions: Cobb-Douglas, Interfirm, Intrafirm”, sostiene que en la función Cobb-Douglas original no se tiene en cuenta las variaciones de aquel capital que ya fue utilizado, en diferentes puntos del período analizado. Afirma que cada variable genera una dependencia con las perturbaciones o errores del modelo y, por esta razón, no se puede interpretar la variación de cada factor como una función lineal del otro. Otro punto tratado por este autor, es la utilización de series de tiempo, destacando que la empleada para representar el capital es únicamente una estimación.

Además, recalca que, al incluir escasas observaciones, es lógico que la relación entre las tres variables sea accidental. Suponer que cada insumo posee un grado constante de intensidad de uso, que no existe progreso tecnológico, ni tampoco cambios en la eficiencia de la productividad cada año, pone en duda el realismo de la función. El error radica, entonces, en pensar que una industria puede reflejarse en una función de producción constante, cuando en realidad, los cambios en los factores provocan desplazamientos sucesivos entre distintas funciones de producción.

Otros autores realizaron aportes a la función original, como ^{Bronfenbrenner (1944}), quien expresó que, al asumir que existe competencia perfecta y rendimientos constantes de escala, se imponen ciertas restricciones. Estos conceptos no se aplican a todas las funciones de producción entre empresas, independientemente de su forma funcional. Considera que los resultados de ^{Cobb y Douglas (1928}), fueron diseñados justamente, para verificar la teoría que inicialmente planteada.

Con esto en mente, el autor propone una función de producción Cobb-Douglas ajustada, donde la participación del trabajo ya no es constante, y viene representada por 𝑘𝐿 𝑄´ , donde Q' es el valor calculado de la producción. Esto demuestra que, el trabajo varía de un punto a otro dentro de la muestra, por lo que es una suposición bastante realista, y se puede aplicar de la misma forma para el capital.

La respuesta a los artículos hasta ahora recopilados, es bastante interesante. De acuerdo con ^{Douglas (1948}), bajo competencia perfecta, cada empresa tiende a nivelar su producción, hasta el punto en que la tasa de rendimiento es constante. Douglas agradece la sugerencia de ^{Durand (1937}), y estima nuevamente la función de producción, con las siguientes modificaciones: la suma de los exponentes puede ser mayor o menor que la unidad, por lo que ya no presiona a la función, a adoptar rendimientos constantes de escala. Además, se reemplazan las series de tiempo, por datos de corte transversal entre industrias en una economía dada, para años específicos.

Es importante aclarar que, en esta ocasión, se utilizaron cantidades físicas de los insumos en lugar de números índices y se incluyó un nuevo concepto financiero como es el de capital-trabajo. ^{Douglas (1948}) defiende nuevamente su función, explicando que la relación entre la producción y los factores productivos no es accidental, pues de lo contrario mostraría resultados muy variables. Niega que el problema radique en el número de observaciones, resaltando que su base de datos es amplia, recolectada de distintos años y países. Expresa, además, que no encuentra el problema de aplicar la función de producción Cobb-Douglas tanto en un ámbito micro como macroeconómico, ya que, en su opinión, los problemas de la economía en su conjunto reflejan los de la industria.

Aunque parece que el estudio de ^{Douglas (1948}) corrigió varias deficiencias de la investigación inicial, eso no fue impedimento para que más autores cuestionaran la verosimilitud de su función de producción. Según ^{Brown (1957}), la función Cobb-Douglas no puede representar la realización estadística de una función de producción. Esto debido a que, no proporciona los coeficientes en la economía real, y si lo hace, es por pura coincidencia. Propone que la función puede lograr un mejor ajuste colocando el tiempo como una tercera variable independiente.

Para ^{Simon y Levy (1963}), el hecho de que los valores estimados de capital coincidan con los valores de capital real, no implica que la verdadera forma de la función de producción sea Cobb-Douglas. Plantean que, en realidad, debería adoptarse una función lineal simple mucho más general que la función original.

Con el tiempo, la función Cobb-Douglas original se ha ido ajustando mediante la incorporación de otras variables. Por ejemplo, ^{Moroney (1967}), afirmó que factores como el clima o el desempeño de los factores, no deben estar incluidos en el término de perturbación, sino evidenciados como variables dentro de la función de producción. Propuso, por lo tanto, una función modificada en la que los insumos son independientes de las perturbaciones y el progreso tecnológico puede cambiar. Las variables del modelo son: V, que es el valor agregado de la industria, X1 es el stock de capital bruto, X2 horas-hombre y X3 horas-hombre asociadas al trabajo no productivo.

De la misma manera, durante la década de los 70, se publicaron algunos artículos que presentaron modificaciones con respecto a la famosa función original. ^{Ulveling y Fletcher (1970}) mencionan que se pierde información relevante, cuando se estima una sola función de producción, pues al existir varias técnicas de producción en una industria en concreto, es posible que las elasticidades de producción y los retornos de escala, no sean constantes. Proponen estimar funciones separadas para cada técnica de producción, con rendimientos variables a escala. Se hace evidente que la escala es mayor, para aquellas técnicas que son más intensivas en capital.

En medio de este escenario, Douglas (1976) defendió la función de producción Cobb-Douglas una vez más, alegando que ningún autor pudo presentar una crítica relevante a su investigación con datos de corte transversal, sino únicamente al original con series de tiempo. Señala que ninguno de sus estudios, ha rechazado la presencia de rendimientos constantes de escala en el sector manufacturero, por lo que no pueden ser descartados con tanta facilidad.

Si bien muchos autores comentaron sobre el tema de rendimientos de escala, o elasticidad de producción constante, ^{Sandelin (1976}) fue el primero en cuestionar el supuesto de la productividad marginal positiva y decreciente. Argumenta que, si bien es cierto que una unidad adicional de insumo disminuye el producto marginal, también lo hace con el total; porque llega un punto, en el que añadir más factores es perjudicial, y disminuye el volumen de producción.

Paralelamente, ^{Charnes et al. (1976}), sugirieron una función homogénea extendida, con elasticidades de producción positivas, pero no necesariamente constantes. La modificación principal que resalta, es que la elasticidad de producción, depende de la relación de la i-ésima entrada de factor, con el producto total.

Para finales de la década, ^{Samuelson (1979}) estableció que Cobb-Douglas es una función poco realista, específicamente por el supuesto de competencia perfecta, opinión que comparte con ^{Bronfenbrenner (1944}). Trabajar bajo el supuesto de competencia perfecta en todos los mercados, es lo mismo que asumir que, todos los consumidores poseen los mismos gustos y preferencias, y destinan su dinero a adquirir los mismos bienes y servicios, al mismo precio. Expresó de esta manera, que las variaciones en los factores de una industria, no pueden ser proporcionales a aquellas presentes en la economía. Los resultados de Cobb-Douglas son una conclusión predeterminada, justamente por la naturaleza de la metodología estadística.

Intrigado por la relevancia que había adoptado la función, ^{Labini (1995}) expuso sus ideas sobre la misma. Planteó que los supuestos de la función Cobb-Douglas, se encuentran sumamente alejados, de las características de la realidad económica de ese entonces, y que los estudios estadísticos de series de tiempo, siempre deben tomarse con escepticismo. Propuso un enfoque dinámico multisectorial, el cual no presenta rendimientos de escala ni elasticidades constantes, ya que el crecimiento es un proceso desigual. Además, la tecnología se representa como una variable endógena, que depende de una tendencia creciente de la producción.

^{McCombie (1998}) se percató de una situación, que los autores anteriores pasaron por alto. En su obra, explica que, si se repite la función original con series de tiempo, la regresión presenta problemas de heteroscedasticidad y multicolinealidad. Al no solucionar dichos problemas, la regresión recae en un sesgo de especificación, y no se encuentra ajustada correctamente. Tal como ^{Labini (1995}), afirma que es un error suponer una tecnología es constante, y considera que este tipo de función, solo es viable en un análisis microeconómico, ya que es bastante cuestionable representar a toda una industria, en una sola función de producción.

Al iniciar una nueva década, los autores se volvieron más conscientes de los cambios que debían aplicarse para mejorar la forma funcional Cobb-Douglas, y adaptarla a una ciencia social tan dinámica, como lo es la economía.

En pleno siglo XX, se continúa realizando ajustes y críticas a la función de producción Cobb-Douglas, así, por ejemplo, ^{Lloyd (2001}) y ^{Balistreri et al. (2003}) comparten el argumento de que esta función probablemente sea cercana a la de Cobb-Douglas, únicamente si se aplica a una economía en estado estacionario, es decir que el stock de capital y población es constante (^{Mankiw et al., 1992}). De esta manera, no crece en el transcurso del tiempo, por tanto, ni los factores ni la producción presentan con claridad sus variaciones, y no se asemeja en ningún sentido a una función de producción realista.

En este mismo sentido, ^{Antràs (2004}), expresa que una función de producción agregada Cobb-Douglas puede llegar a ser engañosa, debido a que no toma en cuenta algunos aspectos relevantes. En primer lugar, el tamaño de la población y los cambios en los salarios, influyen significativamente sobre la oferta de trabajo, y esto influye sobre la variación del factor trabajo. Además, en la función original, no se realizaron pruebas de estacionariedad en las series de tiempo utilizadas, por lo que, si no presentan dicha característica, no se les puede considerar estimaciones consistentes.

Mientras que la mayoría de autores se centraron en modificar la función de producción, proponiendo nuevas variables o enfoques, ^{Felipe y Adams (2005}) dejan bien claro que, para ellos, lo único que hace la estimación de la función Cobb-Douglas, es reproducir la identidad contable del ingreso, distribuyendo el valor agregado, entre salarios y ganancias. Además, expresan que nunca se ha demostrado que el precio del capital y los salarios sean constantes, ni que los mercados sean perfectamente competitivos, por lo que esta función presenta sesgos desde su estructura.

^{Hájková y Hurník (2007}) demostraron que la función de producción agregada de una economía convergente, no puede ser de la forma Cobb-Douglas, debido a que no presenta un crecimiento económico estable, a lo largo del tiempo. Por su parte, ^{Aiyar y Dalgaard (2009}) propusieron una función de producción más general, en la cual el cambio tecnológico sea representado como una variable, y no una constante. Afirmaron que, Cobb-Douglas no es una mala aproximación del crecimiento económico, pero su desventaja, radica en darle demasiada importancia a los factores productivos.

A pesar de todas las críticas hacia el supuesto de rendimientos constantes de escala por varios autores, ^{Felipe y McCombie (2011}) indican que dicha propiedad no es arbitraria, ya que en realidad depende de qué empresa, industria o economía esté siendo analizada. Concluyeron a su vez, que la forma Cobb-Douglas, es en realidad una relación de comportamiento entre factores y producción, y no una función de producción como tal.

De la misma manera, ^{Carter (2011}) comparte el argumento de ^{Felipe y Adams (2005}), describiendo a Cobb-Douglas como una función de distribución del ingreso, y no como una función de producción precisamente, ya que no refleja las innovaciones tecnológicas presentes en la economía. ^{Biddle (2012}) por su parte, consideró que la función brinda una buena explicación de la relación de largo plazo entre trabajo, capital y producción, pero no de las fluctuaciones cíclicas, presentes en la utilización del trabajo y capital.

A lo largo de los años, se presentaron algunas modificaciones a la función original, como se pudo evidenciar con los autores mencionados hasta este punto. Sin embargo, una de las modificaciones más interesantes, es la propuesta de ^{Cheng y Han (2014}), la cual añadió variables ficticias en diferentes etapas. Dichas variables representan el período en el que el Estado implementa nuevas políticas o reformas económicas, así como épocas caracterizadas por desastres naturales. De esta manera, se obtiene un modelo más realista, con un error estándar más bajo que en la función original.

^{Stijepic (2015}) hace énfasis en un aspecto importante, que debe tenerse en cuenta. No todos los sectores utilizan la misma tecnología, por lo que cada sector tiene parámetros específicos. Debido a esto, la función de Cobb-Douglas puede no ser útil para algunas industrias, pero en el caso de otras, puede ser una muy buena estimación. En el caso que se busque estimar una función de producción para varios sectores, considera que se debe incluir una nueva variable: la reasignación de mano de obra entre sectores.

Otro autor que propuso modificaciones en la función original es ^{Apostolov (2016}), quien, en su investigación, representó al factor capital, a través de la inversión extranjera directa (en países receptores), porque es la fuente principal de capital de las empresas. Explica que aumentar dicha inversión, genera cambios positivos en el progreso tecnológico, por lo que, no podría considerarse constante, además que incrementa la producción, las exportaciones, y reduce el desempleo.

Materiales y Métodos

En este trabajo de investigación se realizó una revisión de literatura aplicando una metodología histórica, analítica y descriptiva sobre la teoría publicada desde 1939 hasta 2023. Con base en el método PRISMA 2020 (^{Page et al., 2021}) se realizó la búsqueda y selección de documentos entre marzo y junio de 2022. Esta se complementó con una actualización realizada en abril de 2023.

En un primer momento se analizaron los documentos originarios del modelo y luego utilizando como término clave “Cobb-Douglas” en las bases de datos Scopus, Redalyc, Scielo, Sage journals, Ebsco y DOAJ se encontraron un total de 22 780 resultados. Para refinar la búsqueda se incluyeron los términos “productivity” y “production factors” que al ser combinados con el anterior generaron 428 resultados escritos tanto en castellano como en inglés. Se eliminaron algunos documentos que se repetían en las bases de datos consultadas.

Una vez identificados los documentos, se ordenaron cronológicamente y según su número de citas, luego se filtraron a partir de la lectura de los títulos y resúmenes para llegar a una selección de documentos que fueron leídos íntegramente y fichados, mediante su interpretación y contextualización se construyó un registro bibliográfico en el que se incluyó datos sobre objetivos, metodología, resultados, discusión y conclusiones. Esto sirvió como insumo para analizar los resultados de cada documento y su compatibilidad con el objetivo de esta investigación.

Inicialmente, se tomó una muestra de 72 documentos de la que se descartaron aquellos que no aportaron al cumplimiento de los objetivos. Finalmente se seleccionaron 59 artículos indexados que, sumados a tres libros y a los artículos originales, dieron como resultados las 66 referencias que constan al final de este documento de investigación.

Análisis y Resultados

En este apartado se sintetizan los argumentos a favor y en contra de la función de producción Cobb-Douglas como un buen estimador de la relación entre factores productivos y producción. Se pone énfasis en el hecho de que se ha utilizado para los análisis microeconómicos y macroeconómicos, de modo que es un punto de partida para abordar el crecimiento económico. Además, se sintetiza cómo trabajan los autores con qué datos (transversales o series de tiempo), las variables utilizadas y modelo econométrico. Por supuesto, también se señalan los principales resultados y aplicaciones.

Resultado 1. Cuestionamiento y aplicaciones a la función de producción Cobb-Douglas

Aunque parezca difícil de concebir, en la actualidad, se siguen publicando artículos que cuestionan y aplican a la función Cobb-Douglas, en sus investigaciones. Es el caso de ^{Praveen et al. (2019}) y ^{Mahaboob et al. (2019}), quienes señalaron que se debe estimar esta función, a través de funciones de costos, y eliminar la multicolinealidad presente en el modelo original.

^{Reynès (2019}), presenta una función de producción más flexible y general que la original y la define como función Cobb-Douglas de elasticidad variable, al utilizar elasticidades de producción, que no son necesariamente constantes. Demuestra de esta manera, que se puede generalizar la función sin alterarla por completo, manteniendo la mayoría de sus supuestos vigentes. Dicha modificación se presenta con el objetivo de poder llevar a cabo un análisis profundo, sobre rendimientos crecientes o decrecientes y variaciones en el progreso tecnológico.

A pesar de las limitaciones que posee la función de producción Cobb-Douglas, es importante tomar en cuenta, que representa un rol fundamental en la historia de la economía. Fue la primera ocasión, en la que se estimó una función de producción agregada, a través de un modelo econométrico. Su papel en la evolución de la teoría de la producción y en la del ingreso es de suma importancia, porque rompió con un esquema de investigación teórico, e invitó a los economistas a reforzar sus planteamientos con datos estadísticos. Hoy en día, es la forma más utilizada en los análisis teóricos y empíricos sobre crecimiento y productividad.

Por ejemplo, se continúa utilizando a esta función para hallar el nivel de producción, la elasticidad de los factores productivos y con ello, estimar los niveles óptimos o de eficiencia del factor trabajo, capital, capital-trabajo e insumos en los diferentes sectores de la economía. Es así, que uno de los sectores donde se ha continuado aplicando este análisis ha sido el sector de la manufactura, en países como Yugoslavia y Croacia donde se evidenció que este sector no se encontraba en su nivel óptimo (^{Svarc & Svarc, 1989}). En cambio para el caso de Polonia, se encontró que ha sido aplicada para la industria de acero, se realiza para el periodo 2000-2014, igual que en el caso anterior se utiliza el modelo de Mínimos Cuadrados Ordinarios, el resultado fue que esta industria está creciendo a una tasa menor a la compra y consumo de capital y a la tasa de contratación (^{Gajdzik, 2017}). También se ha utilizado esta función para evaluar la eficiencia de los factores productivos en la industria de remanufactura (^{Saraswati, 2019}).

Otro caso de aplicación ha sido la industria metálica en Indonesia, en este caso se realizaron encuestas a las empresas que están dentro de esta industria, se trata de datos anuales transformados en trimestrales para el periodo 2005-2015. También se utilizaron variables Dummy, para representar los periodos de antes y después de una crisis económica. Después de estos cambios a la función, realizaron una regresión, cuyo resultado fue que, la Industria Metálica es intensiva en capital. También gracias a la variable Dummy, se pudo analizar como la crisis económica del 2008 y 2013, afectaron negativamente a esta industria. Se llegó a la conclusión que, los shocks en esta industria pueden ser detectados y manejados para evitar grandes crisis y así se puede aumentar la resiliencia de la industria, para ello es preciso mejorar su productividad laboral y su inversión tecnológica (^{Jandhana et al., 2018}).

Dentro de los casos de aplicación más interesantes se pueden destacar al sector de la agricultura y de los servicios como el transporte. Resulta muy significativo evidenciar cómo el sector agrícola podría mejorar su eficiencia productiva si se incentiva con políticas públicas esta actividad.

Por ejemplo, para Madagascar es de suma importancia encontrar el nivel de eficiencia de la producción de yuca, debido al alto flujo de dinero, que se da gracias a los bajos costes de producción y a la baja necesidad de materia prima. Después de realizar la regresión y los cálculos necesarios, se llega a la conclusión de que, efectivamente la producción de yuca en Madagascar, no es eficiente, y existe la oportunidad de mejorar, mediante el apoyo del gobierno y que este provea a los granjeros de más tierra y capital (^{Okoye et al., 2016}).

Dentro de la industria agrícola también se encontraron estudios que buscan analizar los factores de crecimiento de este sector aplicado en la provincia de Shanxi. En este análisis, se utilizan datos anuales del periodo 2010-2016, y se resuelve mediante el método de mínimos cuadrados. Después de que el gobierno de la República Popular China reestructuró la industria agrícola, esta provincia observó un crecimiento de manera exponencial, gracias al aumento de inversión y restructuración laboral, se encontró que, el factor más importante para el continuo crecimiento de este sector en esta provincia es la inversión, debido a que el factor trabajo está disminuyendo, ya que un alto porcentaje de la población trabajadora, está migrando a diferentes industrias. Por tal motivo, se debe aumentar la inversión en activos fijos, optimizar la mano de obra existente y aumentar las capacitaciones en recursos humanos (^{Yang et al., 2020}).

Tabla 1:  Síntesis de principales críticas, modificaciones y aplicaciones de la función de producción Cobb-Douglas 

Fuente: Elaboración propia.

A pesar de las limitaciones que posee la función de producción Cobb-Douglas, es importante tomar en cuenta, que representa un rol fundamental en la historia de la economía. Fue la primera ocasión, en la que se estimó una función de producción agregada, a través de un modelo econométrico. Su papel en la evolución de la teoría de la producción y en la del ingreso es de suma importancia, porque rompió con un esquema de investigación teórico, e invitó a los economistas a reforzar sus planteamientos con datos estadísticos. Hoy en día, es la forma más utilizada en los análisis teóricos y empíricos sobre crecimiento y productividad. Seguramente, continuará siendo la base para investigaciones futuras dentro de la comunidad científica, en diversos campos de estudio.

Resultado 2. Datos y metodologías

A lo largo del tiempo la estimación de la función de la producción ha sido un tema ampliamente debatido ya que los autores han tomado diferentes posiciones. Por un lado, los métodos paramétricos que exponen algunas debilidades como la presencia de endogeneidad y simultaneidad en el modelo que los métodos semiparamétricos podrían resolver. Por ejemplo, el método de mínimos cuadrados ordinarios, estima los coeficientes de las variables con un sesgo hacia arriba (endogeneidad de los insumos), el coeficiente del capital, está sesgado hacia abajo (endogeneidad del desgaste) y la presencia de heterogeneidad entre las empresas ya que tienen diferente conocimiento y tecnología. Otro método paramétrico es el estimador de efectos fijos, y el estimador de efectos aleatorios. Por un lado, el estimador de efectos fijos supone exogeneidad estricta en los regresores, supuesto que no se cumple en nuestro caso, adicionalmente si se estima en primera diferencia puede eliminar el efecto fijo. Porque se asume que la heterogeneidad inobservable es invariante en el tiempo, supuesto muy difícil de cumplirse ya que en el tiempo han ocurrido cambio macroeconómico explicados por shocks interno y externos, por otro lado, el estimador de efectos fijos intragrupos supone que la productividad no observada en la función de producción es constante para cada empresa. finalmente, el estimador de efectos aleatorios supone que el efecto inobservable no se correlaciona con las variables explicativas.

De esa manera, autores como Van Biesebroeck (2007), ^{Hassan et al. (2017}), ^{Tsionas y Kumbhakar (2023}), ^{Camino y Bermudez (2021}), proponen estimar la función de producción y posteriormente calcular la productividad utilizando el método desarrollado por ^{Blundell y Bond (2000}) llamado sistema de un modelo generalizado de momentos ya que proporciona una estimación de los parámetros más robusto de entre los métodos paramétricos.

Por otro lado, está el método no paramétrico propuesto por Olley y Pakes en 1996 (citado por ^{Melitz & Polanec, 2015}; ^{Levinsohn & Petrin, 2003}). Con el primero de ellos, asumieron que la inversión se puede utilizar como una variable sustituta de productividad variable en el tiempo. En este sentido, solo se deberían analizar empresas con inversión positiva en los períodos, y presenta dos etapas para la estimación. La primera, se estima mediante métodos semi-paramétricos los coeficientes de los inputs, mientras que, en la segunda etapa, los parámetros del insumo capital pueden ser identificados bajo supuestos sobre la dinámica del proceso de producción. El segundo autor propone el uso de la variable insumos intermedios para representar la productividad no observada (^{Wooldridge, 2009}).

Datos y variables

Las variables utilizadas para la estimación del modelo Cobb-Douglas se dividen en dos tipos: a) variables nivel microeconómico y financiero y b) variables macroeconómicas (tabla 2).

Tabla 2: Variables utilizadas 

Fuente: Elaboración propia.

A nivel microeconómico han habido un sinnúmero de propuestas con estimaciones de datos de panel, donde la variable dependiente es ingresos operacionales, que no incluye ingresos fuera del ciclo o naturaleza del negocio; mientras que las variables independientes son: a) número de trabajadores, b) activo fijo neto, calculado como el activo fijo bruto menos la depreciación acumulada y c) insumos intermedios que incluye gastos de combustibles y lubricantes, servicios básicos, gasto de inventario inicial de materia prima, compras locales y gastos de reparación (^{Camino & Bermúdez, 2021}). Todas las variables son observadas para cada empresa i en el año t. En este sentido, los datos se recolectan de los estados financieros publicados anualmente previo a una depuración de datos eliminando empresas con falta de información. De esta manera se forma un panel no balanceado. Adicionalmente, es necesario mencionar que el modelo puede incluir variables no cuantitativas como la región, provincia, ciudad donde opera la empresa, así como el tamaño de la misma.

Si los datos lo obtenemos a nivel macroeconómico, hay la posibilidad de trabajar con series de tiempo o con datos de corte transversal. La variable dependiente será el valor agregado bruto real del sector o país en análisis, adicionalmente, las variables independientes son: a) la población económicamente activa, b) la formación bruta de capital fijo del sector, industria o país sujetos a análisis. Como lo mencionamos en los apartados anteriores, esta forma de estimar tiene ciertas limitaciones: a) la cantidad o número de observaciones, b) la presencia de endogeneidad, por lo que dificulta la estimación por MCO, y c) la falta de disponibilidad de datos a nivel agregado como el número de trabajadores de una industria y los insumos intermedios.

Entre los estudios más recientes que pretenden estimar la de función producción a través de diferentes metodologías se destacan:

^{Wooldridge (2009}) quien propuso una metodología para estimar la función de producción en su artículo “On estimation firm-level production functions using proxy variables to control to unobservables” cuya especificación econométrica se muestra en la ecuación 12:

Ecuación 12:

Donde

𝑌 𝑖𝑡 = es el logaritmo del Output de las empresas.

𝑊 𝑖𝑡 = Es el vector 1+j del input trabajo.

𝑋 𝑖𝑡 = Es el vector 1 x K del input capital.

Nota: todas las variables expresadas en forma logarítmica.

𝑣 𝑖𝑡 = es la productividad no observada.

𝑒 𝑖𝑡 = es una secuencia de choques que se suponen que son independientes e idénticamente distribuidas.

^{Camino y Bermúdez (2021}) presentaron un análisis de los determinantes de la productividad total de los factores para el sector de la construcción en el Ecuador durante el 2008 al 2019, donde como primer paso estiman la función de producción propuesta por ^{Wooldridge (2009}) para después analizar los factores determinantes de la productividad de los factores de producción, estos determinantes se dividen en cuatro grupos:

A su vez los autores propusieron la siguiente función de producción:

Ecuación 13:

Donde:

𝑤 𝑖𝑡 = Es un choque de correlación serial de la productividad (no observado por el econonometrista, pero observado por las empresas)

𝐾 𝑖𝑗𝑡 = El factor capital.

𝐿 𝑖𝑗𝑡 = El factor trabajo.

𝑀 𝑖𝑗𝑡 = Son los bienes intermedios.

𝜀 𝑖𝑡 = es el error estándar i.i.d (no observado ni precedido por la empresa).

Tomando logaritmos, se tiene:

Ecuación 14:

Donde los parámetros 𝛽,𝛼,𝛾 son las elasticidades del producto con respecto a cada insumo. Adicional, a esta ecuación se incorpora un vector de variable Dummy que hace referencia a: 1) La ciudad a la que pertenece la empresa (Quito, Guayaquil, Cuenca u otros) así como de los subsectores que componen el sector analizado ( 𝜗 𝑖𝑗𝑡 ).

Ecuación 15:

Por tanto, la productividad de todos los factores es definida se con la siguiente expresión:

Ecuación 16:

Al momento de realizar la estimación se considera que el método generalizado de momentos GMM-SYS, es el más adecuado para realizar la estimación de los parámetros de regresión.

Discusión y Conclusiones

El trabajo inicial realizado por ^{Cobb y Douglas (1928}) fue el punto de partida para numerosos debates y críticas planteadas por diferentes estudiosos de la teoría económica. El debate y las críticas el modelo original fueron planteadas en torno a las siguientes circunstancias:

^{Brown (1957}), propone que la función puede lograr un mejor ajuste colocando el tiempo como una tercera variable independiente. ^{Moroney (1967}) afirma que factores como el clima o el desempeño de los factores, no deben estar incluidos en el término de perturbación, sino evidenciados como variables dentro de la función de producción. ^{Antràs (2004}) mencionó que una función de producción agregada es engañosa por lo que sería necesario tomar en cuenta tamaño de la población y los cambios en los salarios, los cuales influyen sobre la oferta de trabajo, y esto influye sobre la variación del factor trabajo, añadiendo que las series de tiempo aplicadas en el modelo original no son estacionarias. ^{Cheng y Han (2014}), proponen añadir variables ficticias en el modelo, por ejemplo, cuando el Estado implementa nuevas políticas o reformas económicas, así como épocas caracterizadas por desastres naturales. Finalmente, ^{Apostolov (2016}), quien sugiere representar al factor capital con la variable Inversión extranjera directa porque es la fuente principal de capital de las empresas.

Lo cierto, es que se continúa aplicando esta función de producción tanto a nivel micro como macro para conocer de mejor manera la producción de una empresa o país. En ese sentido, este análisis contribuye a aproximarse a conocer y medir la productividad de los factores en cada sector de la economía, lo cual es importante para establecer las brechas productivas por sector, tamaño de empresas, regiones y eso contribuye a la toma de decisiones de las empresas y de los hacedores de política pública. Aunque la principal limitación para investigar en este campo es obtener la información de las empresas; sin embargo, la información de la Superintendencia de Compañías y Seguros, si bien no es el universo de empresas puede ser una importante aproximación a conocer la realidad productiva y empresarial del Ecuador.