Introducción

En la actualidad existe un descenso en el desempeño de la matemática por parte de los estudiantes, reflejado en las bajas calificaciones obtenidas en las diferentes pruebas en las que se evalúa dicha materia. El alumnado no toma conciencia de la importancia de la asignatura y los profesores no aplican estrategias creativas para desarrollar el pensamiento lógico matemático de sus estudiantes.

Según la Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (UNESCO, 2020), obtener conocimientos en matemáticas es de suma importancia porque se requiere en muchos ámbitos, ya sea de manera global o en actividades de la vida cotidiana, economía básica e incluso en operaciones de estaciones de tren y aeropuertos. No obstante, la misma fuente manifiesta que es vital demostrar a la sociedad lo imperioso de su necesidad y su conocimiento para aplicarla en la vida diaria.

Por esa razón, cada cierto tiempo, estudiantes de 15 años de varios países son examinados en una prueba llamada PISA que tiene como objetivo obtener información sobre su desempeño en varias asignaturas como Lengua y Literatura en relación con la lectura, Matemáticas y Ciencias, para comparar ese desempeño entre los países sometidos a la prueba. Según el informe PISA de 2018, los puntajes obtenidos con respecto a años anteriores han disminuido considerablemente. La diferencia es de 5 puntos menos que el resultado del año 2015, lo cual genera preocupación porque esto refleja que las habilidades matemáticas obtenidas no son suficientes (Diario El País, 2019).

En Latinoamérica, en el examen PISA, la materia con más déficit fue Matemáticas, en la que se obtuvo un nivel 1, el nivel más bajo, sobre un puntaje de 6. Entre los países con más bajas calificaciones se encuentran Panamá y República Dominicana, cuyos estudiantes obtuvieron un puntaje por debajo del nivel 1, situación preocupante para el sector educativo (Coley, 2020).

En Ecuador, las pruebas como PISA (2017) y Ser Bachiller ODCE-NEVAL (2019) muestran el bajo desempeño de los estudiantes en Matemáticas, pese a los esfuerzos que se realizan (nuevo currículo, libros escolares y tutorías docentes). Es importante que se estudien los aspectos del entorno del estudiante para diseñar estrategias que faciliten el aprendizaje y mejoren las habilidades en la materia (López, 2005).

La presente investigación se realiza con la intención de cumplir con los objetivos planificados en la asignatura de Matemáticas, si bien se acatará lo planteado en el currículo del Bachillerato General Unificado. Su importancia radica en que, con la ayuda de metodología apropiada, el alumno adquiere herramientas para desarrollar el pensamiento matemático aplicando modelos complejos de índole algebraica o funcional. Por lo antes mencionado, se justifica el presente trabajo, que será de gran impacto porque se busca solucionar problemas por medio de la implementación de estrategias creativas que promuevan el aprendizaje del pensamiento matemático.

Así, el objetivo de este estudio fue determinar las estrategias creativas que influyen en el desarrollo del pensamiento matemático en estudiantes de primero de bachillerato del circuito educativo 13D01_C07 de la ciudad de Portoviejo. Adicionalmente, se consideraron como objetivos específicos: identificar las estrategias creativas que utilizan los docentes para potenciar el pensamiento lógico matemático en los estudiantes; y evaluar el nivel de desarrollo del pensamiento matemático que poseen. La hipótesis sería la siguiente: si se aplican estrategias creativas, se desarrollará el pensamiento matemático.

Esta investigación tiene como antecedentes varios trabajos realizados en algunas universidades acerca de la temática estudiada, las cuales se describen a continuación:

^{Baño (2015}) presenta un proyecto con una propuesta innovadora de estrategias didácticas para potenciar el raciocinio en los estudiantes de Educación General Básica Superior empleando argumentos lógicos. Hace uso de una metodología que incluye los métodos: histórico-lógico, analítico-sintético e inductivo-deductivo. De la misma forma, ^{Cunachi (2015}) se basa en la investigación descriptiva-explicativa con los métodos: descriptivo, explicativo e inductivo con el fin de analizar el nivel de razonamiento lógico matemático y determinar las posibles causas.

Zulay (2020), en su investigación, usó un diseño no experimental de campo, de nivel descriptivo bajo la modalidad de un proyecto factible, aplicó encuestas y utilizó el cuestionario como instrumento. Asimismo, consideró la utilización de juegos con dados para afianzar los conocimientos prácticos en temas de adicción, y juegos con cartas en los que se tiene que llevar un puntaje a medida que van avanzando y cada participante debe sumar y comparar el puntaje con los demás compañeros. Además, mencionó que el docente tiene la responsabilidad de que su clase sea dinámica y, al mismo tiempo, tenga la capacidad de lograr en sus estudiantes un aprendizaje significativo.

Medina (2017) describe una estrategia metodológica y didáctica, con base en el constructivismo, donde el estudiante es el constructor de su propio conocimiento. En este sentido, hace énfasis en que la mayoría de las personas tienen dificultades en aprender Matemáticas y que esto se debe a que no cuentan con motivación suficiente y solo cumplen por obligación. Señala también que las metodologías usadas para enseñar se aplican de manera generalizada y no se trata de que los estudiantes lleguen a interactuar entre sí, lo cual sería ideal para intercambiar ideas y formas de pensar.

De los Ángeles (2021), en su trabajo de investigación, realizó una prueba diagnóstica y entrevistó a los docentes usando como métodos la investigación bibliográfica, el método analítico-sintético y el inductivo-deductivo. Resalta que es esencial que los docentes se instruyan sobre estrategias metodológicas innovadoras para el desarrollo de habilidades y competencias que eleven el razonamiento lógico matemático de los estudiantes.

Metodología

La investigación mixta fue realizada en el ámbito cuantitativo y se ajustó al nivel descriptivo, logrando con ello la caracterización del desempeño del estudiantado en las destrezas del pensamiento crítico consideradas en el estudio y teniendo en cuenta los elementos explicadores del pensamiento lógico. En el ámbito cualitativo, se operó a nivel descriptivo, considerando datos emergentes generados a partir de la entrevista en profundidad aplicada al profesorado. Se determinaron algunas estrategias utilizadas y enfoques aplicados para el manejo de la clase con el fin de estimular el pensamiento lógico del estudiantado.

Para la determinación de la muestra de estudio del alumnado se calculó el tamaño de esta a partir de una población conformada por 210 sujetos. De estos, se seleccionaron 137 sujetos matriculados en primer curso del Bachillerato General Unificado del Sistema Nacional de Educación. La muestra no fue equilibrada en relación con factores de género. Sin embargo, la edad es una variable subyacente de la organización interna del sistema, por lo que se contó con sujetos de entre 14 y 16 años. En todos los casos existió un consentimiento informado consignado por los progenitores o representantes legales, de acuerdo con el artículo 8 de la Ley Orgánica de Protección de Datos del Ecuador.

Para la selección de participantes de la muestra de estudiantes se consideró un muestreo aleatorio y probabilístico, basado en la matrícula estudiantil registrada en el Archivo Maestro de Instituciones Educativas (AMIE) y administrado por el Ministerio de Educación del Ecuador. La información sobre los estudiantes fue proporcionada por las instituciones educativas involucradas sin considerar variables como rendimiento o desempeño estudiantil.

Por otro lado, también participaron dos profesores que forman parte del cuerpo docente del circuito 13D01_C07 de la zona 4 del Ministerio de Educación del Ecuador. Estos docentes eran a la vez coordinadores del área de Matemáticas en las instituciones educativas involucradas. En este caso, el muestreo fue intencional, no probabilístico, en función de seleccionar informantes que se ajustaran al perfil requerido para la investigación. Los informantes consignaron, de acuerdo con lo regulado en la normativa vigente, un consentimiento informado para el registro, decodificación, publicación y aseguramiento de la confidencialidad de los datos obtenidos.

Para lograr los objetivos determinados en el estudio se utilizó como instrumento un cuestionario que constaba de 6 dimensiones: seriación, clasificación, identificación, lateralidad, correspondencia y comparación. De acuerdo con Reed (2007), citado por Ramos, Herrera y Ramírez (2010), “las habilidades cognitivas son las destrezas y procesos de la mente necesarios para realizar una tarea, además son las trabajadoras de la mente y facilitadoras del conocimiento al ser las responsables de adquirirlo y recuperarlo para utilizarlo posteriormente” (p. 202).

Cada dimensión se desglosaba en 5 ejercicios graduados para valorar el nivel de madurez de las habilidades intelectuales requeridas para la resolución de problemas en el estadio del pensamiento formal. El cuestionario también se sometió a la prueba Alfa de Cronbach y obtuvo una puntuación global de 0,79, lo que define un adecuado grado de confianza en su estructuración.

Un segundo instrumento fue el utilizado para entrevista en profundidad estructurada en tres dimensiones: a) Identificación del pensamiento lógico; b) Transversalización del pensamiento lógico, y c) Creatividad y lógica. La entrevista constó de 8 preguntas abiertas validadas por dos pares académicos a quienes se les informó de los objetivos del estudio y de las categorías apriorísticas propuestas para la investigación. A partir del criterio de los expertos, se unificaron preguntas y se depuró la intencionalidad de cada una de ellas alcanzando una ponderación promediada de 18/20 desde los criterios de pertinencia, intencionalidad, estructuración y adecuación metodológica.

Para el tratamiento de los datos generados mediante la administración de la batería de pensamiento lógico en etapa formal se recurrió al análisis cuantitativo de nivel descriptivo utilizando el software IBM SPSS v. 25. Una vez recogida la información se depuraron los datos válidos, para lo que se procedió a detectar errores de sintaxis de la migración de la herramienta de recolección de datos y a eliminar los datos duplicados en las respuestas siguiendo la lógica de la investigación.

A partir de la base de datos depurada, se procedió al levantamiento de estadísticas de frecuencias y medias producidas. Luego, se trianguló la información considerando los objetivos específicos del estudio, los referentes conceptuales investigados y los datos obtenidos de las fuentes primarias con las que se evaluaron las dimensiones del pensamiento crítico abordadas en la prueba utilizada y el referente conceptual con el que se valoró la información.

Para el análisis cualitativo se registró en audio la entrevista realizada a los informantes del estudio antes de la consignación de un consentimiento informado. Una vez concluida la entrevista, se borró la información recogida y se sometió a la lectura de sus consignadores. A partir de la aprobación del registro de información se procedió a un análisis inductivo en el que se identificaron las citas más relevantes en cada una de las respuestas, se las codificó y, finalmente, se determinaron las categorías emergentes a partir de las citas obtenidas del texto borrado.

Con los aportes obtenidos en la entrevista se concretaron los resultados mediante un sistema de codificación a partir de los hallazgos y se asignó un código numérico en función de las preguntas formuladas a los informantes. La codificación de los aportes tiene la siguiente estructura: E.1.1. en el que E: instrumento, 1: número de la pregunta del instrumento y 1: participante. Con base en la información obtenida se construyeron los hallazgos que forman parte de los resultados del estudio y que recogen las estrategias y enfoques utilizados por el profesorado para el desarrollo del pensamiento crítico desde la práctica de sus asignaturas.

Resultados y discusión

A continuación, se exponen los resultados de la batería de pensamiento lógico en etapa formal aplicada a los estudiantes de primero de bachillerato del circuito 13D01_CO7. Los datos obtenidos de los instrumentos se analizaron por medio de IBM-SPSS v. 25 aplicando pruebas descriptivas para los datos de la escala autoperceptiva.

Tabla 1 Resultados promedio de la aplicación del test a los estudiantes de primero de bachillerato del distrito 13D01_CO7 

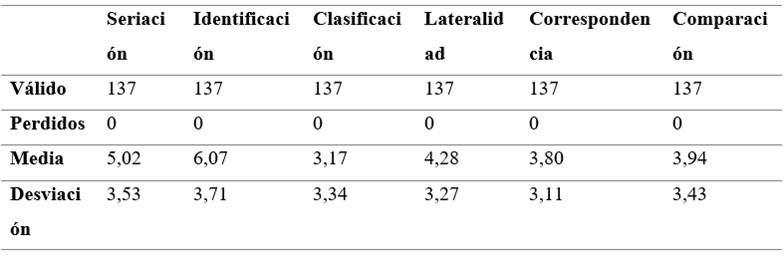
Fuente: Elaboración propia. Nota: Resultados obtenidos mediante la administración de la batería de pensamiento lógico en etapa formal al estudiantado el 16 de febrero de 2022.

En la batería para evaluar el pensamiento lógico en etapa formal para la resolución de problemas matemáticos se comprobó que la dimensión menos consolidada en el grupo de estudiantes fue la clasificación, cuya media estadística se puntuó en 3,17 sobre 10, con una desviación estándar relativamente alta calculada en 3,34 en este caso, según el análisis gráfico. La media más alta corresponde a la dimensión de identificación, con 6,07 puntos sobre 10 y una desviación estándar de 3,71. Por consiguiente, se podría deducir que existen estudiantes con baja consolidación en su pensamiento lógico para la resolución de problemas matemáticos. El profesor debe propiciar innovaciones teóricas o recursos didácticos que estimulen prácticas demostrativas.

Respecto a cómo el docente promueve el desarrollo del pensamiento lógico del estudiantado, la docente entrevistada manifestó que “trato de cumplir con lo planificado y llevar la secuencia de una clase, siguiendo las directrices del Ministerio de Educación” (EP.1. A.1.1), lo cual concuerda cuando argumenta que en Geometría, probabilidad y medidas logra el desarrollo de la lógica en sus estudiantes. “Trato de cumplir con las actividades propuestas en el texto” (EP.1. A.4.1), respuesta que evidencia una metodología tradicional, basada estrictamente en la necesidad de cumplir con lo planificado, sin tomar en cuenta la flexibilidad de currículo, que permitiría utilizar la creatividad en el aula realizando una planificación que lograra en los estudiantes el desarrollo del pensamiento lógico.

En relación con las actividades que propone como docente para promover el desarrollo del pensamiento lógico del estudiantado, la profesora entrevistada afirma que “los trabajos grupales de resolución de los ejercicios buscados de Internet son más fáciles de realizar” (EP.1. A.1.2.); si bien es cierto que una de las actividades que se propone en el aula de clase y, de manera especial, en la asignatura de Matemáticas, es el trabajo grupal. Sin embargo, en muchas ocasiones no se cumple que dentro de ese grupo se generen conocimientos, habilidades y destrezas necesarias para su aprendizaje, debido a que en la mayoría de los casos unos trabajan más que otros. No obstante, quienes trabajan sí logran promover el desarrollo del pensamiento lógico, debido a que con la poca ayuda de sus compañeros, por lo general, siempre cumplen con su trabajo grupal.

Al preguntar sobre las alternativas tecnológicas o recursivas utilizadas para estimular el pensamiento lógico del estudiantado, indica que “no se hace uso de la tecnología” (EP.1. A.2.1), respuesta que refleja una clase tradicional, donde existe una clase magistral dada por el docente y el estudiante es solo un receptor de la información, lo que evidencia una clase monótona que no fomenta en los estudiantes la motivación e interés para aprender la materia.

En lo relativo a la estrategia utilizada por la docente para la resolución de ejercicios, ella indicó: “Explico el procedimiento para la resolución de problemas y después que ellos puedan resolver los ejercicios” (EP.1. A.2.2). De la misma forma, manifiesta que para fortalecer el pensamiento lógico y sus elementos (identificación, seriación, clasificación, lateralidad, comparación, etc.) “trato de evitar los ejercicios de resolución de problemas que vienen en el libro, porque a veces son muy complicados” (EP.1. A.3.1). Al mismo tiempo, dice que “es necesario presentarle problemas que sean fáciles de realizar” (EP.1. C.1.1), respuestas a partir de las que se puede interpretar que se mantiene una metodología inadecuada donde el docente busca la comodidad y el facilismo de los estudiantes, no fomentando en ellos la creatividad ni el pensamiento lógico. Es necesario no subestimar la capacidad de los estudiantes, dado que en ocasiones pueden resolver los problemas difíciles de manera natural, sin ninguna dificultad o con ella, pero resolviéndolos de mejor manera y logrando así desarrollar no solo su pensamiento lógico, sino también su capacidad de ser creativos.

Con respecto a cómo ha logrado la docente el desarrollo de la lógica en sus estudiantes, respondió “que se aprenden fórmulas” (EP.1.A.4.2), lo que demuestra una memorización de contenidos que no aporta nada al aprendizaje. No obstante, en algunas ocasiones se necesita una memorización de ciertas fórmulas, pero es preciso que el estudiante conozca la comprobación de dicha fórmula, de tal manera que no sería memorización, sino más bien un aprendizaje significativo duradero en el tiempo para que pueda ponerlo en práctica cuando sea preciso.

En consideración a la importancia de llevar el pensamiento lógico a otras asignaturas, la entrevistada respondió que “le sirve para otras asignaturas y poder razonar de una manera correcta, ya que deben tener la capacidad de relacionar varios pensamientos y darles una lógica de acuerdo a la asignatura dada” (EP.1.B.1.1). Al mismo tiempo, considera que es importante que “el estudiante sepa obtener la información para luego identificarla, ordenarla, analizarla e interpretarla para darle lógica o solución a un problema” (EP.1.B.2.1). Se puede deducir que la docente acusa la necesidad del desarrollo del pensamiento lógico, no solo en la asignatura de Matemáticas, sino también en otras, pues reconoce la importancia de su desarrollo. Con todo, es necesario fomentarla para que adquiera esa importancia y ponerla en práctica de manera integral.

La problemática evidenciada en las respuestas de la docente se refleja al explicar que “muchas veces no existe una base de años anteriores” (EP.1. C.1.2). Es cierto que este problema existe en todas las unidades educativas, de manera especial en octavo año de la Educación General Básica, y por qué no decir en bachillerato, debido a que el estudiante va arrastrando vacíos de conocimiento que son necesarios para el año siguiente. Esto produce como efecto un bajo rendimiento escolar, además de baja autoestima del estudiante, lo cual desencadena otra problemática en el aula. De igual forma, indicó que “se quedan estancados y no avanzan, toca ayudarles para continuar con la clase” (EP.1. C.2.1). En ocasiones es necesario realizar actividades de refuerzo para nivelar conocimientos y que los estudiantes puedan ir nivelando su aprendizaje con el año que cursan.

Conclusiones

Para obtener mejores resultados en el proceso de enseñanza-aprendizaje es pertinente hacer uso de estrategias encaminadas a conseguirlo. Existe una gran variedad de herramientas de las que el docente puede hacer uso. Por ejemplo, cabe citar la utilización de recursos tecnológicos y la resolución de problemas cotidianos, por medio de los cuales se puede conseguir que el estudiante acceda a una búsqueda de información matemática con rapidez. Además, se pueden plantear actividades de simulación de procesos o situaciones de la realidad, con las que también se promueve la participación por medio de juegos didácticos que contribuyen de forma lúdica a profundizar en el aprendizaje y, asimismo, utilizarse para la evaluación de los resultados del aprendizaje.

Los resultados de la aplicación de la batería de pensamiento lógico en etapa formal constaron de 6 dimensiones y evidenció un promedio aceptable en las dimensiones de identificación y seriación, por lo que tienen correlación entre ellas. Las otras dimensiones evidencian un promedio por debajo de lo aceptable, lo que refleja una inadecuada aplicación de estrategias que desarrollen el pensamiento lógico, manifestado también en la respuesta de la entrevista a la docente respecto a la aplicación de metodología tradicional sin el apoyo de tecnología, escaso desarrollo de la capacidad de resolución de problemas y cumplimiento rígido de la planificación.

La aplicación de estrategias adecuadas por el docente logra desarrollar en los estudiantes el pensamiento lógico, y les ayuda a encontrar soluciones a los problemas que se les presentan. Es así como se logran deducir conclusiones y obtener el conocimiento de forma consciente acerca de cómo se debe actuar y reconocer lo que sucede a su alrededor. Igualmente, también se hallan los orígenes y la lógica existente entre dichas estrategias, las cuales fomentan habilidades que servirán en la vida cotidiana. Para su desarrollo se debe respetar el ritmo de cada estudiante. Por su parte, el docente debe ser creativo y realizar actividades lúdicas, significativas y dotadas de refuerzo para que resulten agradables en el proceso de enseñanza-aprendizaje.