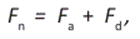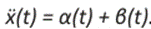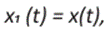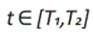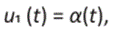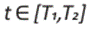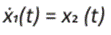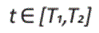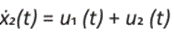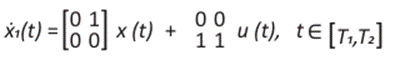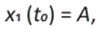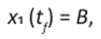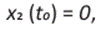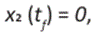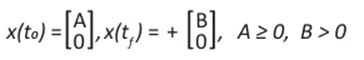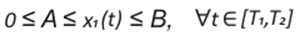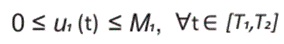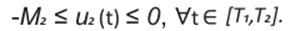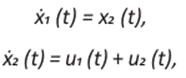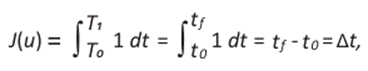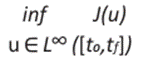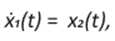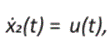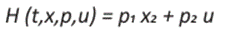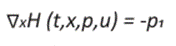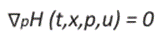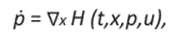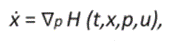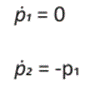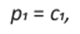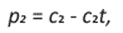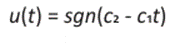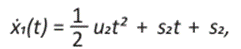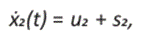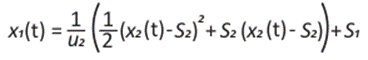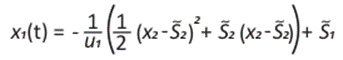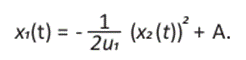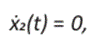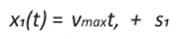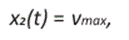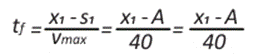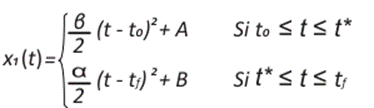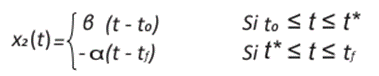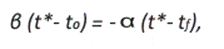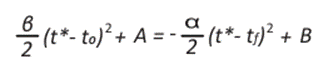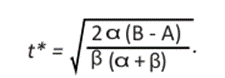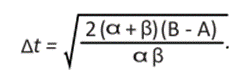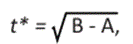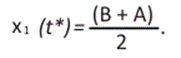INTRODUCCIÓN
El control óptimo, en su esencia, constituye una técnica de modelado matemático diseñada para la óptima gestión de recursos limitados a lo largo del tiempo. Su importancia ha experimentado un notable crecimiento debido, por un lado, a su amplia aplicabilidad en diversas disciplinas, que abarcan desde la economía y las finanzas hasta la ingeniería y la biología. Por otro lado, su relevancia también se extiende al ámbito matemático, donde exige un profundo conocimiento en áreas como el análisis real, el análisis funcional y la teoría de la probabilidad, entre otros.
Inicialmente, esta teoría se basó en los principios de optimización de Pontryagin 3 y Bellman 4; sin embargo, en años recientes, ha experimentado un desarrollo notable, impulsado por desafíos emergentes en campos como la economía matemática y las matemáticas financieras. Específicamente, se enfoca en el estudio de controles y las trayectorias correspondientes que conducen a límites en conjuntos alcanzables, siendo el control de viaje de un vehículo un caso clásico 5-8. En este contexto, la velocidad, registrada por el velocímetro, se retroalimenta y compara con el perfil de velocidad en el control, lo que activa el motor para acelerar en caso de una velocidad demasiado baja o desacelerar en caso de una velocidad excesiva 9.
Por otro lado, la relevancia de este estudio reside en su capacidad para abordar un desafío crucial en el ámbito del transporte público urbano en el Distrito Metropolitano de Quito 10-11. En un mundo enfocado cada vez más en la movilidad sostenible y eficiente, comprender y optimizar los tiempos de viaje en sistemas de trolebuses integrados se convierte en una prioridad apremiante. Nuestra investigación se suma a la creciente literatura en este campo y presenta un enfoque matemático sólido para modelar y analizar estos tiempos de viaje, teniendo en cuenta factores como la velocidad máxima permitida en carriles exclusivos para trolebuses, la distancia entre paradas y la sincronización del sistema de semaforización para garantizar que los vehículos siempre encuentren señales verdes cuando se aproximan.
Este trabajo se relaciona directamente con los artículos 12,13, dado que ambos se adentran en problemáticas relacionadas con el control óptimo y la planificación de trayectorias de vehículos, en los cuales abordan distintos enfoques. El artículo 12 se centra en la gestión de desplazamientos y elevaciones de las catenarias de una grúa, mientras que el trabajo 13 se dedica a analizar el consumo eléctrico de vehículos con motores eléctricos o híbridos. Los resultados obtenidos en estos artículos contribuyen al avance en la comprensión y la resolución de problemas de control de vehículos, lo que complementa y enriquece nuestro enfoque en la mejora del Sistemas Integrado Trolebús.
Los resultados obtenidos no solo son de gran utilidad para planificadores urbanos y autoridades de transporte, sino que también tienen el potencial de mejorar la experiencia de los usuarios del sistema, reducir los tiempos de espera y promover un mayor uso del transporte público. Esto, a su vez, podría contribuir significativamente a la disminución de la congestión vehicular y las emisiones de carbono en áreas urbanas. En resumen, este artículo representa un avance importante en la optimización y mejora de los sistemas de trolebuses integrados, con implicaciones significativas para la movilidad urbana sostenible en la actualidad.
MATERIALES Y MÉTODOS
Metodología.
La investigación se focalizó en el empleo de un modelo de control óptimo, para minimizar el tiempo total de viaje del articulado, consignado a la disminución del tiempo de viaje en cada circuito. El horizonte de optimización se establece como la distancia entre dos puntos geográficos separados por una distancia conocida, en los cuales se impone la velocidad. En la práctica, el horizonte de optimización corresponde normalmente a la distancia entre dos paradas sucesivas, así, la velocidad impuesta es igual a cero. El número mínimo de parámetros posibles para lograr el objetivo de optimización es la velocidad del articulado. Por lo tanto, la salida del control óptimo es la secuencia de valores de velocidad que generaría el tiempo de viaje más bajo, mientras se mueve el articulado entre las dos paradas en un intervalo de tiempo prescrito. La formalización de este problema se puede hacer usando la siguiente descripción y restricciones del sistema que se indican a continuación.
Ecuación dinámica
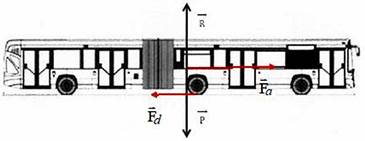
El articulado parte del reposo desde la parada A y es conducido por la vía hasta la parada B donde queda nuevamente en reposo. Por la Segunda Ley de Newton, la fuerza neta F n aplicada al articulado está relacionada con la fuerza F a debida a la aceleración dada al presionar el acelerador y con la fuerza F d provocada por la desaceleración mediante el sistema de frenos, con lo cual se obtiene que:
como la masa del articulado es constante (m > 0) entonces se arriba a la ecuación diferencial
Donde el control α es la aceleración usando el acelerador y β es la desaceleración de frenado.
Una vez escogidas la posición y la velocidad como variables de estado, tenemos el siguiente sistema de ecuaciones diferenciales ordinarias
donde 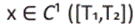 con 0 < T1 < T2 los tiempos entre paradas. Luego, realizando la siguiente identificación para las variables de control admisibles α y β vemos que
con 0 < T1 < T2 los tiempos entre paradas. Luego, realizando la siguiente identificación para las variables de control admisibles α y β vemos que
Resultando así el siguiente sistema de ecuaciones diferenciales: β
cabe notar que las funciones u1 y u2 son continuas a trozos. El sistema formado por (8) y (9) en forma matricial se expresa como
Donde 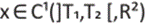 y el vector u es un control admisible y continuo a trozos.
y el vector u es un control admisible y continuo a trozos.
Restricciones físicas
Mostramos que los articulados inician su desplazamiento desde la parada A y se detienen en la parada B. Cuando T1 = t0 indicamos que el articulado abandona la parada A y T2 = t f el tiempo de arribo a la parada B, entonces se sigue que
Adicionalmente, como el articulado parte del reposo (parada A) y se detiene en la parada B, por consiguiente:
Colocando en notación matricial las expresiones (11), (12), (13) y (14) obtenemos las condiciones de frontera:
Asumimos a la vez que el articulado no retrocede, lo cual nos impone las condiciones siguientes:
Teniendo en conocimiento que la aceleración es acotada superiormente por algún límite que depende de la capacidad del motor, y que la máxima desaceleración es limitada por los parámetros del sistema de frenado. Expresamos por M1 > 0 la aceleración máxima y con M2 > 0 a la desaceleración máxima, entonces los controles u1 y u2 satisfacen
Esta formulación utiliza un perfil de referencia, el cual se supone es conocido. La importancia física de limitar la diferencia de velocidad y control (es decir, la aceleración), con respecto a los perfiles de referencia, es garantizar que la solución óptima sigue siendo realista y no produce una velocidad o aceleración incompatible con las condiciones reales.
Modelo de control óptimo
Puesto que existen condiciones terminales tanto en el tiempo final como en la distancia final, se tienen dos enfoques para este problema:
La velocidad y la distancia se consideran como estados del sistema mientras que el tiempo será la variable independiente, de esta forma, se impone que los estados consigan valores predefinidos en el momento final, esto último, se da puesto que representa la longitud entre paradas sucesivas.
Se contempla solamente la velocidad como estado, y tener presente como variable independiente a la distancia; en este caso la restricción de la distancia es espontánea, mientras que la restricción del tiempo debe ser efectuada por separado.
En esta investigación se trabajó con el primer enfoque, a causa de que los métodos numéricos para esta orientación tienen una implementación sencilla. Por otro lado, el segundo enfoque, al contrario, es más propicio en ese sentido y representa la opción preferida, pero los métodos numéricos para la implementación son mucho más avanzados y requieren de herramientas matemáticas más potentes.
Subsiguientemente, mostramos el problema de control óptimo asociado al estudio del fenómeno de los tiempos de viaje del articulado. Vamos a considerar el vector de estados 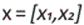 (posición y velocidad). Tomamos en cuenta el sistema de ecuaciones (8)-(9)
(posición y velocidad). Tomamos en cuenta el sistema de ecuaciones (8)-(9)
sujeto a las condiciones (16), (17), (18) y (19). Este problema está asociado a la función de coste J definida por:
donde (20) representa el tiempo entre paradas consecutivas. El valor de t f representa el tiempo al momento de completar el segmento de la vía que hay entre las paradas A y B y t0 representa el tiempo con el cual parte el articulado de la parada A.
El problema de control óptimo se escribe:
Encontrar una función 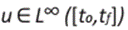 tal que la trayectoria
tal que la trayectoria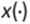 asociada al sistema (8)-(9) minimice J
asociada al sistema (8)-(9) minimice J
Esto significa que cualquiera que sea 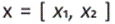 (posición y velocidad objetivos en Δt), hay un control
(posición y velocidad objetivos en Δt), hay un control 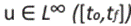 que lleva el articulado de la parada A hacia la parada B en el tiempo Δt14,15.
que lleva el articulado de la parada A hacia la parada B en el tiempo Δt14,15.
Existencia y unicidad
Para mostrar que existe la función u tal que minimice a la función de coste J se debe probar que el problema
tiene una solución única 15). Para esto, partimos de una condición inicial 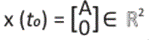 y se desea arribar al objetivo
y se desea arribar al objetivo 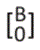 en un tiempo mínimo.
en un tiempo mínimo.
Consideraremos un sistema más simple con las mismas funcionalidades
con 0 ≤ u1 ≤ M2 y -M2 ≤ u2 ≤ 0 y con la restricción de velocidad |x2| ≤ vmax donde vmax = 40 km/h.
El Hamiltoniano 16,17-19
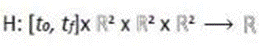 asociado al sistema de control lineal (22)- (23) se expresa como
asociado al sistema de control lineal (22)- (23) se expresa como
Un cálculo elemental sobre las derivadas parciales del hamiltoniano muestra que
Se toma en cuenta que dado que el vector adjunto p = (p1, p2) no debe ser trivial, p2 no puede desaparecer en un intervalo, de lo contrario, también tendríamos p1 = -ó2 = 0. Aplicando el Principio de Máximo de Pontryagin 20,5, vemos que
Juntando las expresiones en (25), (26), (27), (28) obtenemos
de donde se desprende
deducimos que, en casi todas partes,
con sgn(x) la función signo de x . Esas condiciones imponen dos tipos de órbitas. Entonces para u = u2
de donde se desprende que
Análogamente para u = -u1
Ahora con las condiciones iniciales x1(t0) = A, x2 (t0) = 0, obtenemos S1 = A, S2 = 0
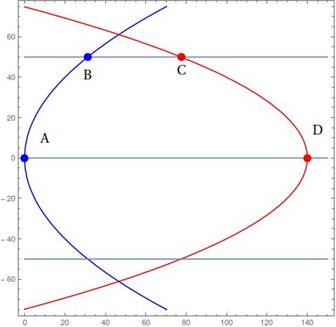
Y así las trayectorias son por lo tanto parábolas de eje x, recorridas en la dirección creciente de x2. Mientras que para el caso u = -u1; las trayectorias son, por tanto, parábolas de eje -x, recorridas en la dirección decreciente de x2.
Estas parábolas se muestran en la Figura 2. En azul tenemos las trayectorias de aceleración (u = β) y en rojo las de ruptura (u = - α). La restricción a la velocidad se logra en B desde A.
Se debe tener en cuenta que el control óptimo se escribe como una función de retroalimentación del estado ya que tenemos
u = β si x está por debajo de la curva de conmutación en este caso, es necesario acelerar.
u = α si x está por encima de esta curva en este caso, es necesario desacelerar.
De B a C tenemos el sistema
Lo que da
por lo que la trayectoria de tiempo mínimo de A a D es A → B → C → D. A partir de esos datos podemos calcular fácilmente tf y así:
A partir de la ecuación (29) se obtiene la solución, en función de t, para la ecuación
donde se observa que el cambio de velocidad tiene lugar en el momento t* (switching time). Tanto la distancia, x1 y la velocidad en, x2, son continuas en t = t*, se debe tener que
Al despejar t* de las ecuaciones (42) y (43) tenemos que el switching time21 viene dado por
y del cual se desprende que el tiempo óptimo ∆t es
Así vemos que el problema está determinado y el control óptimo está descrito por (29) la cual presenta una discontinuidad en t = t* y solamente toma sus valores máximos, β , y mínimo, α. A este tipo de control se lo denomina bang-bang y se caracteriza por tomar valores iguales a uno, es decir, α = β = 1 . Por ende, el switching time y el desplazamiento x1 en t* se expresan como sigue
Donde la ecuación (47) indica que la máxima velocidad se alcanza en el punto intermedio entre paradas contiguas, dado que la aceleración máxima se aplica desde el principio y se invierte en el punto medio. Esto supone, por supuesto, que no hay fricción ni velocidad terminal que se pueda lograr a lo largo del camino.
Preparación del código
Se realizó la programación de un script con una codificación destinada a establecer los perfiles de desplazamiento, velocidad y aceleración óptimos, tomando en cuenta la documentación de la librería GEKKO y la teoría de control óptimo asociada a este tipo de modelos 1.
Implementación del modelo
Con este modelo de control de tiempo óptimo, se realizó las simulaciones para el perfil de velocidad, aceleración y desplazamiento entre dos paradas consecutivas A y B que distan en 400m 2 y considerando que la velocidad máxima permitida para un articulado del trolebús es de 40km/h; a su vez se consideró que el articulado avanza en un intervalo de tiempo 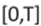 , con T ≈ 108 seg representando el tiempo total al recorrer las 75 paradas del trolebús. Con estos datos procesados se obtuvieron 4 gráficas:
, con T ≈ 108 seg representando el tiempo total al recorrer las 75 paradas del trolebús. Con estos datos procesados se obtuvieron 4 gráficas:
RESULTADOS
Los resultados se presentan en tablas y gráficas, que detallan la información de la variable espacial con valores de las distancias entre paradas consecutivas y, además, contiene la información de la variable temporal con valores entre 0 y T > 0 .
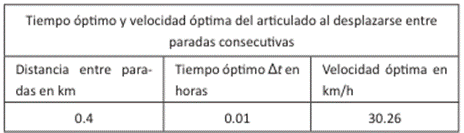
En la Tabla 1 notamos los valores del tiempo óptimo y velocidad óptima durante el trayecto entre la parada A y la parada B, calculados con el lenguaje de programación Python, en particular, el paquete GEKKO 22.
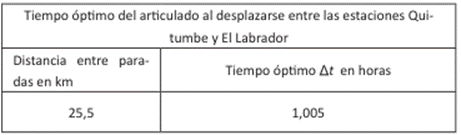
En la Tabla 2 notamos los valores del tiempo óptimo durante el trayecto entre la parada Estación de Quitumbe y la Estación El Labrador.
Tabla 2 Valores del tiempo óptimo ∆t y de la velocidad óptima para todo el Sistema Integrado Trolebús
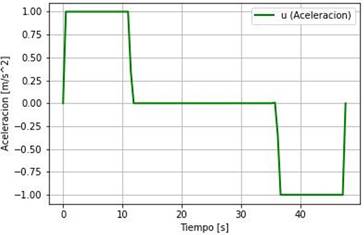
En la Figura 3 notamos que la aceleración del articulado se comporta como un control bang-bang, donde el articulado mantiene una aceleración constante de 1m/s2 hasta el punto de switching, para luego disminuir la aceleración, debido al sistema de frenado, a un valor constante de 1m/s2.
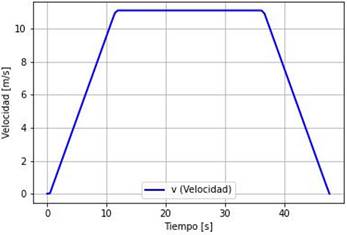
En la Figura 4 observamos que la velocidad del articulado parte del reposo al tiempo t0 = O s y esta va aumentando de forma constante en los primeros durante hasta alcanzar la velocidad máxima permitida de 11,11 m/s = 40km/h la cual se mantiene constante durante los 15 s siguientes, para luego disminuir su velocidad hasta llegar con velocidad cero en el tiempo tf = 48 s.
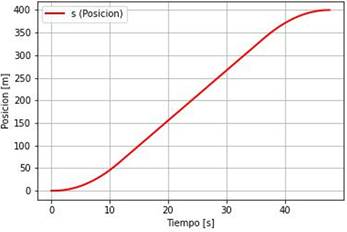
En la Figura 5 se muestra la posición del articulado respecto al tiempo, esta gráfica permitirá identificar que la trayectoria es una función creciente sin presentar alteraciones durante el trayecto entre las paradas A y B.
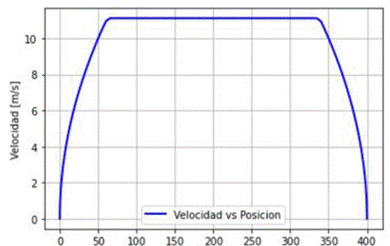
En suma, la Figura 6 pone en manifiesto el perfil de velocidad óptimo que el articulado deberá seguir durante el trayecto entre dos paradas consecutivas. Se percibe que el articulado parte de la parada A con una velocidad igual a cero y conforme avanza durante los primeros 100 metros, aumenta paulatinamente la velocidad hasta alcanzar la velocidad máxima permitida 11,11 m/s = 40km/h para mantenerla durante 300 metros y luego disminuirla suavemente para llegar con velocidad cero a la parada B
DISCUSIÓN
El presente trabajo tiene como finalidad mostrar que la teoría de Control Óptimo puede ayudar a los problemas de movilidad de pasajeros del Sistema Integrado Trolebús, lo cual se logra explicar con los resultados presentados, además se recalca que existen variables que no fueron consideradas en el modelo como es el caso de la velocidad del viento, fricción, tipo de vía, número de semáforos 20,21, por ende, estas simplificaciones permitieron tener un modelo sintético que permite un análisis más flexible. También, esta simplificación podría desvirtuar los resultados.
El estudio nos permite demostrar el efecto de controlar la velocidad del articulado durante todo su trayecto, lo cual motiva a profundizar su estudio y a generar escenarios que permitan desarrollar mejores planificaciones en cuestiones de movilidad, más aún, a valorar la importancia de la modelización matemática en temas de movilización.
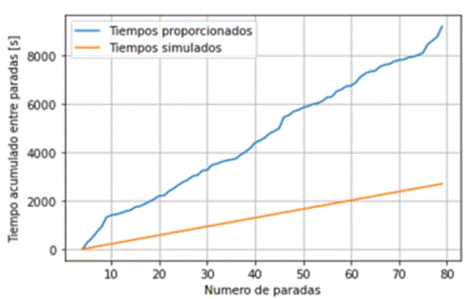
A partir de la Tabla 2 se evidencia que el tiempo óptimo del articulado al desplazarse entre las estaciones Quitumbe y El Labrador es menor al tiempo de viaje registrado por la Empresa Pública Metropolitana de Transporte de Pasajeros de Quito (EPMTPQ), además, cuando se hace el recorrido por las 76 paradas y se examina los tiempos de viaje entre ellas, se obtiene un tiempo total 2,56 horas. Por consiguiente, al unir estos 76 datos, uno a continuación de otro, se obtiene una gráfica del tiempo, como se observa en la Figura 7.
A su vez, se evidencia que las gráficas del tiempo acumulado presentan una tendencia lineal creciente, destacando que la recta obtenida con el modelo está por debajo de la gráfica de los datos proporcionados, ratificando así que los resultados obtenidos con el modelo son bastante aceptables.
Por otra parte, los tiempos óptimos se obtuvieron a través de la resolución del problema de tiempo óptimo, que en el presente trabajo muestra una disminución del 39 % en el tiempo total de viaje, porcentaje considerable que surge de la información en la Tabla 2, y confirma el buen ajuste del modelo y su significativa predicción del tiempo óptimo.
En el ámbito de la investigación relacionada con simulaciones de control óptimo de tiempo mínimo, destacan varios estudios relevantes llevados a cabo por investigadores como Dal Bianco, Lot y Gadola 23, Cots 13, Saccon 24, Pickhardt 9, y Li, Wang y Shao 25. Estos trabajos se centran en la aplicación de simulaciones de tiempo mínimo en escenarios que involucran vehículos siguiendo trayectorias predefinidas y abordan aspectos detallados del modelo, que incluyen la dinámica completa del chasis, los movimientos de la suspensión, las maniobras de las ruedas, el consumo de energía eléctrica, así como los movimientos simultáneos de desplazamiento y elevación de las catenarias.
Es importante destacar que el estudio de Li, Wang y Shao 25 se concentra en vehículos articulados utilizados para el transporte de carga, los cuales deben navegar por carreteras sinuosas o congestionadas con el objetivo de llegar a una posición objetivo en el menor tiempo posible, mientras cumplen con restricciones de aceleraciones laterales y longitudinales para evitar el fenómeno conocido como el efecto tijera. Estos trabajos proporcionan una visión detallada de la complejidad intrínseca que implica la formulación de un modelo de control óptimo cuando se consideran múltiples variables y restricciones. En resumen, estas investigaciones son fundamentales para comprender y abordar los desafíos relacionados con el control óptimo en contextos de tiempo mínimo, lo que tiene aplicaciones significativas en una amplia gama de campos, desde la ingeniería de vehículos hasta la movilidad eléctrica y la planificación de rutas en entornos complicados.
V. CONCLUSIONES
Este estudio ha proporcionado una comprensión profunda del comportamiento de los articulados en el sistema Trolebús del Distrito Metropolitano de Quito. Además, hemos logrado obtener el perfil de velocidad óptima en la ruta analizada, lo que sienta las bases para la formulación de estrategias a corto, mediano y largo plazo. Estas estrategias tienen el potencial de reducir la congestión vehicular y mejorar significativamente la movilización de pasajeros en el Distrito Metropolitano de Quito.
Un hallazgo importante es que los tiempos registrados por la Empresa Pública Metropolitana de Transporte de Pasajeros de Quito son mayores que los tiempos obtenidos a través de nuestro modelo de control de tiempo óptimo. Esto indica que nuestro modelo puede ofrecer estimaciones más precisas de los tiempos de viaje óptimos en la Troncal Central Trolebús. Esta información será invaluable para prever y abordar los desafíos causados por la falta de planificación y organización en el sistema de transporte.
En la actualidad, existen diversos modelos matemáticos basados en ecuaciones físicas que pueden integrar factores como velocidad, aceleración y fricción en el movimiento de los articulados durante su recorrido. El estudio proporciona una base sólida para la toma de decisiones en la planificación y gestión del sistema de transporte público en el Distrito Metropolitano de Quito, con el potencial de mejorar la eficiencia y la calidad del servicio ofrecido a los pasajeros, al tiempo que contribuye al avance de la ciencia y la planificación urbana en general