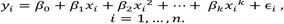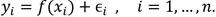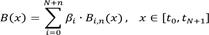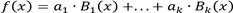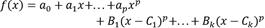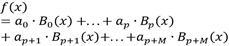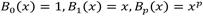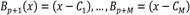INTRODUCCIÓN
Los accidentes de tránsito representan un problema que atenta contra la salud de las personas, los principales factores que inciden en la ocurrencia de este tipo de acontecimientos son entre otros la impericia de los conductores y las condiciones de las vías 1.
Ante tal situación los fabricantes de automotores y de autobuses no pueden intervenir directamente, sin embargo, están en capacidad de minimizar la afectación de los accidentes en las personas involucradas, a través de la fabricación de componentes que brinden buena resistencia al impacto y a la deformación.
Esto constituye un aspecto inherente a la ingeniería mecánica automotriz, siendo que en el diseño de los vehículos se consideran aspectos como la forma y los materiales de los componentes automotrices 2.
Bajo el contexto indicado, los fabricantes de vehículos y de autobuses suelen implementar herramientas tecnológicas para el análisis estático y dinámico de las colisiones y choques.
La simulación de impacto es una de las herramientas indispensables, que consiste en la utilización de un software de Elementos de Análisis Computarizado (CAE) para representar un choque real. De este modo se conoce el efecto que las cargas de impacto provocan en las estructuras de los automotores (estados de tensiones y deformaciones) 3.
En el análisis estático y dinámico de una colisión de vehículos o de un choque intervienen las magnitudes físicas, tales como: velocidad lineal, fuerza, esfuerzo, tiempo de impacto, factor de seguridad de diseño (FDS), entre otras. El FDS es el cociente calculado entre el esfuerzo de cedencia de un material y el esfuerzo dado por las condiciones a las que está sometido el diseño 4.
De entre las magnitudes señaladas, la velocidad de circulación de los vehículos es la que condiciona el comportamiento del fenómeno, pues no se experimenta el mismo resultado en un siniestro de tránsito a distintas velocidades 5. En este sentido, el presente estudio considera el análisis del efecto que produce la velocidad de circulación de un automóvil en las magnitudes fuerza de impacto, tiempo de duración del impacto, deformación y factor de seguridad (FDS) durante un evento de choque contra la parte posterior de la carrocería de un autobús.
El trabajo se enfoca en la caracterización de los modelos teóricos estadísticos de regresión paramétricos polinomiales y no paramétricos B-splines. Los primeros son tradicionalmente conocidos y relativamente sencillos de utilizar, sin embargo, conllevan algunas restricciones para ser utilizados en cada caso particular 6.
Adicionalmente es necesario considerar la bondad de ajuste de los modelos, para tomar una decisión respecto al que se adapta de mejor manera a las condiciones de los problemas estudiados 7. El impacto de la investigación radica en el suministro de información útil para el desarrollo de tecnologías en la fabricación de carrocerías de autobuses.
Modelos de regresión paramétricos polinomiales.
La regresión polinomial es un caso especial de regresión múltiple, con solo una variable regresora o predictora X. El modelo de regresión polinomial de una variable explicativa o regresora se puede expresar de la siguiente manera:
Donde:
n es el número de datos disponibles a ser utilizados para hallar el modelo.
k es el grado del polinomio 8.
Métricas de medición del error y bondad de ajuste.
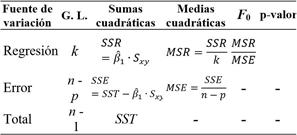
Para la evaluación de un modelo de regresión se obtiene la tabla ANOVA a partir de los parámetros de la variación: regresión, error y total, como se muestra en la Tabla 1:
F0, es el estadístico de prueba F de Snedecor.
MSR, media cuadrática de la regresión.
MSE, media cuadrática del error.
SSR, suma de cuadrados de la regresión.
SSE, suma de cuadrados del error.
n, es el número de datos disponibles a ser
utilizados para hallar el modelo.
k, es el grado del polinomio.
p = k+1.
La bondad de ajuste de un modelo de regresión es el principal criterio que valora su capacidad de predicción de una variable respuesta. Para el efecto se mide la variabilidad explicada por el modelo sobre la variable a predecir y la forma de hacerlo es a través del uso del error estándar de los residuos (RSE), el test F de bondad de ajuste mostrado en la tabla ANOVA y el coeficiente de determinación ajustado R2 ajustado 10.
Modelos de regresión no paramétricos B-splines.
Los modelos de regresión no paramétricos permiten una estimación flexible de efectos no lineales y no requieren ningún supuesto restrictivo con respecto a una determinada forma funcional paramétrica.
En el caso de una sola covariable continua x, el modelo estándar para la regresión no paramétrica se define de la siguiente manera:
Para la variable de error Єi, se supone que la función f presenta ciertas características de suavidad, como continuidad o diferenciabilidad, pero no se especifica una forma paramétrica específica. Una spline es una función que se construye por partes a partir de funciones polinomiales, el término proviene del “listón elástico” 11. Los splines “son curvas polinómicas por trozos continuamente diferenciables hasta un orden prescrito” 12. Entre los ejemplos más característicos se tienen C0, una spline lineal por trozos y C1 un spline cúbico.
Función base B-spline
Una función B-spline es la función de base interpolativa de máxima diferenciación y representa una generalización de la curva de Bézier. Los B-splines se definen por su orden m y el número de nodos interiores N (hay dos puntos finales que son en sí mismos nodos, por lo que el Número total de nodos será N + 2). El grado del polinomio B-spline será el orden de spline m-1 (13).
Una B-spline de grado n (de orden spline m = n+1) es una curva paramétrica compuesta de una combinación lineal de B-splines de base Bi,n (x) de grado n dada por:
La función f tiene la siguiente estructura:
Donde:
k, número de bases.
a1, …, ak, parámetros desconocidos.
B1,…, Bk, funciones polinomiales de base B-spline.
βi, puntos de control o puntos de Boor.
La secuencia t se conoce como una secuencia de nodos, siendo un nodo el término individual de la secuencia (13).
La regresión basada en B-spline de orden p se considera de la estructura:
Donde:
a0, …, ap y B1, …, Bk, coeficientes a determinar.
El spline f puede ser expresado como una combinación lineal de la forma:
Las funciones mostradas a continuación constituyen una base de funciones polinómicas del spline:
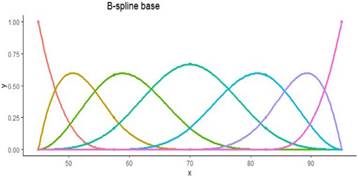
En la Figura 1 se muestran las curvas B-spline de base para un determinado grado del polinomio, número de vértices del polígono de control y nodos internos.
MATERIALES Y MÉTODOS
Materiales
Para el desarrollo de la investigación se hace uso de los siguientes materiales:
Software estadístico R 14.
Software CAD-CAE.
Computador y equipos de oficina
Metodología
La investigación es de tipo correlacional bivariada, siendo las variables de interés: velocidad lineal del automóvil, fuerza, factor de seguridad (FDS), tiempo de impacto y deformación. El diseño de la investigación es no experimental de corte transversal, porque los datos fueron obtenidos en las condiciones regulares de ocurrencia de los eventos y fueron analizados en una sola oportunidad para obtener modelos de regresión.
De acuerdo al enfoque, la investigación es de tipo cuantitativa, la información corresponde a datos numéricos que permiten establecer relaciones existentes entre las variables. Según la modalidad, la investigación es bibliográfica y de campo. En cuanto a la obtención de los datos de la simulación de impacto vehicular se lo realizó mediante el uso de un software CAD-CAE.
Muestra y variables.
La muestra corresponde a los datos disponibles de las variables involucradas, conforme indica la Tabla 2:
Recolección de información.
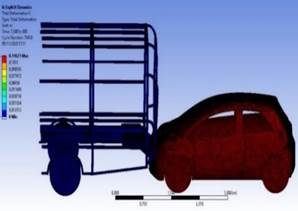
Los datos de las variables de la Tabla 2 se generaron en un software CAD-CAE a partir de la simulación del choque de un automóvil contra la parte trasera de la carrocería de un autobús a diferentes velocidades del auto pequeño.
Los valores obtenidos fueron particulares para las condiciones del problema (materiales de automotores y velocidades a las que se producen los impactos). La estructura del autobús fue diseñada con una sección tubular cuadrada de acero galvanizado con dimensiones de 40 mm de largo y 3 mm de espesor.
A continuación, en la Figura 2 se presenta una captura de pantalla de la simulación realizada:
Procesamiento de la información y análisis.
Tipos de datos
Los datos son de tipo numérico discreto o numérico continuo. Se aclara que la velocidad de desplazamiento del auto, se considera como una variable numérica discreta y no continua, dado que se planteó una situación en la que se simularon impactos a diferentes velocidades de choque, con incrementos de una unidad dentro del rango 45 a 95 km/h.
Depuración y limpieza de los datos
Se efectuó una clasificación, depuración y limpieza de los datos, mediante utilización de una hoja de cálculo y el software R.
Preparación del código
Se realizó la programación de un script con una codificación que establece los modelos de regresión polinomial y B-splines, tomando en cuenta el lenguaje de código correspondiente y la teoría estadística inherente a los modelos.
Generación del modelo
Se determinaron los modelos de regresión polinomial y B-splines que se ajustaron a los datos disponibles en cada caso mediante el software R (15). Para comparar la bondad de ajuste de los dos modelos obtenidos para cada relación se efectuaron las siguientes actividades:
Aplicación de la prueba de Wilcoxon para identificar si existen diferencias significativas entre ambos modelos (polinomial y B-splines), con un nivel de significancia de 0.05.
Generación de un gráfico Q-Q Plot para identificar las diferencias entre los intervalos de confianza de ambos modelos y corroborar los resultados de la prueba de Wilcoxon 16.
Elaboración de los diagramas de cajas de la variabilidad de la longitud del intervalo de confianza de los dos modelos.
Construcción de los dos gráficos (modelo polinomial y B-spline) de la dispersión de puntos, curvas e intervalos de confianza en una gráfica.
Decisión del modelo más idóneo para expresar la relación entre las variables. Para determinar el grado de la regresión polinomial se aplicó la prueba de diferencias significativas ANOVA entre modelos de distinto grado, priorizando por simplicidad el modelo de menor grado entre aquellos que no tienen diferencias significativas. Por su parte, en cuanto a los modelos de regresión no paramétricos B-splines, se evaluó la bondad de ajuste mediante el criterio de información de Deviance (DIC) 17 y el criterio de información de Akaike (AIC) 18.
Declaración de la aceptación o rechazo de los modelos de regresión obtenidos, con base en las pruebas de hipótesis de validación de los modelos.
Supuestos del modelo de regresión paramétrico polinomial
Los supuestos verificados para los modelos de regresión paramétricos polinomiales fueron:
Número de observaciones n es mucho mayor que el de parámetros β.
Homocedasticidad, que implica que la esperanza matemática del error sea 0. E(Î)=0 con varianza constante, a través de aplicar la prueba de Breusch-Pagan estudiantilizada 19.
Residuos del modelo no están correlacionados entre sí, mediante la prueba de Durbin-Watson 20.
Pruebas de hipótesis de validación de los modelos .
Para la determinación de la validez y la bondad de ajuste de los modelos de regresión se aplicaron las siguientes pruebas de hipótesis:
Prueba de rechazo de la nulidad de los parámetros β´s de cada modelo polinomial y de los coeficientes del modelo B-spline, mediante el estadístico t de Student: H0: β1=β2=...=βk=0; H1:βj≠0 para al menos un j.
Prueba de diferencias significativas para la validez de los modelos, mediante la prueba F de Snedecor presentada en la tabla ANOVA: F>F(α,p-1,n-p).
Pruebas de Shapiro-Wilk y Kolmogorov- Smirnov corregida por Lilliefors para comprobar la distribución normal de los residuos de los modelos de regresión Î~N(μ,σ2) 21) (22) (23.
Pruebas de Durbin-Watson para la independencia de las variables (no autocorrelación) y prueba de homocedasticidad de Breusch-Pagan.
Se omite un estudio de colinealidad puesto que todos los modelos tienen una sola variable explicativa
RESULTADOS
Los resultados se presentan en tablas que detallan la información de las variables explicativas y regresoras, número de datos procesados, tipo de modelo de regresión, grado del polinomio, número de vértices del polígono de control (modelo B-spline), intercepto y coeficientes del modelo, prueba de hipótesis F, p-valor, RSE, R2 ajustado, MSE, SSE, RSME, SST; pruebas de normalidad de residuos, residuos no correlacionados, homocedasticidad de residuos, diferencias entre modelos, y códigos de significancia.
Todas las tablas se subdividen verticalmente en dos partes, una para el modelo de regresión polinomial y otra para el B-spline, a fin de comparar las características de ambos modelos e identificar la bondad de ajuste respectiva.
Velocidad vs Fuerza
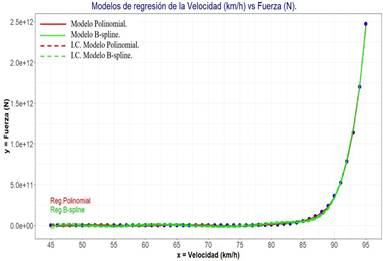
En la Figura 3 se muestra la gráfica de dispersión de puntos de la velocidad versus la fuerza de impacto, conjuntamente con las curvas de los dos modelos de regresión y las líneas de los intervalos de confianza al 95%:
En la Tabla 3 se presentan los modelos de regresión polinomial y B-spline de la variable velocidad versus la fuerza:
Tabla 3 Modelos de regresión de la velocidad y fuerza
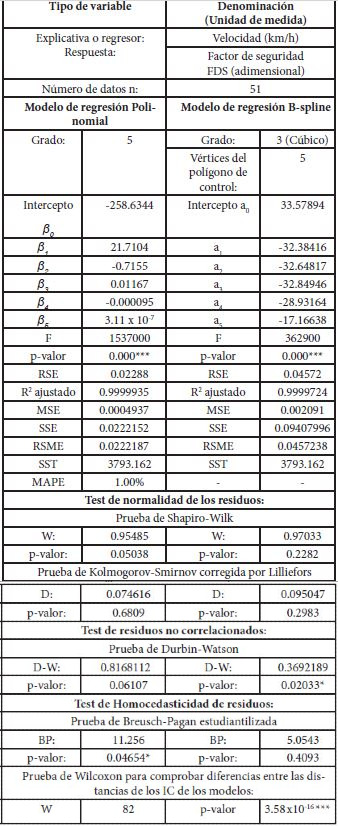
Códigos de significancia: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
La distribución de los puntos sigue una curva en forma de parábola creciente; conforme se incrementa la velocidad del auto, la fuerza del impacto se eleva ostensiblemente, por ello la variable respuesta está en escala logarítmica. Ambos modelos son válidos y presentan intervalos de confianza estrechos, no obstante, el modelo de regresión polinomial es el que ofrece una mejor bondad de ajuste, ya que los residuos son menores que los del modelo B-spline. Es decir que la relación de la variable velocidad y la variable fuerza con las condiciones dadas del problema se expresa mejor mediante la regresión paramétrica polinomial de grado 8.
Velocidad vs FDS
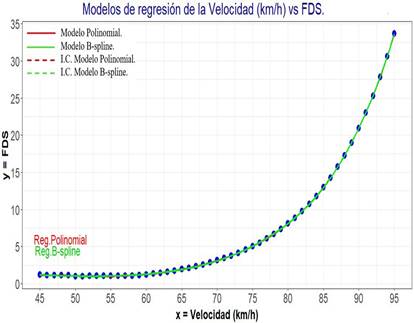
En la Figura 4 se muestra la gráfica de dispersión de puntos de la velocidad versus el FDS, conjuntamente con las curvas de los dos modelos de regresión y las líneas de los intervalos de confianza al 95%:
En la Tabla 4 se presentan los modelos de regresión polinomial y B-spline de la variable velocidad en km/h versus la variable FDS:
La distribución de los puntos sigue una curvaenforma de parábola creciente, conforme se incrementa la velocidad de movimiento del auto, el FDS de diseño requerido también crece. Comparativamente cuando la velocidad de desplazamiento del vehículo que impacta a la carrocería del autobús no excede de 60 km/h, el FDS de diseño aproximadamente no supera el valor de 2, pero a medida que se eleva la velocidad el FDS requerido para que la estructura no se deforme está en torno a 35. Ambos modelos son válidos y tienen intervalos de confianza estrechos, no obstante, el modelo de regresión polinomial es el que ofrece una mejor bondad de ajuste, ya que los residuos son menores que los del modelo B-spline.
Es decir que la relación de la variable velocidad y la variable FDS con las condiciones dadas del problema se expresa de mejor manera con el uso de la regresión paramétrica polinomial de grado 5.
Velocidad vs Tiempo de impacto
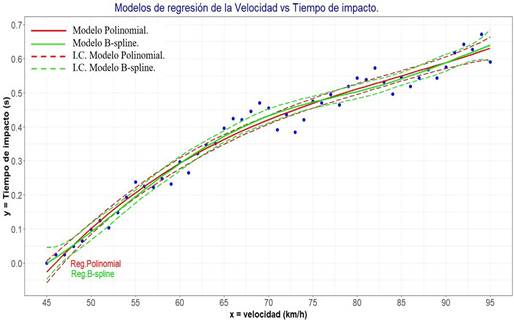
En la Figura 5 se presenta la gráfica de dispersión de puntos de la velocidad versus el tiempo de impacto, conjuntamente con las curvas de los dos modelos de regresión y las líneas de los intervalos de confianza al 95%:
En la Tabla 5 se presentan los modelos de regresión polinomial y B-spline de la variable velocidad en km/h versus el tiempo de impacto en segundos:
Tabla 5 Modelos de regresión de la velocidad y tiempo de impacto.
Códigos de significancia: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
La distribución de los puntos sigue una curva con forma parecida a una función logarítmica.
Conforme se incrementa la velocidad de movimiento del auto también aumenta el tiempo de duración del impacto, aunque el ritmo de crecimiento va disminuyendo a medida que la velocidad se acerca a la máxima del ensayo de 95 km/h. Ambos modelos ofrecen una aceptable bondad de ajuste, aunque con intervalos de confianza que dejan por fuera a algunos puntos.
Los dos modelos son válidos, pero el modelo de regresión B-spline es el que ofrece una mejor bondad de ajuste, ya que los residuos son menores que los del modelo polinomial. Es decir que la relación de la velocidad y tiempo de duración del impacto con las condiciones dadas se expresa mejor a través de una regresión no paramétrica B-spline de grado 3.
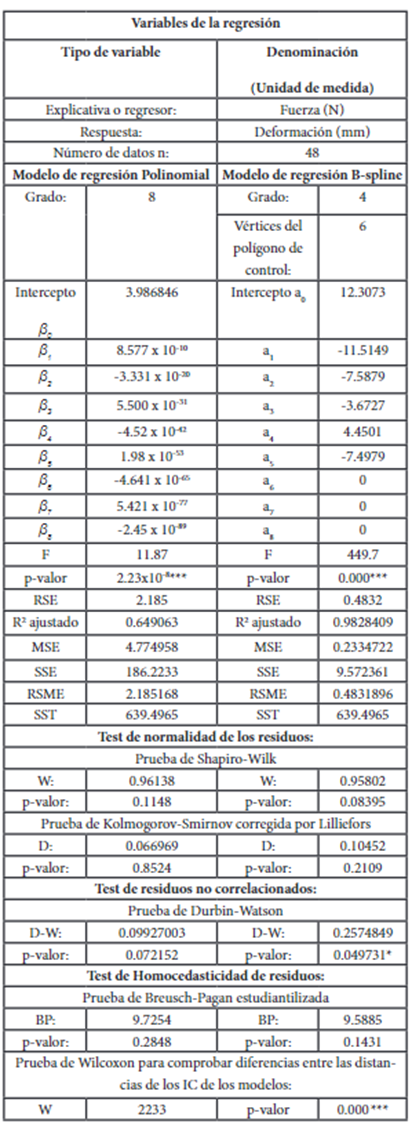
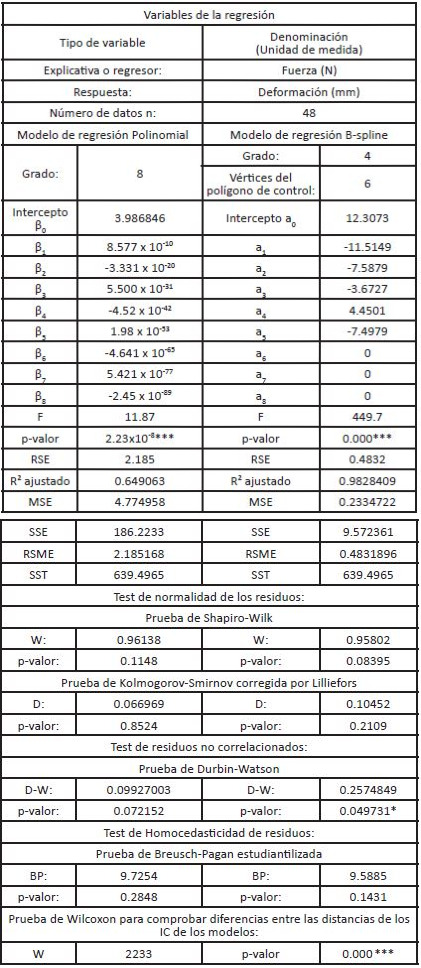
Fuerza vs Deformación
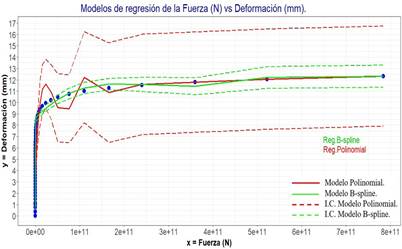
En la Figura 6 se presenta la gráfica de dispersión de puntos de la fuerza versus la deformación se indica, conjuntamente con las curvas de los dos modelos de regresión y las líneas de los intervalos de confianza al 95%:
En la Tabla 6 se presentan los modelos de regresión polinomial y B-spline de la variable fuerza en Newton versus la variable deformación en milímetros:
La distribución de los puntos sigue una curva con forma parecida a una función logarítmica.
Conforme se incrementa la fuerza de impacto del auto sobre la carrocería del autobús también aumenta la deformación de la estructura, aunque el ritmo de crecimiento va disminuyendo a medida que la fuerza se hace más grande.
La curva del modelo polinomial no ofrece un ajuste aceptable, por lo que el modelo es rechazado, también se observa que el intervalo de confianza al 95% es demasiado ancho al mismo tiempo que la curva tiene aristas en forma de dientes de sierra. Por el contrario, la curva del modelo de regresión B-spline brinda un ajuste aceptable a pesar de que existen algunos puntos que quedan fuera de intervalo de confianza.
El modelo de regresión B-spline tiene una menor longitud del intervalo de confianza, lo que significa que tiene una mejor capacidad de minimizar los residuos. Por consiguiente, la relación de la variable explicativa fuerza de impacto y la variable respuesta deformación de la estructura tubular de acero de la carrocería del autobús, se expresa mejor a través de la regresión no paramétrica B-spline de grado 4.
DISCUSIÓN
Los resultados obtenidos se muestran en la Tabla 7. Se establecieron cuatro modelos de regresión simples polinomiales e igual número de modelos de regresión B-splines para el problema de la simulación de impacto de un vehículo en la parte posterior de la carrocería de un autobús.
En cuanto a la bondad de ajuste, el coeficiente de determinación R2 ajustado en todos los casos analizados presentó un valor cercano a 1 y el test F de bondad de ajuste de la tabla ANOVA arrojó que los modelos son idóneos sin mayor complicación.
Tabla 7 Resumen general para comparación de los dos modelos de regresión
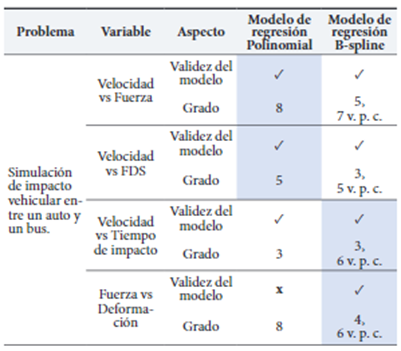
Modelo válido. x Modelo no válido. v. p. c. vértices del polígono de control
Sombreado en color azul el modelo más apropiado en cada caso
ramétricos polinomiales se ajustan bien cuando las curvas tienen forma parabólica o siguen un patrón sin cambios abruptos de curvatura. Mientras que los modelos de regresión no paramétricos B-spline brindan un mejor ajuste cuando las curvas tienen forma de campana con cambios de curvatura más abruptos. Ateniendo al principio de simplicidad de los modelos y que éstos no afecten el suavizamiento del modelo, se consideraron modelos polinomiales de hasta grado 8 y B-splines de hasta grado 5 con 7 vértices de control.
En la práctica no se suelen establecer modelos de regresión con polinomios de grado elevado, debido a la complejidad para la obtención de los valores de la variable respuesta a partir de los valores de la variable regresora.
Una desventaja de obtener modelos complejos es que no resulta factible determinar una relación de crecimiento directa o inversamente proporcional entre las variables.
Por este motivo los modelos de regresión estudiados pueden resultar útiles para la predicción de los valores de las variables respuesta, pero no para resolver problemas de clasificación que son de interés en el ámbito de aprendizaje automático, que suelen establecerse con regresiones lineales 24.
La regresión polinomial tiene una estructura más sencilla, dado que consiste en una expresión algebraica con la variable elevada a distintos exponentes en forma progresiva, ajustada con el uso de coeficientes 25.
De su parte la regresión B-spline está estructurada por una base formada por curvas splines que también tienen polinomios y en los que es necesario establecer un determinado número de vértices del polígono de control 26.
Sedebe destacar la utilidad prácticade la aplicación de los modelos de regresión en la simulación de impacto como parte del diseño de la estructura de la carrocería de autobuses, se detectó que la fuerza del impacto crece ostensiblemente a medida que se va incrementando la velocidad del vehículo que está en movimiento, el FDS de diseño también aumenta con la velocidad al igual que el tiempo de impacto, pero de forma más lenta.
El FDS cuanto mayor es, implica que se necesitará sobredimensionar el diseño, lo que implica utilizar un espesor mayor para el diseño de la estructura del autobús 4. En cuanto a la relación de la fuerza de impacto con la deformación de la estructura del autobús se observó que a partir de la magnitud de fuerza de 1011 N la deformación tendió a ser constante.
En cuanto a investigaciones similares desarrolladas acerca de la relación entre las magnitudes velocidad y tiempo de impacto en las colisiones vehiculares, se puede destacar la llevada a cabo por parte de Mastandrea y Vangi. Los investigadores hallaron una relación directamente proporcional entre la velocidad y el tiempo de duración del impacto en un vehículo golpeado por otro, aunque los rangos de velocidades fueron menores a los del presente estudio, sin embargo, la curva muestra una tendencia creciente similar a la de la Figura 5, lo que corrobora la relación existente entre ambas magnitudes 27.
CONCLUSIONES
Los modelos estadísticos de regresión paramétrica polinomial y no paramétrica B-splines tienen sus propias particularidades. En el primer caso, demanda el cumplimiento de supuestos para los residuos: distribución normal, no autocorrelación y homocedasticidad.
La estructura de un modelo de regresión polinomial consiste en una expresión algebraica con la variable elevada a exponentes consecutivos de entre los cuales el mayor determina el grado del polinomio y para el ajuste se emplean diferentes coeficientes para cada término.
La regresión B-spline está estructurada por una base formada por curvas splines y en los que es necesario establecer un determinado número de vértices del polígono de control.
En el fenómeno simulado se estableció como variable regresora a la velocidad del auto pequeño en el momento de la colisión, cuyos valores oscilaron entre 45 y 95 km/h.
Según la distribución de los puntos de la velocidad versus la fuerza, son directamente proporcionales, la elevación de la velocidad provocó que la fuerza tienda a incrementarse ostensiblemente, con un rango de valores fluctuantes entre 11935 y 2.47 x 10¹² N.
La distribución de los puntos de la velocidad versus el FDS y de la velocidad vs el tiempo de impacto también expresaron relaciones directamente proporcionales, siendo que los rangos de datos fluctuaron entre 1 y 33.66 para el FDS, y entre 0 y 0.67 segundos para el tiempo.
La distribución de puntos de la fuerza de impacto versus la deformación en la estructura es directamente proporcional, aunque la deformación tendió a presentar incrementos menores conforme se eleva la fuerza de impacto. El rango de datos de deformación osciló entre 0 y 13.11 mm.
La relación de la velocidad y la fuerza se explica de manera óptima mediante un modelo de regresión polinomial de grado 8. La relación de la velocidad y el FDS mediante un modelo de regresión polinomial de grado 5. La relación de la velocidad y el tiempo de impacto se explica con un modelo de regresión polinomial cúbico. La fuerza y deformación se relacionan con un modelo de regresión B-spline de grado 4, con 6 vértices del polígono de control.
Los modelos de regresión paramétricos polinomiales se ajustan bien cuando las curvas tienen forma parabólica o siguen un patrón sin cambios abruptos de curvatura, adaptándose mejor a las relaciones de la simulación de impacto vehicular. Por su parte, los modelos de regresión no paramétricos B-splines brindan un mejor ajuste cuando las curvas tienen forma de campana con cambios de curvatura más abruptos.
En el diseño de las carrocerías de autobuses se recomienda hacer ensayos experimentales en diferentes escenarios, tanto para los vehículos que como para varios materiales constructivos. Adicionalmente se sugiere desarrollar investigaciones destinadas a comparar los dos modelos aquí estudiados, pero destinados a otras aplicaciones, para corroborar los resultados obtenidos en este trabajo.