Forma sugerida de citar:
García-Lázaro, D. y Martín-Nieto, R. (2023). Competencia matemática y digital del futuro docente mediante el uso de GeoGebra. Alteridad, 18(1), 85-98. https://doi.org/10.17163/alt.v18n1.2023.07
1. Introducción
La adquisición de una competencia matemática básica es una de las metas a alcanzar en los Objetivos de Desarrollo Sostenible de 2030 previstos por la ONU. En concreto, el ODS número cuatro (ODS4) recoge la necesidad de lograr una educación universal y de calidad. Por tanto, para conseguir este objetivo es importante analizar la relación existente entre los resultados obtenidos en las aulas y la formación académica recibida por el profesorado y el futuro docente en formación.
Para ello, el Informe PISA (Programme for International Student Assessment) facilita información educativa sobre los niveles de conocimiento y competencias adquiridos por el alumnado a nivel internacional, lo que posibilita vislumbrar las áreas de conocimiento que mejoran en un territorio y las que aún son mejorables (OCDE, 2019). Los resultados obtenidos por España en el área de matemáticas en los últimos años se sitúan por debajo de la media de la OCDE, así como de los países vecinos.
Además, el National Council of Teacher of Mathematics (NCTM, 2020) recoge los estándares para la preparación de profesores de matemáticas tanto para educación infantil (De Castro Hernández, 2020) como para primaria en general. En concreto, para geometría, se pretende que se apliquen las transformaciones y se utilice la simetría para analizar situaciones matemáticas (NCTM, 2020).
La ley educativa que regula los conocimientos básicos de la primaria en España (BOE, 2020) recoge la necesidad de que el alumnado adquiera una destreza matemática suficiente como para que pueda desenvolverse en su vida diaria y formativa. Esta destreza supone la resolución de problemas matemáticos (que como actividad compleja e integral requiere una formación específica unida a conocimientos cognitivos y metacognitivos) para alcanzar los elementos constitutivos de la competencia (Pistón-Rodríguez y Parejo-Jiménez, 2019) y que deberían ser adquiridos en las primeras etapas formativas.
Las matemáticas se consideran la base de procesos complejos del conocimiento y que requieren de otras habilidades como pensamiento analítico, reflexivo y crítico, es decir, capacidad para el razonamiento, la formulación o resolución de problemas (Fernández Bravo, 2006). De ahí la importancia de que todas las personas puedan adquirir durante su formación las competencias matemáticas básicas y que puedan consolidar contenidos matemáticos más complejos. La labor del docente es muy relevante en esta tarea, ya que requiere de habilidades didácticas y metodológicas para poder resolver posibles dificultades y facilitar el aprendizaje (Saucedo et al., 2014). De igual manera, el docente, deberá “desarrollar su capacidad argumentativa, el uso del léxico matemático apropiado, y el adecuado uso de diferentes representaciones de un objeto matemático acompañado de material manipulativo o recursos tecnológicos, según sea el caso” (Vargas-Díaz y Apablaza, 2019, p. 87).
Según Rivero (2012), enseñar matemáticas supone ser consciente también de algunas dificultades, como podrían ser: la abstracción en la impartición de la materia, el uso de repetición memorística, mecanizada o la metodología poco adecuada que no facilita la comprensión de los conceptos matemáticos; todo esto unido a cómo los estudiantes sienten las matemáticas, que suele mostrarse como odio, rechazo o ansiedad hacia ellas (Novelo Sánchez et al., 2015).
Una vez que los futuros docentes adquieren los conocimientos y la competencia matemática básica, se hace necesario contar también con la competencia comunicativa y didáctica suficiente, que facilite una transmisión eficaz de la materia. Se trata de “un proceso que otorga mayor connotación y sentido al proceso formativo” (Jerez Berrio, 2020, p. 13) y que requiere, además de una comunicación interpersonal eficaz y una destreza en el uso de la tecnología con fines didácticos en el aula.
Así, los futuros maestros tienen el reto de, además de dominar el área matemática, contar con destrezas en la competencia digital y comunicativa (Gràcia et al., 2017; 2020) para realizar de manera eficaz la transmisión del conocimiento. Estas competencias, como concluyen Colás-Bravo et al. (2019, p. 30), “trasciende más allá de la formación individual del profesorado en materia TIC, siendo necesario el desarrollo de prácticas docentes generadoras de esta en el alumnado”.
Una de las estrategias que surgen para mejorar esas competencias, es integrar las tecnologías como herramienta para el acercamiento al contenido matemático y alcanzar un mayor atractivo hacia la materia. Para autores como Cotic (2014), su integración en el aula depende del interés del docente y de su capacidad para estimular el trabajo colaborativo del alumnado y el longlife learning o aprendizaje continuo. Pero no solo eso, sino también su habilidad para el manejo y gestión de las propias tecnologías que pasan por su competencia digital (Ortega-Sánchez et al., 2020).
Es evidente que las herramientas digitales juegan un papel importante en el proceso de enseñanza y aprendizaje de las matemáticas en todos los niveles educativos, por ello, el uso didáctico de la tecnología, obliga a tener que adaptar los recursos tradicionales a los digitales. Como afirma Gómez-Gómez (2021), el problema o la dificultad de estos es su adaptación con fines pedagógicos.
Por ello, algunos modelos metodológicos, como Technological Pedagogical Content Knowledge (TPACK), señalan que, para obtener resultados óptimos al integrar la tecnología en el proceso formativo, debe hacerse teniendo en cuenta tres aspectos fundamentales: el dominio de la materia, la aplicación de la tecnología a ella y el componente pedagógico de la misma. Es lo que el TPACK clasifica en tres bloques: el Conocimiento Tecnológico, el Conocimiento del Contenido y el Conocimiento Pedagógico (Schmidt et al., 2009).
Otros modelos como NETS-T Standards, de la ISTE International Society for Technology in Education, analizan perfiles tecnológicos para la preparación de los y las docentes y su vinculación con la competencia mediática (Fuller, 2020). En el contexto de la competencia digital, uno de los modelos más conocidos es el European framework for the digital competence of educators: DigCompEdu (Redecker, 2017), en España, el Marco Común de Competencia Digital Docente (INTEF, 2017)
El informe TEDS-M (Teacher Education Study in Mathematics) de la IEA (Instituto Nacional de Evaluación Educativa) de 2012, señala que la formación del profesorado en Educación Matemática es una de las variables que interfieren en las diferencias internacionales existentes entre los resultados académicos de los niños y niñas de Educación Primaria y Secundaria. La prueba distingue entre el Conocimiento del Contenido de las Matemáticas (MCK) y el Conocimiento del Contenido Pedagógico de las Matemáticas (MPCK) que representaran toda la gama de dificultad.
En concreto en el Informe TEDS-M (2012), se muestra cómo los futuros maestros reconocen tener menos formación en el ámbito de la geometría que el resto del alumnado de otros países, aunque se encuentran prácticamente al mismo nivel en los otros bloques.
Por tanto, teniendo en cuenta los principios del modelo metodológico TPACK y los resultados del Informe TEDS-M (2012), en concreto el módulo de Geometría, se analizan seis ítems de 24 que corresponden al contenido matemático y 2 de 10 al Contenido Pedagógico, para el diseño de esta investigación.
En los últimos años, la educación en las primeras etapas ha sido testigo de los cambios que la tecnología ha provocado en la manera en que el alumnado se acerca al conocimiento y al ocio, y de cómo se abre un amplio abanico de posibilidades para su uso didáctico en las aulas. Referirse a la competencia digital, supone ir más allá del conocimiento instrumental del mero uso de los equipos (Eshet-Alkalai, 2012), para entenderla como “combinación de un conjunto de habilidades técnico-procesales, cognitivas y socioemocionales, necesarias para vivir, aprender y trabajar en una sociedad digital” (Fraser et al., 2013). Con este paradigma, de esta competencia digital se deriva el desarrollo del pensamiento crítico, así como otras habilidades creativas e intelectuales. Por tanto, la utilización básica de la tecnología, de la que generalmente parten el futuro profesorado y su alumnado, es solo la base previa para alcanzar la plena competencia digital (European Commission, 2011). Ya en 2012, Ferrari recoge la definición del Institute for Prospective Technological Studies (IPTS) para la Comisión Europea que determina la competencia digital como:
Conjunto de conocimientos, habilidades, actitudes, estrategias y valores que se requieren cuando se utilizan las TIC y los medios digitales para realizar tareas, resolver problemas, comunicarse, gestionar información, colaborar, crear y compartir contenidos, y construir conocimiento de manera eficaz, eficiente, apropiada, crítica, creativa, autónoma, flexible, ética y reflexiva para el trabajo, el ocio, la participación, el aprendizaje, la socialización, el consumo y el empoderamiento.
Así, hay trabajos (por ejemplo, Esteve Mon, 2015) que entienden la competencia digital como la acumulación de conocimientos diversos: comunicativo, tecnológico, audiovisual o mediático.
De esta manera, en función del punto de partida de cada estudiante, habrá quienes tengan “habilidades y destrezas dentro de los circuitos de producción y transferencia de los nuevos conocimientos (digitales)” y otros que no, lo que puede producir una brecha digital (Didriksson, 2007, p. 58) si no se alcanzan destrezas, según la UNESCO, en cuatro niveles: a) acceso; b) uso; c) apropiación y d) producción.
Existe consenso en creer que la tecnología facilita a los equipos docentes incluir recursos diversos que permitan alcanzar la búsqueda de formación de calidad, lo que es esencial en la enseñanza y el aprendizaje de las matemáticas (Hohenwarter et al., 2009). Además, a través de ella el alumnado puede adquirir muy diversas habilidades matemáticas con entornos multimedia, aprovechando sus destrezas digitales. Como recuerdan Rubio et al. (2016, p. 91), “las ventajas de integrar las tecnologías digitales —por ejemplo, software de geometría dinámica, CAS, hoja de cálculo, entre otros— en la Educación Matemática” han sido ampliamente reseñadas en la literatura especializada (Artigue, 2009; Hoyles, 2010) y facilitan la apertura hacia procesos de interacción pedagógica, de colaboración y de compartir conocimientos (Barahona et al., 2015).
Los recursos tecnológicos pueden facilitar, activar y desarrollar los procesos de adquisición de estas competencias y pueden ser desarrolladas eficazmente con la aplicación de softwares matemáticos como GeoGebra, como han determinado investigaciones anteriores (Aldazábal Melgar et al., 2021; Septian et al., 2020; Suryani y Rofiki, 2020; Freyre y Mántica, 2017).
La aplicación, creada por Markus Hohenwarter, ofrece la posibilidad de aprender geometría dinámica (Geo) y álgebra (Gebra), así como muchos otros contenidos matemáticos en los currículos de primaria, secundaria o bachillerato (De Albornoz Torres, 2010) en un entorno de software conectado, compacto y fácil de usar (Diković, 2009). Se trata de un recurso sencillo pero potente.
Entre las características de GeoGebra están, el diseño, a través de software libre que facilita su desarrollo continuo; la sencillez de uso; la posibilidad de utilizarlo en diferentes plataformas y múltiples idiomas, así como el aprendizaje por descubrimiento experimental y guiado (Diković, 2009). Además de contar con una interfaz sencilla y una gran variedad de herramientas geométricas y algebraicas para realizar numerosas construcciones; se pueden “realizar conjeturas, generalizaciones e incluso intuir qué formas se pueden obtener en ciertas condiciones” (Bolaños y Ruiz, 2018, p. 156). Por su parte, Barahona et al. (2015) destacan que GeoGebra facilita procesos de abstracción para mostrar relaciones entre un modelo geométrico y otro algebraico de una situación de la vida real. Posee una hoja de cálculo y sus numerosas vistas permiten alternar el uso de la aritmética, representaciones algebraicas, cálculo simbólico y cálculo estadístico y probabilístico (Del Pino Ruiz, 2013), lo que facilita resolver un problema, no solo de manera matemática, sino también de manera visual (Aktümen y Kabaca, 2012). Además, GeoGebra favorece el trabajo colaborativo y constructivista con interacción entre distintos grupos de trabajo y el interaprendizaje (Prodromou, 2014).
A la hora de evaluar la competencia matemática del futuro docente para el caso español se pueden considerar las siete capacidades específicas que establece el Informe PISA (OCDE, 2019): comunicación, matematización, representación, razonamiento y argumentación, diseño de estrategias para resolver problemas, utilización de operaciones y lenguaje simbólico, formal y técnico, y utilización de herramientas matemáticas; así como los estándares de aprendizaje de NCTM. Esta concreción facilita la evaluación y medida de adquisición del grado de competencia matemática que determina el currículo en cada etapa educativa.
Entre los conocimientos y habilidades que se circunscriben de manera destacada a la competencia matemática, tal y como se ha recogido anteriormente, están las que giran en torno a la geometría y el álgebra y que recoge también el ODS4.
Por tanto, el objetivo de esta investigación es trabajar desde el punto de vista competencial los logros de aprendizaje para la geometría que establece NCTM combinando la competencia didáctica, digital y matemática (Modelo TPACK) con la aplicación del Software GeoGebra Classic en la formación universitaria que recibe el futuro profesorado, así como conocer la percepción que tienen por la inclusión de estas iniciativas en el aula.
2. Metodología y diseño de la investigación
La investigación que se presenta surge de la necesidad de incorporar a la didáctica tradicional de las matemáticas, una herramienta digital que permita al alumnado universitario en formación, conocer cómo se resuelven problemas matemáticos aplicando el Software informático GeoGebra Classic. Se busca no solo la resolución de ejercicios limitándose a la obtención del resultado final óptimo (conocimiento matemático adquirido), sino que el empleo de esta herramienta digital (competencia digital) suponga parte del proceso de formación complementario a la mera utilización de lápiz y papel, y que simulen su aplicación en un aula real (competencia didáctica), en definitiva, se pretende cumplir con los pilares que establece el Modelo Metodológico TPACK.
Para ello, se ha llevado a cabo una prueba piloto en la asignatura Matemáticas y su Didáctica III, perteneciente al tercer curso del Plan de Formación de los Grados en Educación Primaria de la Universidad Rey Juan Carlos durante el curso 2021-2022, a través de la utilización de una metodología mixta con diseño preexperimental en la que participa una muestra de 68 matriculados.
El curso se caracteriza por el inicio de las clases en formato híbrido debido a la Covid-19, en el que, por turnos, se compagina la asistencia presencial y telemática a las clases.
2.1 Objetivos
El objetivo general es conectar la tecnología, las matemáticas y la didáctica con el propósito de incorporarlas en la formación del profesorado utilizando la herramienta de GeoGebra Classic.
Los objetivos específicos son:
OE1 (Conocimiento de Contenido): trabajar la geometría como contenido de aprendizaje para el futuro maestro.
OE2 (Conocimiento Tecnológico): trabajar la geometría con herramientas digitales para la incorporación de la competencia digital a la matemática y viceversa.
OE3 (Conocimiento Pedagógico): trabajar los contenidos relacionados con la geometría de educación primaria con el programa GeoGebra Classic.
2.2 Muestra
Esta investigación se lleva a cabo durante el primer semestre del curso 2021-2022 con alumnado perteneciente al Grado de Educación Primaria (85,29 % de la muestra) y al Doble Grado en Educación Infantil y Primaria (14,70 % de la muestra), ambas titulaciones de carácter presencial y con una población de 68 matriculados, de los que el 58,82 % son hombres y 29,41 % son mujeres. El muestreo realizado es de tipo no probabilístico, por conveniencia y además pertenecen a un grupo único, por lo que representa al cien por cien de la población objeto de estudio.
2.3 Fases de la investigación
En la primera clase se hizo un braimstorming utilizando la herramienta Wooclap, en la que se preguntaba al alumnado sobre cuál era su percepción de las matemáticas en general y de la geometría en particular. La mayoría del alumnado participante en la modalidad en la modalidad remota, a través de la plataforma Teams, así como los que estaban presencialmente en el aula, coincidían en que les resultaban difíciles y aburridas. Además, se les preguntó qué les parecería el hecho de “enseñar matemáticas” como futuros docentes, y la mayoría reconocían que les ponía nerviosos y que no se sentían preparados. Tras este primer análisis, se les preguntó sobre el conocimiento de programas informáticos para el tratamiento y didáctica de la geometría, y aunque muchos desconocían su existencia con fines didácticos, sí que conocían la aplicación de GeoGebra en la resolución de problemas, además algunos señalaban que lo habían trabajado en cursos anteriores.
Tras la primera toma de contacto con la participación en Wooclap, se propuso al alumnado realizar un taller virtual con el uso de GeoGebra Classic para trabajar los contenidos matemáticos que se recogen en este módulo. Para ello, debían formar grupos de trabajo, con roles asignados propios del trabajo cooperativo (Johnson y Johnson, 1999).
Para llevar a cabo el taller, se les plantea realizar el análisis de los contenidos de dos documentos, por un lado, la guía docente de la asignatura, y por otro, el análisis del Decreto 89/2014 por el que se regulan los contenidos matemáticos para el Ciclo de Educación Primaria para la Comunidad de Madrid, España. El objetivo es conocer cuáles son los estándares de aprendizaje que se les exige a ellos en la materia y qué correspondencia existe entre estos y los contenidos curriculares regulados en los centros educativos donde se incorporarán como docentes cuando egresen.
En la segunda fase, se les pide trabajar de manera didáctica las transformaciones, en concreto los movimientos rígidos y la homotecia. Para ello, desarrollaron materiales didácticos apoyándose en materiales manipulativos adaptados como si fueran a aplicarlos en el aula real.
Una vez completada esta actividad, se les propuso que resolvieran una serie de ejercicios sobre la misma temática utilizando herramientas como el compás y la regla, dinámica que en un principio debían desarrollar a nivel individual.
Por último, se les pidió que estos mismos ejercicios, los resolvieran aplicando el programa GeoGebra Classic.
2.4 Aplicación de GeoGebra Classic en el aprendizaje de las transformaciones geométricas
A continuación, se realiza un análisis de caso para entender mejor la dinámica de la aplicación de GeoGebra Classic en el taller virtual diseñado para ello.
En el primer ejercicio que se les plantea, el alumno/a tiene que realizar un giro en sentido antihorario del siguiente sector circular, tomando como centro de giro el punto D y ángulo de giro el ángulo α.
Las valoraciones a las que se acoge la resolución recogida en la rúbrica proporcionada por el docente son:
No aporta el ejercicio solicitado.
Aporta el ejercicio, pero no realiza el movimiento requerido.
Aporta el ejercicio y realiza el movimiento requerido, pero le falta tener en cuenta el sentido, o el centro o el ángulo solicitado.
Aporta el ejercicio y realiza bien el movimiento requerido teniendo en cuenta el sentido, el centro y el ángulo solicitado.
La figura 2 muestra una de las producciones correctamente resuelta.
Los criterios de valoración entres pares se han realizado con base en una rúbrica que proporciona el profesorado y un apartado de retroalimentación libre. Las valoraciones coincidentes otorgadas por dos compañeros con base en la rúbrica, y supervisadas por el profesorado, determina la correcta realización del ejercicio.
Por otro lado, a continuación, se muestran dos soluciones sobre otro de los enunciados planteados, una solución correcta y una solución parcialmente correcta. En este caso, se le pide al alumnado que realice una simetría con base en el eje proporcionado. La figura 3 muestra una de las producciones que se considera no del todo correcta recibiendo la valoración de otro compañero/a entre las opciones disponible como “el alumno aporta el ejercicio, pero no realiza el movimiento requerido”.
Sin embargo, en la figura 4, recibe la evaluación positiva aportando correctamente el ejercicio y realizando el movimiento requerido.
En definitiva, la participación en los talleres con la entrega y valoración por pares permitió al alumnado participante conocer la forma de desarrollar los mismos ejercicios por otros compañeros, así como la posibilidad de autoevaluarse e identificar si lo que habían hecho era correcto o no.
2.5 Instrumentos de recogida de información
Para conocer la percepción que tuvo esta iniciativa entre el futuro profesorado y ver qué asociación establecían con la implementación de las actividades propuestas en un aula real, se diseñó un cuestionario ad hoc utilizando la herramienta Forms del Paquete Office 365, como principal instrumento de recogida de información. El cuestionario consta de ocho ítems formados por preguntas dicotómicas y de escala Likert con valores entre 1 y 5, siendo el 1 el peor valor y 5 el máximo valor, con alguna pregunta abierta. El tiempo medio de respuesta es inferior a cuatro minutos. Las preguntas se orientan a la valoración de la experiencia con la participación a través de los talleres, la utilización de GeoGebra Classic y el conocimiento del temario. Asimismo, se les pregunta sobre la percepción que tienen en cuanto a la formación en didáctica de las matemáticas, así como su formación en contenidos matemáticos en los niveles anteriores a cursar el Grado en Educación.
La participación voluntaria en el cuestionario es del 40 % (28 estudiantes), participación menor de la esperada pero que permite realizar un análisis de la situación que facilite la adopción de estrategias didácticas y pedagógicas adecuadas para alcanzar los objetivos docentes con éxito (Hernández Ávila y Carpio Escobar, 2019). Por otro lado, se analizó la participación en los talleres y las puntuaciones obtenidas en estos, así como la repercusión de esta en la calificación final de la asignatura.
3. Resultados
El análisis cuantitativo de las respuestas proporcionadas en el cuestionario se lleva a cabo mediante el paquete estadístico Microsoft Excel, realizando un análisis descriptivo de los resultados. El análisis cualitativo se realiza teniendo en cuenta las aportaciones y opiniones de los participantes tanto de las respuestas obtenidas con Wooclap como de las preguntas abiertas del cuestionario, completando así las informaciones obtenidas en el análisis cuantitativo.
Así, se presenta una clasificación por bloques de la información más relevante:
Formación previa: se les preguntó por la rama de conocimiento previa al acceso a la universidad, y más de la mitad de la clase se identificó con “letras” en el 54 % de los casos mientras que apenas el 48 % se identificaba con “ciencias”.
Contenido: en cuanto a la dificultad del contenido relacionado con la geometría, se les pidió que valoraran mediante una pregunta dicotómica, si este era difícil o fácil o les resultaba incomprensible. La moda indica que perciben los contenidos matemáticos vistos hasta el momento como difíciles o muy difíciles. Bien es cierto que en esta pregunta se les pedía, además, si creían que tenían que estudiar más, siendo que el 74,2 % de los encuestados otorgan una valoración media de 4 puntos sobre 5 a la afirmación sobre que tienen que estudiar más, al menos en el momento en el que contestaron la encuesta, y un 29 % afirmaba no entender nada.
Percepción de la formación: más de la mitad de los informantes creen que el plan de formación de su Grado necesita más horas de dedicación a la didáctica de las matemáticas
Valoración del taller: la valoración del taller es positiva en líneas generales. Para conocer la opinión de estos, se dejó esta pregunta abierta para recoger las opiniones de esta. Algunos de los comentarios a destacar son: “GeoGebra me ha ayudado a visualizar lo que de forma abstracta no lograba ver por mí misma” “el hecho de hacer ejercicios en GeoGebra me parece un buen recurso”. Sin embargo, uno de los aspectos negativos a destacar es que los ha llevado mucho tiempo la realización de ejercicios con la aplicación.
Además, para conocer la participación en el taller, se configuraron dos actividades en el aula virtual, por un lado, la entrega de la tarea programada en la que cada coordinador del grupo debía entregar las actividades diseñadas con material manipulativo en tiempo y formato establecido. En este caso, la participación fue del 100 % de los matriculados, dato relevante puesto que la participación era una decisión voluntaria. Por otro, se configuró un taller virtual para la entrega a nivel individual de la solución de ejercicios propuestos. En este caso, se dividió en dos sesiones, por un lado la entrega y por otro la evaluación del trabajo de otro/a compañero/a para fomentar la evaluación entre iguales. En la primera fase participaron el 89,65 % de los matriculados, sin embargo, en la evaluación del trabajo de un/a compañero/a participó el 83,82 %, este dato debe tener en cuenta que los alumnos/as que no entregan su trabajo no pueden evaluarlo.
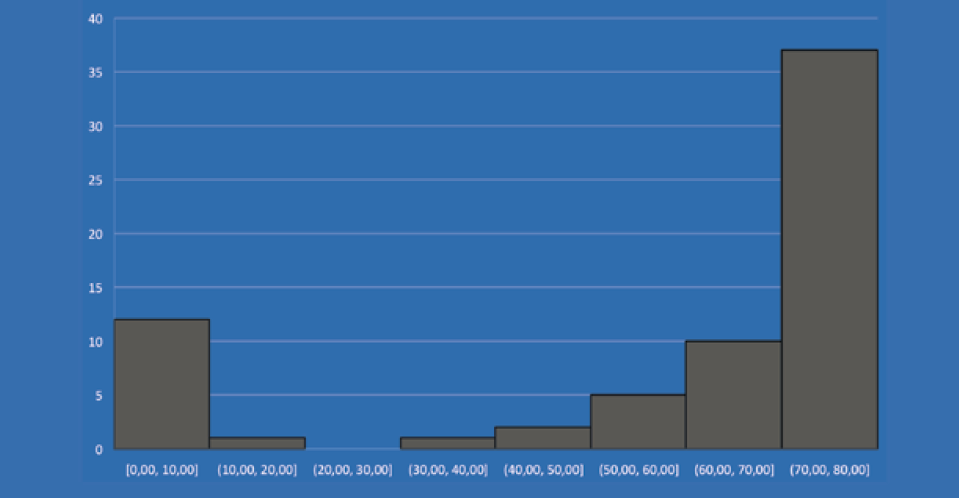
La puntuación media general sobre la participación del taller es satisfactoria ya que oscila entre los 70 y los 80 puntos. En concreto, si se analiza el resultado medio del primer ejercicio planteado a modo de ejemplo, se obtiene una puntuación de 78 puntos sobre 80. En general, como se puede observar en la figura 5, la mayoría del alumnado obtuvo esta calificación porque resolvieron correctamente el ejercicio planteado aplicando GeoGebra Classic.
4. Discusión y conclusiones
Los resultados presentados indican que la aplicación de la tecnología permite alcanzar resultados óptimos si se combina con el conocimiento y la didáctica en el proceso de enseñanza y aprendizaje de la materia. La inclusión de GeoGebra Classic en el proceso formativo del futuro profesorado y la introducción en el aprendizaje de conceptos matemáticos han tenido buena aceptación entre el alumnado, mientras que, como afirma Gómez-Gómez (2021), la aplicación de distintos recursos tecnológicos con fines pedagógicos permite alcanzar mejores resultados. En la misma línea, estudios como el de Rubio et al. (2016), señalan que las TIC mejoran la competencia tecnológica, entre otras cosas, porque se desarrolla el pensamiento abstracto. Durante el proceso se ha determinado que al igual que ocurría en las investigaciones anteriores como la de Ruiz López (2012), la competencia didáctica mediante el uso del GeoGebra Classic puede estar condicionada por la competencia digital previa que tenga el alumnado, por lo que es necesario implementar actividades en el aula que faciliten alcanzar la competencia durante los procesos de formación de los futuros docentes, para que estén más en consonancia con la situación actual de la educación en España.
El alumnado puede adquirir la competencia matemática según el modelo TPACK, y como se afirma en el estudio de Mishra y Koehler (2008), si se combina la dimensión tecnológica y las destrezas del alumnado con los conocimientos matemáticos adquiridos y su aplicación en el aula. Por otro lado, otras investigaciones, como la de Pistón-Rodríguez y Parejo-Jiménez (2019), destacan que la competencia matemática se adquiere en las primeras etapas formativas; sin embargo, la evidencia empírica de este trabajo muestra que la aplicación de GeoGebra Classic permite al alumnado reconocer el componente abstracto de las matemáticas, tal y como asegura la mayoría de los encuestados participantes; lo que se relaciona, a su vez, con las investigaciones realizadas por Fernández-Bravo (2006) en las que concluye que se pueden adquirir competencias matemáticas básicas en cualquier etapa formativa, o con el análisis sistemático realizado por Yohannes y Chen (2021) de las investigaciones que resaltan la importancia de la integración de Geogebra para la educación matemática.
Desde el punto de vista de la competencia matemática adquirida, los resultados demuestran una mejora en las calificaciones de aquellos estudiantes que participaron individualmente en los talleres con GeoGebra Classic. Es especialmente destacable la ruptura de la diferencia de conocimientos previos que algunos estudiantes presentaban en la asimilación y aplicación de los conceptos matemáticos y que estaba condicionada por su rama de conocimiento previa identificada con el campo de las humanidades y no de las ciencias. Además, esto les ha servido para demandar más formación en este sentido. Por tanto, se eliminan algunas barreras de rechazo ante las matemáticas en general y a la geometría en particular como también concluyen Novelo Sánchez et al. (2015).
Por otro lado, es de especial interés la competencia didáctica y mediática del docente para facilitar el acceso del estudiantado a los conocimientos, así como favorecer el acceso a recursos digitales que faciliten el acercamiento a los conocimientos matemáticos básicos mientras desarrollan la competencia. Se destaca la necesidad de dotar de competencias digitales docentes al futuro profesorado a través de la adecuada inclusión de las TIC, y donde el modelo TPACK se muestra como un modelo de enseñanza eficaz.
En definitiva, la aplicación de GeoGebra Classic facilita y mejora la adquisición de competencia matemática y digital y reduce determinadas carencias o dificultades que surgen en el aprendizaje. La principal aportación de la aplicación de la metodología mixta preexperimental, diseñada para la presente investigación con el uso de talleres y la aplicación de GeoGebra Classic, es que existe replicabilidad en el procedimiento y permite desarrollar estrategias que combinen a la vez, las tres competencias previstas en el modelo TPACK.
Sin duda, un buen punto de partida para completar esta investigación sería realizar un estudio comparativo entre los resultados de promociones futuras con los obtenidos en este trabajo observando las desviaciones existentes con el fin de adoptar estrategias de mejora didáctica para alcanzar una docencia de calidad y cumplir eficazmente con los ODS al comprobar que el uso de GeoGebra mejora la competencia matemática digital del futuro docente.