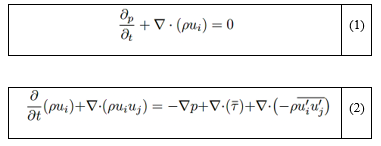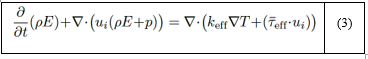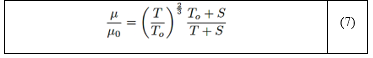Introducción

Las geometrías de las toberas convergente-divergentes utilizadas en el campo aeroespacial influyen significativamente en el desarrollo del campo de flujo. En consecuencia, la geometría de la pared interna de la tobera y la turbulencia del flujo resultante continúan siendo temas recurrentes de interés, particularmente bajo condiciones de flujo viscoso sobreexpandido, adaptado y subexpandido [1]. Desde la aparición de avances tecnológicos en toberas supersónicas, sus geometrías han experimentado una evolución continua para optimizar y regular el tránsito del flujo. Entre las geometrías de toberas más destacadas se encuentran las toberas cónicas, los diseños contorneados o en forma de campana (tanto de longitud completa como acortadas), las toberas tipo tapón o aerospike (de longitud completa y truncadas), las toberas de expansión-deflexión, las toberas planas, entre otras [1-6]. La investigación en esta área se ha extendido al método de las características (MOC) [7, 8], así como al desarrollo de modelos matemáticos aproximados para simular el flujo mediante herramientas de dinámica de fluidos computacional (CFD) [9,10]. Además, los estudios han explorado la solución de modelos matemáticos para flujo isentrópico que involucran ecuaciones analítica que no pueden ser invertidas mediante procedimientos algebraicos [11-14].

Las toberas cónicas supersónicas con un rendimiento óptimo suelen tener un semiangulo divergente α en un rango de 12° a 18°. Cuando α <12°, estas toberas se clasifican como fuera de diseño [1]. El mismo principio se aplica a las toberas planas sin curvatura en la sección divergente.

Bajo condiciones de flujo sobreexpandido, diversos fenómenos de ondas de choque ocurren en la sección divergente de la tobera, incluyendo ondas de choque normales, oblicuas, reflejadas e internas. La Figura 1 ilustra la estructura de ondas de choque en la sección divergente de una tobera supersónica [15], junto con una imagen de una onda de choque capturada mediante la técnica Schlieren, según lo reportado por Hunter [6], [16].

La región central del flujo contiene el frente de choque, flanqueado por ondas oblicuas y reflejadas que interactúan con gradientes de presión y temperatura [6], [17, 18]. En la región de flujo adyacente a las paredes de la tobera, se observan cargas de presión lateral antes y después del choque. La capa límite interactúa con las ondas de choque y, aguas debajo del punto de separación del flujo, se producen contrapresión y recirculación del flujo, acompañadas por la formación de vórtices. Los efectos de la temperatura y la fricción son prominentes en la región de flujo cercana a las paredes, donde se observan fenómenos de separación libre de choque (FSS, por sus siglas en inglés) y separación restringida de choque (RSS) [19-22]. En los bordes de la tobera, como el borde de salida, se generan ondas de expansión de Prandtl-Meyer [17]. El flujo de chorro supersónico descargado a la atmósfera forma una pluma que contiene estructuras de ondas de choque, las cuales están influenciadas por la relación de presión de la tobera (NPR, por sus siglas en inglés) [19].

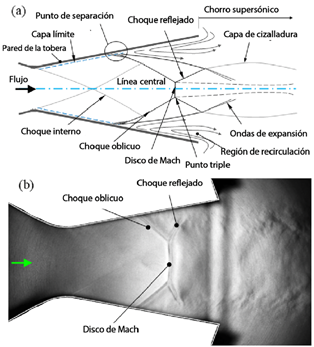
Figura 1 (a) Estructura de ondas de choque para la condición de flujo sobreexpandido [15]. (b) Imagen experimental de la estructura de ondas de choque en una tobera plana, según lo reportado por Hunter [6]. 

Varios estudios significativos han explorado el comportamiento del flujo en toberas fuera de diseño. Hunter [6] hizo pruebas experimentales sobre la separación del flujo en una tobera plana con un ángulo divergente α = 11,01°, revelando que el flujo sobreexpandido estaba dominado por la separación de la capa límite inducida por ondas de choque. De manera similar, Verma y Manisankar [18] investigaron toberas planas con ángulos divergentes α = 5,7°, α = 7,5° y α = 10,7°, identificando asimetría en los frentes de ondas de choque normales, oblicuas y reflejadas, así como una separación no simétrica de la capa límite entre las paredes superior e inferior. Tolentino et al. [23] llevaron a cabo simulaciones computacionales para toberas planas con α = 9°, α = 11,01° y α = 13°, informando que un aumento en el ángulo divergente condujo a un incremento en la velocidad del flujo en la región central a la salida de la tobera. Arora y Vaidyanathan [24] investigaron toberas planas con doble divergencia, encontrando que el ángulo de inflexión influía significativamente en la estructura de las ondas de choque, con una expansión adicional ocurriendo en la segunda divergencia.

Tolentino et al. [25] simularon el campo de flujo en toberas planas con garganta de corte recto para α = 11,01°. Encontraron que, a medida que aumentaba la longitud de la garganta, el tren de ondas de choque evolucionaba dentro de la sección de la garganta, afectando el desarrollo del flujo en la parte divergente.

Mason et al. [26] estudiaron experimentalmente toberas planas con ángulos divergentes α = 1,21°, α = 10,85° y α = 11,24°. Sus resultados mostraron que el contorno convergente y de la garganta afectaba significativamente el comportamiento del flujo. Para α = 1,21°, se observaron fluctuaciones de presión a lo largo de la pared divergente debido a la presencia de un tren de ondas de choque. En contraste, para α = 10,85°, solo se observó un salto de presión en el punto de separación del flujo debido al frente de choque normal.

Tolentino et al. [15] estudiaron toberas cónicas con garganta de corte recto para α = 10°, demostrando que un aumento en la longitud de la garganta provocaba la evolución del tren de ondas de choque y una reducción del empuje en la salida de la tobera. Tolentino y Mírez [27] analizaron, además, los patrones de flujo en toberas cónicas, revelando que una longitud óptima de la garganta previene la formación de un tren de ondas de choque.

Otros estudios experimentales también han investigado el comportamiento del flujo en toberas. Wagner y Schlechtriem [28] examinaron la turbulencia del flujo en toberas planas con curvatura de pared, reportando propagación no simétrica de las ondas de choque. Bourgoing y Reijasse [29] demostraron que la rugosidad de la pared afecta el desarrollo del flujo, lo que da como resultado configuraciones variables de asimetría de las ondas de choque. Faheem et al. [30] realizaron experimentos con toberas que emiten múltiples chorros supersónicos, encontrando que, a medida que aumentaba el número de chorros, la tasa de dispersión disminuía debido a la reducción de la resistencia, con diferencias notables en los núcleos de los chorros supersónicos.

Las simulaciones de dinámica de fluidos computacional (CFD) [9] han demostrado ser efectivas para reproducir la turbulencia del flujo y determinar parámetros termodinámicos en regiones donde la obtención de imágenes experimentales no es factible. Investigaciones recientes se han centrado en modelar la turbulencia para la geometría experimental de tobera plana de Mason et al. [26], con extensiones a geometrías de toberas cónicas.

Este estudio tiene como objetivo analizar el comportamiento de los patrones de flujo en toberas planas y cónicas clasificadas como toberas fuera de diseño. Ambos tipos de tobera comparten dimensiones geométricas idénticas proyectadas en un dominio computacional 2D. La Sección 2 describe la metodología, incluyendo una descripción de la geometría experimental de la tobera utilizada por Mason et al. [26] para registrar lecturas de presión en diferentes relaciones de presión de la tobera (NPR) bajo condiciones de flujo frío. También se detallan los fundamentos matemáticos y los métodos de solución computacional, junto con el análisis de convergencia numérica y la validación del modelo de turbulencia SAS empleado en las simulaciones. La Sección 3 presenta los resultados numéricos, centrados en los campos de flujo del número de Mach y las distribuciones de presión estática. Finalmente, la Sección 4 proporciona las conclusiones del análisis, resumiendo los hallazgos y sus implicaciones para investigaciones futuras.

Materiales y métodos

Experimental Nozzle

La tobera plana experimental (Modelo B1) bajo estudio, como se ilustra en la Figura 2, fue utilizada previamente por Mason et al. [26]. Los experimentos de presión para condiciones de flujo frío se realizaron en el complejo del túnel transónico de 16 pies del NASA Langley Research Center. Estas pruebas experimentales cubrieron un rango de relaciones de presión de la tobera (NPR) de 1,97 a 8,91. La tobera plana [26] fue diseñada para un número de Mach de 2,08, un NPR de 8,81, una relación de área Ae/At = 1, 8, y un semiangulo divergente α = 10,85°, clasificándola como una tobera fuera de diseño, ya que α < 12°. Ae representa el área de salida de la tobera, y At denota el área de la garganta. El ancho de la tobera plana es de 10,157 cm.

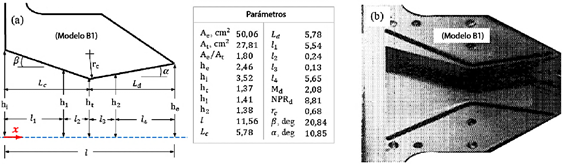
Figura 2 (a) Representación esquemática de la tobera plana, ilustrando los parámetros geométricos (unidades en centímetros). (b) Tobera plana experimental utilizada por Mason et al. [26] para medir la presión del flujo a lo largo de las paredes internas. 

Cabe destacar que las dimensiones geométricas de la tobera plana, cuando se proyectan sobre un plano 2D (Figura 2a), se aplican a la geometría de la tobera cónica. Para la tobera cónica, los radios se definen como hi para la entrada, ht para la garganta y he para la salida, con un semiangulo divergente α = 10,85°. Las condiciones de diseño para la tobera cónica incluyen un número de Mach de 2,713, un NPR de 23,768 y una relación de área Ae/At de 3,224.

Dominio computacional

La proyección espacial de las toberas plana y cónica se consideró en dominios computacionales 2D debido a su simetría. Estos dominios fueron construidos utilizando los datos geométricos reportados por Mason et al. [26], como se muestra en la Figura 2. La Figura 3 ilustra el dominio computacional junto con el dominio mallado para la malla 4, que consta de 30 736 celdas cuadriláteras. La malla 4 representa una malla refinada con una mejor distribución de celdas, previamente evaluada en cuanto a su rendimiento en comparación con otros dominios mallados. Las dimensiones geométricas están parametrizadas, con la línea central alineada a lo largo de la dirección x, y la sección divergente denotada como Ld. La sección convergente de la tobera abarca 0 ≤ x/Ld ≤ 1, la sección divergente abarca 1 ≤ x/Ld ≤ 2, y la sección atmosférica se extiende de 2 ≤ x/Ld ≤ 8. Esta configuración del dominio computacional es adecuada para capturar la turbulencia del flujo y simular la formación de la pluma en el chorro supersónico a medida que se descarga en la atmósfera. Es importante destacar que los dominios computacionales 2D son apropiados para geometrías simétricas, lo que ofrece una reducción significativa en el tiempo computacional iterativo y el uso de recursos en comparación con los dominios computacionales 3D.

Figura 3 (a) Dominio computacional 2D que ilustra las condiciones de contorno aplicadas. (b) Malla estructurada para la Malla 4, compuesta por 30,736 celdas cuadriláteras. 

Las condiciones de contorno aplicadas al dominio computacional 2D para las toberas plana y cónica son las siguientes: En la entrada de la tobera se especifican los datos de presión de estancamiento P_o para ocho casos correspondientes a relaciones de presión de la tobera (NPR) de 1,97, 2,94, 3,92, 4,88, 5,84, 6,81, 7,79y 8,91, donde NPR = Po/P y la presión de la atmósfera local P = 101,3 kPa. La temperatura total T_o se establece en 300 K para los ocho casos. En la salida de la tobera, la presión y temperatura atmosféricas locales se establecen uniformemente en P = 101,3 kPa y T = 300 K para todos los casos. Es importante destacar que los datos de presión y temperatura fueron obtenidos del trabajo de Mason et al. [26].

Las paredes de la tobera se modelan como adiabáticas, lo que significa que no ocurre transferencia de calor a través de ellas. La malla se refina en las regiones adyacentes a las paredes para tener en cuenta la presencia de tensiones cortantes del flujo. En las paredes, la velocidad del flujo es cero debido a la condición de no deslizamiento. A lo largo de la línea central, la velocidad del flujo es cero en la dirección perpendicular para la tobera plana y en la dirección radial para la tobera cónica. Los efectos de la gravedad sobre la turbulencia del flujo se descartan, ya que los dominios computacionales son bidimensionales y representan geometrías simétricas.

El flujo de aire se trata como un gas ideal con las siguientes propiedades termodinámicas: constante de gas R = 287 J/(kg · K), relación de calores específicos k = 1,4, calor específico a presión constante Cp = 1006,43 J/(kg · K) y conductividad térmica kt = 0,042 W/(m · K) [31].

Fundamentos matemáticos

La turbulencia del campo de flujo viscoso en un estado transitorio se simula utilizando el software ANSYSFluent R16.2 [31], que emplea el método de volúmenes finitos (FVM) [9]. Se utilizan las ecuaciones de Navier-Stokes promediadas por Reynolds (RANS), ya que proporcionan un marco eficiente y adecuado para obtener soluciones aproximadas de la turbulencia en flujo compresible. Las ecuaciones gubernamentales para el cálculo del flujo compresible incluyen la conservación de la masa (ecuación (1)), el momento (ecuación (2)) y la energía (ecuación (3)) [9, 10], [31]. Estas ecuaciones, expresadas en forma compacta, son las siguientes:

Donde t es el tiempo, ρ es la densidad, u es la velocidad, p es la presión y τ es el tensor de tensiones. El término −𝜌 𝑢 𝑖 ′ 𝑢 𝑗 ′ representa el estrés de Reynolds, donde se aplican modelos de turbulencia para cerrar la ecuación (2). Además, E denota la energía total, k_eff es la conductividad térmica efectiva, T es la temperatura y 𝜏 𝑒𝑓𝑓 es el tensor efectivo.

El flujo se modela como un gas ideal; por lo tanto, se aplica la ecuación de estado del gas ideal (ecuación (4)). Las ecuaciones para la relación de presiones (ecuación (5)) y la temperatura (ecuación (6)) se expresan como funciones del número de Mach:

Donde R es la constante universal del gas ideal, P_o es la presión de estancamiento, P es la presión estática, T_o es la temperatura de estancamiento, T es la temperatura estática, y k es la relación de calores específicos. El número de Mach, denotado como M, se clasifica de la siguiente manera: flujo subsónico 0,3 ≤ M ≤ 0,8, flujo transónico 0,8 ≤ M ≤ 1,2, flujo supersónico 1,2 ≤ M ≤ 5, flujo hipersónico M > 5, y flujo sónico M = 1. Para flujo incompresible, se considera M < 0,3 [32].

Se empleó el modelo de simulación escalaadaptativa (SAS) [33] para simular la turbulencia del flujo viscoso en un estado transitorio. Además, se aplicó la ley de Sutherland [10], [32] para modelar la viscosidad del flujo como una función de la temperatura. La ley de Sutherland, derivada de una aproximación de la teoría cinética de los gases, tiene en cuenta la idealización de los potenciales de fuerza intermolecular y se expresa como se ve en la ecuación (7):

Donde μ es la viscosidad del flujo, μ_o = 1,716 kg/m· s es la viscosidad de referencia, T_o = 273,11 K es la temperatura de referencia, y S = 110,56 K es la temperatura efectiva. La temperatura efectiva S, también conocida como la constante de Sutherland, se encuentra tabulada para diferentes rangos de temperatura dependiendo del tipo de gas.

Análisis de convergencia numérica

Los dominios computacionales fueron mallados utilizando la plataforma ANSYS-Meshing. Se generaron cuatro mallas de celdas cuadriláteras con densidades variables: malla 1 con 19 249 celdas, malla 2 con 25 658 celdas, malla 3 con 27 311 celdas, y malla 4 con 30 736 celdas. El campo de flujo del número de Mach se simuló utilizando el modelo de turbulencia de simulación escala adaptativa (SAS) [33] para una NPR de 8,91. Entre las cuatro mallas, la 4 exhibió los valores más bajos de Y-plus (y+), particularmente en la distribución de tensiones cortantes evaluada a lo largo de la pared de la tobera plana (Figura 4a). En cuanto a los valores de tensión cortante, las curvas para todas las mallas son generalmente consistentes y se superponen, excepto en la región cercana a la salida de la tobera (Figura 4b).

Para el dominio mallado con la malla 4, el modelo de turbulencia SAS [33] se comparó con los modelos de turbulencia DES SA [34], DES SST k − w [35] y DES k − ε [36], como se ilustra en la Figura 4c. Los resultados indican que el número promedio de Mach en la salida de la tobera es similar para los modelos de turbulencia SAS y DES SA, como se muestra en la Tabla 1. El modelo de turbulencia SAS fue seleccionado para simular el campo de flujo debido a su ligera ventaja en la reducción del tiempo computacional durante los cálculos iterativos. La malla 4 (Figura 3b) presenta una malla estructurada compuesta por celdas cuadriláteras, con regiones refinadas en las zonas de flujo adyacentes a la sección convergente (0 ≤ x/L_d ≤ 1) y la sección divergente (1 ≤ x/L_d ≤ 2), así como a lo largo de las paredes. Además, la malla incluye una estructura de celdas distribuida progresivamente en la sección atmosférica (2 ≤ x/L_d ≤ 8).

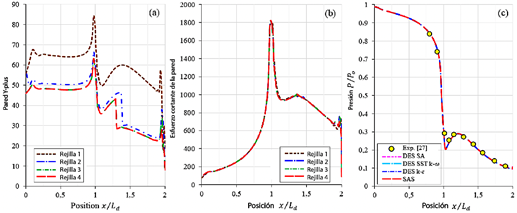
Figura 4 Perfiles de curvas evaluadas a lo largo de la pared de la tobera plana: (a) Y-plus en la pared, (b) Tensión cortante en la pared, y (c) Presión. Posición: sección convergente (0 ≤ x/L_d ≤ 1) y sección divergente (1 ≤ x/L_d ≤ 2). 

Tabla 1 Número promedio de Mach en la salida de la tobera plana para un NPR de 8.91, evaluado utilizando cuatro modelos de turbulencia diferentes 

Resultados y discusión

Esta sección presenta los resultados numéricos para el campo de flujo del número de Mach (Figura 5) y la distribución de presión estática (Figura 6) a lo largo del rango de NPR de 1.91 a 8.91. En las visualizaciones del campo de flujo, las regiones con magnitudes más pequeñas se representan en azul, mientras que las regiones con magnitudes más grandes se representan en rojo. Para la tobera plana, el flujo está sobreexpandido dentro del rango de NPR de 1.91 a 7.79 y se adapta en el NPR 8.91. En contraste, para la tobera cónica, el flujo permanece sobreexpandido a lo largo de todo el rango de NPR de 1.91 a 8.91.

Para la tobera plana, el campo de flujo del número de Mach (Figura 5a) y el campo de presión estática (Figura 6a) indican que, para NPR 1.97 y NPR 2.94, el frente de onda de choque normal se encuentra dentro de la tobera. Para valores de NPR iguales o superiores a 3.92, el frente de choque se desplaza fuera de la tobera. En el caso de la tobera cónica, los campos de flujo del número de Mach (Figura 5b) y de presión estática (Figura 6b) muestran que, dentro del rango de NPR de 1.97 a 4.88, el frente de onda de choque normal permanece dentro de la tobera. Para valores de NPR iguales o superiores a 5.84, el frente de choque se desplaza fuera de la tobera.

La evolución del campo de flujo del número de Mach y del campo de presión estática para ambos sopladores, plano y cónico, demuestra que el régimen de flujo exhibe comportamientos distintos para el mismo valor de NPR. A medida que el NPR aumenta, la estructura de la onda de choque evoluciona y el punto de separación del flujo se desplaza más cerca de la salida del soplador.

En el soplador plano, la distribución de los choques internos es evidente tanto dentro del soplador como en el chorro supersónico que se descarga hacia la atmósfera. Sin embargo, para la misma magnitud de NPR, la distribución de los choques internos difiere en el soplador cónico. La intensidad del desplazamiento de la frente de choque es mayor en el soplador plano en comparación con el soplador cónico.

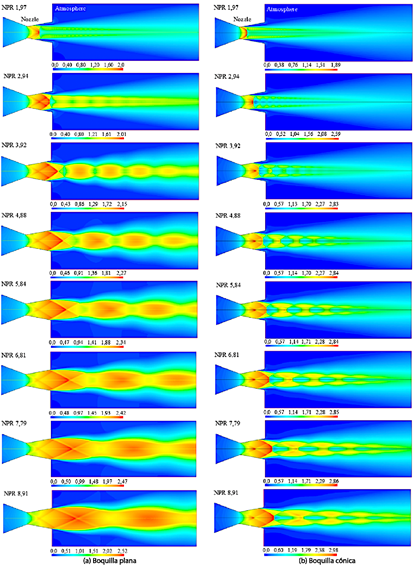
Figura 5 Patrones del campo de flujo del número de Mach. Rango: NPR 1,97 a NPR 8,91. (a) Soplador plano. (b) Soplador cónico. 

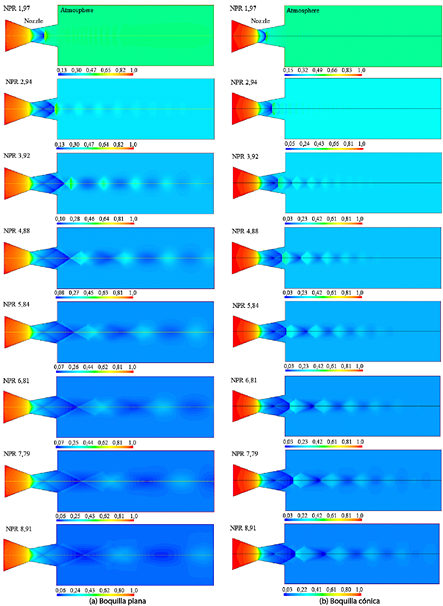
Figura 6 Patrones del campo de flujo de presión. Rango: NPR 1,97 a NPR 8,91. (a) Soplador plano. (b) Soplador cónico 

Las trayectorias de los perfiles de la línea central para los sopladores plano y cónico se ilustran en la Figura 7 para el número de Mach y en la Figura 8 para la presión estática.

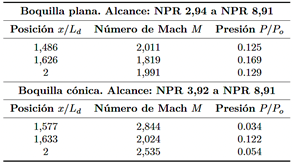
En la sección divergente (1 ≤ x/L_d ≤ 2) del soplador plano (Figura 7a y Figura 8a), se observan fluctuaciones de velocidad y presión estática para el rango de NPR de 2,94 a 8,91. La velocidad máxima de flujo ocurre en x/L_d = 1,486, donde el número de Mach alcanza 2,011, acompañado de una caída de presión de P/P_o = 0,125 (Tabla 2). En x/L_d = 1,626, el flujo se desacelera a Mach 1,819 con una caída de presión correspondiente de P/P_o = 0,169. En la salida del soplador, x/Ld = 2, la velocidad del flujo alcanza Mach 1,991 con una caída de presión de P/P_o = 0,129.

En contraste, dentro de la sección divergente (1 ≤ x/L_d ≤ 2) del soplador cónico (Figura 7b y Figura 8b), para el rango de NPR de 3,92 a 8,91, la velocidad máxima de flujo ocurre en x/L_d = 1,577, alcanzando Mach 2,844 con una caída de presión correspondiente de P/P_o = 0,034 (Tabla 2). La posición de este pico de velocidad máxima se desplaza un 6,12 % río abajo en comparación con la posición del pico en x/L_d = 1,486 en el soplador plano (Figura 7a). En x/L_d = 1,633, el flujo se desacelera a Mach 2,024 con una caída de presión de P/P_o = 0,122, mostrando un desplazamiento posicional del 0,43 %.

En la salida del soplador cónico (Figura 7b y Figura 8b), en la misma posición x/L_d = 2 que el soplador plano (Figura 7a y Figura 8a), el flujo alcanza Mach 2,535 con una caída de presión correspondiente de P/P_o = 0,054.

Esto representa un aumento del 27,32 % en la velocidad y una disminución del 58,13 % en la presión en comparación con el soplador plano. Se observa que en la salida del soplador cónico, se alcanza una mayor velocidad a lo largo de la línea central de la región central del flujo. Sin embargo, la tasa de flujo másico total es menor. Esta diferencia se atribuye al área de la garganta del soplador cónico A_t = 5,896 cm², que restringe el paso del flujo másico a velocidad sónica. Esta área de la garganta es un 78,79 % más pequeña que la del soplador plano A_t = 27,81 cm².

En la región atmosférica (2 ≤ x/Ld ≤ 8), el flujo de salida muestra fluctuaciones notables. Para el soplador plano (Figuras 7a y 8a), en NPR 8,91, la velocidad alcanza un pico máximo de Mach 2,522 con una caída de presión de P/Po = 0,056 en x/Ld = 2,95. Por el contrario, el soplador cónico (Figuras 7b y 8b) alcanza una velocidad máxima de Mach 2,976 con una caída de presión de P/Po = 0,027 en x/Ld = 2,408, lo que refleja un aumento aproximado del 18 % en la velocidad en esta posición. Más abajo, el soplador plano muestra fluctuaciones más suaves en la velocidad y la presión, mientras que estas fluctuaciones son más pronunciadas en el soplador cónico.

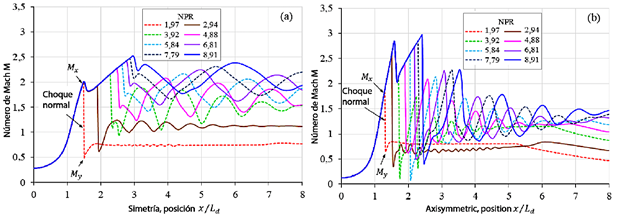
Figura 7 Patrones del perfil del número de Mach evaluados a lo largo de la línea central. (a) Soplador plano. (b) Soplador cónico. Posición: sección convergente (0 ≤ x/L_d ≤ 1), sección divergente (1 ≤ x/L_d ≤ 2) y sección atmosférica (2 ≤ x/L_d ≤ 8). 

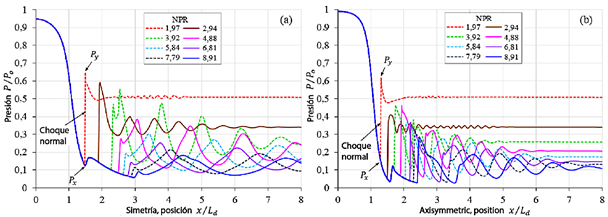
Figura 8 Patrones del perfil de presión evaluados a lo largo de la línea central. (a) Soplador plano. (b) Soplador cónico. Posición: sección convergente (0 ≤ x/L_d ≤ 1), sección divergente (1 ≤ x/L_d ≤ 2) y sección atmosférica (2 ≤ x/L_d ≤ 8). 

Tabla 2 Posición de las fluctuaciones máximas y mínimas en la región central del flujo supersónico a lo largo de la línea central de la sección divergente del soplador 

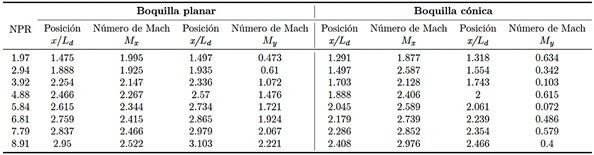
La Tabla 3 presenta las posiciones de la frente de choque normal evaluadas a lo largo de la línea central del soplador plano (Figura 7a) y del soplador cónico (Figura 7b). M_x representa la velocidad máxima de flujo al inicio de la frente de choque, mientras que M_y corresponde a la velocidad mínima de flujo al final de la misma. Las Figuras 7 y 8 también muestran la presión mínima P_x y la presión máxima P_y de la frente de choque para referencia.

En la sección divergente del soplador plano, se observan dos frentes de choque normales para los valores de NPR 1,97 y 2,94. Al inicio de los frentes de choque, el flujo alcanza velocidades supersónicas que van de Mach 1,995 a 1,925. Al final de los frentes de choque, el flujo pasa a velocidades subsónicas en el rango de Mach 0,473 a 0,610. Fuera del soplador, se identifican seis frentes de choque normales para los valores de NPR de 3,92, 4,88, 5,84, 6,81, 7,79 y 8,91. Al inicio de estos frentes de choque, el flujo exhibe velocidades supersónicas que van de Mach 2,147 a 2,522. Al final de los frentes de choque, el flujo transita a velocidades transónicas y supersónicas dentro del rango de Mach 1,072 a 2,221.

En la sección divergente del soplador cónico, se observan cuatro frentes de choque para los valores de NPR de 1,97, 2,94, 3,92 y 4,88. Al inicio de los frentes de choque, el flujo alcanza velocidades supersónicas que van de Mach 1,877 a 2,406. Al final de los frentes de choque, el flujo pasa a velocidades subsónicas en el rango de Mach 0,634 a 0,615. Fuera del soplador, se presentan cuatro frentes de choque adicionales para los valores de NPR de 5,84, 6,81, 7,79 y 8,91. Al inicio de estos frentes de choque, el flujo sigue siendo supersónico, con velocidades que van de Mach 2,589 a 2,976. Al final de los frentes de choque, el flujo pasa a velocidades subsónicas dentro del rango de Mach 0,072 a 0,4.

Se observa que, al inicio de los frentes de choque para valores de NPR iguales o superiores a 2,94, el flujo en el soplador cónico alcanza velocidades supersónicas más altas en comparación con el soplador plano. Al final del frente de choque, el flujo en el soplador cónico pasa a velocidad subsónica. En contraste, el flujo en el soplador plano muestra un rango más amplio de comportamientos al final del frente de choque, incluyendo velocidades subsónicas, transónicas y supersónicas.

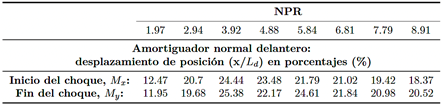
Los desplazamientos en las posiciones de los frentes de choque normales en el soplador cónico se resumen en la Tabla 3. Para el mismo valor de NPR, el frente de choque en el soplador cónico está desplazado más hacia la extrema izquierda en comparación con el frente de choque en el soplador plano. El menor desplazamiento de la posición del frente de choque ocurre en NPR 1,97, con el inicio del choque desplazado un 12,47 % y el final del choque un 11,95 %. Por el contrario, el mayor desplazamiento se observa en NPR 3,92, con el inicio del choque desplazado un 24,44 % y el final del choque un 25,38 %.

Tabla 3 Posiciones de los frentes de choque normales evaluados a lo largo de la línea central en la sección divergente (1 ≤ x/L_d ≤ 2) y la sección atmosférica (2 ≤ x/L_d ≤ 8). 

Hallazgos similares respecto al flujo sobreexpandido y las estructuras de choque divergente en sopladores planos han sido reportados en [6], [23], y en sopladores cónicos en [15], [27], donde los frentes de choque oblicuos, reflejados y normales son influenciados por la geometría de la pared y el ángulo de divergencia. Estos estudios demuestran que la geometría de los sopladores supersónicos impacta significativamente el desarrollo del régimen de flujo. Para las mismas dimensiones geométricas proyectadas en el plano, como se muestra en la Figura 2, el soplador plano y el soplador cónico exhiben áreas transversales distintas tanto en la garganta como en la salida del soplador [26]. El área transversal del soplador plano es mayor que la del soplador cónico, lo que ocasiona un menor flujo másico a través de la garganta del soplador cónico. Es importante señalar que los resultados numéricos están influenciados por las simplificaciones de los modelos matemáticos, la densidad de celdas en la malla computacional y los modelos de turbulencia empleados. En consecuencia, la validación con datos experimentales fue esencial. El modelo de turbulencia SAS, utilizado en las simulaciones, fue validado para asegurar que los resultados numéricos se aproximan estrechamente a los fenómenos físicos bajo investigación.

Tabla 4 Desplazamiento hacia la izquierda de las posiciones de los frentes de choque normales en el soplador cónico con respecto al soplador plano 

Conclusiones

Con base en los resultados obtenidos de las simulaciones computacionales del campo de flujo en sopladores planos y cónicos con un ángulo de divergencia α = 10,85°, clasificados como sopladores fuera de diseño, se pueden realizar las siguientes observaciones clave:

El comportamiento de los campos de flujo del número de Mach y la presión estática difiere notablemente entre los dos tipos de sopladores para el mismo valor de NPR. Dentro del rango de NPR de 1,97 a 8,91, las estructuras de onda de choque evolucionan de manera distinta, con sus posiciones y los puntos de separación del flujo, desplazándose progresivamente hacia la salida del soplador a medida que aumenta el NPR.

En la sección divergente del soplador plano, se observa que la velocidad máxima de flujo alcanza su pico en x/L_d = 1,486, alcanzando Mach 2,011 con una caída de presión de P/P_o = 0,125. En contraste, el soplador cónico alcanza su velocidad máxima de flujo en x/L_d = 1,577, con Mach 2,844 y una caída de presión correspondiente de P/P_o = 0,034. Esta posición está desplazada un 6,12 % hacia abajo en comparación con la posición x/L_d = 1,486 en el soplador plano.

En la región central del flujo, la velocidad en la salida del soplador difiere significativamente entre las dos geometrías. El soplador plano alcanza una velocidad de flujo de Mach 1,991, mientras que el soplador cónico alcanza Mach 2,535, lo que representa un aumento de velocidad del 27,32 % en relación con el soplador plano.

En la región atmosférica, en NPR 8,91, donde se forma el chorro supersónico, la velocidad máxima de flujo para el soplador plano es Mach 2,522. En comparación, el soplador cónico alcanza Mach 2,976, lo que refleja un aumento del 18 % en la velocidad de flujo. Estos hallazgos destacan el papel crítico del área de la garganta en la determinación del tránsito del flujo másico. El área de garganta más grande del soplador plano facilita un mayor flujo másico, mientras que el área de garganta más pequeña del soplador cónico restringe el flujo, lo que lleva a las diferencias observadas en los perfiles de velocidad y presión. Esto subraya el impacto significativo de la geometría del soplador en el comportamiento del flujo, especialmente en configuraciones fuera de diseño.