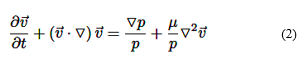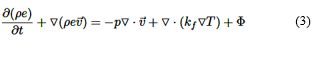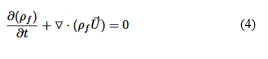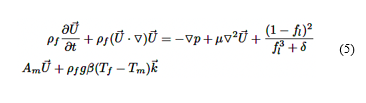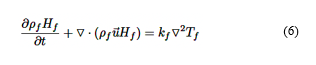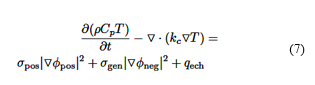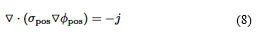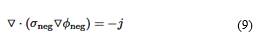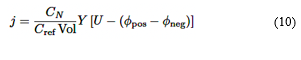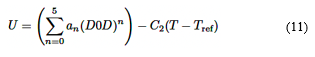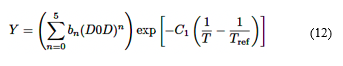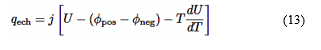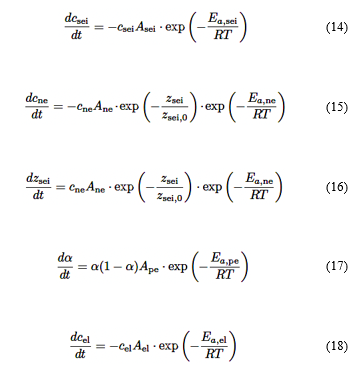Introducción
Las baterías de iones de litio (BIL) desempeñan un papel importante en numerosas aplicaciones, como dispositivos electrónicos portátiles, vehículos eléctricos, teléfonos inteligentes, dispositivos médicos, etc. Sin embargo, surgen grandes desafíos, como evitar su operación a temperaturas excesivas, lo cual puede ocasionar la fuga térmica, una reacción exotérmica descontrolada que puede provocar incendios, representando un riesgo para la seguridad humana y de los dispositivos [1].
Las BIL se han destacado como una fuente confiable de energía debido a su alta eficiencia, densidad de energía y vida útil relativamente larga [2]. Una celda de BIL consta de un terminal negativo (ánodo de grafito), un terminal positivo (cátodo, óxido metálico de litio), el separador y el electrolito. El separador está entre los electrodos para evitar el contacto eléctrico y permitir el paso de los iones. El material electrolítico se utiliza para facilitar la conducción iónica [3]. El proceso de carga/descarga de las baterías de iones de litio se caracteriza por la transferencia de iones de litio y electrones, lo que se denomina proceso de ionización y oxidación [4].
La operación de las BIL está condicionada por su temperatura, dado que, para un funcionamiento confiable y seguro, esta se encuentra entre los 15 °C a 35 °C [5]. En las celdas de litio existe una capa de material formada en la superficie de los electrodos durante el proceso de ciclado y uso, la misma que se denomina capa de interfase del electrolito (SEI, por sus siglas en inglés) y se descompone a 100 °C, mientras que el separador se funde y se contrae a 143 °C; sin embargo, a una temperatura superior a 150 °C, se produce el fenómeno conocido como fuga térmica [6-9].
Las baterías de iones de litio son más seguras desde su invención. Aunque existe un riesgo de incendio y explosión causado por la fuga térmica, al producirse el aumento exponencial de la temperatura a un ritmo que no se puede disipar lo suficientemente rápido al entorno, el calor causado por la descomposición química exotérmica de los materiales dentro de las celdas [10].
Para mantener la batería en un rango de temperatura adecuado, existen sistemas de refrigeración o enfriamiento, que según su medio se pueden clasificar en aire, líquido y material de cambio de fase (PCM) [11, 12].
Los sistemas de enfriamiento por aire se pueden clasificar en dos tipos: aire natural y aire forzado (mediante ventiladores) [13, 14].
Los sistemas de refrigeración de baterías por líquido pueden ser de forma directa o indirecta. La refrigeración directa se da cuando existe el contacto directo entre el refrigerante y las celdas de la batería. La refrigeración indirecta ocurre cuando se mantienen los paquetes de batería en un líquido refrigerante aislante, como aceites minerales y de silicona, que no reaccione químicamente con ninguno de los materiales en el exterior de las celdas [13].
En los sistemas de enfriamiento de PCM, se utilizan materiales que absorben o liberan cantidades de energía térmica en procesos de cambio de fase, que permitan un calentamiento o un enfriamiento [15].
Se han desarrollado varios estudios con los sistemas de enfriamiento de aire, agua y PCM, con el objetivo de prevenir la fuga térmica. Por ejemplo, Ouyang et al. [16] utilizaron cien baterías de litio tipo 18650 y demostraron que mediante el uso de aerogel de espesor 4 mm se puede reducir la temperatura máxima de la batería.
Zhou et al. [17] experimentaron un sistema de gestión térmica de baterías (BTMS) con tuberías de calor (heat pipes) y líquido de cambio de fase para controlar la temperatura y prevenir la propagación térmica. El sistema inhibe efectivamente el sobrecalentamiento y fuga térmica, manteniendo la temperatura por debajo de 185 °C y limitando la diferencia de temperatura a menos de 2.1 °C en condiciones de altas tasas de descarga.
Alghamdi et al. [18] llevaron a cabo un estudio experimental de diferentes sistemas de gestión térmica para BIL en vehículos eléctricos, centrándose en el uso de PCM. Los resultados muestran que cuando solo se usa PCM, la temperatura promedio alcanza 85 °C, superando el rango seguro. La adición de un módulo termoeléctrico y aletas de aluminio reduce la temperatura promedio a 48 °C, mejorando la seguridad del sistema.
Wu et al. [19] diseñaron un sistema de gestión térmica de baterías basado en PCM asistido por tubería de calor para vehículos eléctricos e híbridos. Los resultados experimentales muestran que las tuberías de calor influyen en la distribución de temperatura bajo altas tasas de descarga, manteniendo la temperatura máxima por debajo de 50 °C y logrando una fluctuación térmica más estable bajo condiciones cíclicas. Los autores demostraron que el aumento de la velocidad del aire reduce limitadamente la temperatura de las celdas debido al proceso de transición de fase del PCM.
Además, Liu et al. [20] simularon los comportamientos de la fuga térmica en un paquete de doce BIL prismáticas. Se evaluaron tres medidas de seguridad térmica para la protección contra cortocircuitos internos. Se propuso el uso de PCM de parafina para retrasar la propagación de la fuga térmica entre las baterías. Además, afirmaron que, adicionando aislamiento al PCM, este tiempo se puede extender. Complementariamente, se propone una protección térmica novedosa basada en refrigeración por inmersión con ebullición de líquido fluorinado.
Li et al. [21] propusieron un modelo numérico de abuso térmico con enfoque CFD, para estudiar la propagación térmica en un paquete de baterías de iones de litio. El modelo mostró que el espacio entre celdas acelera la transferencia de calor, pero reduce la densidad energética.
Se han realizado múltiples estudios para la simulación del acoplamiento electroquímico-térmico para baterías, que radica en el campo multiescala y multifísica. Para abordar esta dificultad, se ha empleado el método multidimensional multiescala (MSMD), que se encuentra implementado en ANSYS Fluent. El MSMD se resuelve en diferentes escalas y en varios dominios [22] y puede simular un paquete de baterías con sus celdas conectadas eléctricamente [23]. Además, se puede simular la fuga térmica de una batería bajo condiciones de abuso térmico y cortocircuito [24]. También Paccha-Herrara et al. [25] proponen el método MSMD junto con la implementación del modelo empírico NTGK, el cual permite calcular las propiedades térmicas y eléctricas para evaluar el desempeño térmico de las BIL.
En este estudio se analizarán estrategias que puedan prevenir la fuga térmica, con diferentes tipos de enfriamiento y disposiciones geométricas del modelo de celdas. La motivación principal de este estudio es evitar que las baterías de iones de litio lleguen a presentar el fenómeno de la fuga térmica al funcionar a temperaturas fuera del rango normal establecido, evitando posibles incendios o incluso que exploten. Este estudio aporta con propuestas de soluciones para la prevención de la fuga térmica, mediante la implementación de sistemas de enfriamiento en baterías de iones de litio, por medio de análisis y simulación con base en CFD. Se proponen distintas configuraciones geométricas de celdas, distintos sistemas de enfriamiento. De esta manera, se proponen sistemas de baterías de litio más seguros y eficientes.
Materiales y métodos
Para la ejecución del presente trabajo, se utilizaron tres disposiciones geométricas de las celdas con diferentes sistemas de enfriamiento. La simulación numérica se implementará en el paquete computacional ANSYS STUDENT 2024 R1, mediante modelos CFD.
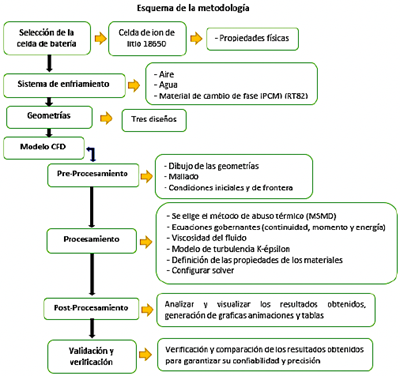
En la Figura 1 se muestra una representación esquemática del procedimiento empleado para efectuar este estudio sobre las estrategias de enfriamiento para la prevención de la fuga térmica. Se inicia por la selección de la celda y sistemas de enfriamiento. A continuación, se desarrollan las geometrías y el mallado. Luego, se seleccionan los modelos CFD, configurando materiales, condiciones iniciales y de frontera y solver numérico. Finalmente, se realiza el análisis formal de resultados.
Resolución numérica
Las ecuaciones gobernantes que se resuelven en la simulación CFD para el dominio de aire y agua son las ecuaciones de continuidad, momento y energía. Se ha considerado condiciones de flujo incompresible, donde la densidad del fluido es constante. La ecuación de continuidad se observa en la ecuación (1) [26]:
Donde ▽ es el operador de divergencia y v es la velocidad del fluido.
La ecuación (2) representa la conservación del momento para un fluido incompresible y viscoso:
La ecuación (3) muestra la forma de conservación de la energía para un fluido:
Donde 𝑣 es la velocidad del fluido, p es la presión, ρ es la densidad del aire, μ es la viscosidad dinámica, e es la energía interna, T es la temperatura, kf es la conductividad térmica del fluido, Φ la disipación viscosa y t es el tiempo.
Para modelar los efectos de turbulencia, se empleó el modelo k − épsilon debido a su robustez [27].
Para el caso del PCMRT82, dado que existe cambio de fase, se utilizan las ecuaciones de continuidad (ecuación (4)), momento (ecuación (5)) y energía (ecuación (6)) [28].
Donde 𝜕 ρ 𝑓 𝜕𝑡 es la tasa de cambio temporal de la densidad, ρf es la densidad en fase de fluido, 𝑈 es el vector de velocidad del fluido (con componentes 𝑢 , 𝑣 , y 𝑤 ).
Donde β es el número consecutivo en la región de transición (mushy region), Am es un parámetro para la región de transición, δ es una cantidad pequeña para evitar que el término se divida por cero, y fl es la fracción líquida.
Donde Hf es la entalpía de fluido.
Modelo NTGK
Para modelar el fenómeno de la fuga térmica se ha empleado el modelado multidominio multiescala (MSMD), basado en el modelo empírico NTGK/DCIR.
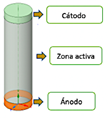
El modelo NTGK, mediante las ecuaciones (7), (8) y (9), permite calcular las propiedades termoeléctricas del dominio del ánodo, cátodo y zona activa de una celda o banco de baterías que pueden estar conectadas eléctricamente [25]:
Donde kc es la conductividad térmica, σ es la conductividad eléctrica, ϕ es el potencial eléctrico, qech es la tasa de transferencia de calor debido al intercambio térmico con el entorno, y los subíndices pos y neg se refieren al electrodo positivo y negativo, respectivamente. La tasa de corriente volumétrica j se formula mediante la ecuación (10) [29]:
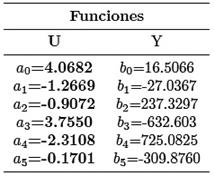
Donde Vol es el volumen de la zona activa, Cref capacidad de la batería utilizada para obtener los parámetros de las funciones U y Y, las cuales están dadas por las ecuaciones (11) y (12), respectivamente [29] y sus coeficientes se muestran en la Tabla 1.
Donde C2 y C1 son constantes para una batería específica.
La tasa de transferencia de calor debido al intercambio térmico con el entorno qech se describe como se ve en la ecuación (13) [25]:
Donde el primer término representa el calor sobrepotencial y el segundo término es el componente entrópico.
Modelo de abuso térmico
El modelo de abuso térmico fue propuesto por primera vez por Harchard et al. [30], luego fue ampliado por Kim et al. [31]. Este modelo se formula con base en la ecuación de Arrhenius y abarca un sistema de ecuaciones que describen las reacciones durante la descomposición del electrodo positivo, el electrodo negativo y el SEI (interfase sólido-electrolito), tal como se describe a continuación:
Donde los subíndices ne, np y el representaran la reacción entre el electrodo negativo y el electrolito, la reacción entre el electrodo positivo y el electrolito, y la reacción de descomposición del electrolito, respectivamente. Además, zsei es una medida adimensional del grosor de la capa SEI; z(sei,0) es el grosor de referencia de la capa SEI; csei es la fracción de la concentración de especies metaestables que contienen litio en la capa SEI; cne es la fracción de la concentración de litio en el electrodo negativo; α representa el grado de conversión del cátodo y cel es la concentración del electrolito. Todas estas variables son adimensionales. R es la constante universal de los gases.
Selección de la celda de batería
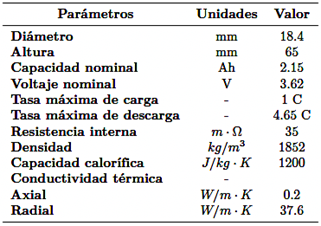
En este estudio se utilizaron celdas cilíndricas de iones de litio de tipo 18650. Las propiedades se muestran en la Tabla 2.
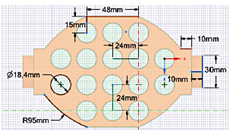
En la Figura 2 se muestran las partes principales de una batería de iones de litio 18650 empleada en el presente estudio, que dispone de un diámetro de 18.4 mm, una altura del ánodo de 2 mm, el cátodo de 3 mm y la zona activa de 60 mm.
Sistemas de enfriamiento
Los sistemas de enfriamiento propuestos en este trabajo son aire, agua y PCM. Para el caso del PCM, se utilizará el RT82, compuesto por materiales orgánicos puros que puede almacenar y liberar grandes cantidades de calor y utiliza un proceso de fusión de sólido a líquido o viceversa [32]. Las propiedades del PCM RT82 se presentan en la Tabla 3.
Disposiciones geométricas de las celdas
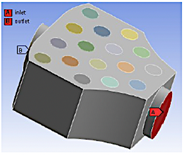
Las geometrías utilizadas para el estudio se realizaron en el módulo Ansys SpaceClaim de ANSYS Fluent.
Se propuso tres geometrías con dieciséis celdas de iones de litio 18650 con diferentes disposiciones, utilizando tres métodos de enfriamiento: aire, agua y PCM RT82. Para el análisis de la fuga térmica en las celdas se empleó el modelo de abuso térmico (thermal abuse model) de ANSYS Fluent, basado en el método MSMD con la implementación del modelo empírico NTGK.
Se establece la temperatura ambiente y de entrada de fluidos en 25 °C, con un coeficiente de convección entre la carcasa y el ambiente externo de 7 W m 2 K , como lo recomienda Liu et al. [20], una velocidad de entrada tanto para el aire como para el agua de 1.5 m s . El criterio de convergencia en este estudio fue cuando los residuos alcanzaron valores inferiores a 1×10−04. Para cada caso, se utilizó una caja acrílica para encerrar las baterías. Las dieciséis celdas se conectaron en serie empleando la conexión virtual del MSMD de Fluent y el tamaño del paso del tiempo (time step size) fue de 1 s. El material empleado para simular el ánodo y cátodo fue el aluminio.
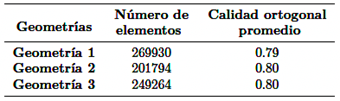
Se utilizó un mallado estructural de tipo hexaédrico buscando un balance entre precisión y eficiencia computacional, se realizó una prueba de independencia de mallas con tres tamaños de elementos para cada geometría, escogiendo la que mantuvo la temperatura constante al incrementar el número de elementos. El número de elementos para las distintas geometrías y el promedio de la calidad ortogonal se muestran en la Tabla 4. Los indicadores de este último parámetro evidencian que la calidad del mallado es muy buena.
Para el caso de la convección natural, se aplicó el método PRESTO! para la discretización de la presión, mientras que para el acoplamiento presión-velocidad se empleó un esquema COUPLED.
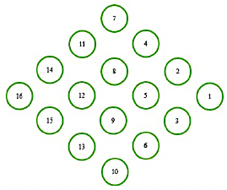
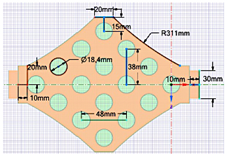
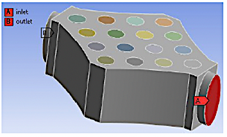
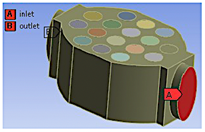
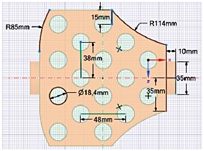
La geometría 1 tiene una forma de rombo irregular (Figura 3) con una separación entre filas de 48 mm y entre columnas de 38 mm. La geometría 2 es de forma de octagonal irregular (Figura 6) con una separación entre filas de 24 mm y entre columnas de 24 mm. La geometría 3 tiene una forma de un octágono irregular (Figura 9) con una separación entre filas de 38 mm y entre columnas de 48 mm.
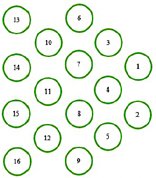
En las figuras 3, 4 y 5 se exponen el orden enumerado de las celdas, la configuración de los espacios entre celdas y carcasa y la dirección del flujo de refrigerante para la geometría 1, respectivamente. En las figuras 6, 7 y 8 se exhiben similares características para la geometría 2. En las figuras 9, 10 y 11 se muestran detalles análogos para la geometría 3.
Este estudio se realizó utilizando un computador tipo laptop con procesador Ryzen 7, 7.8 GHz, 16 GB RAM.
Resultados y discusión
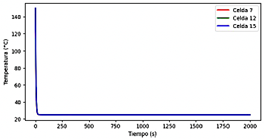
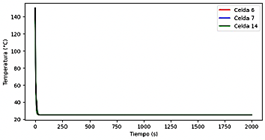
La Figura 12 muestra una gráfica típica del enfriamiento de una celda por medio de aire, donde al final del proceso se alcanza el estado estable.
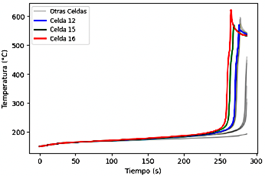
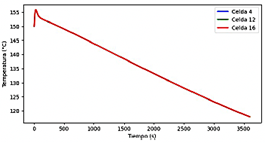
Un patrón típico de la fuga térmica se expone en la gráfica 13, donde, luego del tiempo 505 s, un pequeño aumento de temperatura lleva a una reacción en cadena descontrolada que incrementa exponencialmente la temperatura del sistema. Esto es un fenómeno crítico, especialmente en baterías de litio, lo cual puede implicar fallos catastróficos si no se controla adecuadamente.
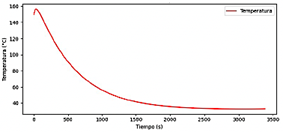
Figura 12 Dinámica de enfriamiento de una batería. Enfriado por aire con convección forzada, temperatura ambiente y de entrada de 25 °C, y velocidad de entrada de 1.5 m/s
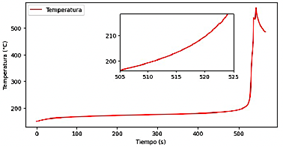
Figura 13 Perfil de temperatura característico de la fuga térmica en una celda. Enfriamiento por aire, con temperatura de entrada al módulo de 47 °C y velocidad 1.5 m/s
Enfriamiento por aire
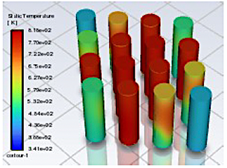
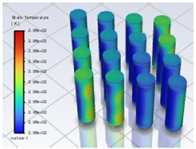
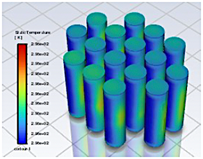
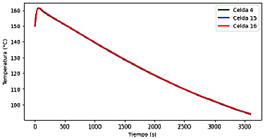
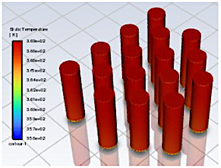
En la Figura 14 se muestran los perfiles de temperatura de las celdas para la geometría 1, utilizando enfriamiento por aire mediante convección natural, la cual no evita la fuga térmica, siendo la celda 16, en un tiempo de 258 s, primera en sufrir dicho fenómeno. En la Figura 15 se expone la distribución de la temperatura en las celdas.
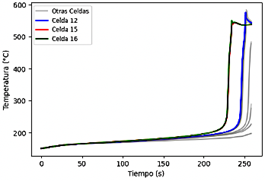
En la Figura 16 se presentan los resultados para la geometría 2, con enfriamiento por aire mediante convección natural, la cual no evita la fuga térmica, siendo las celdas 15 y 16 las primeras en presentar dicha condición anómala luego de un período de 228 s. La distribución de la temperatura en las celdas se presenta en la Figura 17.
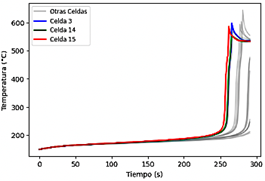
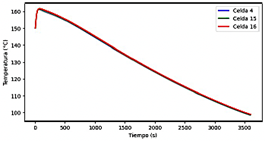
En la Figura 18 se muestran las temperaturas de las baterías para la geometría 3, utilizando enfriamiento por aire mediante convección natural, siendo la celda 15 la primera en experimentar la fuga térmica luego de un tiempo de 255 s. La distribución de la temperatura en las celdas se aprecia con más detalle en la Figura 19, en donde las celdas centrales sufren los mayores incrementos de temperatura.
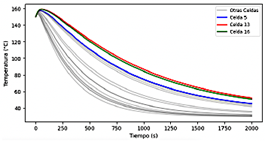
En la Figura 20 se observan las curvas de temperatura para la geometría 1, utilizando enfriamiento por aire mediante convección forzada, lo cual previno la fuga térmica, siendo la celda 5 la que alcanzó la temperatura más alta de 156.98 °C, en un tiempo de 35 s. En la Figura 21 se presenta la distribución de la temperatura en las celdas, en donde existen celdas localizadas en extremos que no se refrigeran adecuadamente.
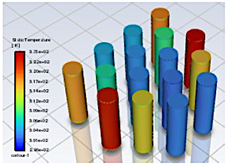
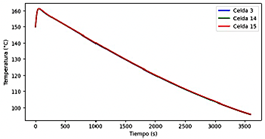
En la Figura 22 se exhiben los resultados de evolución de temperatura de las celdas para la geometría 2, utilizando enfriamiento por aire mediante convección forzada, lo cual inhibió la fuga térmica, siendo la celda 3 la que alcanzó la temperatura más alta que es 157.30 °C en un tiempo de 33 s. En la Figura 23 se muestra la distribución de la temperatura en el módulo, anotando que las celdas localizadas cerca de la entrada de aire se refrigeran de mejor manera con respecto a las ubicadas cerca de la salida de aire.
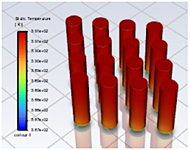
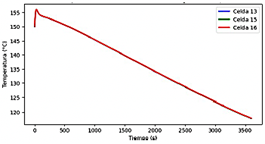
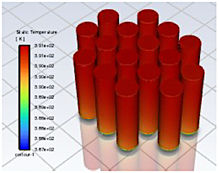
En la Figura 24 se observa la geometría 3, utilizando enfriamiento por aire mediante convección forzada, lo cual previno la fuga térmica, pero existe un mayor gradiente de temperatura entre las celdas vecinas con respecto a la geometría 2. La celda 13 alcanzó la temperatura más alta que es de 159.31 °C en un tiempo de 56 s. La Figura 25 presenta la distribución de la temperatura en las celdas, en donde las celdas de la zona central del módulo presentan una mejor refrigeración.
Enfriamiento por agua
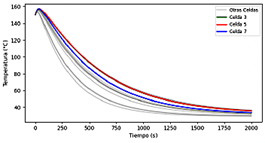
La Figura 26 evidencia un decaimiento de temperatura de las celdas para la geometría 1, inhibiendo la fuga térmica por medio de enfriamiento por agua mediante convección natural. La celda 16 alcanzó la temperatura más alta correspondiente a 155.90 °C en un tiempo de 27 s. En la Figura 27 se muestra la distribución de la temperatura en las celdas, en donde se evidencia que la temperatura es prácticamente uniforme.
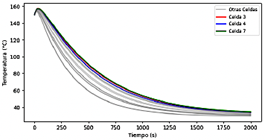
El comportamiento térmico de las celdas correspondiente a la geometría 2 se ve en la Figura 28. Se empleó el enfriamiento por agua mediante convección natural, lo cual previno la fuga térmica. La celda 16 alcanzó la temperatura más alta de 156.09 °C en un tiempo de 29 s. En la Figura 29 se presenta la distribución de la temperatura en las celdas, que se muestra uniforme.
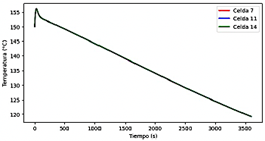
En la Figura 30 se presentan los resultados para la geometría 3, utilizando enfriamiento por agua mediante convección natural. La celda 7 alcanzó la temperatura más alta, que es 156.19 °C en un tiempo de 29 s y no se experimentó fuga térmica. En la Figura 31 se muestra la distribución uniforme de la temperatura en las baterías.
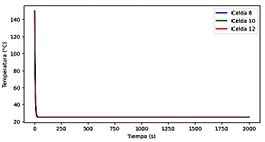
En la Figura 32 se ven las temperaturas de algunas celdas para la geometría 1, empleando enfriamiento por agua mediante convección forzada. Todas las celdas alcanzan el estadio estacionario, inhibiendo la fuga térmica. En la Figura 33 se ve una distribución uniforme de la temperatura en las celdas.
En la Figura 34 se observan las temperaturas de las celdas para la geometría 2. Se empleó el enfriamiento por agua mediante convección forzada, lo cual evitó la fuga térmica, conduciendo a un estado estacionario. En la Figura 35 se presenta la distribución de la temperatura en las celdas con un patrón uniforme.
En la Figura 36 se muestran los resultados para la geometría 3, empleando enfriamiento por agua mediante convección forzada. En este caso, también se inhibe la fuga térmica alcanzando el estado estable. En la Figura 37 está la distribución de la temperatura en las celdas, en donde los gradientes son despreciables.
Enfriamiento por PCM (RT82)
En la Figura 38 se expone el comportamiento térmico de la geometría 1, utilizando enfriamiento por PCM (RT82), lo cual previno la fuga térmica. La celda 16 alcanzó la temperatura más alta que fue de 161.40 °C en un tiempo de 61 s y luego se existe un decaimiento. En la Figura 39 se observa una distribución uniforme de la temperatura en las celdas.
En la Figura 40 se presentan las temperaturas de las celdas para la geometría 2, empleando enfriamiento por PCM (RT82). En este caso también se evitó la fuga térmica, siendo las celdas 15 y 16 las que alcanzaron la temperatura más alta, que es 161.71 °C en un tiempo de 74 s. En la Figura 41 se muestra la distribución de la temperatura en las celdas, que también exhiben un patrón uniforme.
En la Figura 42 se muestran los resultados de la geometría 3, utilizando enfriamiento por PCM. La celda 15 alcanzó la temperatura más alta que es 161.46 °C en un tiempo de 59 s y luego también se produjo un decaimiento de temperatura. En la Figura 43 se muestra que la distribución de la temperatura en las celdas sigue siendo uniforme, de manera similar para las otras configuraciones geométricas con PCM.
El fenómeno de la fuga térmica tiene gran impacto al momento de elegir el sistema de enfriamiento y disposición geométrica de las celdas de las baterías, ya que de estos parámetros depende su inhibición. Por eso se han hecho varios estudios como Zhou et al. [17], que consiguieron prevenir la propagación de la fuga térmica, logrando permanecer por debajo de 185 °C y por encima de 60 °C durante solo 14 s. También Ouyang et al. [16] lograron reducir la temperatura máxima de las baterías de tipo 18650 desde 740.35 °C a 55.19 °C, previniendo la fuga térmica, mientras que en el estudio de Alghamdi et al. [18], utilizando PCM de parafina, se alcanzó una temperatura media de 85 °C.
Conclusiones
Se llevó a cabo un estudio numérico para la refrigeración de celdas en un módulo de baterías refrigerado por aire, agua y PCM. Se propusieron tres diferentes configuraciones geométricas del módulo de baterías para estudiar la inhibición de la fuga térmica.
De las geometrías analizadas, en el caso de enfriamiento por convección natural por aire las tres configuraciones geométricas no evitaron la fuga térmica. Cuando se utilizó agua y PCM RT82 sí se logró evitar el fenómeno. Al emplear agua, la más eficiente es la geometría 1, alcanzando una temperatura máxima de 155.90 °C. Al usar PCM RT82, la más eficiente es la geometría 1, logrando una temperatura máxima de 161.40 °C.
Utilizando convección forzada por aire, la configuración más eficiente fue la geometría 1, obteniendo una temperatura máxima de 156.98 °C, mientras que, empleando enfriamiento por agua, la más eficiente también fue la geometría 1, logrando reducir la temperatura de 150 °C a 25.06 °C.
Con los resultados obtenidos se puede establecer que la geometría 1 es la más eficiente.
De los tres sistemas de enfriamiento utilizados en el estudio, el más eficiente en prevenir la fuga térmica es el agua, debido a la alta capacidad calorífica y alta conductividad térmica, permitiendo una distribución eficiente del calor y su posterior disipación.
Una de las limitaciones de este estudio es el uso de un número limitado de celdas por lo que se sugiere como trabajo futuro poner en marcha modelos con otras disposiciones geometrías adicionales y número de celdas. Además, se sugiere evaluar el contacto indirecto entre celdas y refrigerante, así como otros tipos de PCM. Este estudio ayuda a comprender mejor el fenómeno de la fuga térmica y, de esta manera, instrumentar el sistema de enfriamiento más adecuado para evitarlo.