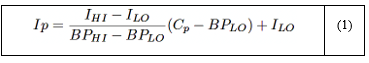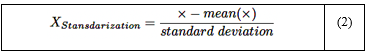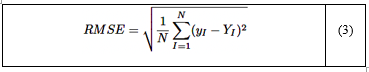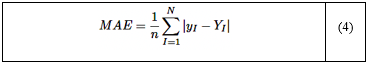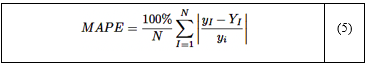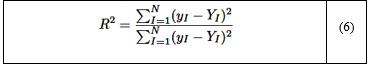Introducción
La contaminación del aire representa un desafío significativo para el desarrollo sostenible debido a su profundo impacto en la salud pública, siendo responsable de aproximadamente siete millones de muertes en el mundo en 2019, según la Organización Mundial de la Salud (OMS) [1,2]. A pesar de los beneficios para la salud que ofrece un aire limpio, una parte considerable de la población reside en áreas urbanas o cerca de instalaciones industriales con altos niveles de emisiones vehiculares [3]. La combustión de combustibles fósiles libera contaminantes nocivos, incluidos monóxido de carbono (CO), ozono (O3), dióxido de azufre (SO2), dióxido de nitrógeno (NO2) y material particulado (PM2.5 and PM10), los cuales afectan negativamente la salud humana y el medioambiente. [4]. El índice de calidad del aire (ICA) es una métrica crucial para evaluar y gestionar la calidad del aire, proporcionando una medida integral para analizar los niveles de contaminación y sus implicaciones [5, 6].
El ICA ha sido ampliamente estudiado por sus impactos ambientales [7-9], implicaciones económicas [7], [10] y aplicaciones predictivas utilizando datos de estaciones de monitoreo [11-13]. Los métodos para su predicción se clasifican generalmente en modelos numéricos y modelos basados en datos [14]. Los enfoques estadísticos tradicionales, como la regresión lineal [15,16], se emplean junto con algoritmos de aprendizaje automático (AA) [17, 18] y modelos híbridos que integran elementos de ambas metodologías [14], [19]. Desde principios del siglo XXI, las técnicas de AA, incluyendo redes neuronales artificiales (ANN), máquinas de soporte vectorial (SVM), máquinas de aprendizaje extremo (ELM) y k-vecinos más cercanos (KNN), han predominado en la predicción del ICA [20, 21]. A pesar de su uso generalizado, estos métodos presentan limitaciones en el procesamiento de datos temporales, lo que ha llevado a la adopción de redes neuronales recurrentes (RNN), como Long Short-Term Memory (LSTM) y Gated Recurrent Unit (GRU), para tareas de predicción de secuencias.
Investigaciones recientes han demostrado la eficacia de las redes neuronales convolucionales (CNN) en la predicción del ICA. Por ejemplo, Yan et al. [22] desarrollaron modelos que utilizan arquitecturas CNN, LSTM y CNN-LSTM, concluyendo que LSTM ofrece un rendimiento óptimo para pronósticos de varias horas, mientras que CNN-LSTM es más adecuado para predicciones a corto plazo.
De manera similar, Hossain et al. [23] integraron GRU y LSTM para la predicción del ICA en Bangladés, logrando un rendimiento superior en comparación con técnicas individuales. Para abordar las dependencias a largo plazo en datos secuenciales, el modelo Transformer, que emplea una arquitectura encoder-decoder, ha emergido como una solución prometedora [24].
Guo et al. [25] aplicaron una red basada en Transformer, BERT, para la predicción del ICA en Shanxi, China, alcanzando una precisión superior en comparación con LSTM. Ma et al. [26] desarrollaron el modelo Informer para la predicción del ICA en Yan’an, China, demostrando mejoras notables en fiabilidad y precisión. Además, Xie et al. [27] propusieron un modelo Transformer de entradas múltiples en paralelo para la predicción del ICA en Shanghái.
La comparación de modelos de IA para la predicción del ICA es fundamental debido a las variaciones en bases de datos, métricas de evaluación y algoritmos, que influyen significativamente en el desempeño de los modelos. Identificar el modelo más efectivo es esencial para mejorar la precisión de las predicciones y respaldar decisiones informadas en la gestión de la calidad del aire, un factor clave en la salud pública y la planificación urbana.
Materiales y métodos
Descripción general
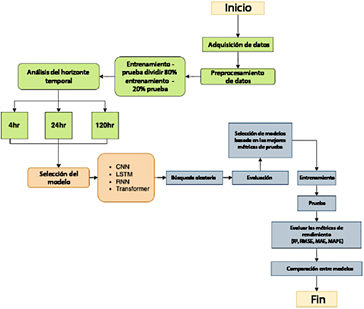
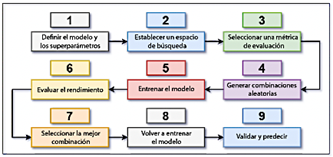
La metodología de esta investigación consta de los siguientes pasos, como se ilustra en la Figura 1:
Adquisición y preprocesamiento de datos.
División de los datos en subconjuntos de entrenamiento (80 %) y prueba (20 %).
Análisis del horizonte temporal con opciones establecidas en 4, 24 y 120 horas.
Selección de modelos: arquitecturas CNN, LSTM, RNN y Transformer.
Aplicación de una búsqueda aleatoria para la selección óptima de hiperparámetros.
Evaluación de los modelos utilizando las mejores
métricas de las pruebas.
Entrenamiento de los modelos seleccionados con los mejores hiperparámetros.
Pruebas de los modelos entrenados.
Evaluación del desempeño de los modelos utilizando R2, RMSE, MAE y MAPE.
Comparación de resultados entre los modelos.
Elaboración de conclusiones basadas en la comparación de modelos y el análisis general.
Caso de estudio
Los datos de series temporales utilizados en este estudio fueron obtenidos de una estación meteorológica en Cuenca, Azuay, Ecuador, ubicada en la calle Bolívar 7-77 y Antonio Borrero (coordenadas: latitud -2.897, longitud -79.00). Gestionada por la Empresa Municipal de Movilidad, Tránsito de Transporte de la Municipalidad de Cuenca (EMOV-EP), esta estación proporciona datos disponibles públicamente para uso personal, de investigación y gubernamental. Ubicada en una zona céntrica caracterizada por su importancia comercial, turística, colonial y residencial, esta estación forma parte de una red de tres estaciones de monitoreo en Cuenca, como se muestra en la Figura 2.
Preprocesamiento de datos
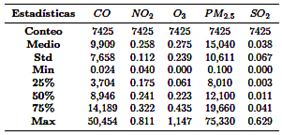
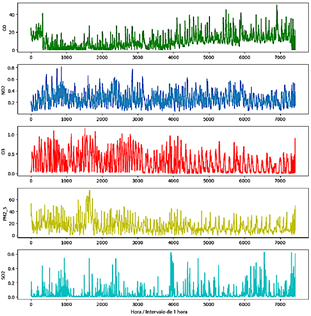
La estación meteorológica registró emisiones de gases, incluyendo CO,NO2,O3, PM2.5, and SO2, a intervalos de 10 minutos a lo largo de 2022, generando aproximadamente 52 560 registros. Estos fueron exportados en formato CSV desde el sitio web oficial de EMOVEP. Donde fue necesario, se convirtieron las unidades de medida de los contaminantes (por ejemplo, mg/m3 de CO a ppm) para facilitar el cálculo del ICA. Se calcularon los promedios horarios, reduciendo el conjunto de datos a 8760 registros. Después de filtrar los valores nulos y los datos irrelevantes, se retuvieron 7425 registros para el análisis. La Tabla 1 proporciona una visión general de los datos de la serie temporal, mientras que la Figura 3 ilustra la variación horaria de los gases registrados.
Usando los valores filtrados, se calculó el ICA para cada contaminante siguiendo las directrices establecidas en el informe de calidad del aire publicado por la Agencia de Protección Ambiental de los EE. UU. [28]. Su cálculo se basa en la concentración del contaminante y se determina utilizando la ecuación (1).
Donde:
IP es el índice de contaminante p.
CP es la concentración redondeada del contaminante p.
BPHI es el punto de corte que es mayor o igual a CP .
BPLO es el punto de corte que es menor o igual a CP.
IHI es el valor del ICA correspondiente a BPHI .
ILO es el valor del ICA correspondiente a BPLO.
Los valores individuales del índice de contaminante (Ip) para cada contaminante p se calculan de manera independiente, y el ICA final se determina seleccionando el valor máximo del conjunto de índices calculados. Esta metodología de selección garantiza que el ICA final refleje el contaminante que presenta el mayor potencial de impactos adversos en la salud, proporcionando una evaluación integral de las condiciones de calidad del aire.
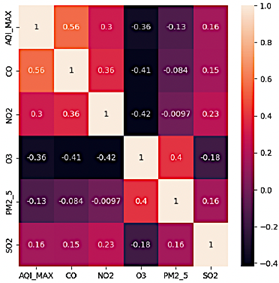
Para analizar la relación entre los contaminantes y el ICA calculado, se construyó una matriz de correlación, como se ilustra en la Figura 4.
La Figura 4 ilustra que, en este caso específico, basándose únicamente en los datos de contaminantes registrados por la estación meteorológica, el valor del ICA muestra una correlación más fuerte con CO y NO2, mientras que su correlación con O3, PM2.5 y SO2 es mínima. Esta información será considerada para el desarrollo y la configuración de los modelos de IA en análisis posteriores.
La estandarización implica transformar los datos, de manera que tengan una media de 0 y una desviación estándar de 1. Este proceso se representa analíticamente mediante la ecuación (2), que fue utilizada en esta investigación:
Donde:
X: Es el valor requerido para ser normalizado.
Media: La media aritmética de la distribución.
Desviación estándar: Desviación estándar de la distribución.
Finalmente, después de estandarizar los valores de la serie temporal, el conjunto de datos se dividió, asignando el 80 % para el entrenamiento y el 20 % reservado para las pruebas.
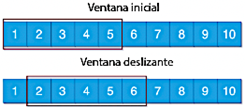
Ventana deslizante
Hota et al. [29] destacan que una técnica comúnmente utilizada en el análisis de series temporales es la creación de ventanas deslizantes, que proporciona una aproximación temporal del valor verdadero de los datos de la serie temporal. Este método acumula datos históricos de la serie temporal dentro de una ventana especificada para predecir el valor subsecuente. La Figura 5 ilustra el proceso de la ventana deslizante con un tamaño de ventana de 5.
Considerando el enfoque mencionado, se utilizaron ventanas deslizantes de 4, 24 y 120 horas para predecir intervalos de tiempo subsecuentes.
Aprendizaje profundo
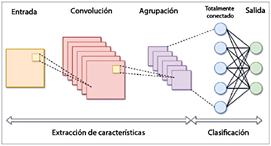
Redes neuronales convolucionales (CNN), redes neuronales recurrentes (RNN), memoria a largo corto plazo (LSTM), modelo Transformer
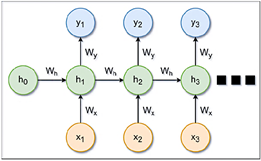
Las redes neuronales recurrentes (RNN) son una clase de redes neuronales diseñadas específicamente para procesar datos secuenciales. Su arquitectura permite que la salida de una capa se retroalimente en la entrada, lo que permite a la red retener la memoria de los estados anteriores. Esta capacidad hace que las RNN sean particularmente efectivas para tareas que requieren información contextual o histórica, incluyendo la predicción de series temporales, el procesamiento del lenguaje natural y el reconocimiento de voz [30]. Una configuración estándar de RNN se ilustra en la Figura 7.
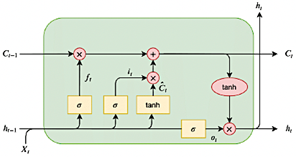
Las redes de memoria a largo corto plazo (LSTM) se desarrollaron para abordar las limitaciones de las RNN tradicionales, como el problema del gradiente desvanecido, mediante la incorporación de una celda de memoria capaz de retener información durante períodos prolongados [31]. Cada celda LSTM consta de tres puertas: la de entrada, que controla la incorporación de nueva información; la de olvido, que elimina los datos irrelevantes; y la de salida, que determina la información que se pasará al siguiente paso [31]. Una configuración estándar de LSTM se muestra en la Figura 8.
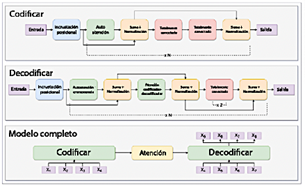
Los Transformers han atraído considerable atención por su destacado comportamiento en diversos dominios, incluyendo el procesamiento de lenguaje natural (NLP), la visión por computadora y el procesamiento de voz. Reconocidos por su capacidad para modelar dependencias a largo plazo e interacciones complejas en datos secuenciales, los Transformers son particularmente adecuados para tareas de predicción de series temporales [24]. La arquitectura instalada en este estudio se muestra en la Figura 9.
Métricas de rendimiento
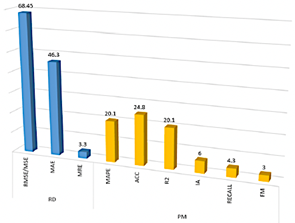
La investigación realizada por Méndez et al. [20] tuvo como objetivo identificar los principales factores que influyen en la predicción de la calidad del aire durante el período 2011-2021. Los autores encontraron que las métricas más comúnmente aplicadas para evaluar modelos de aprendizaje automático (ML) incluyen RMSE, MAE, MAPE, ACC y R2, como se ilustra en la Figura 10.
Error cuadrático medio (RMSE)
El error cuadrático medio (RMSE) es una métrica ampliamente utilizada que cuantifica la diferencia promedio entre los valores predichos y observados [34]. La fórmula para el RMSE se presenta en la ecuación (3):
Donde:
n: número de muestras.
yI: valor observado.
yI: valor predicho.
(yI−YI)2: error cuadrado entre los valores predichosy observados.
Error absoluto medio (MAE)
El error absoluto medio (MAE) es una métrica utilizada para evaluar la precisión de un modelo calculando el promedio de los errores absolutos entre los valores predichos y observados [34]. La fórmula para el MAE se presenta en la ecuación (4):
Donde:
n: número de muestras.
yI: valor observado.
yI: valor predicho.
|yI − YI|: error absoluto entre los valores predichos y observados.
Error absoluto porcentual medio (MAPE)
El error absoluto porcentual medio (MAPE) cuantifica el error promedio como un porcentaje de los valores observados, proporcionando una métrica independiente de la escala que facilita las comparaciones entre diferentes modelos [34]. La fórmula para el MAPE se presenta en la ecuación (5):
Donde:
n: número de muestras.
yI: valor observado.
yI: valor predicho.
Coeficiente de determinación (R 2 )
El coeficiente de determinación (R2) cuantifica la proporción de la varianza en la variable dependiente que es explicada por las variables independientes del modelo. Un valor de R2 de 1 indica que el modelo explica perfectamente la variabilidad de los datos, mientras que un valor de 0 significa que el modelo no explica ninguna variabilidad [34]. La fórmula para R2 se presenta en la ecuación (6):
Donde:
n: número de muestras.
yI: valor observado.
yI: valor predicho.
y: media de todos los valores observados yI .
Búsqueda aleatoria
En aprendizaje automático (ML), la búsqueda aleatoria (RS) es una técnica de optimización utilizada para identificar los hiperparámetros óptimos mediante la exploración de combinaciones aleatorias dentro de un espacio de parámetros predefinido. Este enfoque es más eficiente y computacionalmente menos costoso en comparación con los métodos de búsqueda exhaustiva [35]. La Figura 11 ilustra la secuencia de pasos involucrados en el proceso de RS.
El proceso implica los siguientes pasos:
Identificar el modelo de IA a optimizar y definir sus hiperparámetros.
Establecer los rangos para cada hiperparámetro.
Especificar las métricas de evaluación, como R2, MAE y RMSE.
Seleccionar aleatoriamente combinaciones de hiperparámetros.
Entrenar el modelo y evaluar su rendimiento.
Elegir la combinación con mejor rendimiento y volver a entrenar el modelo.
Validar el rendimiento del modelo optimizado.
Resultados y discusión
Análisis de correlación
La Figura 4 ilustra la relación entre las variables utilizando el coeficiente de correlación de Pearson para evaluar su correlación con la concentración máxima de ICA (ICAMAX). El mapa de calor revela que CO tiene la correlación positiva más fuerte con ICAMAX (0.56), seguido por NO2 (0.3) y SO2 (0.16), mientras que O3 muestra una correlación negativa (-0.36). Además, CO está moderadamente correlacionado con NO2 (0.36) y SO2 (0.15), mientras que O3 presenta correlaciones inversas tanto con CO (-0.41) como con NO2 (-0.42). PM2.5 exhibe correlaciones débiles y negativas con ICAMAX, CO y NO2. Estos resultados destacan a CO como la variable más fuertemente correlacionada con ICAMAX, lo que proporciona una guía crítica para seleccionar las combinaciones de entrada descritas en la Tabla 2.
Resultados de los modelos de IA
Esta sección analiza los resultados de rendimiento de cada modelo, considerando las combinaciones de entrada descritas en la Tabla 3, el tipo de modelo de IA empleado y las métricas de evaluación asociadas.
Resultados CNN
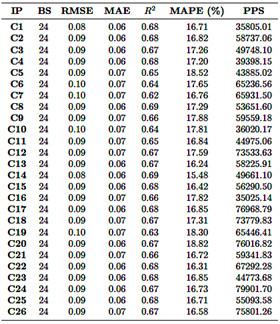
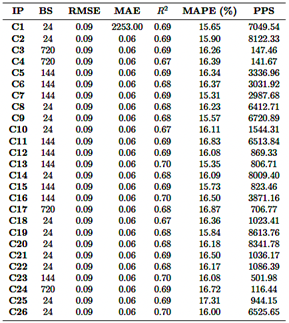
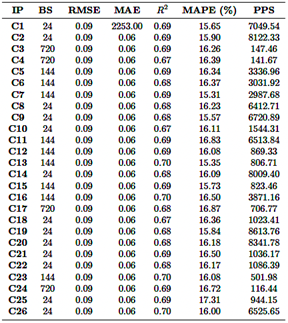
El modelo CNN fue evaluado utilizando 26 combinaciones diferentes de parámetros de entrada, todas basadas en una ventana deslizante de 24 horas (Tabla 4). El valor de R2 varió de 0.620 a 0.698, siendo la combinación de CO, O3, PM2.5 y SO2 (fila 24) la que alcanzó el mejor rendimiento con un valor de R2 de 0.698. Por otro lado, la combinación que involucraba NO2 y SO2 (fila 7) obtuvo el rendimiento más bajo, con un R2 de 0.620. En cuanto a las métricas de error, el RMSE osciló entre 0.087 y 0.097, mientras que el MAE varió de 0.060 a 0.068. Cabe destacar que la combinación de CO, O3, PM2.5 y SO2 también mostró los errores más bajos, lo que resalta aún más su rendimiento superior.
Los valores de MAPE, que indican la precisión de la predicción, variaron entre 15.48 % y 18.83 %. Las combinaciones que involucraban CO y O3 mostraron los valores más bajos de MAPE, lo que refleja una mayor precisión en la predicción. Por el contrario, las combinaciones que incluían NO2 y PM2.5 presentaron valores más altos de MAPE, lo que indica una menor precisión en la predicción. La eficiencia computacional varió significativamente, con tasas de predicción que oscilaron entre 35 805 y 79 091 predicciones por segundo. Las combinaciones más complejas, como CO, NO2, O3, PM2.5 y SO2 (fila 26), requirieron hasta 4.5 GB de RAM, pero lograron tasas de predicción superiores.
En resumen, la combinación de CO, O3, PM2.5 y SO2 (fila 24) resultó ser la más precisa, alcanzando el R2 más alto, los errores más bajos y una fuerte eficiencia computacional. En contraste, las combinaciones que incluían NO2 y SO2 tuvieron un rendimiento inferior en todas las métricas, lo que sugiere que estas variables tienen un impacto menor en la precisión de la predicción.
Donde:
IP: parámetros de entrada
BS: mejor ventana
PPS: predicciones por segundo
Resultados RNN
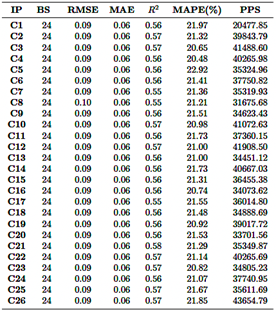
El modelo RNN fue evaluado utilizando 26 combinaciones diferentes de parámetros de entrada dentro de una ventana deslizante de 24 horas (Tabla 5). Los valores de R2 variaron de 0.533 a 0.576, siendo la combinación de CO, NO2, O3 y PM2.5 (fila 21) la que alcanzó el R2 más alto de 0.576. Por el contrario, la combinación que involucraba NO2 y SO2 (fila 7) mostró el rendimiento más bajo, con un R2 de 0.533. Los valores de RMSE variaron entre 0.092 y 0.097, mientras que el MAE osciló entre 0.058 y 0.063, siendo la combinación de CO, NO2, O3 y PM2.5 la que presentó los índices de error más bajos, lo que indica un rendimiento superior.
Los valores de MAPE variaron entre 20.48 % y 22.92 %, observándose los valores más bajos en las combinaciones que incluían CO y PM2.5, lo que sugiere una mejor precisión en la predicción. En contraste, las combinaciones que involucraban NO2 and O3 presentaron valores más altos de MAPE, lo que indica una menor precisión. La eficiencia computacional varió significativamente, con tasas de predicción que oscilaban entre 20 478 y 43 654 predicciones por segundo. Las combinaciones más complejas, como CO, NO2, O3, PM2.5 y SO2 (fila 26), requirieron hasta 23.4 GB de RAM, pero demostraron una mayor capacidad de predicción.
En conclusión, la combinación de CO, NO2, O3 y PM2.5 resultó ser la más precisa, alcanzando el R2 más alto, los menores índices de error y una fuerte eficiencia computacional. En contraste, las combinaciones que incluían NO2 y SO2 presentaron un rendimiento inferior de manera consistente en todas las métricas, lo que sugiere que estas variables tienen un impacto limitado en la precisión de la predicción.
Resultados LSTM
El modelo LSTM fue evaluado utilizando 26 combinaciones diferentes de parámetros de entrada, principalmente con una ventana deslizante de 24 horas, aunque algunas configuraciones emplearon ventanas de 144 horas o 720 horas (Tabla 6). Los valores de R2 variaron entre 0.669 y 0.701, siendo la combinación de CO, NO2, PM2.5 y SO2 (fila 23) la que alcanzó el R2 más alto de 0.701. Por el contrario, la combinación de NO2, O3 y SO2 (fila 18) mostró el R2 más bajo, con 0.669. Los valores de RMSE variaron entre 0.087 y 0.092, mientras que el MAE osciló entre 0.056 y 0.062, siendo la combinación de CO, NO2, PM2.5 y SO2 la que presentó los menores valores de error, lo que indica un rendimiento superior.
Los valores de MAPE variaron entre 15.31 % y 17.31 %, siendo los valores más bajos observados en las combinaciones que incluyen CO y NO2, lo que indica una mayor precisión en la predicción. Por el contrario, las combinaciones que involucraron NO2 y PM2.5 mostraron valores más altos de MAPE, lo que sugiere una menor precisión. La eficiencia computacional varió significativamente, con tasas de predicción que oscilaron entre 116 y 8613 predicciones por segundo. Las ventanas deslizantes más cortas generalmente resultaron en tasas de predicción más altas, pero requirieron un mayor uso de RAM. Por ejemplo, combinaciones complejas como CO, NO2, O3, PM2.5 y SO2 (fila 26) demandaron hasta 4.4 GB de RAM y lograron tasas de predicción moderadas. En contraste, combinaciones más simples como CO y NO2 requirieron menos RAM (3.3 GB) pero exhibieron tasas de predicción más bajas.
En resumen, la combinación de CO, NO2, PM2.5 y SO2 (fila 23) surgió como la más precisa, logrando el valor más alto de R2 y las mejores métricas de error, aunque con mayores demandas computacionales. Por el contrario, las combinaciones que involucraron NO2 and SO2 mostraron un rendimiento consistentemente inferior en todas las métricas evaluadas.
Resultados del modelo Transformer
En términos de métricas de error, el RMSE varió entre 0.094 y 0.130, y el MAE entre 0.068 y 0.099, con los errores más bajos observados para la combinación de CO, NO2, PM2.5 y SO2. Se observaron errores más altos, particularmente en el MAE, para combinaciones que involucraban CO y SO2, lo que sugiere que estos insumos son menos efectivos para predicciones precisas. Los valores de MAPE variaron entre 18.19 % y 26.83 %, con los valores más bajos asociados con combinaciones que involucraban O3 y PM2.5, mientras que se observaron valores más altos de MAPE para combinaciones que incluían NO2 y O3 (fila 2).
En cuanto a la eficiencia computacional, las predicciones por segundo variaron entre 2974 y 21 030. Las combinaciones más complejas, con un mayor número de parámetros de entrada y ventanas deslizantes más largas, requirieron un mayor uso de RAM (hasta 3.7 GB), pero lograron tasas de predicción más rápidas. Por el contrario, las combinaciones más simples, como CO y NO2, requirieron menos RAM (1.8 GB) pero presentaron tasas de predicción más lentas. En general, la combinación de CO, NO2, PM2.5 y SO2 (fila 23) resultó ser la más precisa, logrando el mayor R2 y las métricas de error más bajas, aunque con mayores requisitos computacionales. En contraste, las combinaciones que involucraban NO2 y O3 mostraron un rendimiento inferior en todas las métricas.
Análisis de los resultados del modelo de IA
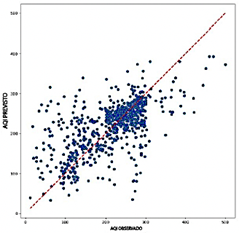
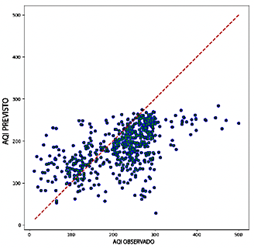
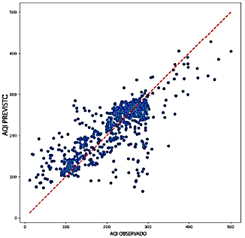
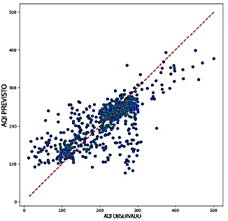
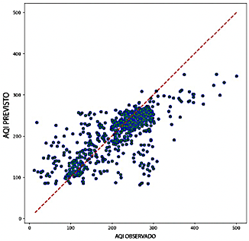
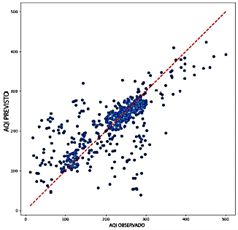
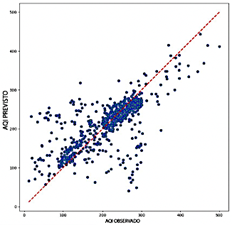
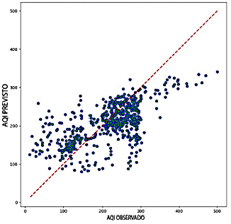
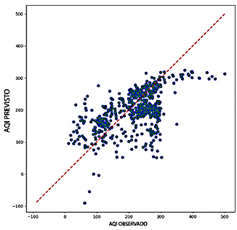
Al comparar el rendimiento de los modelos RNN, CNN, LSTM y Transformer, el Transformer presenta una precisión notablemente más baja, con valores de R2 que oscilan entre 0.322 y 0.640. Este amplio rango resalta los desafíos significativos para capturar la variabilidad de los datos de salida, particularmente al utilizar variables como NO2 y O3 Si bien Transformer demuestra una mayor eficiencia computacional requiriendo entre 1.8 GB y 3.7 GB de RAM y logrando tasas de predicción entre 2,974 y 21,030 predicciones por segundo esta eficiencia no compensa su menor precisión predictiva. Como se ilustra en la Figura 12, los diagramas de dispersión para el modelo Transformer muestran una dispersión considerable alrededor de la línea de referencia, particularmente en valores extremos de ICA. Esta desviación resalta la falta de fiabilidad del modelo en estas situaciones.
El modelo RNN, aunque más preciso que el Transformer, demuestra un rendimiento intermedio con valores de R2 que oscilan entre 0.533 y 0.576. El RNN alcanza una precisión aceptable, con valores de RMSE entre 0.092 y 0.097 y valores de MAE que varían entre 0.058 y 0.063. Sin embargo, sus valores de MAPE, que van de 20.48 % a 22.92 %, son más altos que los observados para los modelos CNN y LSTM. Como se muestra en la Figura 13, los diagramas de dispersión del RNN exhiben una mayor densidad de puntos cerca de la línea y = x en comparación con el modelo Transformer, lo que sugiere una mejor alineación general con los valores observados. No obstante, persiste una dispersión significativa en los niveles extremos de ICA, lo que resalta la variabilidad en la precisión al predecir valores altos o bajos de ICA.
En términos de eficiencia computacional, el RNN exhibe un rendimiento equilibrado, con un uso de RAM que varía entre 22.8 GB y 23.4 GB y tasas de predicción entre 20,478 y 43,654 predicciones por segundo. Aunque no es excepcional, este rendimiento posiciona al RNN como una opción viable, ofreciendo una compensación razonable entre precisión y eficiencia.
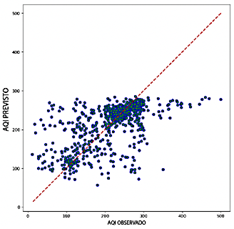
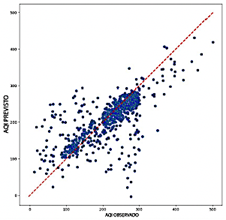
El modelo CNN exhibió un rango de R2 más alto, de 0.620 a 0.698, lo que demuestra su fuerte capacidad para capturar la variabilidad de los datos y proporcionar predicciones precisas. Entre las combinaciones probadas, CO, O3, PM2.5, and SO2 produjeron el mejor rendimiento. Los errores fueron relativamente bajos, con valores de RMSE entre 0.087 y 0.097 y valores de MAE que variaron entre 0.060 y 0.068. Además, los valores de MAPE entre 15.31 % y 18.83 % subrayaron aún más la precisión predictiva del modelo. Como se ilustra en la Figura 14, los diagramas de dispersión muestran la capacidad del modelo CNN para entregar predicciones consistentes, con una notable agrupación de puntos de datos alrededor de la línea de regresión, incluso en valores extremos, minimizando así los errores. Aunque el modelo CNN es menos eficiente computacionalmente que el Transformer, mantiene un equilibrio razonable, con un uso de RAM que varía entre 3.8 GB y 4.5 GB y una tasa de predicción de 35,805 a 79,091 predicciones por segundo.
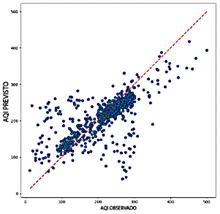
El modelo LSTM demuestra una precisión superior entre los modelos evaluados, con un rango de R2 de 0.669 a 0.701, destacando su excepcional capacidad para discernir patrones dentro de los datos. Supera a otros modelos en métricas de error, logrando valores de RMSE entre 0.087 y 0.092 y valores de MAE que varían entre 0.056 y 0.062. Además, el modelo LSTM exhibe los valores más bajos de MAPE, que van de 15.31 % a 17.31 %, subrayando su notable precisión predictiva. Como se ilustra en la Figura 15, los diagramas de dispersión para el modelo LSTM revelan una alta concentración de puntos de datos cerca de la línea de referencia, con una dispersión mínima, incluso para valores extremos de ICA. Esta consistencia y precisión posicionan al LSTM como una opción robusta y confiable para aplicaciones donde la precisión es crítica.
Sin embargo, el modelo LSTM es el menos eficiente computacionalmente entre los evaluados, con un uso de RAM que varía entre 3.3 GB y 4.5 GB y velocidades de predicción entre 116 y 8613 predicciones por segundo. Esta ineficiencia relativa, especialmente cuando se utilizan ventanas deslizantes más largas, puede limitar su aplicabilidad en escenarios donde la velocidad de procesamiento es crítica. No obstante, su precisión excepcional lo establece como una opción altamente confiable para aplicaciones donde la precisión prevalece sobre la eficiencia computacional.
Comparación con estudios realizados
Este estudio evalúa la efectividad de los modelos LSTM, GRU, RNN, CNN y Transformer para predecir el índice de calidad del aire en Cuenca, Ecuador, y compara los resultados con los hallazgos de otras investigaciones relevantes, como el estudio realizado por Cui et al. [36], que se centró en la predicción de PM2.5 utilizando modelos Transformer y CNN-LSTMAttention en Pekín, China.
Una distinción clave entre los estudios radica en los conjuntos de datos y sus características. Este estudio utiliza datos de una única estación meteorológica en Cuenca, que comprende 7425 registros del año 2022. En contraste, el estudio de Pekín emplea datos de 12 estaciones de monitoreo recolectados durante cuatro años (2013-2017), sumando más de 35 000 registros. El conjunto de datos más amplio en Pekín permitió a los investigadores incorporar variaciones estacionales y dependencias a largo plazo, factores críticos para una predicción precisa de PM2.5. Además, su modelo Transformer fue mejorado con mecanismos de atención de múltiples cabezas y codificación posicional, lo que permitió una captura más efectiva de patrones temporales complejos y fluctuaciones estacionales [36].
En cuanto al rendimiento del modelo, este estudio demostró que el modelo LSTM alcanza la mayor precisión para la predicción del ICA en Cuenca, con un R2 de 0.701, superando el rendimiento del modelo Transformer, que logró un R2 aproximado de 0.68. Por el contrario, en el estudio de Pekín, el modelo Transformer superó significativamente a la arquitectura CNN-LSTM-Attention, alcanzando un R2 de 0.944 frente a 0.836. Este rendimiento superior se atribuyó a la capacidad del Transformer para manejar tanto cambios meteorológicos abruptos como tendencias a largo plazo, particularmente durante transiciones estacionales complejas como las observadas en otoño e invierno [36].
Otra diferencia notable es el horizonte de predicción. Este estudio evaluó ventanas de predicción a corto y medio plazo (4, 24 y 120 horas), mientras que el estudio de Pekín se centró en predicciones horarias. El modelo Transformer en Pekín demostró ser particularmente efectivo para capturar variaciones repentinas de contaminantes impulsadas por cambios meteorológicos, lo que subraya su idoneidad para predicciones de alta frecuencia en entornos dinámicos [36].
Estos hallazgos subrayan la necesidad de adaptar las arquitecturas de IA a las características únicas de conjuntos de datos específicos y objetivos de predicción. Las investigaciones futuras deben centrarse en el desarrollo de modelos híbridos que aprovechen las fortalezas complementarias de las arquitecturas LSTM y Transformer, con el objetivo de abordar de manera efectiva los desafíos de pronóstico de la calidad del aire tanto a nivel local como regional.
Conclusiones
En este estudio, se evaluó y comparó el rendimiento de varios modelos de inteligencia artificial, incluyendo RNN, CNN, LSTM y Transformers, para la tarea de predecir el Índice de Calidad del Aire (ICA). Los hallazgos revelan que el modelo LSTM superó consistentemente a los otros modelos, logrando un R2 de 0.701 y un RMSE de 0.087. Su rendimiento superior fue particularmente evidente cuando se utilizaron combinaciones de variables como CO, NO2, PM2.5 y SO2. El análisis subraya la efectividad del modelo LSTM para capturar relaciones temporales complejas entre estas variables, estableciéndolo como una herramienta confiable y valiosa para la predicción precisa del ICA en diversos escenarios.
Aunque los modelos Transformers han demostrado un rendimiento excepcional en diversos campos como el procesamiento de lenguaje natural (NLP) y la visión por computadora (CV), su aplicación a la predicción del ICA, particularmente con este conjunto de datos específico, revela limitaciones significativas. En este estudio, los Transformers exhibieron una variabilidad notable en su rendimiento, con coeficientes de determinación que oscilan entre 0.322 y 0.640. Estos hallazgos sugieren que los Transformers enfrentan desafíos para capturar eficazmente la complejidad intrínseca de los datos de series temporales analizados, particularmente cuando se utilizan combinaciones de variables que incluyen NO2 and O3. A pesar de su eficiencia computacional, la precisión predictiva de los Transformers para el ICA no alcanza a la de modelos más competitivos como el LSTM.
En términos de eficiencia computacional, tanto los modelos CNN como LSTM han demostrado su idoneidad para aplicaciones en tiempo real, ofreciendo un equilibrio efectivo entre precisión y utilización de recursos. El modelo LSTM, en particular, se destaca por su excepcional precisión predictiva, un uso eficiente de la RAM de aproximadamente 4.4 GB y su capacidad para realizar un gran número de predicciones por segundo. Esta combinación de alto rendimiento y eficiencia en el uso de recursos hace que el LSTM sea especialmente adecuado para sistemas de predicción de la calidad del aire que requieren respuestas rápidas y precisas, como las aplicaciones de monitoreo ambiental en tiempo real.
A pesar de lograr valores satisfactorios de R2, el análisis reveló una considerable dispersión de los datos y métricas de error elevadas en todas las implementaciones, lo que hace que algunos modelos no sean adecuados para un despliegue confiable. Este estudio sirve como una evaluación comparativa de los enfoques de inteligencia artificial, destacando tanto las fortalezas como las limitaciones de las arquitecturas de IA actuales para la predicción del ICA. Los hallazgos subrayan la necesidad de refinamiento en las implementaciones existentes, al mismo tiempo que enfatizan el considerable potencial de los modelos de IA para mejorar las predicciones de la calidad del aire en el futuro.
En conclusión, el entrenamiento de todos los modelos encontró limitaciones debido al tamaño relativamente pequeño del conjunto de datos de Cuenca y a la baja correlación observada entre ciertos contaminantes. Para investigaciones futuras, recomendamos aprovechar conjuntos de datos más grandes y extender el análisis a lo largo de períodos más largos para mejorar el rendimiento de los modelos y generar conocimientos más sólidos.
Direcciones futuras
La selección de las arquitecturas de Long Short-Term Memory (LSTM), Convolutional Neural Networks (CNN), Transformer y Recurrent Neural Networks (RNN) como modelos fundamentales en este estudio se basó en su prominencia establecida en el análisis de series temporales y sus contribuciones significativas a los avances en la investigación de IA. Sobre la base de estas arquitecturas fundamentales, las investigaciones futuras deben explorar la incorporación de modelos mejorados basados en Transformer mediante la integración de mecanismos de atención multicabeza y esquemas de codificación posicional. Estos avances podrían permitir una modelización más sofisticada de las dependencias temporales en los patrones de calidad del aire.
La implementación de redes neuronales informadas por física (PINN) también presenta una dirección prometedora, ya que estas arquitecturas integran explícitamente las ecuaciones fundamentales de la física atmosférica y el transporte químico en el marco de redes neuronales. Este enfoque ofrece el potencial de cerrar la brecha entre las metodologías basadas en datos y los modelos teóricos, mejorando la interpretabilidad y la precisión de las predicciones.
Si bien las arquitecturas establecidas como Transformers, CNN, RNN y LSTM han demostrado una notable eficacia, explorar metodologías emergentes como ecuaciones diferenciales ordinarias neuronales (Neural ODE), Transformers de Fusión Temporal y redes Informer podría generar incluso mayores capacidades predictivas. Estos enfoques novedosos, aunque menos adoptados en la investigación de IA, podrían abordar los desafíos existentes en la modelización de dinámicas atmosféricas no lineales y complejas correlaciones intervariables, llevando la predicción del ICA a nuevos niveles de precisión y fiabilidad.