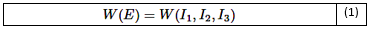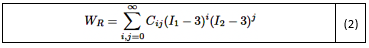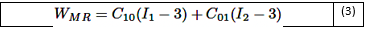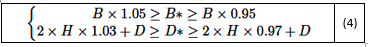Introducción
Los neumáticos son los únicos componentes de un vehículo que están en contacto directo con la carretera. Convierten el par en fuerza en la zona de contacto, permitiendo el movimiento del vehículo e influyendo significativamente en el rendimiento de conducción y maniobrabilidad [1, 2]. La zona de contacto del neumático, estrechamente asociada con la resistencia al rodamiento [3,4], impacta directamente en las pérdidas de energía, el consumo de combustible, las emisiones de gases de efecto invernadero y la durabilidad de la banda de rodadura. En consecuencia, el desempeño de contacto de los neumáticos ha sido ampliamente estudiado, con un enfoque particular en el tamaño y la forma de la zona de contacto entre el neumático y la carretera [5-9]. El método de elementos finitos (FE) y técnicas experimentales avanzadas se han empleado extensamente para analizar el desempeño de contacto de los neumáticos [10-13]. Guo et al. mejoraron el modelo de fuerza lateral UniTire [14], demostrando que la zona de contacto desempeña un papel crítico en la rigidez al giro y la longitud de relajación lateral. Patrick et al. [15] desarrollaron un modelo de cepillo 3D para caracterizar el tamaño y la distribución de presión de la zona de contacto. Alobaid et al. [16] mejoraron un modelo acoplado rígido-elástico en el plano al incorporar el movimiento vertical de la rueda como un cuerpo rígido. Este modelo conecta las irregularidades de la carretera como entrada a la zona de contacto y produce el movimiento vertical de la rueda como salida. Además, Fathi et al. [17] establecieron un modelo de elementos finitos de neumáticos utilizando la formulación arbitraria lagrangiana-euleriana para análisis en estado estacionario. Sin embargo, estos modelos a menudo requieren recursos computacionales sustanciales y numerosas suposiciones de parámetros, lo que presenta desafíos para su aplicación práctica.
Para validar los resultados de las simulaciones, se han desarrollado sistemas de películas de medición de presión [18-22] para capturar la distribución de presión en la interfaz neumático-carretera y analizar las relaciones entre las características geométricas de la huella y el desgaste de la banda de rodadura. Además, se han empleado técnicas de visión por computadora y sensores láser para neumáticos para medir con mayor precisión las zonas de contacto y la deformación del neumático [23, 24].
Tomaraee et al. [25] utilizaron un probador de rueda única bien equipado para examinar la relación entre el tamaño de la huella, la carga y la presión de inflado. Swami et al. [26] desarrollaron una aplicación de correlación de imágenes digitales estéreo (DIC) para generar visualizaciones tridimensionales (3D) de las zonas de contacto y extraer información dimensional.
Xie et al. [27] establecieron un modelo tridimensional de elementos finitos (FE) neumático-pavimento para estudiar la influencia de los neumáticos diagonales y radiales en la distribución de las tensiones de contacto. Sus resultados demostraron que la tensión de contacto máxima entre un neumático radial y la superficie de la carretera supera la de un neumático diagonal.
Wang et al. [28] analizaron el efecto del coeficiente de fricción en la tensión de contacto horizontal utilizando un modelo de simulación mejorado que incorpora un material de caucho neo-hookeano y una estructura de pavimento multicapa.
Oubahdou et al. [29] examinaron el contacto neumático-pavimento mediante una descripción realista de las secciones normales y las curvaturas, proporcionando análisis detallados de la forma de la zona de contacto, la distribución de tensiones y las tensiones cortantes superficiales en la interfaz neumáticopavimento.
Jaime et al. [30] investigaron la influencia de la rigidez del pavimento en las tensiones de contacto 3D utilizando un modelo de FE validado. Sus hallazgos indicaron que, aunque la rigidez del pavimento afecta mínimamente las tensiones normales de contacto, impacta significativamente las tensiones de contacto longitudinales. Utilizando un modelo no lineal de FE para neumáticos.
Liu et al. [31] desarrollaron una herramienta para la predicción rápida y precisa de tensiones de contacto no uniformes en la interfaz neumático-pavimento, integrando técnicas de aprendizaje profundo. Las relaciones entre la carga de la rueda y el comportamiento de la zona de contacto han sido ampliamente exploradas [32-34]. Zhang et al. [35] construyeron un modelo de contacto para neumáticos con patrón sobre pavimento asfáltico, analizando el comportamiento de contacto bajo carga estática y condiciones de ABS. Sus resultados revelaron que el área de contacto durante el frenado es un 7.7 % menor que bajo carga estática. Comparaciones de distribuciones de presión de contacto en condiciones estáticas y de rodadura utilizando modelos de FE para neumáticos han demostrado que el frenado, la aceleración y el giro impactan significativamente en las distribuciones de tensiones de contacto, con un aumento en la longitud de la zona de contacto a medida que disminuye la velocidad del neumático [36, 37].
Gu et al. [38] concluyeron que la longitud longitudinal de la zona de contacto disminuye con un mayor nivel de presión de inflado. La anchura de la zona de contacto debe considerarse para el análisis de tensiones laterales [39].
La zona de contacto desempeña un papel crucial en el rendimiento del neumático, influyendo en el desgaste de la banda de rodadura, la capacidad de respuesta de la dirección, el manejo en condiciones húmedas y secas, la tracción, el ruido del neumático y la calidad de conducción. Por lo tanto, investigar la zona de contacto del neumático es esencial para optimizar su desempeño. Entre los factores que afectan la zona de contacto, la relación de aspecto del neumático es un contribuyente significativo. Sin embargo, son limitados los estudios que han explorado la relación entre la relación de aspecto del neumático y la zona de contacto. Este estudio tiene como objetivo examinar los efectos de la relación de aspecto del neumático en la zona de contacto bajo diversas condiciones de carga vertical y presión de inflado. Se desarrollaron modelos de elementos finitos (FE) del neumático 205/55R16 utilizando ABAQUS 6.14, y se validaron comparando los resultados de simulación de carga y deformación con datos experimentales. También se establecieron modelos FE adicionales de neumáticos con relaciones de aspecto del 55 %, 60 %, 65 %, 70 % y 75 %. El estudio analizó las formas de las huellas y las distribuciones de tensiones de contacto bajo diferentes cargas verticales y presiones de inflado.
El artículo está estructurado de la siguiente manera: comienza con una descripción de los materiales del neumático y el proceso de modelado, seguido por la validación de los modelos de elementos finitos (FE). La sección de discusión explora posteriormente la relación entre la relación de aspecto del neumático y la zona de contacto en condiciones estáticas.
Materiales y métodos
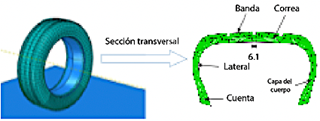
El modelo de elementos finitos (FE) y la sección transversal del neumático 205/55R16 se ilustran en la Figura 1. El ancho de la sección transversal del neumático es de 205 mm, con una relación de aspecto (altura/ancho) del 55 %. El diámetro de la llanta mide 406,4 mm, y el radio de la rueda es de 315,95 mm. Se desarrollaron modelos FE adicionales con relaciones de aspecto del 60 %, 65 %, 70 % y 75 %, ajustando el ancho de la sección transversal mientras se mantenía constante la altura del neumático.
El pavimento y la llanta se simplificaron como superficies rígidas debido a que su rigidez es significativamente mayor que la del neumático. Para garantizar una mayor calidad de la malla, solo se consideró el patrón de la banda de rodadura longitudinal en el modelo del neumático, omitiendo el patrón transversal. Las secciones transversales bidimensionales del neumático se crearon utilizando el software AutoCAD y posteriormente se importaron a ABAQUS para desarrollar los modelos tridimensionales. Se incorporaron dos cinturones en la simulación: el cinturón 1, ubicado más cerca de la banda de rodadura, con un ancho de 94 mm, y el cinturón 2, con un ancho de 114 mm. Se aplicó una fuerza concentrada a lo largo del eje Z en el punto central de la llanta. Se utilizó un método de discretización para la interacción neumático-pavimento con el fin de predecir el contacto superficie a superficie. Se empleó una función de penalización para simular el comportamiento de contacto tangencial, con un coeficiente de fricción establecido en 0,8. Además, se refinó la malla de contacto para mejorar la precisión de las predicciones del modelo.
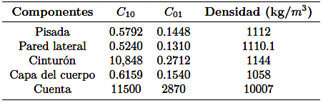
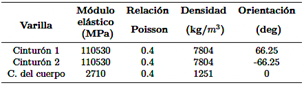
Las propiedades mecánicas hiperelásticas de los materiales de caucho se describen utilizando el modelo constitutivo de Mooney-Rivlin [40]. Las propiedades del material correspondientes se presentan en la Tabla 1. En este estudio, la deformación del caucho se modela como una deformación uniforme de cuerpos isotrópicos hiperelásticos. En consecuencia, la densidad de energía de deformación se expresa utilizando invariantes de deformación de la siguiente manera:
Donde I3 = 1 dado que el material es completamente incompresible, la ecuación (1) se simplifica a:
Donde, Cij , representan los coeficientes del material. Para aplicaciones prácticas en ingeniería, la ecuación (2) se reduce aún más a:
El compuesto caucho-cuerda se simuló utilizando elementos de varilla para tener en cuenta tanto los materiales de caucho como los de cuerda simultáneamente, con cada material mallado por separado. Las propiedades del material de varilla se enumeran en la Tabla 2. Se aplicó presión de inflado a la superficie interna del neumático para simular diversas condiciones de inflado. De acuerdo con la norma GB/T 2977-2016, los parámetros del neumático se definen como:
Donde, B es el ancho de sección diseñado del neumático, B* es el ancho de sección del neumático inflado, HH es la altura de la sección, DD es el diámetro de la llanta, y D* es el diámetro del neumático inflado.
Validación del modelo
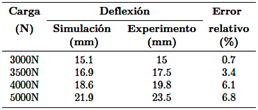
Para validar el modelo, se comparó la relación entre la deformación del neumático y la carga estática con datos experimentales de la referencia [41]. Los experimentos se realizaron utilizando una máquina de prueba de rigidez de neumáticos 5-en-1 (keD · TEK, Taiwan Hung Ta Instrument Co. Ltd.) con un desplazamiento máximo de 1500 mm y una precisión de ± 0.1 mm. El neumático probado fue un 205/55 R16, con una presión de neumático de 0.24 MPa. Se aplicaron cargas radiales de 3000 N, 3500 N, 4000 N y 5000 N. Se utilizaron los mismos parámetros en las simulaciones de elementos finitos (FE). El error más grande entre los resultados de simulación y experimentales fue del 6.8 %, lo que indica que el modelo simplificado de neumático FE es razonable y adecuado para investigar la relación entre la relación de aspecto y la zona de contacto neumático-suelo. Los resultados de simulación y experimentales para la deformación bajo diferentes cargas estáticas se presentan en la Tabla 3.
Resultados y discusión
El tamaño y la forma de la zona de contacto bajo diferentes cargas verticales
La Figura 2 ilustra las zonas de contacto de los neumáticos con diferentes relaciones de aspecto bajo cargas verticales de 3000 N, 4000 N y 5000 N.
La presión de inflado se estableció en 0.24 MPa. La Figura 2 muestra que la zona de contacto presentó una forma de silla de montar para las relaciones de aspecto del 55 % y 60 %, se transformó en una forma rectangular para una relación de aspecto del 65 %, y evolucionó a una forma de tambor de cintura para relaciones de aspecto del 70 % y 75 %. Para caracterizar mejor la zona de contacto, se midieron la longitud y el ancho de la banda de rodadura en contacto. La longitud de contacto de la banda de rodadura se refiere a la longitud máxima de la zona de contacto a lo largo de la dirección de rodadura del neumático, mientras que el ancho de contacto de la banda de rodadura representa el ancho máximo de la zona de contacto a lo largo de la dirección axial del neumático.
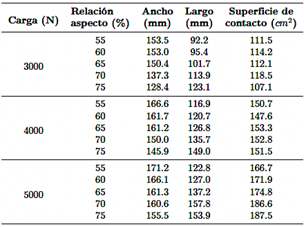
Las áreas de contacto para diferentes relaciones de aspecto, obtenidas de las simulaciones de ABAQUS, se presentan en la Tabla 4. Los resultados indican que, a medida que aumenta la relación de aspecto, el ancho de contacto de la banda de rodadura disminuye, mientras que la longitud de contacto de la banda de rodadura aumenta bajo la misma carga estática. Además, para una relación de aspecto dada, tanto el ancho como la longitud de contacto de la banda de rodadura, así como el área total de la zona de contacto, aumentan con cargas verticales más altas.
Tabla 4 El tamaño de la zona de contacto de los neumáticos con diferentes relaciones de aspecto bajo diferentes cargas verticales
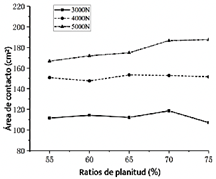
La Figura 3 ilustra las relaciones entre la relación de aspecto y el área de la zona de contacto bajo diferentes cargas verticales. Los resultados indican que el área de la zona de contacto aumenta a medida que aumenta la carga vertical. Bajo cargas de 3000 N y 4000 N, el área de la zona de contacto fluctúa con el aumento de la relación de aspecto, mientras que bajo una carga de 5000 N, aumenta de manera constante con relaciones de aspecto más altas. La relación entre la relación de aspecto del neumático y el área de la zona de contacto es no lineal. Un área de zona de contacto más grande generalmente da como resultado una reducción de las vibraciones y el ruido, así como en un mejor rendimiento de agarre. Sin embargo, un área mayor de zona de contacto también conduce a un mayor desgaste promedio de la banda de rodadura y a una mayor pérdida de energía. Bajo las tres cargas verticales, el neumático, con una relación de aspecto del 55 %, presentó un área de contacto relativamente más pequeña.
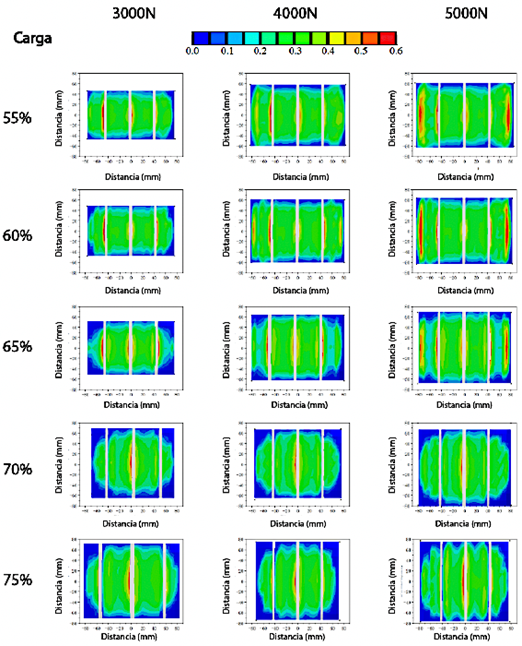
Figura 2 La forma de las zonas de contacto de los neumáticos con diferentes relaciones de aspecto bajo diferentes cargas verticales.
Distribución de las tensiones de contacto bajo diferentes cargas verticales
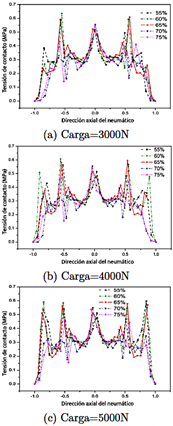
La Figura 4 presenta la distribución de tensiones de contacto de los neumáticos a lo largo del camino de nodos para diferentes relaciones de aspecto bajo diversas cargas verticales.
Las curvas de tensión de contacto a lo largo del ancho de la banda de rodadura exhiben un patrón de múltiples picos, con los valores máximos principalmente concentrados en el hombro y la ranura longitudinal. Esto se debe a la concentración de tensiones causadas por cambios dramáticos en la forma de la banda de rodadura en el hombro y la ranura. Para la carga vertical de 3000 N, como se muestra en la Figura 4a, el valor máximo de la tensión de contacto se distribuyó principalmente en la ranura de la banda de rodadura, y los valores máximos de los neumáticos con una relación de aspecto del 60 % y 65 % fueron mayores que los de neumáticos con otras relaciones de aspecto. Para la carga vertical de 4000 N, como se muestra en la Figura 4b, la tensión de contacto aumentó notablemente en el hombro. La máxima tensión de contacto ocurrió en el hombro del neumático con una relación de aspecto del 60 %.
Para una carga vertical de 5000 N, como se muestra en la Figura 4c, la tensión de contacto en ambos lados de la banda de rodadura disminuyó con un aumento en la relación de aspecto, mientras que la tensión de contacto en el centro de la banda de rodadura aumentó. La máxima tensión de contacto se observó en el hombro del neumático para relaciones de aspecto del 55 %, 60 % y 65 %. En contraste, para relaciones de aspecto del 70 % y 75 %, la máxima tensión se desplazó hacia la parte central de la banda de rodadura. Las regiones con mayores tensiones de contacto típicamente experimentan un desgaste más severo [42]. Además, dado que el centro de la banda de rodadura es más delgado, las relaciones de aspecto del 70 % y 75 % pueden reducir la vida útil del neumático.
Tamaño y forma de la zona de contacto bajo diferentes presiones de inflado
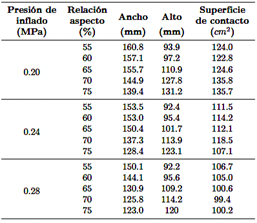
Los tamaños de las zonas de contacto de los neumáticos bajo diferentes presiones de inflado se presentan en la Tabla 5. El ancho de la zona de contacto disminuyó progresivamente a medida que aumentaba la relación de aspecto, mientras que la longitud de la zona de contacto aumentó bajo la misma presión de inflado. Tanto el ancho como la longitud de la zona de contacto, así como su área total, disminuyeron con el aumento de la presión de inflado para una relación de aspecto dada. La Figura 5 ilustra las zonas de contacto de los neumáticos con diferentes relaciones de aspecto bajo presiones de inflado de 0.20, 0.24 y 0.28 MPa. La carga vertical se estableció en 3000 N. Los resultados muestran que la forma de la zona de contacto pasó de una forma de silla de montar a una forma de tambor de cintura a medida que aumentaba la relación de aspecto bajo la misma presión de inflado. Además, a medida que aumentaba la presión de inflado, la distribución de la tensión de contacto se volvía más desigual.
Tabla 5 Tamaño de la zona de contacto de los neumáticos con diferentes relaciones de aspecto bajo diversas presiones de inflado
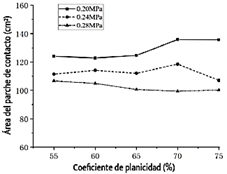
La Figura 6 ilustra la relación entre la relación de aspecto y el área de la zona de contacto bajo diversas presiones de inflado. Los datos revelan que el área de la zona de contacto disminuye a medida que aumenta la presión de inflado. Con una presión de inflado de 0.2 MPa, el área de la zona de contacto aumenta a medida que la relación de aspecto sube del 60 % al 70 %. Para una presión de inflado de 0.24 MPa, el área de la zona de contacto fluctúa con el aumento de la relación de aspecto. Por el contrario, con una presión de inflado de 0.28 MPa, el área de la zona de contacto disminuye a medida que la relación de aspecto aumenta. En las tres condiciones de presión de inflado, los neumáticos con una relación de aspecto del 55 % mostraron consistentemente áreas de zona de contacto relativamente más pequeñas.
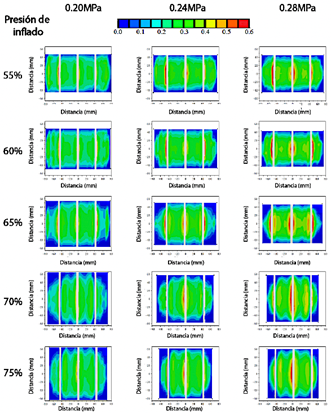
Figura 5 Formas de la zona de contacto de los neumáticos con diferentes relaciones de aspecto bajo diferentes presiones de inflado
Distribución de la tensión de contacto bajo diferentes presiones de inflado
La presión de contacto es un factor crítico en el rendimiento de un vehículo, ya que influye directamente en la adherencia y tracción. Estos parámetros están estrechamente asociados con las capacidades de aceleración, frenado y toma de curvas del vehículo. Aunque una mayor presión de contacto generalmente mejora la adherencia, una presión excesiva puede acelerar el desgaste prematuro del neumático.
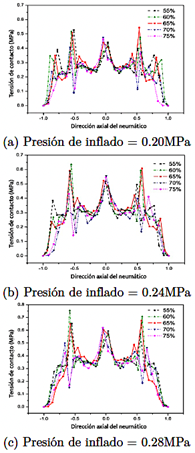
La Figura 7 ilustra la distribución de la tensión de contacto de los neumáticos a lo largo de la ruta de los nodos para diferentes relaciones de aspecto bajo diversas presiones de inflado. Las curvas de tensión de contacto a lo largo del ancho de la banda de rodadura exhibieron un patrón de múltiples picos. A medida que aumentaba la presión de inflado, la tensión de contacto en los hombros disminuía, mientras que la tensión en las ranuras longitudinales aumentaba. Cuando la presión de inflado se estableció en 0.20 MPa (Figura 7a), el valor máximo de la tensión de contacto permaneció por debajo de 0.6 MPa. En contraste, con presiones de inflado de 0.24 MPa y 0.28 MPa (Figuras 7b y 7c), la tensión de contacto máxima superó los 0.6 MPa. En todas las presiones de inflado, la tensión de contacto máxima en las ranuras a ambos lados de la banda de rodadura para neumáticos con relaciones de aspecto del 60 % y 65 % fue mayor que la de otros neumáticos con distintas relaciones de aspecto. Por el contrario, la tensión de contacto en la ranura central de la banda de rodadura para las relaciones de aspecto del 60 % y 65 % fue menor que la observada en otras relaciones de aspecto bajo condiciones de inflado idénticas.
Una distribución desigual de la presión de contacto conduce a un desgaste irregular de los neumáticos. Como se muestra en la Figura 7a, los neumáticos con relaciones de aspecto del 70 % y 75 % presentan una tensión de contacto más baja y más uniforme en comparación con aquellos con relaciones de aspecto del 55 %, 60 % y 65%.
Esto sugiere una mayor probabilidad de desgaste irregular para los neumáticos con relaciones de aspecto más bajas. Cuando la presión de inflado aumentó de 0.2 MPa a 0.24 MPa (Figura 7b), esta disparidad se hizo más pronunciada. Además, la tensión de contacto en el hombro de los neumáticos con relaciones de aspecto más bajas es mayor que en los neumáticos con relaciones de aspecto más altas, lo que indica una mejor estabilidad y manejo durante las curvas. La tensión de contacto en el centro de la banda de rodadura es casi idéntica en todas las relaciones de aspecto, siendo las principales diferencias observadas en el hombro y las ranuras longitudinales.
Conclusiones
Este estudio presenta modelos de elementos finitos (FE) de neumáticos 205/XX R16 desarrollados utilizando el software ABAQUS para investigar el tamaño y la forma de la huella de contacto, así como la distribución axial de la presión de contacto dentro de la huella de contacto de neumáticos con diferentes relaciones de aspecto bajo diferentes cargas estáticas de rueda y presiones de inflado. Las principales conclusiones son las siguientes:
1. Los resultados de la simulación FE para la deflexión del neumático bajo diferentes cargas estáticas se alinean estrechamente con los datos experimentales, con un error máximo del 6.8 %, lo que confirma la precisión y fiabilidad del modelo.
2. El ancho de la banda de rodadura de la huella de contacto disminuyó y la longitud aumentó a medida que aumentaba la relación de aspecto. El área de la huella de contacto fluctuó con el aumento de la relación de aspecto bajo cargas estáticas de 3000 N y 4000 N, mientras que aumentó de manera consistente bajo una carga estática de 5000 N. La forma de la huella de contacto evolucionó de una forma de silla de montar a una forma de tambor de cintura a medida que aumentaba la relación de aspecto.
3. Las presiones de inflado más bajas dieron como resultado en áreas de huella de contacto más grandes y una distribución más uniforme de la tensión de contacto. A medida que aumentaba la presión de inflado bajo la misma carga estática de rueda, la tensión de contacto en el centro de la banda de rodadura aumentaba.
4. La distribución de la tensión de contacto a lo un patrón multipico, con los picos ubicados principalmente en el hombro y las ranuras longitudinales. Para los neumáticos con relaciones de aspecto del 55 %, 60 % y 65 %, la máxima tensión de contacto se observó en el hombro. En contraste, para los neumáticos con relaciones de aspecto del 70 % y 75 %, la máxima tensión se produjo en el centro de la banda de rodadura.