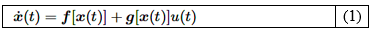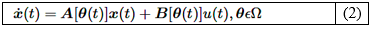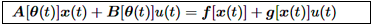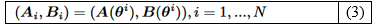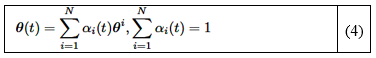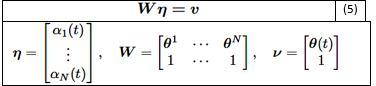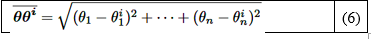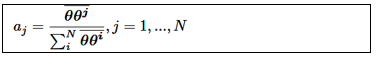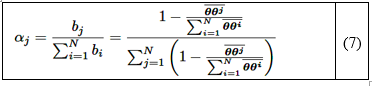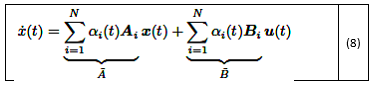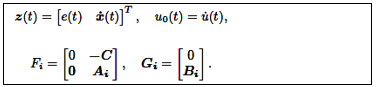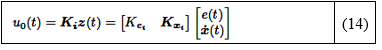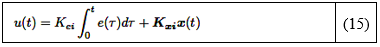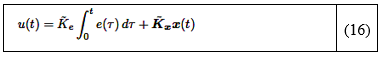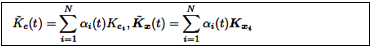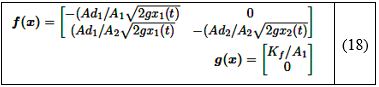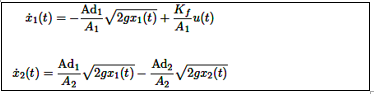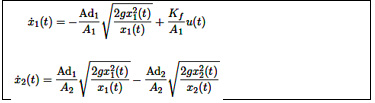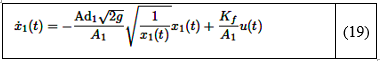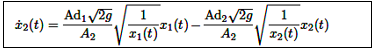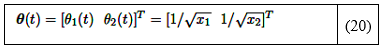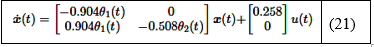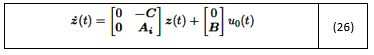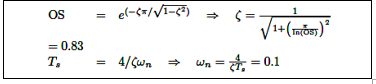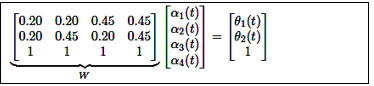Introducción
El control de niveles de líquido en tanques se emplea ampliamente en diversas industrias, incluyendo la producción de alimentos y bebidas, plantas nucleares y petroquímicas, y el sector farmacéutico. Generalmente, las interacciones entre tanques ocurren debido al acoplamiento, dando como resultado un comportamiento no lineal [1]. Se han propuesto numerosas estrategias de control para sistemas de tanques acoplados, incluyendo controladores proporcionales-integrales-derivativos (PID) [2-4], control difuso [5, 6], control predictivo basado en modelos [7, 8], control backstepping [9,10], control por modo deslizante [11,12], controladores PID fraccionarios [13, 14], control robusto [15], control de rechazo activo de perturbaciones [16, 17] y controladores de dos grados de libertad [18]. Algunas de estas técnicas se basan en la teoría de sistemas no lineales, lo cual puede ser complejo de implementar, mientras que otras emplean la linealización de las ecuaciones del sistema alrededor de un punto de operación. Para el rango operativo local, los diseños basados en la linealización jacobiana son efectivos. Sin embargo, ante perturbaciones significativas o cuando se requieren tiempos de asentamiento más rápidos, el desempeño de tales controladores puede deteriorarse debido a una pérdida de robustez.
La programación de ganancia [19,20] es un enfoque ampliamente adoptado en la industria para controlar sistemas no lineales al descomponer el problema de diseño no lineal en varios subproblemas manejables donde se pueden aplicar herramientas de diseño lineal. Por ejemplo, en el control de robots, la dinámica del controlador se ajusta en tiempo real en función de la variación de la inercia y la geometría. De manera similar, la mayoría de las leyes de control de aeronaves se modifican interpolando controladores diseñados individualmente.
En las últimas décadas, la teoría de sistemas lineales de parámetros variables (LPV) ha ganado prominencia como un paradigma poderoso para la identificación de sistemas, el análisis y la síntesis de controladores [21-23]. Esta clase de sistemas es particularmente valiosa, ya que permite incorporar no linealidades como parámetros variables dentro de un conjunto acotado, asegurando que las trayectorias posibles del sistema LPV abarquen todas las trayectorias del sistema no lineal original.
Cuando estos parámetros incluyen elementos del vector de estado, el sistema se denomina cuasi-LPV [24]. En este estudio, las no linealidades del modelo del sistema de tanques, representadas por los niveles de líquido, se consideran inciertas, pero están restringidas dentro de los límites tecnológicos del equipo ([0, 30] cm). Esto permite una representación precisa de los términos no lineales al integrarlos en un modelo cuasi-LPV. La ventaja de este enfoque es que permite el diseño de controladores lineales al usar técnicas de espacio de estados, asegurando un error de seguimiento en estado estacionario nulo para entradas de referencia constantes y garantizando un criterio de dominancia de polos [25, 26].
Dentro de un esquema de programación de ganancia, el control del sistema de tanques acoplados no lineal se logra mediante la interpolación de controladores locales. Se proponen dos mecanismos de interpolación: (1) interpolación analítica, donde se resuelve continuamente un sistema de ecuaciones lineales para calcular los factores de ponderación, y (2) interpolación geométrica, donde los pesos de los controladores locales se determinan en función de la distancia euclidiana a ciertos puntos vértice.
La interpolación analítica, presentada inicialmente en [27] e inspirada en conceptos de los modelos difusos de Takagi-Sugeno, se implementa en este estudio de forma simplificada sin incorporar elementos difusos. La interpolación geométrica, por otro lado, ofrece un enfoque innovador en este contexto. Si bien la teoría cuasi-LPV ha sido ampliamente aplicada en campos como la guía de misiles [28,29] y la robótica [30,31], su aplicación en sistemas de tanques sigue siendo relativamente inexplorada a pesar de la significativa relevancia industrial de este proceso.
Los resultados confirman la efectividad del método propuesto para el control del sistema de tanques acoplados. El artículo se estructura de la siguiente manera: la Sección 2 detalla el método de diseño de control cuasi-LPV, con un enfoque particular en la formulación de dos mecanismos de interpolación, los cuales se integran dentro de una estrategia de control de seguimiento con programación de ganancia, ademas describe el modelo no lineal del sistema de tanques acoplados. En la Sección 3, el método de diseño cuasi-LPV se aplica al sistema. Finalmente, en la Sección 4 se presentan las conclusiones.
Notación: Las letras mayúsculas en negrita representan matrices, mientras que las letras minúsculas en negrita representan vectores (es decir, θ 𝑗 es el componente j-th del vector θ). Los superíndices indican vectores; por ejemplo, θi se refiere al vector i-th, y 𝜃 𝑗 𝑖 denota el componente j-th del vector i-th. 𝑓 (𝑡)= 𝑑𝑓(??) 𝑑𝑡 y 𝑓 𝑡 = 𝑑 2 𝑓(𝑡) 𝑑𝑡 2 . ℝ denota el conjunto de los números reales.
Materiales y métodos
Diseño de control cuasi-LPV
La mayoría de los enfoques existentes para la síntesis de controladores no lineales se centran en sistemas afines a la entrada [32], que suelen describirse como en la ecuación (1):
Donde: ℝ + → ℝ 𝑛 es el vector de estado, 𝑢: ℝ + →ℝ es la entrada de control, t es la variable independiente del tiempo, f: ℝ 𝑛 → ℝ 𝑛 y 𝒈: ℝ 𝑛 → ℝ 𝑛 n son campos no lineales. La ecuación no lineal general 𝒙 𝑡 =𝒇 𝒙 𝑡 , 𝑢(𝑡) , que aparece frecuentemente, puede, bajo supuestos técnicos, transformarse en (1) mediante una transformación de retroalimentación no lineal [33].
El primer paso en el procedimiento de síntesis es derivar una representación cuasi-LPV de la forma, como se ve en la ecuación (2):
Para el sistema no lineal descrito en la ecuación (1). Aquí, θ representa un vector de parámetros que varía dentro de una caja de límites Ω. En el modelado cuasi-LPV, se asume que existe una relación entre el vector de parámetros y los estados del sistema, 𝜽=𝝈 𝒙 , tal que para todos los valores de parámetros dentro de Ω.
Mecanismos de interpolación
Definiendo 𝜽 𝑖 ∈ ℝ 𝑛 , 𝑖=1,…, 𝑁 en (2) como los vectores que representan las combinaciones extremas de parámetros en Ω, se obtiene un conjunto de modelos linealizados locales como se muestra en la ecuación (3):
Para cada modelo local, se puede diseñar una ganancia del vector de estado 𝑲 𝑖 . Luego, el vector de parámetros 𝜽 𝑡 se utiliza para construir el controlador global con programación de ganancia mediante la interpolación de los controladores locales. En cualquier momento dado, 𝜽 ?? puede expresarse como se muestra en la ecuación (4):
Los pesos α_i (t) se calculan resolviendo el sistema de ecuaciones lineales como se muestra en la ecuación (5):
Donde:
El esquema de interpolación basado en los pesos calculados a partir de la solución continua de la ecuación (5) se denomina interpolación analítica para distinguirla de la interpolación geométrica, que se describirá a continuación.
En cualquier momento dado, la distancia euclidiana entre el vector de parámetros dependiente del estado vector 𝜽∈ ℝ 𝑛 y cualquiera de los vectores extremos 𝜽 𝒊 ∈ ℝ 𝑛 dentro de la caja de límites Ω se puede calcular para 𝑖=1,…,𝑁 como se muestra en la ecuación (6):
La contribución relativa del vector de parámetros θ(t) en cada vértice θ i se da por:
Los puntos más alejados de los vértices deben tener pesos más bajos. Por lo tanto, se utiliza la distancia complementaria, 1− 𝜽 𝜽 𝒊 , en el cálculo. La contribución relativa complementaria se calcula entonces como 𝑏 𝑗 =1− 𝑎 𝑗 , 𝑗=1,…,𝑁. Finalmente, el peso 𝛼 𝑗 𝑡 para 𝑗=1,…, 𝑁 en cualquier momento dado se determina como se muestra en la ecuación (7):
Como en el procedimiento analítico, los pesos calculados utilizan el enfoque geométrico satisfacen continuamente la ecuación 𝑗=1 𝑁 𝛼 𝑗 (𝑡) =1. La diferencia clave entre los dos métodos es que el enfoque geométrico asegura pesos positivos, mientras que el procedimiento analítico no lo garantiza. Esto puede requerir el acondicionamiento de la entrada de control si el actuador solo opera con señales positivas.
Seguimiento de una entrada de referencia escalonada
Usando los pesos calculados, el modelo en la ecuación (2) se puede aproximar como una combinación de los modelos lineales locales como se muestra en la ecuación (8):
El problema de diseño ahora se centra en el seguimiento de una entrada de referencia escalonada r(t) con error en estado estacionario cero e(t) definido como se muestra en la ecuación (9):
Donde la ecuación (10) es la salida controlada. Tomando la derivada temporal de la ecuación (9), para una entrada de referencia constante se obtiene la ecuación (11):
Tomando la derivada temporal de cada modelo lineal local 𝑨 𝑖 , 𝑩 𝑖 para 𝑖=1,…,𝑁 se obtiene la ecuación (12):
Las ecuaciones (11) y (12) se pueden combinar como se muestra en la ecuación (13):
Donde:
Una ganancia de retroalimentación de estado para el sistema, ver la ecuación (13), se construye como se muestra en la ecuación (14):
Después de integrar la ecuación (14), la señal de control real se convierte en lo que se muestra en la ecuación (15):
Usando los mismos pesos 𝛼 𝑖 𝑡 , se construye una ganancia de retroalimentación de estado dependiente del tiempo para el sistema descrito en la ecuación (8) y como se muestra en la ecuación (16):
Donde:
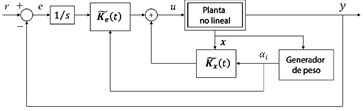
La Figura 1 ilustra la implementación de la política de control descrita en la ecuación (15) para cada modelo local, como se define en la ecuación (3). Además, la Figura 2 muestra el controlador global que permite la implementación de la ley de control en la ecuación (16) mediante la interpolación de los controladores locales, utilizando ya sea pesos calculados analíticamente (ecuación 5) o geométricamente (ecuación (7)). Para el sistema de seguimiento aumentado en la ecuación (13), la ganancia 𝑲 𝑖 = 𝐾 𝑒 𝑖 1×1 𝑲 𝒙 𝑖 1×𝑛 se calcula para cada 𝑖=1,…,𝑁 resolviendo un problema de colocación de polos en lazo cerrado usando el comando de MATLAB, ver ecuación (17):
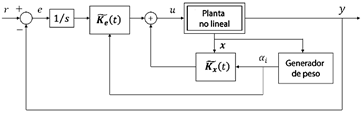
Figura 2 Implementación del controlador de seguimiento general mediante la interpolación de controladores locales
Donde P representa los polos deseados en el lazo cerrado, seleccionados para satisfacer un criterio garantizado de dominancia de polos [25], [26], basado en los requisitos de diseño en lazo cerrado especificados en el dominio del tiempo, como el sobrepaso (OS) y el tiempo de establecimiento (Ts). A la luz de la discusión anterior, el algoritmo de diseño para implementar la ley de control interpolada en la ecuación (16) se resume en la Tabla 1.
Sistema de tanques acoplados
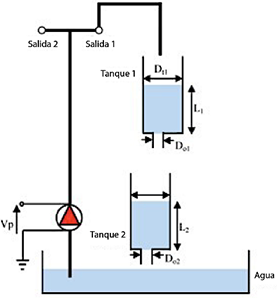
La Figura 3 muestra el sistema de tanques acoplados. Consiste en una bomba única y dos tanques, cada uno equipado con un sensor de presión para medir el nivel de agua. La bomba transfiere agua del reservorio inferior al superior del sistema. Dependiendo de la configuración de las válvulas de salida, el agua puede fluir hacia el tanque superior, el tanque inferior o ambos. Esta configuración se ilustra en la Figura 4, donde la salida de la bomba está conectada al primer tanque.
x1 y x2 representan los niveles de agua en los tanques 1 y 2, respectivamente. Las funciones vectoriales en la forma de la ecuación (18) para el sistema de tanques acoplados se derivan utilizando la ley de Bernoulli y el principio de balance de masa [34] y se expresan como se detalla en la ecuación (18):
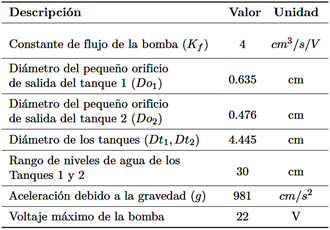
Donde A1 y A2 denotan las áreas de sección transversal de los tanques 1 y 2, respectivamente. Ad1,Ad2 representan las áreas de sección transversal de los orificios correspondientes, g es la aceleración debido a la gravedad en la Tierra, y Kf es la constante de flujo de la bomba. Los valores numéricos de estos parámetros se proporcionan en la Tabla 2.
Resultados y discusión
Esta sección describe la implementación y evalúa el rendimiento del método de control cuasi-LPV, como se resume en la Tabla 1.
Modelo cuasi-LPV
El voltaje de entrada aplicado a la bomba sirve como la señal de control, mientras que el nivel de agua en el segundo tanque se selecciona como la salida controlada. Basado en la ecuación (18), el modelo no lineal del sistema de tanques se puede expresar como:
Los términos no lineales en cada ecuación pueden reformularse de la siguiente manera:
Lo que resulta en la ecuación (19):
Definiendo el vector de parámetros en (19) como:
Utilizando los valores numéricos de la Tabla 2, el modelo cuasi-LPV en la forma de la ecuación (2) se expresa como se muestra en la ecuación (21):
Los niveles de líquido en los tanques se consideran inciertos, pero varían dentro de sus límites físicos, como se especifica en la Tabla 2, a lo largo del intervalo:
Cuando los niveles de líquido en los tanques varían dentro del rango especificado en la ecuación (22), el vector de parámetros en la ecuación (20) fluctuará dentro de la caja rectangular:
Modelos linealizados locales
Las combinaciones extremas de parámetros dentro de la caja rectangular en la ecuación (23) dan lugar a los siguientes vectores:
Esto da lugar al siguiente conjunto de modelos linealizados locales: 𝑨 𝑖 , 𝑩 𝑖 = 𝑨 𝜽 𝑖 , 𝑩 para 𝑖=1,…, 4.
Controladores locales
Utilizando la ecuación (25), los sistemas aumentados en la ecuación (13) para cada vértice se dan por:
Las cuatro ganancias del controlador Ki en la ecuación (15) se calculan utilizando las especificaciones de lazo cerrado en el dominio del tiempo OS = 1% y Ts = 40s. El cálculo se realiza luego como se describe en [35].
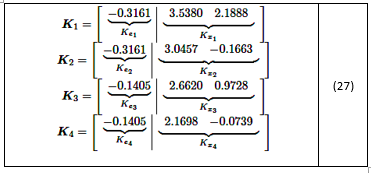
Los polos dominantes resultantes son p1,2 =−0.0996 ± j0.0669(s2 + 0.1992s + 0.0144). Los polos deseados para el lazo cerrado utilizados en la ecuación (17) son P = [−0.0996 ± j0.0669,−0.996], donde p3 = −0.996 es un polo rápido con influencia insignificante sobre las especificaciones de OS y Ts. Las ganancias del controlador se calculan utilizando la ecuación (17) de la siguiente manera:
Mecanismos de interpolación
En el enfoque analítico, la ecuación (5) se representa como el siguiente sistema de ecuaciones lineales:
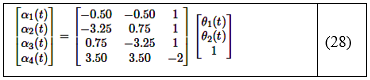
Resolver este sistema utilizando la matriz pseudoinversa (W T W) −1 WT da como resultado la ecuación (28):
Para la interpolación geométrica, la ecuación (7) se implementa directamente utilizando un bloque de función en MATLAB. Se escribe un código sencillo en MATLAB que se integra en un modelo de Simulink, el cual ejecuta la simulación.
Implementación del control programado por ganancias
Se implementó la estrategia de control programado por ganancias mostrada en la Figura 2. La Figura 5 ilustra la respuesta del nivel de líquido en el segundo tanque tras un cambio en el punto de referencia, comparando ambos métodos de interpolación para los controladores lineales calculados (27). El método geométrico presenta problemas específicos al inicio de la simulación debido a su incapacidad para proporcionar la acción de control negativa requerida. Después de esta fase inicial, el desempeño de ambos esquemas de interpolación se vuelve comparable.
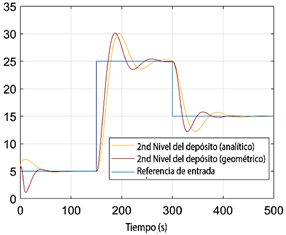
Figura 5 Respuesta del nivel de líquido en el segundo tanque en lazo cerrado para los métodos de interpolación analítica y geométrica
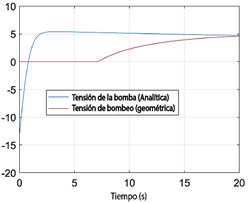
La Figura 6 ilustra la señal de control, mientras que la Figura 7 se enfoca en los primeros 20 segundos de la señal de control. Es evidente que cuando se requiere una señal de control negativa, el esquema geométrico permanece en cero, confirmando los problemas observados al inicio de la simulación, como se muestra en la Figura 5. Es importante señalar que la señal de control proporcionada por la bomba no puede ser negativa, una limitación no tenida en cuenta durante la simulación al evaluar el desempeño de ambos esquemas de interpolación. Un voltaje negativo se interpretaría como succión. Inicialmente, la señal de referencia cambia instantáneamente de cero, lo que provoca que la señal de control reaccione en sentido opuesto hasta que la referencia se estabiliza en un valor constante. A partir de ese momento, el controlador funciona adecuadamente con cualquiera de los esquemas de interpolación, aunque se requiere un mayor esfuerzo de control durante los períodos de cambio de la señal de referencia.
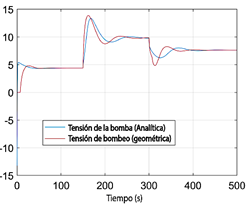
Figura 6 Señal de control de voltaje de la bomba para los métodos de interpolación analítica y geométrica
Resultados adicionales
La Figura 8 ilustra el cuadro de parámetros delimitado por la ecuación (23). Los resultados anteriores involucraron la implementación del controlador programado por ganancias mediante la interpolación, tanto geométrica como analítica, de los controladores locales calculados en los vértices (A), (B), (C) y (D), basados en un criterio de polos dominantes para las especificaciones deseadas de OS y Ts. Además, la simulación permitió que la señal de control tomara valores negativos para facilitar la comparación entre los dos mecanismos de interpolación.
El controlador programado por ganancias se implementa en esta sección, utilizando varios controladores locales calculados dentro de la región mostrada en la Figura 8, según lo especificado en la Tabla 3.
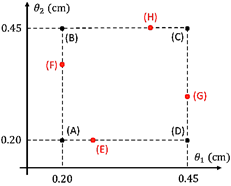
Figura 8 Puntos elegidos en el cuadro de parámetros delimitado por la ecuación (23) para calcular los controladores locales
La señal de control está restringida a permanecer dentro del rango operativo de la bomba (0 − 22V ), y los polos cerrados deseados en la ecuación (17) se seleccionan como P = [−0.1,−0.2,−10], en lugar de emplear el criterio de polos dominantes.
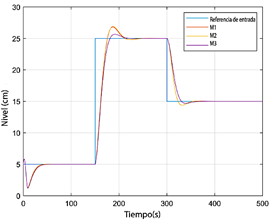
El modelo M1 utiliza los vértices de la región, el modelo M2 calcula los controladores locales a lo largo de los bordes, y el modelo M3 considera los vértices extremos de la región, donde los parámetros θ1 y θ2 toman sus valores mínimos y máximos posibles. La selección del modelo M3 está justificada por el conocido teorema del borde [36]. La Figura 9 ilustra el nivel en el segundo tanque y la señal de control de la bomba utilizando el modelo M1 con interpolación analítica.
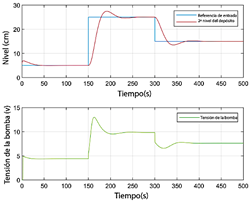
Figura 9 Nivel del segundo tanque y voltaje de la bomba para el modelo M1 con interpolación analítica
La Figura 10 presenta un escenario similar utilizando interpolación geométrica. Las Figuras 11 y 12 replican el análisis para el modelo M2, utilizando mecanismos de interpolación analítica y geométrica, respectivamente.
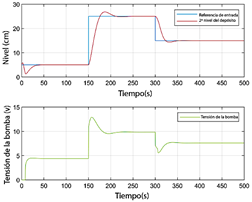
Figura 10 Nivel del segundo tanque y voltaje de la bomba para el modelo M1 con interpolación geométrica
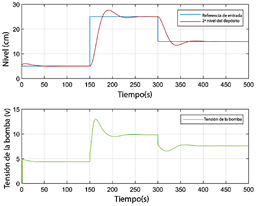
Figura 11 Nivel del segundo tanque y voltaje de la bomba para el modelo M2 con interpolación analítica
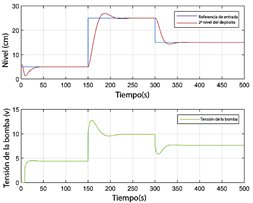
Figura 12 Nivel del segundo tanque y voltaje de la bomba para el modelo M2 con interpolación geométrica
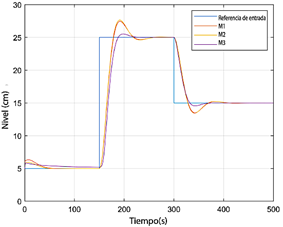
Las Figuras 13 y 14 muestran los resultados para el modelo M3, nuevamente utilizando interpolación analítica y geométrica. Finalmente, las Figuras 15 y 16 comparan la evolución del nivel de líquido en el segundo tanque para los tres modelos, considerando la interpolación analítica y geométrica.
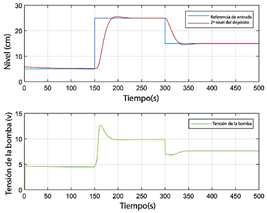
Figura 13 Nivel del segundo tanque y voltaje de la bomba para el modelo M3 con interpolación analítica
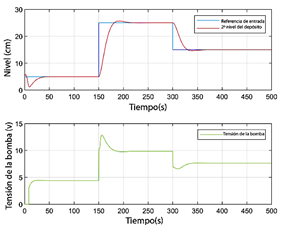
Figura 14 Nivel del segundo tanque y voltaje de la bomba para el modelo M3 con interpolación geométrica
Conclusiones
Se propuso un procedimiento con programación de ganancias para controlar un sistema de tanques acoplados modelado como un sistema cuasi-LPV. Las no linealidades del modelo se capturan directamente mediante un conjunto de parámetros inciertos que varían dentro de un conjunto acotado, restringido por los límites físicos del sistema de tanques. Se calcularon combinaciones extremas del vector de parámetros y se obtuvieron aproximaciones lineales locales. Estas aproximaciones se utilizaron luego en la síntesis de leyes de control en el espacio de estados para seguir una entrada de referencia constante. El controlador global se construyó como un promedio ponderado de las contribuciones locales, donde los pesos dependían de los valores instantáneos del vector de parámetros.
Se emplearon dos mecanismos de interpolación, geométrico y analítico, para determinar el promedio ponderado de los controladores lineales. El método geométrico se basa en la distancia euclidiana entre el vector de parámetros y los vértices, mientras que el método analítico consiste en resolver un sistema lineal de ecuaciones utilizando la pseudoinversa de una matriz. El esquema geométrico es más sencillo y genera solo acciones de control positivas, con un tiempo de cálculo muy corto. En contraste, el esquema analítico puede proporcionar tanto acciones de control positivas como negativas, pero requiere un tiempo de procesamiento significativamente mayor. Los resultados de la simulación demostraron que utilizar los dos vértices extremos (Modelo M3) para calcular los controladores locales interpolados reduce el esfuerzo computacional necesario.
La principal limitación de la metodología es el desafío de determinar con precisión el modelo cuasi-LPV para capturar las no linealidades del sistema, lo cual no es una tarea fácil para todas las plantas. Esto indica que el enfoque propuesto puede no ser aplicable de manera universal. Sin embargo, cuando una planta no lineal puede ser modelada efectivamente utilizando un sistema de parámetros variables lineales, el método es sencillo de implementar y ofrece resultados satisfactorios. Otro aspecto clave del método es que la ley de control para diseñar los controladores locales no está limitada a la asignación de polos en lazo cerrado, como se demostró en este artículo. Se pueden emplear diversas estrategias de control con realimentación de estado, incluidas aquellas que consideran la optimización, robustez y restricciones. Además, aunque el criterio de dominio de polos garantizado es adecuado para sistemas lineales, surgió una discrepancia notable entre las especificaciones de diseño y el rendimiento real en el caso del sistema de tanques no lineales. Esta brecha se mitigó estableciendo polos reales dominantes para mejorar el control sobre la salida.
El trabajo en curso se centra en la implementación en tiempo real del método de diseño propuesto y la inclusión de observadores de estado.