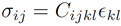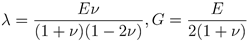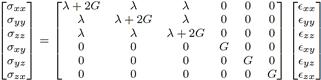1. Introducción
En las últimas dos décadas, ha habido un notable aumento en la adopción del método de elementos finitos (MEF) para el análisis de estructuras complejas [1]. Esta técnica numérica proporciona una solución aproximada altamente precisa para problemas que carecen de soluciones en forma cerrada.
En el análisis estático estructural mediante el método de elementos finitos (FEA), las leyes constitutivas describen cómo los materiales responden a cargas aplicadas y definen la relación entre el esfuerzo y la deformación. La ley de Hooke, presentada en la ecuación (1), es la ley constitutiva fundamental empleada para materiales elásticos lineales. Esta ley proporciona una relación lineal entre los tensores de esfuerzo (σij) y deformación (ϵkl), representada de la siguiente manera:
Cijkl es el tensor de rigidez elástica, que depende de propiedades del material como el módulo de Young (E) y el coeficiente de Poisson (ν).
En un escenario práctico de análisis por elementos finitos (FEA), varias variables son conocidas, incluyendo propiedades del material (módulo de Young, coeficiente de Poisson y densidad), geometría (dimensiones y forma de la estructura), y condiciones de contorno (desplazamientos como soportes fijos o movimientos prescritos, y fuerzas como cargas aplicadas o presión).
En el análisis por elementos finitos (FEA), las cantidades desconocidas incluyen los desplazamientos nodales (ui) en cada nodo de la malla, así como las deformaciones (ϵij) y los esfuerzos (σij) en cada punto de integración o nodo. Para un material elástico lineal en 3D, la matriz de rigidez puede expresarse utilizando las constantes de Lamé, λ y G, derivadas del módulo de Young y el coeficiente de Poisson.
La ecuación (3) presenta la relación esfuerzodeformación en forma matricial.
Al introducir las propiedades conocidas del material y las condiciones de contorno en el software de FEA, se pueden determinar las incógnitas (desplazamientos, deformaciones y esfuerzos). Este proceso garantiza una predicción precisa del comportamiento estructural bajo cargas aplicadas, facilitando el diseño y la evaluación de la integridad estructural.
Una revisión de la investigación publicada revela el uso prevalente de condiciones de contorno fijas en el análisis estructural estático de miembros aislados de la estructura global [2]. Aunque comúnmente empleado, se reconoce que esta condición de contorno representa una aproximación conservadora, que sobreestima el máximo esfuerzo en el miembro estructural, lo que conduce consecuentemente a una subestimación del factor de seguridad (FOS) [3].
El uso de condiciones de contorno de soporte fijo en el análisis de estructuras estáticamente indeterminadas, como las alas de aeronaves, presenta limitaciones significativas debido principalmente a las suposiciones que introducen los soportes fijos, las cuales pueden no reflejar con precisión las condiciones del mundo real [4]. Los soportes fijos asumen que no hay movimiento ni rotación en los puntos de soporte, lo cual frecuentemente es irrealista en escenarios prácticos. Las alas de aeronaves experimentan diversas fuerzas y momentos que causan deformaciones, lo que influye significativamente en el comportamiento estructural global [5]. Además, las uniones y conexiones en una aeronave no son perfectamente rígidas; poseen cierto grado de flexibilidad que debe considerarse para un análisis estructural más preciso.
Los soportes fijos pueden distorsionar los verdaderos caminos de carga y las distribuciones de esfuerzos dentro de la estructura. Las alas de las aeronaves están diseñadas para distribuir las cargas de manera eficiente, pero los soportes fijos pueden alterar estas distribuciones, lo que conduce a análisis inexactos [6]. Esto puede resultar en concentraciones artificiales de esfuerzos que no existen en la estructura, lo que potencialmente lleva a evaluaciones erróneas de la integridad estructural y la vida útil a fatiga.
Además, los soportes fijos simplifican las condiciones de contorno hasta un grado que puede no capturar con precisión las no linealidades del material, como la deformación plástica y el flujo viscoso [7]. A menudo, las alas de las aeronaves operan bajo condiciones donde estas no linealidades del material son significativas, lo que requiere condiciones de contorno que puedan tener en cuenta tales efectos. Además, las grandes deformaciones y las no linealidades geométricas en las alas de las aeronaves requieren condiciones de contorno que puedan adaptarse a configuraciones cambiantes, una capacidad que los soportes fijos no pueden proporcionar.
Por último, los resultados de los análisis utilizando soportes fijos pueden no correlacionarse bien con los datos experimentales o las mediciones en vuelo. Para garantizar un análisis preciso y confiable, los ingenieros a menudo recurren a condiciones de contorno más realistas que simulan la interacción entre las diferentes partes de la estructura y a soportes flexibles que incorporan la elasticidad de los accesorios y conexiones.
También se emplean modelos híbridos, que combinan diversas condiciones de contorno, para capturar mejor las complejas interacciones dentro de la estructura. Estas condiciones de contorno avanzadas facilitan predicciones más precisas del comportamiento estructural bajo diversas condiciones de carga, lo que conduce a diseños de aeronaves más seguros y eficientes.
El ala de una aeronave se clasifica como una estructura estáticamente indeterminada [8]. Estas estructuras presentan redundancia cinemática, donde las restricciones superan el mínimo necesario para evitar el movimiento rígido del cuerpo bajo cargas aplicadas. En estructuras estáticamente indeterminadas, los valores de las fuerzas y momentos de reacción en los soportes son influenciados por las características de rigidez de la estructura [9]. En consecuencia, la rigidez del ala juega un papel crucial en determinar la distribución de carga en los puntos de conexión de la estación del ala [10].
En lugar de imponer una condición de contorno fija en un modelo local aislado del modelo global, un enfoque alternativo implica asignar desplazamientos nodales derivados de la solución del modelo global de elementos finitos (FE) [11]. Se realiza un análisis de FE del miembro estructural aislado, incorporando estos desplazamientos nodales y la carga aplicada, para obtener resultados precisos. Este método requiere soluciones para ambos modelos, global y local, para cada caso de carga [12].
Una tercera técnica implica aislar el modelo local del modelo global utilizando resortes translacionales y rotacionales. La rigidez de estos resortes depende del campo de deformación del modelo global bajo la carga aplicada [13]. Posteriormente, se analiza un modelo local refinado utilizando estos resortes para cada caso de carga. La implementación de estos resortes en ANSYS se logra aplicando condiciones de contorno de soporte elástico, con rigidez derivada del análisis del modelo global del ala bajo la carga de diseño [14].
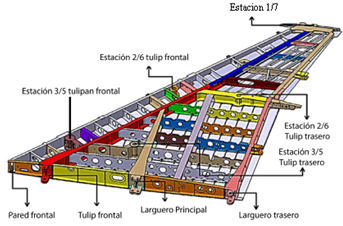
Este examen se centra en un avión de combate a reacción contemporáneo. La Figura 1 muestra el ala de una aeronave, que incluye cuatro largueros: el de la pared frontal, el frontal, el principal y el trasero [15]. Estos largueros constituyen un marco cohesivo interconectado intrincadamente a través de un sistema de doce costillas.
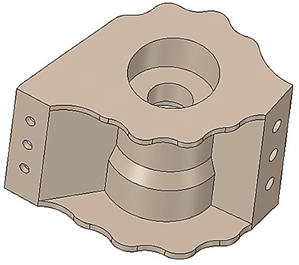
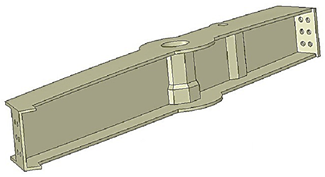
Este estudio se centra en la estación del ala externa 2/6, ubicada en la costilla del ala 7, específicamente designada para transportar cargas externas. Esta estación consta de dos componentes estructurales integrales: el tulip frontal (FT) y el tulip trasero (RT).
Considerando las limitaciones de las condiciones de contorno fijas, este estudio mejora la fidelidad del análisis incorporando la rigidez del ala. El objetivo principal es determinar la capacidad máxima de carga de la estación del ala 2/6, utilizando condiciones de contorno precisas a través de la técnica de submodelado [16].
Este método tiene como objetivo proporcionar una representación más precisa del comportamiento estructural, permitiendo una evaluación precisa de los niveles de esfuerzo y el Factor de Seguridad (FOS) para la estación del ala. La incorporación de la rigidez del ala mejora la fiabilidad del análisis estructural y proporciona percepciones detalladas sobre el rendimiento del ala bajo diversas condiciones. Las técnicas de submodelado tienen en cuenta la influencia de la rigidez del ala, lo que resulta en una mayor precisión y comprensión del comportamiento estructural. En última instancia, la integración de la rigidez del ala mejora la fiabilidad del análisis estructural, ofreciendo valiosas percepciones sobre el rendimiento del ala en varios escenarios.
2. Materiales y métodos
La metodología implica extraer el tulip frontal y trasero del modelo global del ala e introducir la rigidez del ala mediante condiciones de contorno elásticas derivadas del análisis de elementos finitos bajo la carga de diseño [17]. Se aplican cargas críticas a cada tulip del ala, y se realiza un análisis estructural estático en ANSYS Workbench versión 14.5 para generar el campo de deformación y esfuerzos. Utilizando el Factor de Seguridad (FOS) basado en la resistencia a la fluencia, el estudio determina la capacidad máxima de carga de la estación del ala. Se llevan a cabo análisis modales pre-estresados y de pandeo [18] para evaluar el efecto de rigidez por esfuerzos bajo la carga máxima de diseño. El verdadero potencial de este estudio reside en la optimización del diseño, que se implementa mediante alteraciones paramétricas de los agujeros de perno del tulip del ala. Este proceso mejora la capacidad de carga de la estación del ala, facilitando una evaluación integral del rendimiento estructural y mejorando las capacidades generales de la aeronave de combate [19]. Aunque este estudio proporciona una comprensión completa del comportamiento de la estación del ala bajo cargas estáticas, no tiene en cuenta condiciones de carga cíclica. El análisis PSD para carga cíclica se abordará en estudios posteriores.
3. Resultados y discusión
3.1. Condiciones de contorno para los tulip
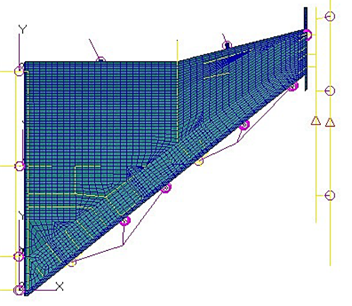
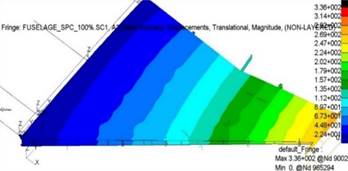
El modelo de elementos finitos (FE) del ala, construido utilizando elementos de línea y de cáscara, se ilustra en la Figura 2. El análisis de este modelo de ala bajo carga de diseño genera un campo de desplazamiento representado en la Figura 3. El campo de desplazamiento resultante bajo las cargas aplicadas proporciona valores de rigidez para los soportes elásticos impuestos como condición de contorno para el análisis de los tulip frontal y trasero.
Los valores de rigidez para los respectivos soportes elásticos, obtenidos a través de ANSYS Workbench versión 14.5, se presentan a continuación. Estos valores de rigidez se utilizan en el análisis de los tulip del ala aislados.
Las cargas aplicadas al ala se transfieren al fuselaje, causando deformación y movimiento en el centro de gravedad de la aeronave. Para eliminar el movimiento rígido del cuerpo en el análisis, es necesario restringir la línea central de la aeronave. En el estudio actual, el modelo de ala de la aeronave se restringe a seis grados de libertad (6 DOF) en la línea central de la aeronave.
Esta restricción evita movimientos rígidos no deseados, asegurando una transferencia precisa de carga y simulación del comportamiento estructural. Al aplicar estas restricciones, el análisis proporciona condiciones de contorno estables y realistas para el análisis por elementos finitos (FEA).
3.2. Modelos de elementos finitos de los tulip
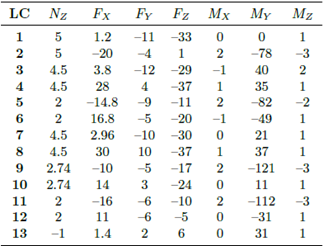
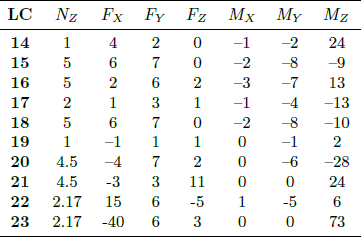
Los modelos CAD de los tulip frontal y trasero para la estación del ala 2/6, desarrollados en el módulo de diseño ANSYS Design Module®, se ilustran en la Figura 4 y Figura 5, respectivamente. Estos modelos CAD sirven como plantillas para desarrollar modelos de elementos finitos en ANSYS Workbench®. Las propiedades del material asignadas a los tulip del ala se detallan en el análisis aerodinámico de la aeronave con cargas externas dentro del envolvente de transporte de la aeronave, proporcionando casos críticos de carga para los tulip del ala [1]. La Tabla 3 y Tabla 4 describen exhaustivamente los casos de carga aplicados al Tulip Frontal (FT) y al Tulip Trasero (RT) durante el envolvente de transporte [1]. Estas fuerzas y momentos flectores se aplican tanto al tulip frontal como al trasero de la estación 2/6.
3.3. Análisis del tulip frontal (FT)
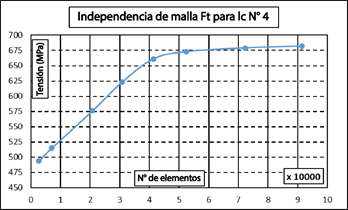
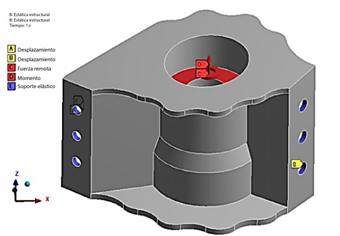
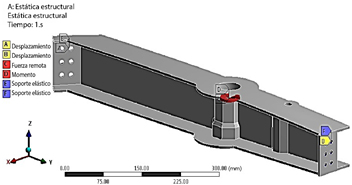
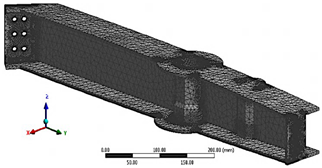
El modelo ha sido mallado libremente utilizando elementos Tet6, que son elementos tetraédricos con tres nodos y una función de forma cuadrática. Para asegurar la precisión, la malla se refina en los puntos críticos de tensión ubicados en los agujeros de perno. Como se ilustra en la Figura 6, un estudio de independencia de la malla establece que la solución se vuelve independiente del refinamiento de la malla a partir de 70 000 elementos. La Figura 7 muestra el modelo mallado del tulip frontal (FT), mientras que la Figura 8 ilustra las condiciones de contorno y cargas aplicadas en el FT.
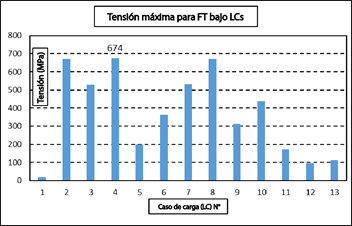
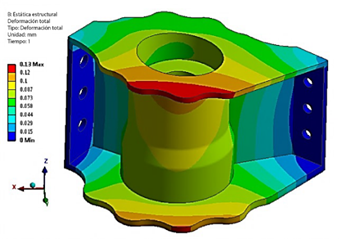
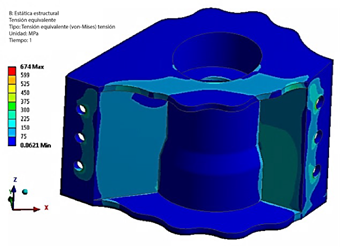
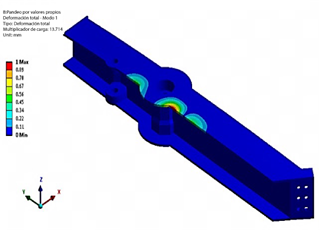
Para cada caso de carga, se generan gráficos de deformación y esfuerzo en ANSYS. La comparación del esfuerzo máximo equivalente (von Mises) para cada caso de carga en el tulip frontal (FT) se ilustra en la Figura 9. El caso de carga 4 se identifica como el caso crítico para el FT, con un valor de esfuerzo de 674 MPa. El campo de deformación del tulip frontal bajo el caso de carga crítico 4 se muestra en la Figura 10. Se observa una deformación máxima de 0,13 mm en el nervio del FT.
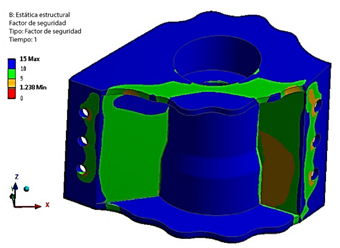
Se proporciona un mayor entendimiento de la respuesta estructural, específicamente el campo de esfuerzos resultante y el factor de seguridad (FOS), en la Figura 11 y Figura 12, respectivamente. El FOS del Tulip Frontal (FT) es de 1,23 bajo el caso de carga crítico 4, lo que indica que el FT se encuentra seguro dentro del envolvente de transporte. Estos análisis contribuyen a una comprensión integral del comportamiento estructural, evaluando márgenes de seguridad e identificando áreas potenciales para la optimización del diseño.
3.4. Análisis del tulip trasero (RT)
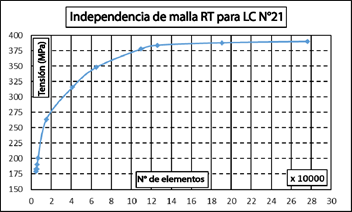
Se ha realizado el mallado libre del modelo del tulip trasero utilizando elementos Tet6, que son elementos tetraédricos con tres nodos y una función de forma cuadrática. Se implementa un refinamiento de malla en los agujeros de perno para capturar el gran gradiente de tensión en estos puntos críticos. Un estudio de independencia de la malla, como se ilustra en la Figura 13, demostró que la solución se volvió independiente del refinamiento de la malla a partir de 130 000 elementos.
La Figura 14 muestra el modelo mallado del tulip trasero (RT). La Figura 15 ilustra las condiciones de contorno y las cargas aplicadas, representadas como fuerzas y momentos.
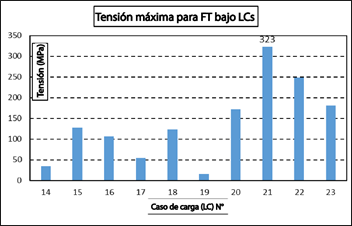
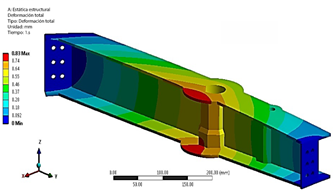
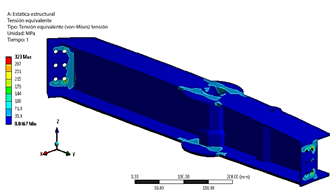
A través del análisis de elementos finitos (FE), se determinaron la deformación y el esfuerzo para cada caso de carga. La comparación del esfuerzo máximo equivalente (von Mises) para cada caso de carga en el tulip trasero (RT) se presenta en la Figura 16. El caso de carga crítico para el RT se identifica como el caso de carga 21, con un valor de esfuerzo de 323 MPa. La Figura 17 ilustra el campo de deformación del tulip trasero bajo el caso de carga 21. Se observa una deformación máxima de 0,83 mm bajo este LC crítico.
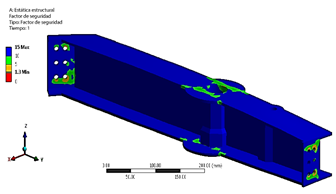
Se proporcionan información adicional sobre el campo de esfuerzos resultante y el factor de seguridad (FOS), bajo este caso de carga específico en la Figura 18 y Figura 19. El FOS del RT es de 1,3 bajo el crítico LC 21, lo que indica que el RT está seguro dentro del envolvente de transporte. Estos análisis exhaustivos contribuyen a una comprensión detallada del comportamiento estructural, ayudando en la evaluación de márgenes de seguridad y áreas potenciales para la optimización del diseño del tulip trasero.
3.5. Análisis modal y de modo preactivado
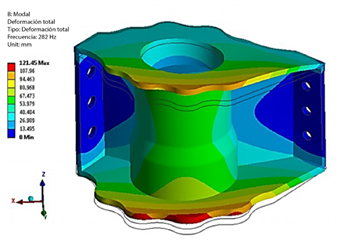
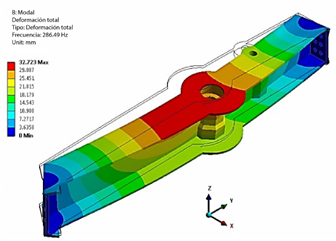
Se ha realizado un análisis modal de los tulip frontal y trasero de la estación del ala para explorar las características dinámicas de las vibraciones libres sin fuerzas externas [20]. Este análisis utilizó modelos de malla libre de los tulip frontal y trasero dentro del módulo modal de ANSYS. Las formas modales fundamentales para los tulip frontal y trasero se muestran en la Figura 20 y Figura 21, respectivamente. Las frecuencias modales fundamentales para el tulip frontal (FT) y el tulip trasero (RT) son 286 Hz y 282 Hz, respectivamente.
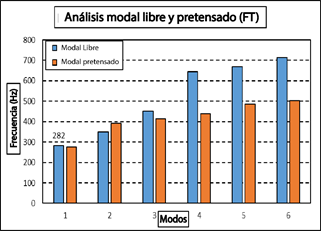
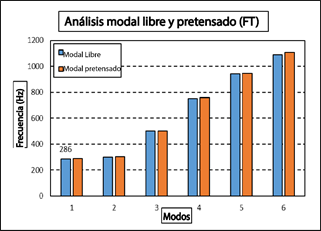
Además, se ha realizado un análisis modal preactivado ara evaluar los efectos de endurecimiento por esfuerzo. Se presenta una comparación entre las frecuencias modales libres y preactivadas para los tulip frontal y trasero en la Figura 22 y Figura 23, respectivamente. El análisis modal preactivado revela una disminución mínima en las frecuencias modales para el tulip frontal (FT). Para el tulip trasero (RT), no hay disminución en la frecuencia modal bajo el esfuerzo aplicado. Por lo tanto, el efecto de endurecimiento por esfuerzo para los tulip FT y RT es insignificante.
Un análisis comparativo ofrece información sobre cómo las condiciones preactivadas afectan el comportamiento modal de los tulip, proporcionando detalles sobre la respuesta estructural bajo la influencia de tensiones preexistentes. Estos hallazgos mejoran la comprensión integral de las características dinámicas de los tulip frontal y trasero.
3.6. Análisis de pandeo
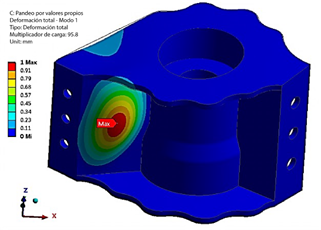
Se han realizado análisis de pandeo de los tulip frontal y trasero para determinar las cargas de pandeo y las correspondientes formas modales de pandeo [21]. Los resultados de estos análisis se muestran en la Figura 24 y Figura 25, que muestran el primer modo de pandeo para los tulip frontal y trasero, respectivamente, bajo sus casos de carga críticos.
Los multiplicadores de carga de pandeo para los tulip frontal y trasero se determinaron como 95 y 13, respectivamente, bajo casos de carga críticos. Estos altos multiplicadores de carga sugieren que el pandeo no es un modo de fallo probable para los tulip del ala. Las formas modales ofrecen información crucial sobre la estabilidad estructural de los tulip bajo condiciones de carga específicas, mejorando la identificación de posibles modos de fallo y la determinación de márgenes de seguridad para los componentes de la estación del ala.
3.7. Optimización
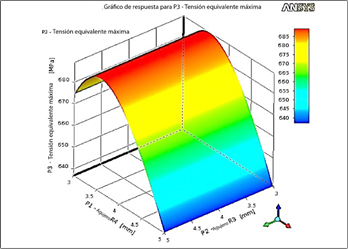
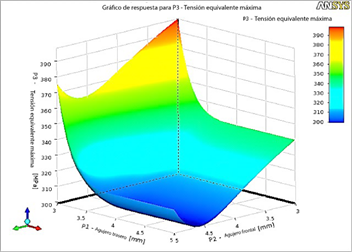
Los radios actuales para todos los agujeros de perno de los tulip son de 4 mm. Este estudio revela que el máximo esfuerzo bajo un caso de carga crítico ocurre en los agujeros de perno. Para realizar un análisis de sensibilidad al esfuerzo, el diámetro de los agujeros de perno varía de 6 a 10 mm utilizando el módulo de optimización de ANSYS [22]. La Figura 26 y la Figura 27 muestran las superficies de respuesta de esfuerzo en función de los radios de los agujeros de perno para el tulip frontal y el tulip trasero, respectivamente. Estas superficies muestran visualmente cómo los cambios en los radios de los agujeros de perno influencian el máximo esfuerzo de los tulip.
La Figura 26 indica que los radios de los pernos en el lado interior (P2) no tienen un impacto discernible en el valor máximo de esfuerzo del tulip frontal (P3). En contraste, los radios de los pernos en el lado exterior (P1) influyen de forma significativa en el valor máximo de esfuerzo del tulip frontal. Al aumentar los radios de los agujeros de perno en el lado exterior de 3 mm a 3,5 mm resulta en un aumento en el valor máximo de esfuerzo (P3); más allá de este punto, aumentos adicionales conducen a una disminución en el valor máximo de esfuerzo.
En la Figura 27 se muestra que los radios de los agujeros de perno en ambos lados frontal (P1) y trasero (P2) del tulip trasero tienen un impacto significativo en el valor máximo de esfuerzo (P3). Inicialmente, a medida que los valores de P1 y P2 aumentan desde 3 mm, el valor máximo de esfuerzo disminuye, alcanzando un mínimo a los 4.5 mm. Sin embargo, aumentos adicionales en los radios de los agujeros de perno incrementan el valor máximo de esfuerzo. Este análisis de sensibilidad revela que el esfuerzo mínimo para el tulip frontal ocurre con un radio de agujero de perno de 5 mm, mientras que para el tulip trasero, un radio de 4,5 mm es óptimo. Estos parámetros de diseño reducen el esfuerzo máximo a 627 MPa y 286 MPa para el tulip frontal y trasero, respectivamente. Los agujeros de perno más grandes contribuyen a un factor de seguridad (FOS) incrementado de 1,33. En consecuencia, la capacidad máxima de carga de la estación alar aumenta de 653 kg a 706 kg con este diseño optimizado. Este análisis de sensibilidad es crucial para optimizar el diseño de las conexiones atornilladas en los tulip, ayudando a identificar el diámetro más adecuado que minimiza las concentraciones de esfuerzos y mejora el rendimiento estructural general de los tulip frontal y trasero.
4. Conclusiones
Este estudio aborda una brecha significativa en la aplicación de investigaciones similares de vanguardia al centrarse en la influencia de las características de rigidez en la capacidad máxima de carga del ala de un avión de combate. Aunque estudios previos han explorado varios factores que afectan la integridad estructural de los componentes de las aeronaves, pocos han profundizado en el papel de la rigidez del ala y su impacto directo en la capacidad de carga. Esta investigación integra la rigidez del ala en el modelo de elementos finitos (FE) de las tulip aisladas, proporcionando un análisis que predice con precisión la integridad estructural de la estación del ala. Además, al utilizar el submodelado como una técnica versátil y eficiente desde el punto de vista computacional, se introduce una metodología innovadora que llena un vacío en la literatura existente al mostrar su aplicabilidad a componentes estructurales complejos con un gasto computacional mínimo.
La validación de la hipótesis inicial mediante los datos obtenidos subraya la importancia de la rigidez del ala en la evaluación de la capacidad máxima de carga de la estación del ala. En conjunto, esta investigación mejora la comprensión del análisis estructural en ingeniería aeroespacial al proporcionar nuevos conocimientos y metodologías para abordar una brecha crítica en el campo. Los principales hallazgos de esta investigación se detallan de la siguiente manera:
Tulip frontal:
• Radio óptimo del agujero del perno: 5 mm
• Reducción máxima del estrés: 627 MPa
Tulip trasero:
• Radio óptimo del agujero del perno: 4,5 mm
• Reducción máxima del estrés: 286 Mpa
Factor de seguridad (FOS):
• Aumentado a 1,33 con agujeros de perno más grandes
Capacidad máxima de carga:
• Aumentada de 653 kg a 706 kg con el diseño optimizado
Identifica parámetros críticos de diseño para optimizar las conexiones atornilladas en las tulip, ayudando a determinar el diámetro más adecuado que minimice las concentraciones de estrés y mejore el rendimiento estructural general tanto de la Tulip frontal como de la Tulip trasero.
Una limitación notable de esta investigación es la exclusión de los sujetadores del análisis, basada en la suposición de una transferencia de carga perfecta entre los elementos estructurales del ala y las tulip del ala. Por lo tanto, este estudio no considera los posibles modos de falla asociados con los sujetadores.
Los futuros esfuerzos de investigación deberían explorar los siguientes aspectos para mejorar la integralidad de los análisis estructurales. Abordar estos aspectos contribuiría significativamente a las evaluaciones estructurales de grandes conjuntos.
Efectos no lineales:
• Implicaciones de los efectos no lineales en la integridad estructural.
Patrones de malla:
• Efectos de los patrones de malla regular en los resultados de simulación.
Carga cíclica / Análisis de densidad espectral de potencia (PSD):
• Análisis de carga cíclica y PSD para evaluar el rendimiento estructural a largo plazo.
Contribuciones del autor
La totalidad de esta investigación, incluida la revisión de literatura, metodología, resultados y conclusiones, representa el trabajo del autor.