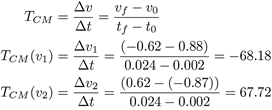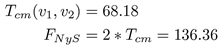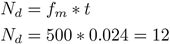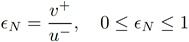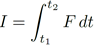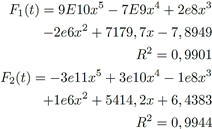1. Introducción
En física resulta importante llevar a cabo experimentos para comprender a fondo los fenómenos que por lo general se dan por hecho en la teoría [1]. En el estudio de la colisión elástica frontal, donde los cuerpos no sufren deformaciones permanentes durante el impacto y no se produce intercambio de masa se separan íntegramente después de la colisión [2], se considera el principio de conservación de la energía cinética y del momento lineal, tanto antes como después del impacto. Sin embargo, se pasa por alto lo que acontece durante el tiempo de contacto entre los objetos que intervienen en la colisión.
Las colisiones entre cuerpos han sido objeto de un amplio estudio en el ámbito de la Física y la caracterización del tiempo de contacto durante dichas colisiones es de particular interés para la presente investigación. Este tiempo, definido como el intervalo instantáneo en el cual los objetos interactúan durante el impacto, desempeña un factor importante en la determinación de las fuerzas y los cambios en las velocidades de los cuerpos de prueba. Por la complejidad inherente a este fenómeno, especialmente en entornos reales, se ha limitado significativamente la capacidad para comprenderlo de manera absoluta.
El tiempo de contacto puede situarse en el orden de centésimas o milésimas de segundo, lo que plantea desafíos considerables para la obtención precisa de datos experimentales.
La creciente incorporación de la tecnología en los laboratorios de Física permite obtener mediciones de los parámetros físicos en intervalos cortos de tiempo, además, permite registrar información de eventos que pasan desapercibidos para el observador, debido a lo rápido que suceden y que con el uso de instrumentos convencionales no se puede lograr [2]. En este contexto, la evolución de los sensores de posición y movimiento desempeña un papel fundamental en el estudio de la colisión de los cuerpos, ya que posibilita la obtención de información de procesos graduales prácticamente instantáneos.
Los equipos actuales disponibles en diversos laboratorios de física incorporan avanzados dataloggers. Estos dispositivos digitales facilitan la conexión de varios sensores para la recopilación de datos, desempeñando un papel integral en la realización de experimentos.
Los dataloggers pueden ser reemplazados por computadores con conectividad Bluetooh para receptar la información de los sensores, que son transductores que tienen la tecnología para detectar magnitudes físicas o químicas, llamadas variables de instrumentación y transformarlas en variables eléctricas [3].
En el mundo real, las magnitudes físicas son inherentemente analógicas, para su procesamiento y utilización en dispositivos digitales, se recurre al convertidor analógico-digital (ADC). Sin embargo, antes de la digitalización, estas magnitudes atraviesan una etapa previa conocida como frecuencia de muestreo. Esta característica determina la cantidad de muestras que se toman por segundo. Un adecuado ajuste de la frecuencia de muestreo garantiza una captura efectiva de la información analógica, evitando pérdidas significativas de datos y permitiendo una conversión más fiel en el proceso de digitalización.
El muestreo, también denominado discretización de señal, es el primer paso en el proceso de conversión de una señal analógica (tiempo y amplitud continuos) en una señal digital (tiempo y amplitud discretos) [4]. Dada esta perspectiva, la implementación de carros con sensores se postula como una alternativa para recrear colisiones elásticas y examinar minuciosamente los eventos que suceden durante el momento de contacto entre los cuerpos.
La utilización de sensores en un entorno real es de importancia al momento de activar los sistemas de seguridad pasivos de los vehículos. En el caso de un impacto, el cinturón de seguridad con pretensor y el airbag son sistemas de seguridad pasiva. Entre los principales elementos del sistema airbag, se encuentra la unidad de control, el sensor de seguridad Safing y el sensor de impacto. El sensor de seguridad Safing está integrado en el módulo airbag y conectado en línea con los sensores de impacto frontal. El sensor de impacto es sensible a la combinación de fuerza, aceleración y tiempo de duración [5]. El sensor de aceleración aporta información de cómo varía la velocidad a la que se mueve el vehículo y el sensor de impacto detecta la fuerza de impacto frontal [6].
El sistema airbag es comandado por la unidad electrónica para su activación, esto lo realiza sobre la base de las señales recibidas por el sensor del sistema que está ubicado estratégicamente para detectar paradas bruscas por causa de una colisión. El airbag entra en acción ante un cambio brusco de la inercia general del vehículo, como sucede en caso de un impacto frontal contra un obstáculo u otro vehículo [7].
La simulación de impacto frontal para el análisis biomecánico mediante elementos finitos permite conocer los beneficios de la implementación de un airbag como elemento de seguridad pasiva [8]. Este enfoque no solo mejora la calidad de la presente investigación, sino que también abre nuevas posibilidades para explorar y validar modelos teóricos en un contexto práctico y dinámico.
El nuevo reto de los laboratorios de física es utilizar de forma efectiva toda la información generada por los sensores para su interpretación y análisis [9]. La interpretación cuidadosa y absoluta de estos datos es fundamental para comprender los fenómenos físicos subyacentes y para validar las teorías existentes o formular nuevas hipótesis. Los datos experimentales proporcionan una base empírica sólida que respalda las conclusiones científicas y permite a los investigadores tomar decisiones informadas sobre el desarrollo de teorías y modelos.
2. Materiales y métodos
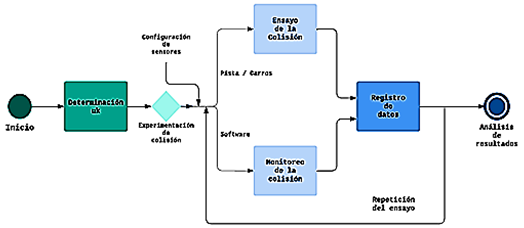
La metodología utilizada en la investigación se sintetiza en la Figura 1. Se muestran las etapas más relevantes de la experimentación.
Para llevar a cabo la experimentación, se determinó el coeficiente de rozamiento dinámico uk entre las llantas delgadas de plástico de los carros y la pista de aluminio, para lo cual, se colocó un carro sobre la pista horizontal y se aumentó el ángulo de inclinación (θ) hasta que el carro comenzó a moverse libremente (θk), denominado ángulo de fricción cinética [10].
Para establecer la ecuación que permite encontrar el coeficiente de rozamiento dinámico se consideraron las fuerzas involucradas en el diagrama de cuerpo libre [11] y el ángulo de inclinación.
La relación matemática que se estableció para determinar este coificiente es uk = tan(θk) [12], se obtuvo del libro de Física de Serway, dando como resultado un coeficiente de rozamiento dinámico experimental de uk = 0, 009.
A continuación, se utilizaron los carros de prueba equipados con sensores inalámbricos en condiciones óptimas y masas aproximadamente iguales (m1 = 0, 5048kg) y (m2 = 0, 5022kg).
Los carros fueron dispuestos de manera frontal sobre la pista de aluminio y separados por una distancia de un metro. Se estableció una conexión entre el sistema Bluetooth de la computadora y los sensores, con el fin de recopilar datos.
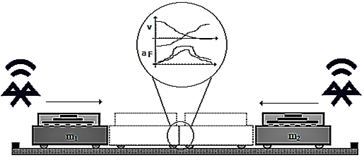
La pista fue instalada de manera tal que no presente desniveles y quede libre de obstrucciones, con el objetivo de minimizar la pérdida de energía cinética (ver Figura 2).
Para proporcionar el impulso inicial a los carros, se utilizaron resortes con características similares y fuerzas equivalentes, los cuales fueron incorporados en la parte posterior de cada carro. Al liberar los resortes, los carros se desplazaron en sentidos contrarios, produciéndose la colisión.
Las experimentaciones permitieron verificar que el tiempo de contacto fue de 0,025 segundos, lo que implica una colisión rápida y potencialmente violenta. Durante esta fracción de tiempo, también se establecieron los valores de las velocidades al inicio y al final del contacto, los cuales representan el promedio de los datos experimentales (Tabla 1).
En este lapso, existen cambios rápidos de la velocidad, por lo tanto, con una frecuencia de muestreo inferior a la mínima requerida se puede llevar a la pérdida de información y a la distorsión de la señal registrada.
Para reconstruir con precisión la señal a partir de los datos muestreados, es esencial que la frecuencia de muestreo sea adecuada.
El teorema de Nyquist-Shannon se puede aplicar a cualquier señal, incluidas las señales polinómicas. Este teorema establece que, para reconstruir una señal de manera precisa a partir de sus muestras, la frecuencia de muestreo debe ser al menos el doble de la frecuencia más alta presente en la señal [13]. En el caso de una señal polinómica, la frecuencia más alta corresponde a la frecuencia de oscilación más alta de la función polinómica. La función polinómica no tiene una frecuencia intrínseca, ya que no se trata de una señal periódica. Sin embargo, su frecuencia más alta puede ser determinada por su tasa de cambio máxima.
La tasa de cambio máxima (TCM) se obtiene al valorar la función de la velocidad en el intervalo de colisión, mediante la ecuación (1).
La tasa de cambio de las funciones velocidad tiene valores considerables de -68,18 y 67,72, sugiriendo que existe una variación rápida. Las tasas de cambio en valor absoluto son semejantes, sin embargo, la mayor tasa de cambio entre estos valores es 68,18. Este valor es referente para aplicar el teorema de Nyquist-Shannon (F NyS ) que sugiere una frecuencia mínima de muestreo como el doble de la tasa máxima de cambio, (ecuación (2)).
La frecuencia mínima necesaria para el muestreo es de 136,36 Hz. Sin embargo, para asegurar una reconstrucción óptima de la señal, se utilizó una frecuencia de muestreo superior a la mínima requerida, en este caso, se estableció una frecuencia de muestreo (fm) de 500 Hz. En un periodo de 0,024 segundos y con una frecuencia de muestreo definida, se lograron registrar doce datos, número de datos (Nd), (ecuación (3)).
Este número de datos es aplicable para la reconstrucción de las señales en discusión, debido a que la experimentación ocurre en un tiempo de 0,024 segundos.
3. Resultados y discusión
En el marco de análisis, se recrearon múltiples colisiones.
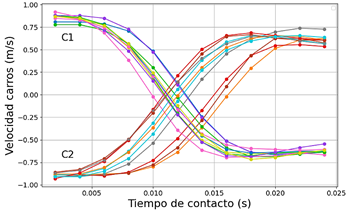
Durante la colisión, los carros de prueba no sufrieron deformaciones permanentes ni variación de masa. Las velocidades fueron monitoreadas de manera continua, registrándose los datos en el intervalo de tiempo. Los múltiples ensayos formaron patrones y valores similares de velocidad durante el tiempo de contacto (ver Figura 3).
Al observar el tiempo inicial n la Figura 3, los móviles tienen velocidades promedio con magnitudes de 0,88 m/s y -0,87 m/s, respectivamente. Las velocidades tienen signos opuestos, indicando que los móviles se mueven en sentidos contrarios. A medida que avanza el tiempo, las velocidades de ambos móviles disminuyen.
Esto indica que existe una fuerza de frenado que actúa sobre los carros en contacto. Alrededor de los 0,014 segundos, las velocidades cambian de signo para los dos carros. Esto indica un cambio en el sentido del movimiento. De los 0,014 segundos en adelante, las velocidades de los carros continúan variando, pero con magnitudes y sentidos diferentes; el carro 1 tiene velocidades negativas, el carro 2 tiene velocidades positivas lo que indica que se están moviendo en sentidos opuestos a la inicial. A los 0,024 segundos se observa que las velocidades de los carros han disminuido en magnitud, por la presencia de fuerzas disipativas como la fuerza de rozamiento, cuyo efecto es la pérdida de energía.
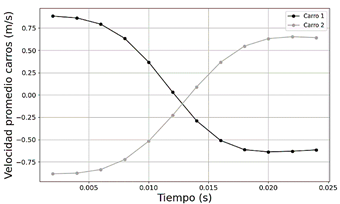
Para identificar las funciones matemáticas que se ajusten de manera óptima a los datos, se llevó a cabo un análisis de regresión. A través de este proceso, se determina que la función polinómica de grado 5 es la más adecuada para modelar la información disponible. Las experimentaciones en un ambiente controlado pueden estar sujetas a variaciones y errores inherentes, como errores de medición o condiciones físicas de los instrumentos utilizados. Sin embargo, la reproducción de datos semejantes obtenidos en las experimentaciones, sugiere que los datos son consistentes. En este sentido, promediar las velocidades durante el tiempo de contacto, ayuda a minimizar el impacto de estos errores en el análisis (ver Figura 4).
3.1. Cinemática del carro 1
La Figura 5 representa la variación de la velocidad en el tiempo de contacto en la colisión. La función matemática que se ajusta al comportamiento de esta variación, es polinómica de grado 5, v(t) = −5E9t5 + 3E8t4 − 5E6t3 + 28990t2 − 66, 985t + 0.9339.
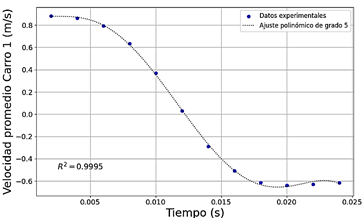
Figura 5 Variación de velocidad en función del tiempo del carro 1, durante el tiempo de contacto en la colisión
Para el ajuste de curva se obtiene un coeficiente de determinación R2 = 0, 9995. Un valor de coeficiente cerca de la unidad indica un ajuste fuerte del modelo a los datos. Prácticamente, el 99,95 % de la variabilidad en los datos se presenta mediante la relación en la función polinómica.
En t = 0, 002[s], la velocidad inicial del carro es 0, 88[m/s]. Desde t = 0, 002[s] hasta t = 0, 012[s], la velocidad disminuye, pasando de 0, 88[m/s] a 0, 03[m/s].
A partir de 0,012 segundos, la velocidad varía de positiva a negativa, indicando un cambio de sentido del movimiento. Después del cambio de sentido, la velocidad aumenta en magnitud, llegando a −0, 64[m/s] en t = 0, 020[s]. A partir de los 0,020 segundos, la velocidad tiende a estabilizarse alrededor de −0, 64[m/s].
3.2. Cinemática del carro 2
La función matemática que se ajusta al comportamiento de la variación de la velocidad del carro 2 (ver Figura 6), también es polinómica de quinto grado, v(t) = 4E9t5 − 3E8t4 + 6E6t3 − 43570t2 + 135, 4t − 1, 023.
El coeficiente de determinación R2, para el ajuste de curva es de 0,9999. El valor de R2 indica un ajuste fuerte del modelo a los datos. Prácticamente, el 99,99 % de la variabilidad en los datos de la variable dependiente se explica mediante la relación en la función polinómica.
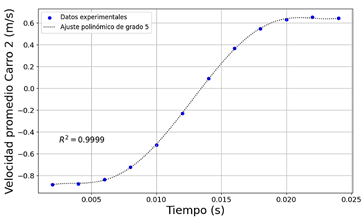
Figura 6 Variación de velocidad en función del tiempo del carro 2, durante el tiempo de contacto en la colisión
En t = 0,002 [s], la velocidad inicial del carro es -0,87 [m/s]. El signo negativo indica que el carro se está moviendo en el sentido opuesto al elegido. La velocidad disminuye desde -0,87 [m/s] hasta -0,22 [m/s] en 0,012 segundos. Luego, la velocidad cambia de sentido y comienza a aumentar. En 0,014 segundos, la velocidad es 0,09 [m/s], indicando que el carro ha cambiado de sentido y ahora se está moviendo en el sentido opuesto. Después del cambio de sentido, la velocidad aumenta de manera constante hasta 0,63 [m/s] en 0,024 segundos.
3.3. Coeficiente de restitución
Para el análisis del coeficiente de restitución se considera la ley cinemática de impacto de Newton (ϵn) a través de la ecuación (4), [14].
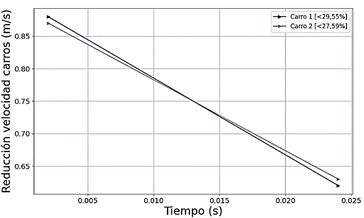
Donde el coeficiente de restitución es el cociente entre las velocidades relativas de la colisión en el instante del contacto y separación como manifiesta la literatura [15] , (ver Figura 7).
En consecuencia, la magnitud de la velocidad promedio al finalizar el contacto (v1 = 0, 64) del carro 2, disminuyó en 29,55 % en comparación a la magnitud de la velocidad promedio al contacto (u1 = −0, 88).
La magnitud de la velocidad promedio al finalizar el contacto (v2 = −0, 61) del carro 1, disminuyó en 27,59 % en comparación a la magnitud de la velocidad promedio al iniciar el contacto (u2 = 0, 88), en estas condiciones el coeficiente de restitución de la experimentación calculado a través de la ecuación (4), resulta ser ϵN = 0,712.
Un coeficiente de restitución menor a 1 y superior a 0, revela que la colisión es parcialmente elástica, lo que significa que parte de la energía cinética se pierde durante la colisión en forma de calor, sonido, deformación u otras manifestaciones de energía no cinética.
3.4. Fuerzas impulsivas
La variación de las velocidades en una impulsión se produce en un intervalo muy breve (Δt), asociado a una fuerza de tipo impulsivo de valor máximo elevado [16]. En la teoría de impulsiones se adopta la hipótesis de que la duración del intervalo de impulsión es breve, pudiendo considerarse el fenómeno como prácticamente instantáneo. En física, el impulso o impulsión se define como la variación de la cantidad de movimiento de un objeto y está relacionada con la fuerza (F) y el diferencial del tiempo (dt) durante el cual actúa esa fuerza [16]. Ver ecuación (5)
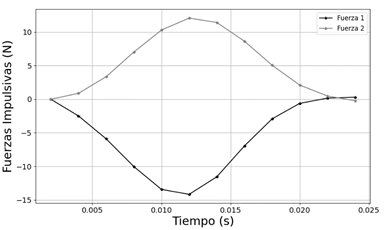
Las fuerzas impulsivas son las responsables de cambiar las velocidades de los carros en la colisión. La experimentación permite calcular las fuerzas impulsivas en el tiempo de contacto, mediante la segunda ley de Newton, y no asumir la hipótesis de que el fenómeno es instantáneo. En la Figura 8 se observan las fuerzas impulsivas en acción, en el instante de contacto 0,022 segundos. Estos fenómenos físicos pueden ser modelados mediante funciones polinómicas que permiten describir el comportamiento del sistema con precisión y predecir su evolución durante el tiempo de contacto.
Las fuerzas impulsivas, que actúan sobre los carros 1 y 2, muestran comportamientos diferentes a lo largo del tiempo, la fuerza 1 y la fuerza 2 son contrarias, la variación de la magnitud de la fuerza 1 es mayor en comparación con la fuerza 2.
Los ajustes de curva para las fuerzas impulsivas de los carros 1 y 2 se realizaron bajo el criterio del valor del coeficiente de determinación R2, cercano a 1 tiene un mejor ajuste.
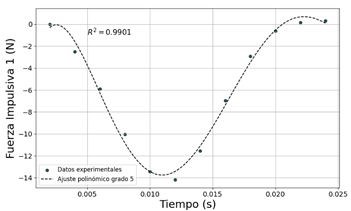
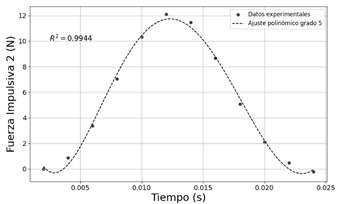
El ajuste de curva para la fuerza impulsiva 1 (Figura 9) y la fuerza impulsiva 2 (Figura 10), se obtienen a través de la función polinómica de grado 5:
En la Figura 9 se observa que la fuerza de impacto del carro 1 alcanzó el máximo valor FI1 = −14, 171[N] en un tiempo relativamente corto tI1 = 0, 012[s], lo que indica una transferencia rápida de energía entre los objetos en colisión.
En la Figura 10 se observa que la fuerza de impacto del carro 2 alcanzó el máximo valor FI2 = 12, 097[N] en un tiempo relativamente corto tI2 = 0, 012[s].
El tiempo promedio en el que las fuerzas impulsivas alcanzan su valor máximo es de 0,012 segundos.
En un escenario real de impacto, este tiempo resulta concluyente, ya que la magnitud máxima de la fuerza estaría presente durante ese intervalo. En consecuencia, al considerar un entorno real, establecer un tiempo de reacción para un airbag menor a los 0,012 segundos se convertiría en un aspecto fundamental de la seguridad a tener en cuenta. La implementación de un tiempo de reacción pertinente en los sistemas de airbags permitiría mitigar los efectos de las fuerzas de impacto y, así, reducir el riesgo de lesiones para los ocupantes de un vehículo.
4. Conclusiones
El conocimiento de la variación de la velocidad, de las fuerzas impulsivas y del tiempo de contacto en una colisión, es esencial para la optimización de sistemas de retención, como cinturones de seguridad y sistemas de activación de airbags. Esto ayuda a garantizar que estos sistemas proporcionen la máxima protección durante una colisión en el instante adecuado. Tal como lo dice Guazhambo y Larrea, en su tesis de grado de la Universidad Politécnica Salesiana, titulada “Base de datos de funcionamiento del airbag en los vehículos que realizan la RTV en la ciudad de Cuenca, determinando el cumplimiento de la RTE INEN 034”.
Los modelos teóricos pueden sugerir colisiones perfectamente elásticas con un coeficiente de restitución de 1, en la práctica, siempre hay factores del mundo real que afectan a las colisiones y contribuyen a deformaciones imperceptibles, fricción y pérdida de energía. Estos factores hacen que sea difícil, e incluso imposible, alcanzar un coeficiente de restitución de 1 en experimentos de laboratorio. La búsqueda de modelos más realistas y la comprensión de las fuentes de pérdida de energía son esenciales para interpretar y aplicar los resultados experimentales.
A través de esta investigación se ha llegado a modelar las funciones de velocidad-tiempo y fuerza-tiempo como funciones polinómicas de grado 5, que representan la variación de velocidades y fuerzas en 25 milisegundos, indicando un comportamiento no lineal, crecimiento y decaimiento acelerado. Comprender la cinemática de la colisión a esta escala, incluyendo la velocidad relativa, la fuerza de impacto y la duración del contacto, puede ayudar a detectar cuándo ocurre una colisión y cuándo se presenta el valor pico de las fuerzas impulsivas y cuándo deben activar los sistemas de seguridad pasivos.
Al analizar y comprender procesos de interacciones dinámicas se estaría explorando conceptos de nanotecnología, donde los procesos físicos y químicos suceden a escalas infinitesimales. Por tal razón, para trabajos futuros se debería analizar la posibilidad de utilizar modelos matemáticos en la simulación y análisis de procesos físicos a nano escala con el objetivo de anticipar el comportamiento de la velocidad y fuerza en periodos temporales más extensos y comparar los resultados con datos experimentales. También sería importante explorar, a qué variables representan cada uno de los coeficientes de las funciones de velocidad y fuerza. En el ámbito educativo, el análisis experimental de la cinemática en la colisión elástica entre dos cuerpos durante el tiempo de contacto, capacita a los estudiantes para aplicar conceptos teóricos de una manera práctica, lo que mejora su comprensión y valoración por la física.