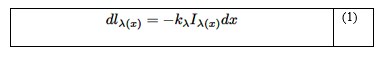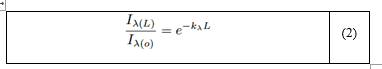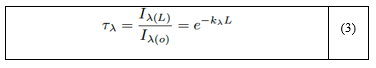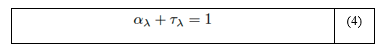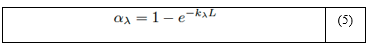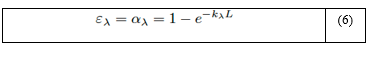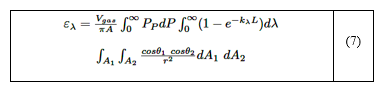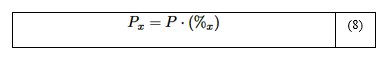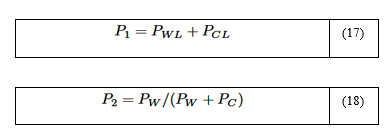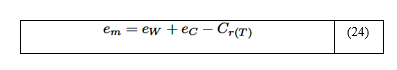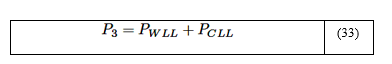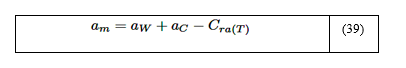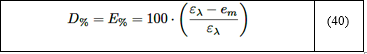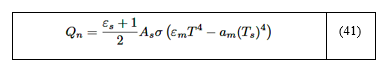Introducción
En el intercambio térmico por radiación entre superficies, en muchas ocasiones para simplificar el análisis es admitido que ambas superficies están separadas por un medio no participante, o sea, que no emite, dispersa o absorbe la radiación. El aire atmosférico a temperaturas y presiones comunes se aproxima mucho a un medio no participante. Los gases que están compuestos por moléculas monoatómicas, como el helio y el argón, o de moléculas biatómicas simétricas, como el O2 y el N2 muestran un comportamiento cercano a un medio no participante, excepto a temperaturas extremadamente elevadas en las cuales ocurre la ionización. Por esta razón, en los cálculos relativos a la radiación ejecutados en la práctica, el aire atmosférico es considerado como un medio no participante [1-3].
Los gases con moléculas asimétricas, como el SO2,CO,H2O,CO2, y los hidrocarburos CmHn, a temperaturas moderadas pueden absorber energía en los procesos de transferencia de calor por radiación, mientras que a temperaturas elevadas, como las que se encuentran en las cámaras de combustión, pueden emitir y absorber simultáneamente. Por lo tanto, en cualquier medio que contenga ese tipo de gases en concentraciones suficientes, debe ser tenida en cuenta la influencia del medio participante en los cálculos relativos a la radiación. Los gases de la combustión en un horno o cámara contienen cantidades suficientes de H2O y CO2, por tanto, la evaluación térmica del mismo debe incluir el efecto participante de los gases [4, 5].
La presencia de un medio participante complejiza el análisis del intercambio térmico debido a la radiación. El medio participante absorbe y emite radiación en todo su volumen, de esta forma, la radiación gaseosa es un fenómeno volumétrico y, por tanto, depende del tamaño y de la forma del cuerpo, incluso si la temperatura fuese uniforme en todo el medio. Los sólidos emiten y absorben radiación sobre todo el espectro; sin embargo, los gases emiten y absorben energía en varias bandas angostas de longitudes de onda. Esto indica que, la hipótesis de considerar un cuerpo gris no siempre resulta ser apropiada para un gas, incluso cuando las superficies circundantes sean grises. Las características individuales de absorción y emisión de los gases que componen una mezcla, también dependen de la presión, temperatura y composición de esa mezcla. Por tanto, la presencia de otros gases participantes afecta las características de radiación de un gas en particular, debido al solapamiento de las bandas de emisión de cada gas componente de la mezcla [6-8].
En un gas, la distancia entre las moléculas y la movilidad es mayor que en los sólidos, lo cual propicia que una parte importante de la radiación emitida por las partes profundas llegue al contorno de delimitación de la masa. Las capas gruesas de un gas absorben más energía y transmiten menos que una capa delgada. Esto ocasiona que, además de detallar las propiedades que fijan el estado del gas (temperatura y presión), también es requerido especificar una longitud característica L de la masa del gas antes de determinar sus propiedades radiativas, siendo dado el poder emisivo y el absorbente como una función de la longitud L que debe recorrer la radiación en la masa. Por tanto, en los gases el poder emisivo ε es una función del producto de la presión parcial del gas Px y de la longitud característica del haz de radiación L [9-11].
La propagación de la radiación a través de un medio participante se puede complejizar debido al efecto simultáneo de aerosoles, como el polvo, las partículas de hollín (carbón no quemado), las gotitas de líquido y las partículas de hielo, las cuales dispersan la radiación. La dispersión se refiere al cambio de dirección de la radiación debido a la reflexión, refracción y difracción. La dispersión causada por las propias moléculas de gas se conoce como dispersión de Rayleigh y tiene un efecto despreciable sobre la transferencia de calor. Un estudio de avanzada sobre el intercambio térmico por radiación en medios dispersantes es abordado por varios investigadores [12-14].
La evaluación del intercambio térmico por radiación a través de medios participantes ha sido objeto de estudios durante décadas. Uno de los métodos más difundidos y recomendados en la literatura especializada es el método gráfico de Hottel (MGH), el cual proporciona una desviación media de ±25 %. El MGH se basa en la lectura e interpretación de nomogramas experimentales, lo cual introduce errores adicionales, debido a la lectura visual de gráficos, por tal motivo en muchos casos la desviación real puede computar valores superiores a ±35 %, lo cual es una limitante importante en su uso [15, 16].
Desde el punto de vista matemático, el tratamiento analítico del problema resulta sumamente complejo, pues se requiere primeramente definir la solución analítica del factor de visión, para posteriormente realizar una integración volumétrica (puede simplificarse utilizando las ventajas del cálculo vectorial). Es lógico que el tratamiento matemático requerido involucre el manejo de un grupo elevado de funciones primitivas, las cuales en muchas ocasiones requieren del uso de métodos numéricos para la solución de funciones especiales, que son obtenidas en contornos con características cilíndricas o esféricas (funciones de Bessel, Spence y Godunov). Por esta razón, en la actualidad no se dispone de una SA para este tipo de problemas, los cuales son por lo general abordados por métodos aproximados en su mayoría derivados del método de Montecarlo y del uso de técnicas numéricas y el método de elementos finitos [17-19].
Aunque los medios participantes pueden ser también líquidos o sólidos semitransparentes, como el vidrio, agua y los plásticos, este trabajo se limita a los gases que emiten y absorben radiación. En particular se considerará la emisión y absorción de radiación solo por el H2O y CO2, dado que son los gases participantes que se encuentran con mayor frecuencia en la práctica, pues los productos de la combustión en los hornos y las cámaras de combustión en los que se queman hidrocarburos contienen los tres gases en concentraciones elevadas [20-22].
Por tanto, el objetivo principal de este trabajo es obtener una solución aproximada para evaluar el intercambio térmico por radiación a través de un medio participante gaseoso compuesto por H2O y CO2, que no muestre una elevada complejidad matemática y que garantice, además, un margen de error con respecto a la SA que se considere adecuado para el uso en ingeniería (±15 %). En este trabajo también serán obtenidas las SA para determinar el valor de L en diversas combinaciones geométricas de superficies de uso extendido en ingeniería, así como la emisividad y absortividad de la mezcla gaseosa participante.
Para establecer comparaciones fueron calculadas las soluciones analíticas de 355 combinaciones de temperatura termodinámica en el rango 300K ≤ T ≤ 2100K y del producto de la presión total de la mezcla de gases y la longitud característica del haz de radiación (PL) en el rango 0, 06 atm · m ≤ PL ≤ 20 atm · m. Para cada juego de valores PL ;T es calculado el valor de emisividad y absortividad espectral exacta ελ y aλ para la mezcla de gases mediante la SA y el valor de la emisividad y absortividad de la mezcla εm y am , usando el MGH y la solución aproximada propuesta.
Dado el carácter práctico de la contribución y los valores razonables de los ajustes obtenidos, la propuesta es una herramienta adecuada para su aplicación a la ingeniería térmica y prácticas afines que requieren cálculos de radiación térmica a través de medios participantes.
Materiales y métodos
Propiedades relativas a la radiación en un medio participante
Considérese un medio participante de espesor determinado. Sobre el medio incide un haz de radiación espectral de intensidad Iλ(0) , el cual es atenuado conforme se propaga debido a la absorción. La disminución en la intensidad de la radiación a medida que pasa a través de una capa de espesor dx es proporcional a la propia intensidad y al espesor dx. Esto se conoce como ley de Beer y se expresa como [23]:
Donde: kλ - coeficiente de absorción espectral del
medio.
Separando variables en la ecuación (1) e integrando entre los límites x=0 hasta x=L se obtiene [13]:
En la deducción de la ecuación (2) se ha supuesto que la absortividad del medio es independiente de x, considerando que la decrece en forma exponencial. La transmisividad espectral de un medio se puede definir como la razón entre la intensidad de la radiación que sale del medio y la que entra en este; es decir:
La transmisividad espectral τλ de un medio representa la fracción de la radiación transmitida por ese medio a cierta longitud de onda. La radiación que pasa a través de un medio no dispersante (y por ende, no reflector) es absorbida o transmitida. Por lo tanto, se cumple que [12]:
Combinando las ecuaciones (3) y (4) es obtenida la absortividad espectral de un medio de espesor L la cual viene dada por la ecuación (5):
Siguiendo el principio de la ley de Kirchoff, la emisividad espectral es dada por la ecuación (6):
Por tanto, la absortividad, transmisividad y emisividad espectrales de un medio son valores adimensionales, cuyos valores son iguales o menores que la unidad. Los coeficientes ελ, αλ y τλ varían con la longitud de onda, la temperatura, la presión y la composición de la mezcla [12].
Longitud media del haz de radiación
La emisividad y absortividad de un gas va a ser dependiente de la longitud característica y de la forma y el tamaño de la masa gaseosa que interviene. Durante sus experimentos en la década de 1930, Hottel y sus colaboradores consideraron que la emisión de radiación va desde una masa hemisférica de gas hacia un pequeño elemento de superficie ubicado en el centro de la base del hemisferio. Por tanto, resulta conveniente extender los datos de la emisividad de los gases estudiados por Hottel hacia masas de gases con otras configuraciones geométricas, y esto se lleva a cabo mediante la introducción del concepto de longitud característica o media del haz L, la cual representa al radio de un hemisferio equivalente [24-26].
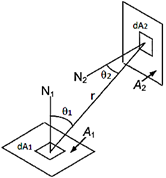
La SA, que permite obtener la emisividad espectral de la mezcla gaseosa participante, es una función del producto de la longitud L, la presión parcial del componente participante y el factor de visión entre las superficies emisora y receptora (véase la Figura 1), siendo descrito mediante la ecuación (7) [27]:
Donde: A1 y A2 son las superficies emisoras y receptoras. θ1,θ2: ángulos entre el vector normal a las áreas dA1 y dA2 y la línea que conecta el centro de las superficies A1 y A2 · A, Vgas: área total de las superficies calefactoras y el volumen del recinto. r es la distancia entre el centro de las superficies A1 y A2 .
La ecuación (7) es muy compleja para ser usada en cálculos prácticos de ingeniería, por tal motivo en múltiples ocasiones se acude a simplificaciones o aproximaciones [28].
Resolver la ecuación (7) es una tarea compleja, fundamentalmente por la elevada cantidad de funciones primitivas e integrales inmediatas a ser manipuladas en el proceso de integración. Por esta razón, en la literatura especializada para determinar los valores de L son conocidas SA para casos puntuales [29], mientras que para otras configuraciones comunes solo se disponen de valores aproximados obtenidos de forma experimental [30].
Emisividad y absortividad de gases participantes y mezclas de ellos
Las propiedades radiativas (PR) en un sólido opaco no dependen de la forma o configuración del mismo, sin embargo, la forma geométrica de un gas sí afecta sus PR. La absortividad espectral del CO2 se compone de cuatro bandas de absorción, posicionadas sobre las longitudes de onda de 1, 9μm, 2, 7μm,4,3μm,15μm [31].
Los mínimos y máximos de esta distribución, así como sus discontinuidades, muestran que las bandas de absorción de un gas se diferencian apreciablemente a las de un cuerpo gris. El ancho y la forma de las bandas de absorción varían con la presión y la temperatura; además, el espesor de la capa de gas también ejerce una importante influencia. Por lo tanto, para la estimación de las PR de un gas, es requerido considerar estos tres parámetros [32].
La absorción y emisión en gases no se realiza de forma continua sobre todo el espectro. Las PR son más significativas en varias bandas con diferentes longitudes de onda y tienden a cero en otras bandas contiguas. En una mezcla gaseosa se complejiza aún más la predicción de las PR, debido al traslape de las bandas espectrales de los diferentes gases que componen la mezcla, por tanto, esta es la causa fundamental que en la actualidad no se dispongan de soluciones analíticas para la estimación de las PR [33].
En la ingeniería térmica, para estimar las PR en una mezcla gaseosa se ha generalizado un método aproximado dado por Hottel. El mismo consiste en evaluar de forma individual cada componente gaseoso que integra la mezcla y posteriormente corrigiendo este valor considerando la influencia de la presión parcial, la temperatura y el solapamiento de las bandas espectrales de los elementos componentes de la mezcla [29].
Este principio permite predecir la emisividad o absortividad de una mezcla de gases con una desviación máxima de ±25 %. Sin embargo, el método de Hottel tiene el gran inconveniente que se fundamenta en la lectura e interpretación de resultados gráficos, lo cual introduce errores adicionales, por lo que los valores de PR estimados pueden computar una desviación media de ±35 % e incluso superior [34].
La presión parcial Px de cada componente en una mezcla de gases viene dado por la siguiente relación [34]:
Donde: P es la presión total de la mezcla de gases.%c es la fracción porcentual de cada gas en la composición total. Se aclara que 1 atm = 105 N/m2.
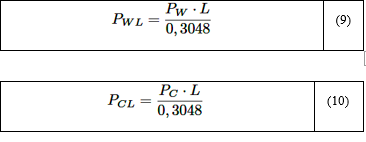
En lo adelante será utilizado el subíndice w y c para referirse al H2O y CO2, respectivamente. Las presiones parciales reducidas para el H2O y CO2 vienen dadas por:
Donde: PW y PC son las presiones parciales del H2O y CO2, respectivamente; L, la longitud característica del haz de radiación.
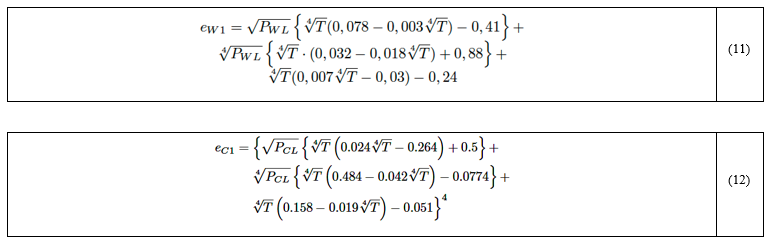
Para una presión unitaria de 1 atm, las emisividades básicas del H2O y CO2 vienen dadas por las ecuaciones (11) y (12).
En las ecuaciones (11) y (12) la temperatura del gas T es dada en K. Si se cumple que P≠ 1 atm, entonces las emisividades básicas del H2O y CO2 computadas con las ecuaciones (11) y (12) deben ser corregidas. Los factores de corrección son obtenidos por las siguientes relaciones:
 Por tanto, cuando P≠ 1 atm, las emisividades del H2O y CO2 vienen dadas por:
Por tanto, cuando P≠ 1 atm, las emisividades del H2O y CO2 vienen dadas por:
Las emisividades obtenidas con el uso de las ecuaciones (15) y (16) corresponden a las fracciones individuales gaseosas de H2O y CO2, respectivamente.
Para determinar la emisividad total es requerido determinar un coeficiente de corrección que considere el efecto del traslape de las bandas de emisión. Este factor de corrección es dependiente de la temperatura y de las presiones parciales del H2O y CO2. Para definir el factor de corrección se establecen dos combinaciones con las presiones parciales, la suma de presiones parciales y la desviación de presiones parciales, las cuales quedan definidas por las relaciones siguientes: 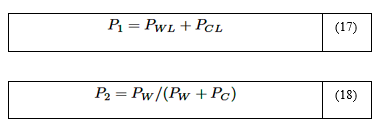
El factor de corrección es obtenido mediante la integración directa de la ecuación (17). El procedimiento matemático es en extremo complejo, razón por la cual acá solamente serán dados los factores de corrección para tres valores prefijados de temperaturas, T=400 K,T=800 K y T ≥ 1200 K, los cuales vienen dados por:
Para valores de temperaturas situados en los intervalos 400K < T < 800K y 800K < T < 1200K, el factor de corrección Cr(T) será determinado mediante la interpolación lineal de Newton, usando las siguientes relaciones:
Conocido el factor de corrección Cr(T) de la mezcla, entonces la emisividad efectiva de la mezcla em viene dada por la siguiente ecuación:
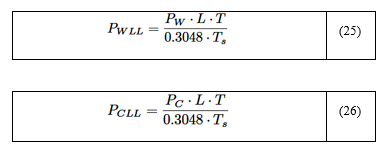
Para determinar la absortividad de los gases es requerido modificar las presiones parciales reducidas, dado que la temperatura de referencia en este caso corresponde a la fuente (emisor o pared), por tanto, las ecuaciones (9) y (10) son transformadas de la siguiente manera:
Donde: Ts corresponde a las temperaturas de las superficies emisoras.
Para una presión unitaria de 1 atm, las absortividades básicas del H2O y CO2 vienen dadas por:
En las ecuaciones (27) y (28) la temperatura de la superficie emisora Ts es dada en K.
Si se cumple que P≠ 1 atm, entonces los valores de absortividades básicas para el H2O y CO2 deben ser modificados, u tilizando para este propósito los factores de corrección calculados con las ecuaciones (13) y (14), y un factor termodinámico que tiene en cuenta la no uniformidad de la distribución de las temperaturas en la superficie emisora y en el seno del gas. Matemáticamente esto queda de la forma siguiente:
Por tanto, cuando P≠ 1 atm, las absortividades del H2O y CO2 vienen dadas por:
Las absortividades calculadas mediante las ecuaciones (31) y (32) corresponden a las fracciones individuales gaseosas de H2O y CO2, respectivamente.
Para calcular la absortividad total es requerido determinar un coeficiente de corrección que considere el efecto del traslape de las bandas de absorción. Este factor de corrección depende de la suma de las presiones parciales reducidas del H2O y CO2, la cual es obtenida mediante la siguiente relación:
El factor de corrección es obtenido mediante la integración directa de la ecuación (7). Dado el elevado grado de complejidad de este proceso de integración, acá solamente serán proporcionados los factores de corrección para tres valores prefijados de temperaturas, T = 400K,T = 800K y T ≥ 1200K, los cuales vienen dados por:
En las ecuaciones (34) a la (36), la desviación de presiones parciales P2 es calculada usando la ecuación (18). Para valores de temperaturas situados en los intervalos 400K < T < 800K y 800K < T < 1200K, el factor de corrección Cra(T) será determinado mediante la interpolación lineal de Newton, usando las siguientes relaciones:
Conocido el factor de corrección Cra(T) de la mezcla, entonces la absortividad efectiva de la mezcla am viene dada por la siguiente ecuación:
Resultados y discusión
Validación del modelo propuesto
Para la validación del modelo propuesto son usados valores aleatorios de temperaturas en el rango 300K ≤ T ≤ 2100K, y seis valores prefijados del producto PL (0.06,0.6,3,5,10,20) atm⁄m, con 55, 55, 45, 55, 45 y 80 datos para cada intervalo PL, respectivamente. Para cada combinación (PL ;T) es calculado el valor de emisividad espectral exacta ελ mediante la SA, y el valor de la emisividad de la mezcla em, usando el MGH y la ecuación (24).
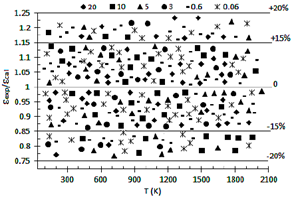
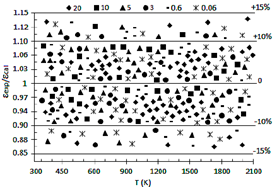
En la Figura 2 es correlacionado el cociente ελ/em y la temperatura T, ajustados en bandas de error de ±15 % y ±20 %, siendo utilizados los valores de em obtenidos mediante el MGH, mientras que en la Figura 3 es correlacionado el cociente ελ/em y la temperatura T, ajustados en bandas de error de ±10 % y ±15 %, usando los valores de em calculados mediante la ecuación (24).
El porciento de desviación (error) es computado con respecto a la SA y es obtenido mediante la siguiente relación [35]:
La Figura 2 muestra que el MGH proporciona el peor ajuste con respecto a la SA, con errores medios de ±15 % y ±20 % para el 54,2 % y 75,3 % de los puntos (PL ; T) evaluados. Para el MGH el mejor ajuste es obtenido para PL=3,0, con errores medios de ±15 % y ±20 % para el 63,2 % y 84,2 % de los datos evaluados, mientras que el peor ajuste es obtenido para PL=10, con errores medios de ±15 % y ±20 % para el 42,7 % y 57,1 % de los datos evaluados.
La Figura 3 muestra que la ecuación (24) proporciona el mejor ajuste con respecto a la SA, con errores medios de ±10 % y ±15 % para el 79,4 % y 94,9 % de los puntos (PL ; T) evaluados. Para la ecuación (24) el mejor ajuste es obtenido para PL=20, con errores medios de ±10 % y ±15 % para el 83,2 % y 98,6 % de los datos evaluados, mientras que el peor ajuste es obtenido para PL=0,6, con errores medios de ±10 % y ±15 % para el 75,1 % y 91,9 % de los datos evaluados.
Aplicación a un caso de estudio
Un horno presurizado, con dimensiones (largo × ancho × alto) igual a (3 m × 4 m × 5 m) contiene gases de combustión a T=1200 K y una presión P=2 atm, mientras que la temperatura de la superficie de las paredes del horno Ts = 1100K. Mediante análisis volumétrico se determina que la composición de los gases de combustión es 87 % de N2,8% de H2O y 5 % de CO2. Es requerido calcular el calor transferido entre los gases de combustión y las paredes del horno, (ladrillo con la superficie gris, satinada).
Utilizando las relaciones dadas en [29] se determina que L = 3, 04m ≈ 3m. Mediante la ecuación (8) son obtenidas las presiones parciales del H2O y CO2, computando PW = 0, 16 y PC = 0, 1, respectivamente. Las presiones parciales reducidas son calculadas mediante las ecuaciones (9) y (10), obteniéndose PWL = 1, 575atm ·m y PCL = 0, 984atm ·m. Las emisividades básicas para el H2O y CO2 son obtenidas usando ecuaciones (11) y (12) respectivamente, siendo eW1 = 0, 255 y eC1 = 0, 135.
Como P≠ 1atm, entonces los valores de emisividades básicas del H2O y CO2, deben ser corregidas mediante las ecuaciones (13) y (14), respectivamente, obteniendo CW = 1, 379 y CC = 1,166. Las emisividades reales del H2O y CO2 son determinadas a través de las ecuaciones (15) y (16), obteniéndose que eW = 0, 3524 y eC = 0, 157. Se calculan la suma P1 y desviación P2 de presiones parciales, usando las relaciones (17) y (18), respectivamente, obteniendo P1 = 2, 559atm · m y P2 = 0, 615atm · m.
La temperatura de la mezcla de gases es 1200 K, por tanto, el coeficiente de corrección Cr(T=1200K) se estima utilizando la ecuación (21), Cr(T=1200K) = 0, 052atm · m. La emisividad efectiva de la mezcla em viene dada por la ecuación (24), donde em = 0, 458. Usando la ecuación (7), tras un engorroso proceso de integración es obtenido el valor exacto de ελ = 0, 463, mientras que el MGH proporciona un valor de em = 0, 43. Mediante la ecuación (40), es determinado el error con respecto a la SA, siendo D% = 1, 08% y D% = 7.13%, para la ecuación (24) y el MGH, respectivamente.
Las presiones reducidas modificadas son obtenidas mediante las ecuaciones (25) y (26), obteniéndose PWLL = 1, 718atm·m y PCLL = 1, 073atm·m. Las absortividades básicas para el H2O y CO2 son calculadas mediante las ecuaciones (27) y (28) respectivamente, siendo aW1 = 0, 275 y aC1 = 0, 144.
Como P ̸= 1atm, entonces las absortividades básicas del H2O y CO2, deben ser corregidas mediante las ecuaciones (29) y (30), respectivamente, obteniendo CWa = 1, 434 y CCa = 1, 234. Las absortividades de las fracciones de H2O y CO2 son determinadas usando las ecuaciones (31) y (32), obteniéndose que aW = 0, 394 y aC = 0, 178. Se calcula la suma de presiones parciales P3 usando la ecuación (33), obteniéndose que P3 = 2, 791atm · m.
La temperatura de la mezcla de gases es 1200 K, por tanto, el coeficiente de corrección Cra(T=1200K) se estima utilizando la ecuación (36), Cra(T=1200K) = 0, 053atm·m. La absortividad efectiva de la mezcla am viene dada por la ecuación (39), donde am = 0, 519. Usando las ecuaciones (6) y (7), tras un tedioso manejo de integrales inmediatas, es obtenido el valor exacto de a = 0, 525, mientras que el MGH proporciona un valor de am = 0, 449. Utilizando la ecuación (40), es determinado el error computado con respecto a la SA, siendo D% = 1, 14% y D% = 14, 48%, para la ecuación (24) y el MGH, respectivamente.
Las paredes del horno son de ladrillo, con una superficie gris (satinada) a una temperatura media TS = 1100K. Con estas características la emisividad normal de la superficie es es = 0, 75.
El flujo de calor intercambiado entre los gases y la pared del horno viene dado por:
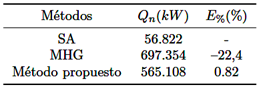
Los valores del flujo de calor intercambiado (en kW) son obtenidos mediante el uso de la SA, el MGH y la ecuación (24), siendo determinado además el error computado con respecto a la SA. En la Tabla 1 son resumidos los valores de flujo de calor (en kW) obtenidos y el error cometido E% en cada caso con respecto a la SA.
Conclusiones
A partir de la comparación de SA, es obtenido un método aproximado para estimar el intercambio térmico por radiación a través de medios participantes. Los modelos propuestos fueron verificados por comparación con las SA disponibles.
Para el MGH y el método propuesto, los modelos obtenidos correlacionan con la totalidad de los datos experimentales con una desviación media de ±20 % y ±10 %, respectivamente.
Para el MGH el peor ajuste con respecto a la SA es obtenido para PL=10, con un error medio de ±20 % para 57,1 % de los datos evaluados, mientras que el mejor ajuste es obtenido para PL=3,0, con un error medio de ±15 % para el 63,2 % de los datos evaluados. Para el método propuesto el peor ajuste con respecto a la SA es obtenido para PL=0,6, con un error medio de ±15 % para 91,9 % de los datos examinados, mientras que el mejor ajuste es obtenido para PL=20, con un error medio de ±10 % para el 83,2 % de los datos evaluados.
En todos los casos, el acuerdo del modelo propuesto con los datos experimentales disponibles es lo suficientemente bueno como para ser considerado satisfactorio para diseño práctico.