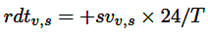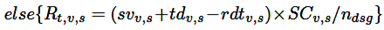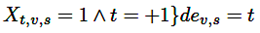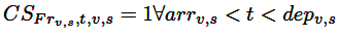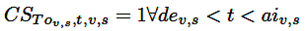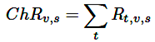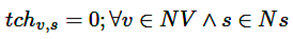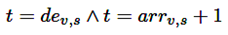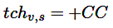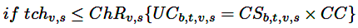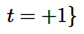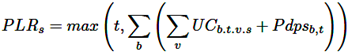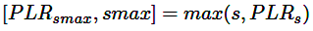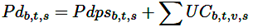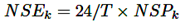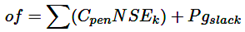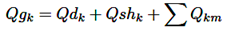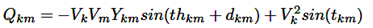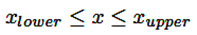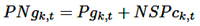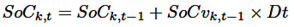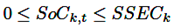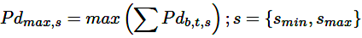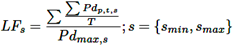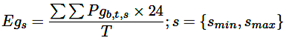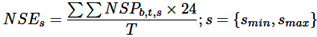Introducción
Los vehículos eléctricos (EV, electric vehicles en inglés) han ganado popularidad debido a sus bajas emisiones, alta eficiencia y costos operativos más bajos [1]. Sin embargo, el aumento en el número de EV ha significado un reto para las redes eléctricas, principalmente debido a la carga no controlada que estresa las redes de distribución (RD). Este artículo propone un sistema constituido por generación fotovoltaica (PV, photovoltaic en inglés) y almacenamiento de energía en baterías (AE) que puede ser implementado para optimizar el uso de los sistemas PV y de baterías, minimizar el costo de carga de los EV, y reducir la carga sobre la red [1, 2].
Los vehículos eléctricos representan un reto para la capacidad de la red eléctrica, la infraestructura de carga y la tecnología de almacenamiento de energía [3, 4]. El Vehicle-to-Grid (V2G) y la generación distribuida (GD) se han propuesto como tecnologías de respaldo para abordar estos aspectos [1]. Desai, et al. [5] presenta, un modelo del impacto de la adopción local de EV sobre las redes de distribución, lo cual representa un reto para los operadores de estas redes. La simulación Montecarlo (MCS, Monte Carlo simulation en inglés) puede ayudar a los operadores a entender el impacto de sus políticas sobre el desempeño del sistema e identificar los riesgos potenciales de ciertas decisiones [6] como una manera de abordar estos aspectos.
De acuerdo con el estudio de Kumar, et al. [7], la MCS es una herramienta valiosa para evaluar el impacto de factores de incertidumbre sobre el desempeño de los sistemas de potencia (SP). La condición de operación de la red de distribución de electricidad puede mejorarse usando MCS. La presencia de la variable potencia no servida (PNS) muestra condiciones de operación de déficit de potencia o sobrecarga para el SP.
Se han propuesto las tecnologías de generación fotovoltaica y de almacenamiento de energía como soluciones potenciales para integrar los EV a la red eléctrica, como se sugiere en [1], [6], al igual que la optimización de la PNS como un método para monitorear el desempeño del SP. Este método cubre los costes operacionales durante contingencias, ya que la PNS se expulsará de la carga [8]. La tecnología V2G también es una solución para los retos de la carga no controlada de EV, porque puede ayudar a mitigar los aspectos negativos y a mejorar la sostenibilidad [9]. Se ha sugerido la MCS como una potente herramienta para analizar el impacto del suministro del excedente de carga requerido por los EV utilizando GD.
De igual forma, la descripción de análisis complementario examina la interacción con el uso de EV. Wang, et al. [2] describe, la interacción entre la intermitencia producida por los generadores renovables y la capacidad de almacenamiento que se obtiene utilizando el proceso de carga V2G. Ahmadian, et al. [4] considera, una metodología estocástica asociada con el proceso de carga inteligente de EV, centrada en un análisis de la degradación de la batería. Por otra parte, Mahmud, et al. [3] se enfocan en la interacción entre las diferentes variables que se requieren para un proceso de carga inteligente. El entorno del Internet de la energía se ha adaptado de acuerdo con los futuros requerimientos de operación de una red inteligente.
Como proponen Lazarou, et al. [10], la GD puede ayudar a mitigar los impactos negativos de la carga no controlada de EV y mejorar la sostenibilidad. La GD puede suministrar energía a la red durante las horas pico para balancear la carga, reduciendo el impacto de la carga no controlada de EV sobre la red eléctrica. Es importante anticipar las deficiencias de energía para determinar las políticas energéticas apropiadas, [5] propone un modelo para caracterizar los patrones geográficos y de recorrido de los propietarios de EV para proporcionar información acerca de la conducta de viaje y demanda de energía.
El estudio propuso el uso de MCS para analizar los efectos de la carga no controlada de EV a mediano plazo. Esto contribuye a establecer políticas energéticas para satisfacer la demanda de energía de los propietarios de EV. La implementación de estas medidas mejoró la estabilidad y confiabilidad de las redes eléctricas distribuidas.
Este método proporciona un panorama de los escenarios potenciales con base en las tendencias globales y el mercado de transporte con EV en Perú, lo que resulta importante para optimizar las redes eléctricas distribuidas, utilizando modelado algebraico. El estudio apunta a asistir en el desarrollo de políticas para satisfacer la demanda energética, mientras garantiza condiciones de estabilidad y confiabilidad de la red eléctrica distribuida, [6] destaca la necesidad de estaciones de carga y de estrategias de GD debido a los requerimientos de carga de los EV.
Materiales y métodos
Se analizarán diferentes niveles de adopción de vehículos eléctricos para evaluar el impacto en la energía requerida de RD, utilizando información mundial y peruana. La proyección revisa la estratificación del parque vehicular actual e histórico del Perú.
La metodología presentada en el artículo involucra un bucle que se inicia con la información del modelo de EV y llega hasta la etapa de ahorro de data, como se ilustra en la Figura 1. Este lazo se aplica a todos los modelos de EV y los tres escenarios de adopción de Evs mencionados en la sección “2.3 Múltiples Escenarios”.
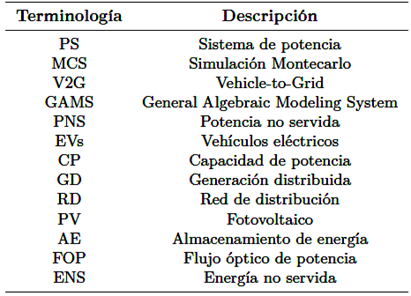
Luego, la data resultante se procesa a través de dos procesos separados. El primer proceso es la MCS, para reducir la cantidad de data. El segundo proceso es el análisis de la RD, explicado en la sección 2.6. La información recolectada en estos procesos se utiliza para comparar y evaluar el sistema diseñado que integra la generación PV y el AE para abordar el excedente de demanda de energía sobre la RD causado por la carga no controlada de EVs. La Tabla 1 muestra la terminología empleada en este artículo.

Figura 1 Metodología y data de entrada: (a) Entradas a la simulación Montecarlo acerca de modelos de vehículos eléctricos, y explicaciones de recorridos diarios. (b) Función de densidad de probabilidad (PDF) de las horas de los recorridos diarios. (c) Categoría de la velocidad de circulación diaria. (d) Función de densidad acumulativa del valor de velocidad por categoría de velocidad de circulación. (e) Resultados de la simulación Montecarlo, entrada para los próximos pasos.
Descripción de proyección de carga descontrolada en Perú
Las importaciones peruanas de vehículos eléctricos han ido en aumento (según lo informado por el Departamento de Estudios Económicos de la AAP, 2019) desde 2016. Hasta agosto de 2019, se importaron 253 vehículos híbridos y 16 eléctricos. La cantidad global de vehículos eléctricos importados anualmente fue de 11 en 2016, 93 en 2017 y 165 en 2018. En total, se informaron 535 EV hasta agosto de 2019. El Gobierno peruano informó la cantidad de vehículos en circulación hasta 2018 de cada categoría: automóviles, SUV y camionetas.
Proceso de proyección de carga descontrolada en Perú
Se proyecta las tasas de adopción de vehículos eléctricos (EV) optimistas, pesimistas y habituales en Perú. Se estima la tasa de carga controlable, utilizando la participación en el mercado como punto de referencia y calcula la tasa de carga no controlable. La tasa de carga no controlable se calcula como un complemento de la tasa de carga controlable, que se supone que varía anualmente según las tendencias regionales y globales de adopción de vehículos eléctricos.
Los supuestos para las proyecciones pesimista y optimista se basan en las tendencias actuales. Es posible que no se mantengan en el futuro. Se espera que las ventas de vehículos eléctricos continúen aumentando debido a los incentivos gubernamentales, la reducción de los costos de las baterías y una mayor concienciación de los consumidores.
Escenarios múltiples
Este estudio examina el impacto potencial del uso de EVs sobre la demanda de energía en el SP de Perú. Se presentan tres escenarios de crecimiento en su uso: bajo (15 % por año), medio (25 % por año) y alto (40 % por año). Tres escenarios de 2000, 2500 y 3750 EVs estiman el número de cargas no controladas en el mediano plazo. Los escenarios fueron establecidos utilizando datas de Perú y mundiales [11].
Sobre la base de los escenarios, los autores evaluaron el impacto potencial del uso de EV sobre el SP de Perú, bajo diferentes condiciones. Los criterios de selección para los escenarios estuvieron basados en tasas de crecimiento realistas y variadas, análisis del peor caso, y data histórica y actual. También se hace una revisión de la estratificación actual e histórica de la flota vehicular de Perú.
Hasta agosto de 2019 se importaron a Perú 253 vehículos híbridos y 16 EV. El Gobierno peruano reportó el número de vehículos de cada categoría que circularon hasta 2018 [12]. La información se encuentra detallada en la sección 2.2.
Análisis por simulación Montecarlo
La Figura 1a muestra cómo los EV salen de y llegan a diferentes barras, con horas de salida y llegada según los patrones geográficos y de recorrido de los propietarios de los EVs [5]. El modelo utiliza muestras Ns (s), T períodos de tiempo (t) y NV EV s (v), caracterizados por medio de variables estocásticas [13].
La Figura 1b muestra las variables estocásticas [9] depv,s y arrv,s a las que se le ajustan distribuciones de probabilidad [2], con variables binarias que representan los estados (depst,v,s y arrst,v,s). Las Figuras 1c y 1d muestran las caracterizaciones probabilísticas de la variable velocidad del EV (svt,v,s) y la distancia entre barras corregida usando tdcfv,s y longitud L(Frv,s: Tov,s).
(1)
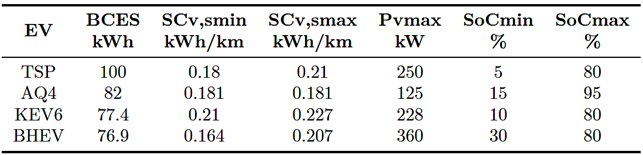
La ecuación (1) combina los parámetros estocásticos Frv,s y Tov,s del estado de la ubicación del EV con tdcfv,s, para determinar la distancia final recorrida tdv,s. Para el análisis MCS se requiere data específica del EV, como capacidad de la batería (BCES), consumo específico durante la conducción (SCv,s), estado de carga (SoCmin y SoCmax), máxima potencia de carga (Pvmax), eficiencia de carga y descarga (nchg y ndsg), valor de consumo en circulación (Rt,v,s), e índice de variable binaria (Xt,v,s).
Pseudocódigo - modelado del recorrido
Definir la hora de salida, hora de llegada, y las variables distancia temporal recorrida en circulación t = depv,s y la distancia recorrida en circulación, rdtv,s = 0 para el caso de salida, y t = arrv,s y rdtv,s = 0 para el caso de llegada.
Iniciar el bucle para llenar la distancia recorrida en circulación hasta sobrepasar la distancia recorrida, como se indica en las ecuaciones (2) y (3).
(2)
(3)
Condicional para verificar si se alcanza la última etapa del recorrido de salida, como en las ecuaciones (4) y (5).
(4)
(5)
Asignar un valor al consumo en circulación para etapas diferentes a la última en el recorrido de salida, como en la ecuación (6).
(6)
Finalizar el bucle asignando el valor de hora de finalización de la salida u hora de inicio de la llegada, y estado binario en circulación, tal como se muestra en la ecuación (7) para uno de salida y en la ecuación (8) para un recorrido de llegada.
(7)
(8)
Las variables tales como dev,s y aiv,s marcan el fin del recorrido de salida y la hora a la que el EV está listo para iniciar el recorrido de retorno, respectivamente.
La variable binaria CSb,t,v,s hace un seguimiento del estado de la barra de carga para el EV ubicado en la barra b. Las ecuaciones (9) y (10) fuerzan el cumplimiento de restricciones asociadas al estado de la barra de carga.
(9)
(10)
Las variables ChRv,s y CC se definen como la energía total requerida por el EV en circulación y la carga completa, respectivamente. Estas variables se calculan en las ecuaciones (11) y (12).
(11)
(12)
Pseudo código - modelado de la carga no controlada
(13)
(14)
Aumentar y asignar el valor de la carga no controlada del vehículo UCb,t,v,s, de acuerdo con la carga temporal tchv,s, midiendo la carga no controlada en la barra correspondiente, sin alcanzar la energía requerida, como en las ecuaciones (15) y (16).
(15)
(16)
Asignar carga no controlada al tiempo mientras se llega a la energía requerida, como en la ecuación (17).
(17)
Finalizar el bucle como en la ecuación (18).
(18)
La ecuación (19) se utiliza para obtener la información de la carga pico requerida, PLRs, que se reporta como la salida final de la MCS. La carga en la barra b del SP se representa como Pdpsb,t. La Figura 1e muestra un resumen de esta información, con el acumulado diario de la energía requerida por la RD para todos los modelos y escenarios. La Figura 1e compara las salidas máximas de la MCS que producen más carga sobre la RD durante las horas pico. Por otra parte, las salidas mínimas de la MCS representan el mínimo impacto en el estado de carga en la hora pico.
(19)
Interacción entre la MCS y el flujo óptimo de potencia
Las ecuaciones (21) y (22) muestran cómo se eligen las salidas de la MCS. El excedente de carga se agrega a la carga del SP y se denota como Pdb,t,s. La información obtenida del análisis con la MCS (ecuaciones (21) y (22)) es una entrada importante para optimizar la operación de la red eléctrica de distribución, específicamente de la subsección de transmisión, utilizando el modelado algebraico.
(20)
(21)
(22)
Flujo óptimo de potencia
El FOP eléctrica se modela en el software GAMS, utilizando la minimización de la función objetivo (fo) CONOPT de la ecuación (24) para cada uno de los seis casos (tres escenarios, dos salidas de la MCS). Este proceso suministra la cantidad de PNS requerida en cada barra de la RD para cada período analizado, como se muestra en la ecuación (25). Los enfoques de optimización GAMS y el análisis complementario con la MCS tendrían la capacidad de superar los retos de integrar EVs y GD en los SP [14].
Función objetivo
La salida principal es la energía asignada a la energía no servida (ENS) diaria, con información reportada cada media hora. Esto involucra evaluar ecuaciones para todo t ∈ T ∧ s ∈ {smin, smax}. La ENS se utiliza para asignar la cantidad de PNS durante este período de tiempo, según la ecuación (23).
La PNS se utiliza como variable auxiliar para identificar áreas y la cantidad de energía requerida para cubrir el excedente debido a la carga de EVs, y también puede representar la cantidad de potencia requerida como excedente de generación en su barra para evitar fallas del SP [8].
La función objetivo (of) para optimizar las pérdidas de energía asociadas a la operación de la red se expresa en la ecuación (24), donde también se evalúa la generación de potencia en la barra auxiliar Pgslack. Según se menciona en [15], el precio de penalización por ENS en Perú es Cpen = $6000. El uso de la PNS como fuente de datos puede ayudar a los planificadores a comparar las fuentes alternativas de generación, ajustar la energía requerida en el modelado especio-tiempo, y dimensionar las condiciones de GD en el SP.
(23)
(24)
Restricciones para el flujo óptimo de potencia
Las restricciones para el FOP son el balance de potencia activa y reactiva. Las ecuaciones (25) y (26) definen el balance de potencia, donde Pgk y NsPk denotan la potencia de generación y las reservas no rotativas, mientras que Pdk representa la potencia requerida por la carga.
(25)
(26)
Las variables Qgk, Qdk están relacionadas con la potencia reactiva de generación y carga en cada barra. Las ecuaciones (27) y (28) calculan la potencia activa y reactiva por línea (Pkm y Qkm) y la potencia aparente Skm en la ecuación (29) controla la sobrecarga en la línea de potencia correspondiente.
(27)
(28)
(29)
Las variables Vi, di, Qgi, Pgi tienen límites inferior y superior, denotados por xlower y xupper en la ecuación (30). La sección se refiere a [8] para los detalles sobre los parámetros de voltaje (V y d) y los parámetros de la matriz de admitancia (Y y t).
(30)
Capacidad del nuevo sistema de potencia para garantizar operación normal
Se consideraron dos opciones para el modelo desarrollado para determinar el momento y la barra de falla. La primera opción involucra un incremento lineal de la capacidad de potencia (CP) en una barra específica. La segunda opción es una combinación de generación PV y un sistema de AE.
La ecuación (31) describe la primera opción, la cual modela la nueva CP (PNgk,t) para operar durante el día y recuperar los costos de inversión. La segunda opción apunta a minimizar la función objetivo de costos adicionales, con costos agregados xcost de acuerdo con la PNS calculada (NSPck,t).
(31)
Las ecuaciones (32), (33) y (34) describen el proceso de la segunda opción, la cual cubre la nueva CP requerida, incluyendo la dimensión de la potencia (PhPCb) y el almacenamiento de energía (SSECb), y se ajusta según la variación de la disponibilidad solar (Saft) y del estado de carga (SoCvk,t) para redistribuir la energía almacenada cada media hora (Dt). La fuente de la capacidad de generación excedente no se analiza debido a su variedad.
(32)
(33)
(34)
Impacto sobre la red de distribución
Los estudios indican que los vehículos eléctricos tienen un impacto sobre las redes de distribución. Los requerimientos diarios de energía son independientes del modelo de EV. La data de voltaje y la energía requerida por los EV se recopila y se procesa mediante ciencia de datos, obteniendo información estadística utilizando MCS. La carga de los EV puede causar caídas de voltaje e inestabilidad en la red, lo cual puede ser abordado usando sistemas de almacenamiento de energía y estrategias inteligentes de carga [2], [5].
Caso de estudio
Carga no controlada de vehículos eléctricos (datos proyectados 2023-2031)
Las suposiciones y las fuentes de información utilizan la participación de mercado como un punto de referencia para las tasas regionales y globales de carga controlada. Las ventas acumuladas de EV se consideran como el total de EV en circulación, y se espera que las ventas de los mismos continúen incrementándose debido a incentivos gubernamentales, costos reducidos de baterías y aumento en la conciencia del consumidor.
La proyección optimista supone un aumento anual de 25 % en las ventas de EV, y supone que la tasa de carga controlada es 70 %. La proyección pesimista supone un aumento anual de 10 % en las ventas de EV, y supone que la tasa de carga controlada es 50 %. Estas suposiciones se utilizaron para proyectar la adopción de EV en Perú.
La Tabla 2 presenta los rangos de la proyección de la adopción de EV en Perú entre 2023 y 2031. Esto incluye las ventas acumuladas, las tasas de carga controlada y no controlada, y el número de EV en circulación. La data se presenta en los escenarios optimista, pesimista y normal.
Múltiples escenarios
El artículo presenta tres escenarios para el crecimiento de la venta de EV en Perú: optimista, normal y pesimista, con estimaciones de tasas de carga controladas para cada escenario. Basándose en esta información y al análisis de la carga no controlada de los EV, el estudio proyecta que el número de EV circulando en Perú para 2023 variará entre 2450 y 2940. El artículo también compara las características técnicas de diferentes modelos de EV y sus efectos sobre la RD, como se muestra en la Tabla 3; se encontró que el KIA EV6 es el vehículo que requiere más energía entre los EV estudiados. Sin embargo, los escenarios presentados se basan en suposiciones generales, y puede que no reflejen de manera precisa las condiciones específicas del mercado peruano. Ver la Tabla 2 para mayor información.
Análisis por simulación Montecarlo
El estudio analizó tres escenarios con microescenarios estocásticos. El escenario 1 consistió en 2000 EV con 200 muestras. El escenario 2 tuvo 2500 EV con 120 muestras. El escenario 3 tuvo 3750 EV con 80 muestras. El análisis incluyó 1.0 × 10+6 escenarios microestocásticos con incertidumbre. En la sección 2.2 se ajustó una distribución normal a las variables depv,s y arrv,s. La Figura 1b ilustra las diferencias significativas entre las funciones de distribución de probabilidad de las horas de salida y llegada. Las horas de llegada tienen una desviación estándar que engloba horas después del trabajo cuando los individuos pueden atender tareas el hogar o socializar, lo cual no ocurre durante las horas de la mañana antes del trabajo.
De acuerdo con [13], el Tesla Model 3 tiene una BCES de 2.88 × 10+8 J (80 kWh). El consumo específico de energía para este vehículo está dentro del rango de SCv,s ∈< 684; 900 > J/m(< 0.19; 0.25 >KWh/Km). La máxima potencia de carga del EV es aproximadamente Pvmax = 1.5 × 10+5 W with nchg = 90 % y ndsg = 90 %. Para modelar las baterías del EV, se establece el estado de carga mínimo SoCmin en 15 % de la capacidad de la batería, mientras que el estado de carga máximo SoCmax se establece en 95 % de la capacidad de la batería.
Interacción entre la MCS y el FOP
La caracterización de la incertidumbre del recorrido y geográfica involucra categorizar el número de EV por barra como “desde” o “hacia” según el recorrido de salida. La Figura 2 muestra diagramas de caja de la energía total requerida por la RD en cada hora, comparando el KIA EV6, que requiere la mayor cantidad
de energía, con el Tesla Model 3, que requiere la menor cantidad de energía (como se muestra en la Figura 1e). Los valores reportados en la Figura 2 muestran que el KIA EV6 es el modelo que consume más energía, provocando un mayor requerimiento de energía para la RD.
Uso del flujo óptimo de potencia
El sistema de potencia IEEE de 14 barras [16] representa el SP de la clase socioeconómica A en Perú, con variaciones en la longitud de la línea de potencia. La data de carga del mercado eléctrico de febrero de 2020 se utiliza como el factor de carga diario. Los efectos de las categorías de circulación de alta, media y baja velocidad se reportan en [13]. Google Maps suministró data histórica de tráfico para las tres categorías representadas por distribuciones normales. La primera categoría es velocidad alta con un valor promedio de 13.89 m/s (50 km/h) y una desviación estándar de 5.56 m/s (20 km/h). La segunda categoría es velocidad media, con un valor promedio de 9.72 m/s (35 km/h) y una desviación estándar de 4.17 m/s (15 km/h). La tercera categoría es velocidad baja, con un valor promedio de 5.56 m/s (20 km/h) y una desviación estándar de 2.78 m/s (10 km/h).
Capacidad del nuevo sistema de potencia para garantizar operación normal
La opción del primer CP excedente no necesita data adicional, pero la opción del sistema con generación PV y almacenamiento de energía requiere un factor de disponibilidad solar, obtenido de [17] con data de costos de [18]. La subsección 2.5 presenta las restricciones y la función de la interacción de potencia con PNS. Las restricciones (32) a (34) son complementadas por la ecuación (35), manteniendo la variable SoCk,t entre los límites de 0 y la capacidad del sistema de almacenamiento, SSECk.
(35)
Las variables de la función objetivo en la ecuación (33) incluyen un PhPCcost de 1.30 $/W para el costo de CP fotovoltaica y un SSECcost de 1.11 × 10−4 $/J (400 $/kWh) para la capacidad del sistema de almacenamiento de energía.
Análisis de la red de distribución
Finalmente, se obtienen dos síntesis muy similares a la data global. La primera representó el 4 % de los casos, y la otra correspondió al 10 % de los casos. Estas reducciones son evaluadas en una red de distribución comúnmente utilizada (el sistema IEEE de 14 barras) mediante la herramienta Simulink del software MATLAB. El efecto de todas las simulaciones realizadas en la RD se reporta en la siguiente sección.
Resultados y discusión
Análisis por simulación Montecarlo
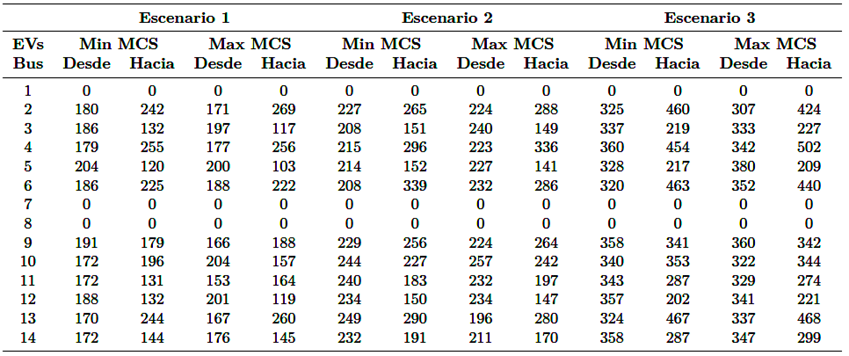
La Figura 3 muestra el número de EV en el SP y dos figuras para cada escenario, ilustrando los patrones geográfico y de recorrido de los EV. La Tabla 4 proporciona información adicional sobre el número de EV saliendo de y llegando a cada barra en su primer recorrido, junto con la incertidumbre de los patrones geográficos. Los encabezados en la Tabla 4 están clasificados como “Min MCS” y “Max MCS”, representando los escenarios mínimos y máximos de carga pico diaria reportados en las salidas de la MCS. Estos clasificadores pueden ayudar a evaluar los potenciales impactos de los EV sobre el SP.
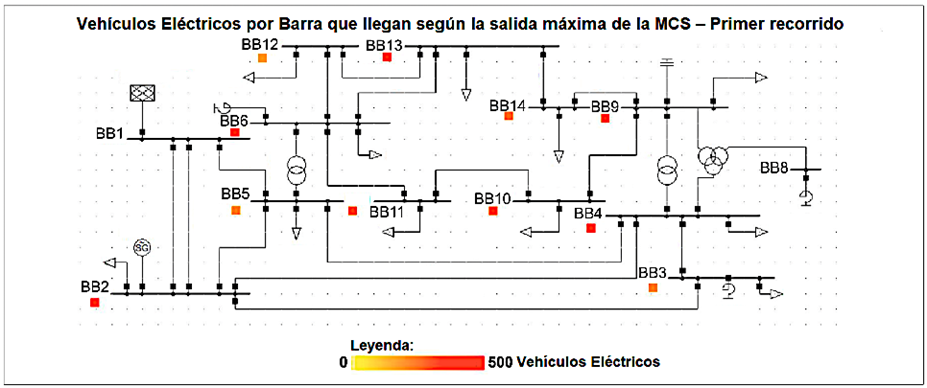
Figura 3 Número de vehículos eléctricos que llegan según la salida máxima de la simulación Montecarlo - escenario 1
Interacción entre la MCS y el FOP
La Figura 4 compara la aplicación para el Tesla Model 3, que tiene el consumo específico más bajo. La primera aplicación es el PSMCS, que se muestra en la sección derecha. Los valores también están relacionados con la salida máxima de la MCS. Mientras tanto, la Tabla 5 presenta las características promedio de carga diaria para diferentes escenarios con salidas mínimas y máximas de la MCS.
La energía de la carga Eds se calcula mediante la ecuación (36). La carga pico Pdmax,s representa la carga máxima diaria suministrada por el SP para cada escenario analizado, como se expresa en la ecuación (37).
Finalmente, el factor de carga LFs se determina dividiendo la potencia promedio de la carga por la potencia máxima de la carga, como se muestra en la ecuación (38).

Figura 4 Comparación del desempeño del sistema de potencia: flujo óptimo de potencia (PS_MCS), fotovoltaico y almacenamiento de energía (NPS_PVES) y generación continua (NPS_Cont)
Tabla 5 Data de carga por escenario para el vehículo eléctrico Tesla (2018) y desempeño del flujo óptimo de potencia para todos los escenarios

(36)
(37)
(38)
Se observa un incremento en la diferencia en la carga pico entre las salidas máximas y mínimas de la MCS, lo cual indica el efecto estocástico del análisis. Para el escenario 1, la brecha entre las salidas de la MCS es 2.41×10+6 W. Para el escenario 2, la diferencia entre las salidas de la MCS es 2.60×10+6 W. Para el escenario 3, la brecha entre las salidas de la MCS es 6.72 × 10+6 W. A continuación, se reporta la diferencia en la energía diaria de la carga entre las salidas máximas y mínimas de la MCS para cada escenario. El escenario 1 tiene una diferencia en la energía diaria de 5.13 × 10+10 J (14.24 MWh). El escenario 2 tiene una diferencia en la energía diaria de 6.45 × 10+10 J (17.92 MWh). El escenario 3 tiene una diferencia en la energía diaria de 9.66 × 10+10 J (26.84 MWh). El incremento en la brecha se debe al número de EV en los escenarios evaluados.
Uso del flujo óptimo de potencia
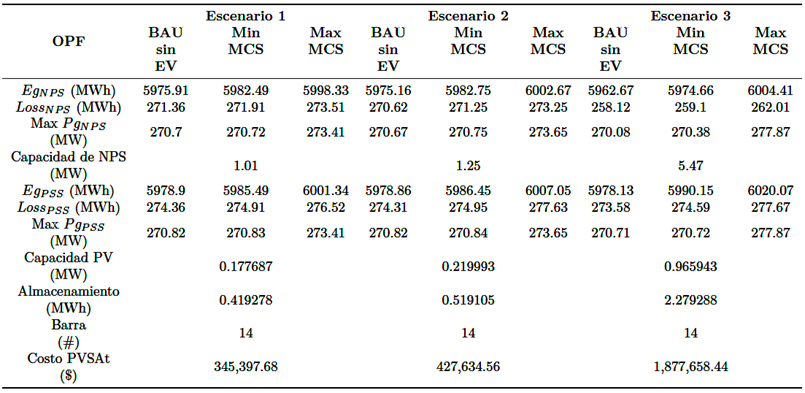
Comúnmente, el modelo emplea el FOP para evaluar el desempeño del SP para los diferentes escenarios de carga de EV. La Figura 4 muestra el desempeño de la CP y la PNS requerida para mantener la operación normal, donde se especifica la salida más alta de la MCS para el EV Tesla 3 Model. La Tabla 5 resume los hallazgos del flujo óptimo de potencia, incluyendo variables tales como Egs y Losss, que representan energía generada, brechas de energía y NSEs asignando PNS a todas las barras durante el día. Las ecuaciones (39) a (41) definen estas variables.
(39)
(40)
(41)
El modelo evaluado permite identificar la barra que requiere mayor capacidad y cuál es la opción más apropiada para suministrarla. La cantidad de PNS determinará la capacidad requerida para nuevas plantas eléctricas. La Tabla 6 reporta información para el Tesla 3 Model (2018).
El estudio encontró que se expulsó ENS de la última barra del SP, que es la que está más alejada de las barras de generación (#14). La cantidad de ENS se incrementó a medida que aumentó el número de EV en cada escenario.
Capacidad del nuevo sistema de potencia para garantizar operación normal
El SP requiere capacidad adicional de generación para abordar el problema identificado. La sección de metodología ofrece opciones para obtener capacidad extra de generación usando microturbinas, máquinas de combustión interna, generación PV en conjunto con un sistema de almacenamiento, etc. La Figura 4 muestra el desempeño del SP y la potencia suministrada por el sistema PV-AE para la salida máxima de la MCS para el Tesla 3 Model. La Tabla 5 proporciona información acerca de la capacidad requerida del nuevo sistema de potencia (NSP). El costo del sistema PV-AE se reporta para cada escenario en las Figuras 5a, 5b, y 5c, variando desde $ 0 a $7.40 ×10+5 para el escenario 1, $ 2.22 ×10+5 a $ 7.81 ×10+5 para el escenario 2 y $ 5.88 ×10+5 to $3.41 ×10+6 para el escenario 3. El costo de la primera opción para agregar capacidad para un día completo no se evalúa en este estudio, pero su CP se establece como constante, tal como la PNS del SP FOP.
Resultados de la red de distribución
La sección 3.4 del estudio examina la relación entre carga y capacidad del SP. Se encontró que un aumento en la carga general no necesariamente requiere mayor capacidad del SP o incrementa el costo de generación PV y AE. Este estudio también muestra que la carga requerida por los modelos de EV no resulta en mayor PNS. Estos hallazgos sugieren que los requerimientos del SP y del modelo de EV son independientes.
Se utilizan técnicas de reducción de datos para sintetizar la gran cantidad de información procesada. Se realizaron dos reducciones en los datos, con errores de 1.24 % y 0.85 % en comparación con la data global. La reducción de 4 % de la data se utiliza para procesar la data en MATLAB mediante la herramienta Simulink. La data de la red de distribución se utiliza para redistribuir los EV entre los alimentadores del sistema de potencia IEEE de 14 barras, y el desempeño resultante de los alimentadores se muestra en la Figura 6. Los resultados indican que los valores de voltaje permanecen dentro del rango para todas las barras del sistema de potencia IEEE de 14 barras, aún bajo suposiciones de carga no controlada.
Conclusiones
En este estudio se muestra el efecto de la presencia de carga no controlada de EV en los mercados eléctricos, como puede verse en la Tabla 5 y en la Figura 2. Las salidas mínimas y máximas de las simulaciones Montecarlo dependen del consumo específico de los modelos de EV, cuyos valores se reportan en la Tabla 3. El modelo de EV que requirió más energía de la red de distribución fue el KIA EV6, mientras que el modelo que
requirió menos energía fue el Tesla Model 3, como se muestra en la Figura 1e. El mayor consumo del escenario 3 fue para el modelo KIA EV6, con 31.8 MWh, mientras que el menor consumo del escenario 1 fue para el Tesla Model 3, con 10.14 MWh.
Para los modelos específicos de EVs que requieren más energía, no se garantiza que la variable PNS sea necesaria. La Figura 5a muestra que los modelos que no tuvieron PNS fueron el KIA EV6 (que tiene el mayor requerimiento de energía) y el Tesla S Plaid. Las Figuras 5b y 5c también soportan este hecho debido a la intermitencia de las PNS máximas y mínimas que se presentan en las ejecuciones de FOP.
Por otra parte, la dependencia que se observa en la Figura 5 es la relación entre los costos de sistemas de generación PV - almacenamiento de energía de diferentes dimensiones y la cantidad de ENS diaria presente en la ejecución del FOP. Esta relación no es estrictamente lineal, pero para valores similares de ENS
el costo del sistema diseñado es similar. Por ejemplo, en el escenario 3, el valor más alto de ENS es 6.84 MWh. El modelo de EV correspondiente es el KIA EV6. El costo relacionado con este punto es $ 2.84 ×10+6. Sin embargo, el costo más alto entre los sistemas diseñados es $ 3.41 ×10+6, con un valor de energía no servida de 5.94 MWh.
El impacto de la carga no controlada no es relevante en la distribución, como lo muestra la estabilidad de voltaje en el modelo ejecutado. Aún las barras más alejadas tienen valores de voltaje que cumplen con los límites de las normas peruanas de distribución eléctrica. Las barras 632, 645, 646 y 633 tienen niveles de voltaje bien distribuidos. Los restantes también tienen valores de acuerdo con las normas.