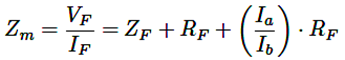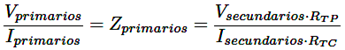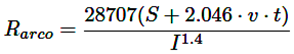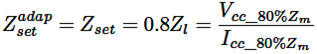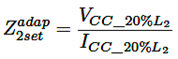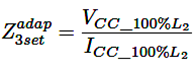Introducción
El ingreso de las ERNC puede poner en peligro la coordinación del alcance de las zonas de protección de los relés de distancia [1], principalmente debido a la naturaleza estocástica de sus recursos [2]. Por lo tanto, es necesario considerar una modificación, análisis y rediseño de las protecciones para que puedan adaptarse a la variación de la corriente de falla provocada por las energías renovables [3].
El relé de distancia calcula la impedancia aparente al punto de falla mediante las mediciones de tensión y corriente, y compara este valor con la impedancia de ajuste para determinar la zona de actuación. La diferencia entre las centrales convencionales y las fuentes basadas en inversores radica en la contribución de corriente en un escenario de falla. Normalmente, una central convencional aporta entre 5 a 6 veces la corriente nominal, a diferencia de las fuentes renovables cuya corriente de falla se encuentra entre 1.1 a 2 veces [3], y por ende las componentes de secuencia son distintas entre estos dos tipos de fuentes. Debido a esta diferencia, varios autores han planteado posibles soluciones para evitar el problema de subalcance y sobrealcance de la protección de distancia.
Otro punto que se debe considerar al calcular un escenario de cortocircuito es la resistencia de falla, la cual puede ocasionar problemas de subalcance en los relés de distancia. Para mejorar el funcionamiento de la protección ante esta situación, se propone el uso de nuevos algoritmos de estimación de la impedancia de la línea que integran la resistencia de falla en fuentes de generación síncrona [4]. Además, [5] utiliza la característica de tipo MHO para ajustar la zona de protección y resolver los problemas de operación del relé en plantas fotovoltaicas.
Por otro lado, [6] propone una metodología de ajuste utilizando la característica cuadrilateral, teniendo como resultado el cambio del límite de actuación del relé durante la variación de la impedancia medida, debido a la inserción de la resistencia de falla.
En este artículo se presenta una metodología de protección de distancia de la característica cuadrilateral para proteger las líneas de transmisión conectadas a fuentes de energía renovales no convencionales, como parques eólicos, con la finalidad de mejorar el ajuste de las zonas de operación del relé cuando el sistema enfrenta fallas de fase con resistencias de falla, las cuales pueden hacer que la impedancia aparente calculada por el equipo sea notablemente mayor.
Las contribuciones de este artículo incluyen:
Modelamiento detallado de la ERNC para verificar las aportaciones de corriente de falla vistas por el relé de protección.
Desarrollo de un método de ajuste basado en el cálculo de corrientes de cortocircuito de fase al 80 % y 20 % de la longitud de las líneas principal y adyacente. Esta expresión matemática permite la variación independiente de la resistencia y reactancia en el plano R-X, lo cual resuelve el problema de subalcance del relé al tener en cuenta la resistencia de falla.
El funcionamiento de la metodología propuesta ha sido constatado mediante datos de simulación para diferentes tipos de falla y a generación variable del parque eólico.
El resto de este documento se organiza como sigue. En la sección 2 se presenta los conceptos básicos de la protección de distancia con característica cuadrilateral ante la integración de ERNC, se brinda una breve descripción del esquema eléctrico a estudiar y los efectos de la resistencia de falla dentro de un evento de cortocircuito. En la sección 3 se detalla la metodología propuesta, y los resultados que evalúan su desempeño en diferentes situaciones se presentan en la sección 3.2. La discusión sobre la metodología planteada se fundamenta en la sección 3.3 y, finalmente, las conclusiones del trabajo se exponen en la sección 4.
Materiales y métodos
Protecciones eléctricas de un sistema de potencia ante la inserción de las ERNC
Las fallas en un sistema de potencia pueden provocar daños en los elementos, por eso es indispensable minimizar su efecto a través de un sistema de protecciones que lo vuelven más confiable y seguro [7]. La línea de transmisión, al ser el elemento más vulnerable del sistema, cuenta con una protección primaria (relé de distancia). En esta sección, se dará a conocer su principio de operación y sus características [8].
Descripción del sistema
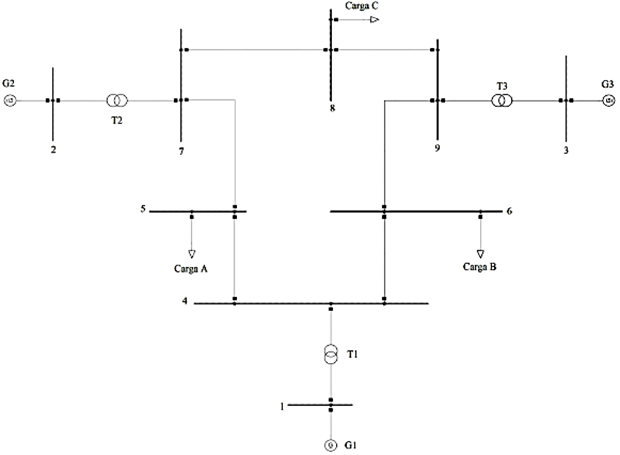
Para el caso de estudio, se ha considerado el sistema New England de 9 barras IEEE [9] de 230 kV a 60 Hz, como se muestra en la Figura 1. Se procede a dividir el sistema en dos sectores: el 1 está compuesto por las barras de color gris, mientras que el 2 se compone de los elementos de color negro.
Red equivalente del sistema modificado
El sector 1 será reemplazado por un circuito equivalente calculado mediante el método de REI, que se deriva de “radial”, “equivalente” e “independiente” [10]. El cual separa el sistema en sectores activos y pasivos con el objetivo de agrupar los sectores pasivos en una barra común o equivalente, la misma que contiene los valores de corriente y potencia de cortocircuito trifásico y monofásico en la barra común, así como también la constante de inercia de los generadores del sistema.
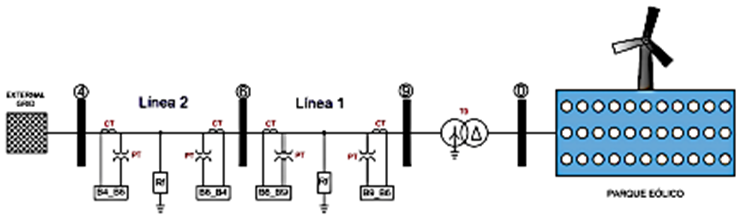
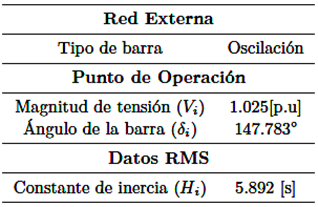
Los parámetros característicos de la red equivalente conectada al sistema mostrado en la Figura 2 son detallados en la Tabla 1.
Para el cambio de la estructura del sistema se considera la inserción de una nueva barra (0), donde se integra el parque eólico, el cual tiene 11 circuitos cada uno con tres aerogeneradores de 2.5 MW conectados en paralelo, dando una capacidad instalada del parque de 82.5 MW.
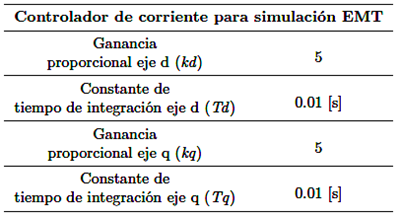
Los aerogenadores utilizados son propios de la librería de Digsilent Power Factory®; el generador está acoplado a la red a través de un convertidor de tensión (VSC) con una tecnología full-converter [11] los datos de entrada de estos controladores se detallan en la Tabla 2.
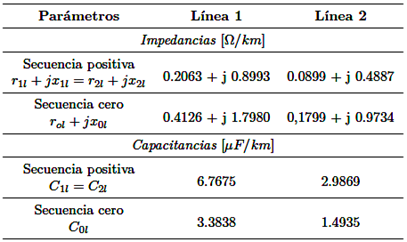
Para el análisis posterior, la longitud de las líneas 1 y 2 son de 100 km, sus parámetros eléctricos son descritos en la Tabla 3:
El transformador tiene una potencia nominal de 150 MVA, 230/13.8 kV, conexión YnD5, el lado de baja adelanta 150° al lado de alta y la reactancia de cortocircuito es de 8.79 %.
Característica cuadrilateral del relé de distancia
Dentro de la protección de distancia, la característica cuadrilateral es más versátil, ya que no presenta una reducción en su zona de protección efectiva cuando existe resistencia de falla, mientras la impedancia medida se encuentre dentro del cuadrilátero, el relé funcionará correctamente [12].
Principio básico
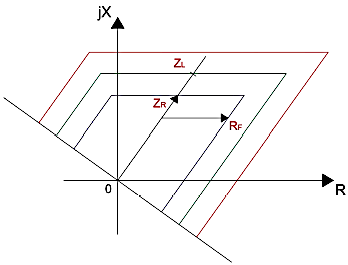
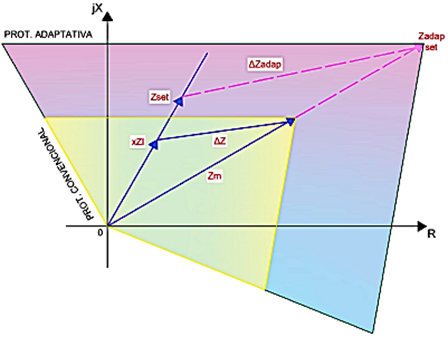
La ventaja de este tipo de relé, es que la zona de operación depende solamente de la impedancia del elemento a proteger, lo cual prácticamente se mantiene constante, es decir, no depende de las magnitudes tanto de corriente como de voltaje [13]. La característica cuadrilateral es uno de los métodos más utilizados. Los ejes horizontales de esta protección dependen solo del valor de reactancia “X”, mientras que los ejes verticales pueden ser modificados al variar la resistencia “R”. Esto se representa en el plano R-X (Figura 3), lo cual resulta en un mayor alcance de protección al momento de la inserción de la resistencia de falla [14].
La característica cuadrilateral opera si la impedancia medida por el relé se encuentra dentro de la reactancia de carácter positivo y negativo de los lados derecho e izquierdo, descritos en la figura anterior.
Donde:
Zonas de protección del relé
La protección de una línea de transmisión no se puede dar por una única zona, puesto que los transformadores de instrumento deben ser muy precisos, se requiere protecciones de respaldo [1].
El porcentaje asignado a cada zona a proteger se analiza de acuerdo con la característica del relé. En el caso de la característica cuadrilateral, las asignaciones operan de la siguiente manera:
La zona 1 está configurada para proteger entre el 80 % y el 90 % de la línea donde se produce la falla. El tiempo de actuación del relé es inmediato, t1 = 0 segundos, ya que la protección de distancia debe activarse antes que cualquier otra protección.
Por otro lado, la zona 2 abarca toda la línea donde ocurrió la falla, junto con el 20 % de la línea adyacente. El tiempo de activación del relé es de t2 = 0.4 segundos.
La zona 3 cuenta con un intervalo de tiempo de coordinación de t3 = 0.8 segundos y es capaz de proteger completamente la línea donde ocurrió la falla, así como el 100 % de la línea adyacente [15].
Efectos de la resistencia de falla
La impedancia de una línea de transmisión se distribuye uniformemente a lo largo de su longitud. Esta característica da posibilidad al relé de distancia para identificar entre fallas interiores y exteriores, las cuales podrían variar por la resistencia de falla. Esta resistencia puede surgir por fallas en los aisladores o por la inducción de rayos, y cuando ocurre, genera un arco eléctrico que debe tenerse en cuenta al ajustar el funcionamiento del relé [16].
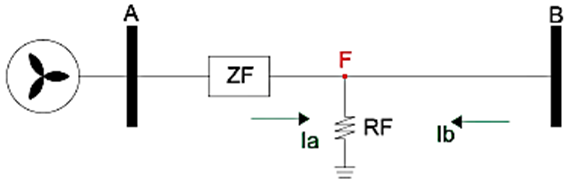
De acuerdo con el diagrama mostrado en la Figura 4, la impedancia vista por el relé con la inserción de la resistencia de falla del sistema se da por medio de la ecuación (1)
(1)
Donde:
Zm = Impedancia medida en las barras A y B
ZF = Impedancia de falla
RF = Resistencia de falla
Ia = Corriente medida barra A
Ib = Corriente medida barra B
En la Figura 3 se puede observar que, en la característica cuadrilateral, la resistencia de falla se encuentra cercana al límite de disparo del relé, esto provoca que la falla sea percibida más lejos de su ubicación real, lo que resulta en un alcance de protección más limitado y tiempos de actuación erróneos, por esta razón es necesario modificar el ajuste típico del relé y utilizar un enfoque adaptativo [13] [16].
Criterios para el ajuste de relé de distancia
Tanto el voltaje como la corriente tomada por los transformadores de potencial (TP) y corriente (TC), son los que estiman la impedancia del relé, la misma que se expresa por Ωprimarios, al usar la conversión por la relación entre el TP⁄TC, la lectura que toma el equipo se da por Ωsecundarios, para convertir la impedancia primaria en secundaria se usa la expresión [17], ecuación (2):
(2)
Para los relés comerciales SIEMENS 7SA522 [17], los ajustes de la protección generalmente tienen la siguiente forma,(tabla 4):
La característica cuadrilateral presenta una particularidad importante: el ajuste del alcance reactivo y resistivo es independiente. Esta particularidad es útil cuando se tiene una resistencia de falla dentro del sistema, ya que esto es un parámetro que dificulta la correcta medición del relé de distancia [15]. Al producirse una resistencia de falla genera un arco el cual presenta una resistencia eléctrica, la que puede ser calculada mediante la fórmula de Warrington, presentada en la ecuación (3) [18].
(3)
Donde:
S = Distancia de aislamiento fase-fase [m]
I = Corriente de cortocircuito [A]
v = Velocidad del viento [m/s]
t = Tiempo de duración del cortocircuito [s]
La adición de la resistencia de arco no modifica los valores de la impedancia de la línea, por lo que la protección sigue midiendo la reactancia directa de la línea, pero la resistencia vista por el relé, si considera esta resistencia de arco [17], como se explica en la Tabla 5.
Resultados y discusión
Aplicación al caso de estudio
En este apartado se realiza una comparación entre los sistemas de protección de un generador síncrono y un generador eólico con características operativas similares. El objetivo es validar su correcto funcionamiento en los escenarios planteados.
Cálculo de cortocircuito
Para este análisis se realiza el cálculo de cortocircuito por medio del método completo o de superposición, el cual evalúa la corriente de falla en un punto específico de la red, su principal objetivo es verificar si la falla del sistema de protección depende del comportamiento erróneo del relé o de sus ajustes incorrectos. Para dimensionar adecuadamente el equipo de protecciones es necesario conocer dos corrientes de cortocircuito, la máxima dada por una falla trifásica (al principio de la línea) que determina el límite de disparo de los relés y la mínima por una falla fase-neutro (al final de la línea) que sirve para elegir la curva disparo del relé [19].
Corriente de falla
Los sistemas eléctricos alimentados por generadores síncronos por su topología producen fallas trifásicas, bifásicas y monofásicas, lo que afecta al flujo normal de la corriente en las líneas de transmisión. Mientras que los sistemas con fuentes de ERNC (eólica), por su estructura basada en electrónica de potencia, carecen de conexiones a tierra, por tal motivo no posee secuencia cero.
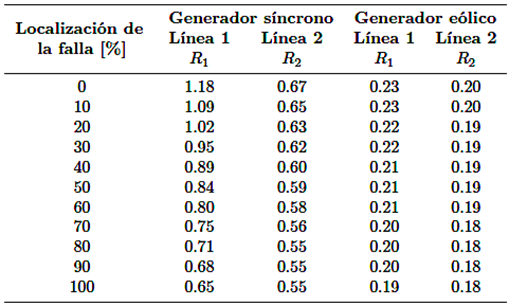
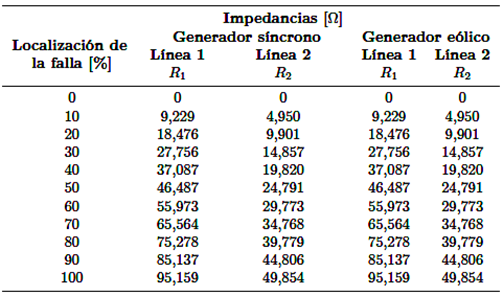
Para proteger el sistema de control del generador eólico, la corriente de falla se encuentra en el rango de 1.1 a 1.5 veces su corriente nominal, en tanto en el generador síncrono el aporte es de 5 a 6 veces la corriente nominal. Esto se puede demostrar en la Tabla 6 , que contienen los resultados de la corriente al producirse fallas en diferentes puntos de la línea, cuando el sistema está conectado al generador síncrono y a un parque eólico, evidenciando la premisa que, la corriente de falla es menor en un sistema de generación renovable [20]. El relé R1 se encuentra conectado a la barra 9 que protege a la línea 1, mientras que el relé R2 protege a la línea 2 y está instalado en la barra 6 del sistema.
Impedancias de falla
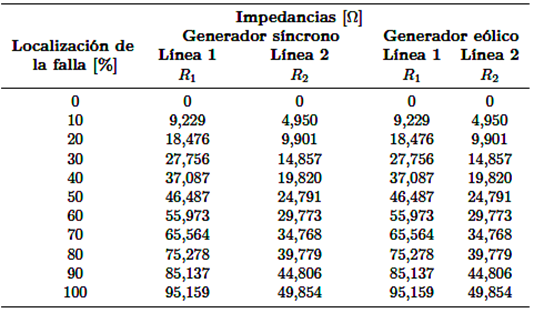
El principio básico de la protección de distancia es medir la impedancia aparente a partir de la relación de corriente y voltaje (V/I). De acuerdo con esta relación, al producirse una falla, si la corriente de cortocircuito aumenta en compensación la caída de voltaje disminuye. Por esta razón, la impedancia se ve afectada ligeramente al variar el nivel de cortocircuito, el tipo de falla o la fuente de alimentación del sistema, demostrando que la impedancia tendrá cambios significativos si la falla presenta una resistencia de falla [21]. Según lo expresado en el párrafo anterior, en la Tabla 7 y 8 se puede demostrar que la impedancia para una falla trifásica y bifásica en una línea de transmisión alimentada por un generador eólico o síncrono es la misma siempre y cuando la resistencia de falla sea igual a cero.
Fluctuación de la generación
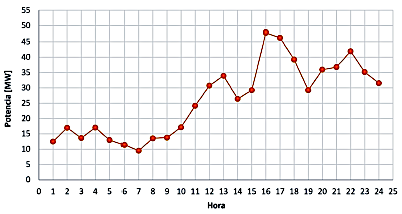
Un parque eólico consta de varias unidades conectadas en paralelo, a lo largo del día no todas las unidades pueden estar operativas debido al mantenimiento o la variabilidad de las condiciones climáticas, lo que resulta en una variación en la potencia de salida, es decir, la línea transportará potencia variable. Estos cambios podrían representar un mal funcionamiento del relé de distancia ante una falla [22]. En la Figura 5 se observa la potencia activa generada por el parque eólico a lo largo del día, destacando dos momentos, a las 16:00 horas la potencia del parque alcanza su máxima generación diaria de 47.91 MW y a las 7:00 horas la generación es mínima con 9.53 MW.
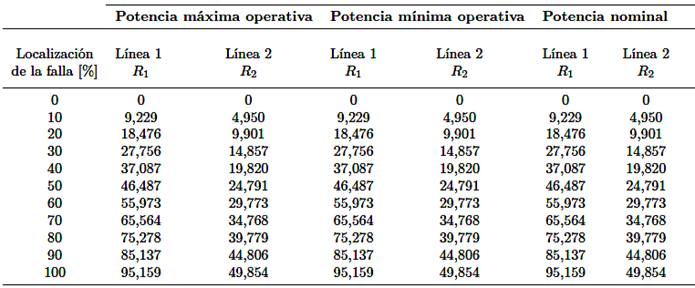
Al calcular el cortocircuito en la línea, variando la localización de la falla y la generación del parque eólico, se evalúan las impedancias de falla a potencia instalada (82.50 MW), máxima operativa (47.91 MW), mínima operativa (9.53 MW), nuevamente se evidencia que la impedancia vista por el relé es la misma en los tres escenarios de operación y con resistencia de falla cero. (Tabla 9)
Método de ajuste adaptativo
En la sección 2 se explica la influencia de la resistencia de falla durante el cálculo de cortocircuito en una línea de transmisión, un subalcance en la protección podría provocar disparos erróneos del relé, por ello el ajuste típico del equipo debe ser modificado por uno adaptativo.
El método de ajuste adaptativo cuadrilateral permite la variación individual de la resistencia y reactancia en el plano R-X, provocando un incremento en las zonas de protección. Esto ayuda al sistema a tener mayor flexibilidad y precisión al momento de la inserción de la resistencia de falla.
La característica del relé cuadrilateral adaptativa ajustada para la zona 1 se puede representar de la siguiente manera: ecuación (4).
(4)
Donde Zset es la impedancia de ajuste convencional del relé, la cual representa un cortocircuito al 80 % de la línea 1, ubicada en la barra 9-6 (Figura 2). Al momento de referirnos a las zonas de protección 2 y 3, se deberá analizar la línea adyacente ubicada en las barras 6-4.
Cuando ocurre una falla y la resistencia de falla es igual a cero, la impedancia Zm = xZL1 , donde x representa el porcentaje de localización de la falla. Sin embargo, cuando la resistencia de falla es diferente de cero, ocasiona un cambio en ΔZ, provocando un error en la impedancia medida Zm y en la impedancia de falla xZL1 .
Para evitar mediciones erróneas del relé, en la Figura 6 por medio del plano R-X, se representa el incremento de la impedancia medida Zm; a la nueva impedancia se la determina por Z set adap . Este es el nuevo ajuste de protección al momento de producirse una falla.
Para implementar el método adaptativo en la zona 2 se calcula un cortocircuito al 20 % de la línea adyacente (L2) y para la zona 3 un cortocircuito al 100 % de L2. El ajuste adaptativo del relé se describe a continuación:
Zona 2: equación (5).
(5)
Zona 3: equación (6).
(6)
Donde:
Zadap = Impedancia adaptativa
Vcc−80% = Tensión de cortocircuito al 80 % de L1
Icc−80% = Corriente de cortocircuito al 80 % de L1
Vcc−20% = Tensión de cortocircuito al 20 % de L2
Icc−20% = Corriente de cortocircuito al 20 % de L1
Vcc−100% = Tensión de cortocircuito al 100 % de L2
Icc−100% = Corriente de cortocircuito al 100 % de L1
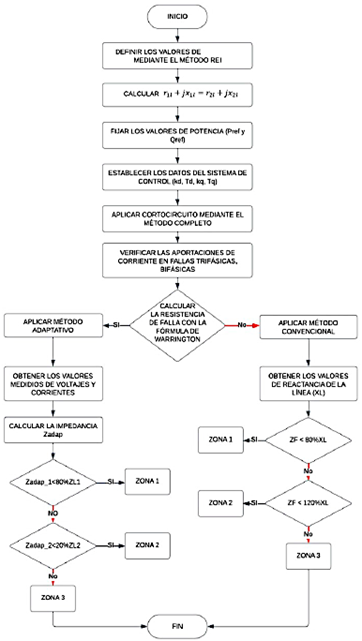
Diagrama de flujo
La Figura 7 muestra el diagrama de flujo del método propuesto. Para la aplicación de este, al sistema base se debe aplicar un modelo equivalente mediante el método de REI. Luego se establecen los parámetros de secuencia positiva, negativa y cero de las líneas de transmisión, seguido de esto se ingresa los valoresde potencia antes de la falla, al conectar el parque eólico considerar los datos de entrada del controlador. Finalmente, se calcula un cortocircuito trifásico con resistencia de falla de 0 y 25 WΩ Cuando el valor de resistencia de falla es 0, se utiliza el método convencional de distancia, el mismo que fue explicado en la sección 2. Mientras que al momento de obtener un valor de la resistencia de falla diferente de cero mediante la fórmula deWarrington es necesario aplicar la metodología propuesta en este artículo, donde luego de obtener los valores de voltajes y de corrientes medidos por los transformadores de instrumento se calcula la impedancia adaptativa considerando los valores establecidos con anterioridad.
Resultados
Para el análisis posterior se denomina R1 al relé conectado a las barras 9-6 y R2 al equipo de protección conectado en las barras 6-4, tal como lo muestra la Figura 2, su funcionamiento ha sido evaluado para diferentes situaciones de falla, con dos tipos de fuentes, la incorporación de la resistencia de falla y la variación en la potencia generación del parque eólico.
Resistencia de falla
Con el fin de verificar el funcionamiento óptimo del sistema de protección, se realizan pruebas de cortocircuito en las líneas L1 y L2 conectadas a un generador síncrono y con resistencia de falla de 0 y 25 Ω. En la Tabla 9 se observa que el ajuste convencional del relé de protección con Rf= 0Ω, no presenta errores en el tiempo de actuación. Mientras que cuando la Rf= 25Ω,
el relé R1 tiene una operación errónea cuando la falla se localiza a 80 y 90 % de la longitud de la línea. (Tabla 10)
Tabla 10 Operación del relé Siemens 7SA522 en sistemas convencionales considerando resistencia de falla
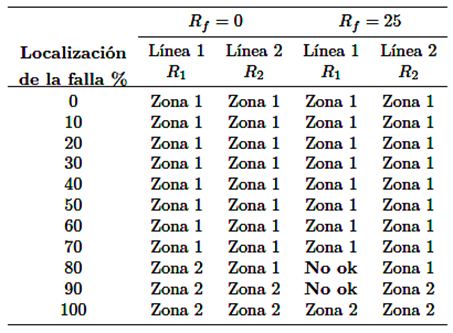
Potencia de generación eólica fluctuante
En la sección 3 se demuestra que al calcular eventos de cortocircuitos en las líneas de transmisión, que tienen como fuente de alimentación un parque eólico con potencia de generación variable y RF = 0, la impedancia vista por la protección se mantiene fija con la variación de potencia.
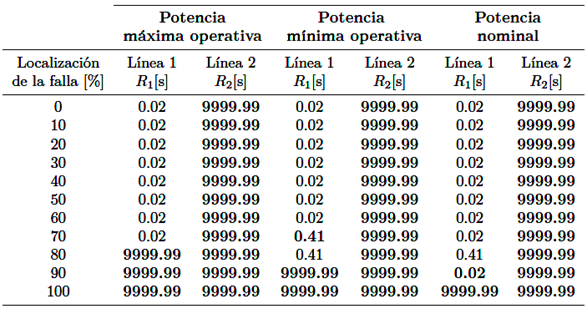
A continuación, se detallan los resultados obtenidos al calcular eventos de cortocircuito al tener una RF = 25Ω, cuando las líneas L1 y L2 se ven afectadas por una falla, los ajustes de los relés R1 y R2 en los tres escenarios de generación tienen errores de operación siendo la línea L2 la más afectada como lo muestran la Tabla 11.
Tabla 11 Operación de la protección de distancia ante la generación de potencia fluctuante del parque eólico con Rf= 25Ω
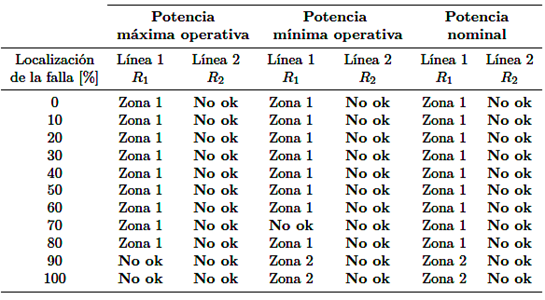
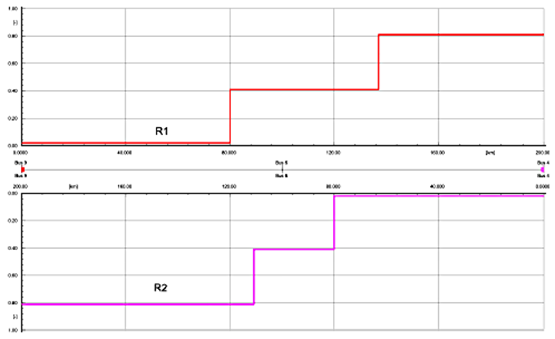
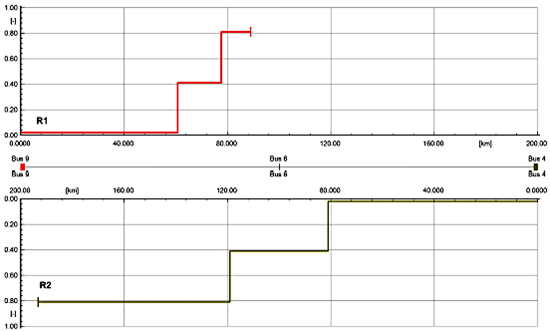
La Figura 8 presenta el diagrama distancia-tiempo de la protección de distancia, para el caso del relé R1 la zona 1 cubre el 80 % de la longitud de la línea, la zona 2 el 136 % y la zona 3 cubre la línea principal y adyacente, si se considera lo expuesto en las secciones anteriores existe un error en el alcance de la zona 2, ya que normalmente cubre solo el 120 % de la longitud de la línea. También el relé R2 presenta problemas, ahora la zona 2 alcanza solo un 112 % de la protección, lo que también es erróneo.
Hay que recordar que los tiempos de operación de la protección de distancia fueron detallados en la sección 3 (zonas de protección del relé), aplicando este criterio se ha determinado que el ajuste convencional opera en tiempos erróneos para diferentes puntos de localización de las fallas en las líneas dentro de la Tabla 12 estos valores están resaltados.
En la Figura 9 se presenta el plano R-X del relé (R2) que protege L2, luego de un cortocircuito con RF = 25Ω, donde se observa que la impedancia de falla en los tres escenarios evaluados no es identificada por la protección de distancia.
Método de ajuste cuadrilateral adaptativo
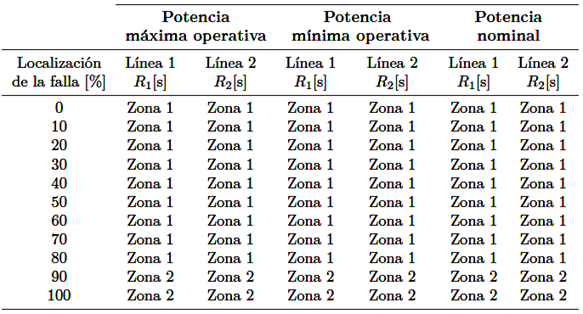
Anteriormente, se describieron los problemas que presenta la protección de distancia ante un cortocircuito que contempla la resistencia de falla, para corregir estos errores se aplica la metodología propuesta en este artículo, el método de ajuste cuadrilateral adaptativo, la Tabla 13 muestra los resultados de esta aplicación.
La Tabla 13 muestra el funcionamiento efectivo de la propuesta metodológica planteada para fallas en las líneas conectadas a un parque eólico.
Las zonas de protección de la metodología propuesta 𝑍 ∗𝑠𝑒𝑡 𝑎𝑑𝑎𝑝 (∗ = 1, 2, 3), han sido calculadas con la impedancia medida por cada relé luego de un cortocircuito y considerando la resistencia de falla, con el objetivo que el alcance de protección de R1 y R2 sea correcto.
En la Figura 10 se visualiza el ajuste para el relé R1 y R2, el alcance de protección se obtiene luego de aplicar las ecuaciones (4), (5), y (6), donde el límite máximo de actuación del relé estará dado por la impedancia medida por el equipo luego de una falla. Esta es la diferencia entre el método convencional y la nueva metodología, el ajuste de las zonas de protección ya no toma en cuenta la reactancia propia de la línea, sino que ahora usa valores de la impedancia vista por el relé luego de la falla, lo que hace que las zonas de protección se extiendan y así se corrige la operación indebida del relé.
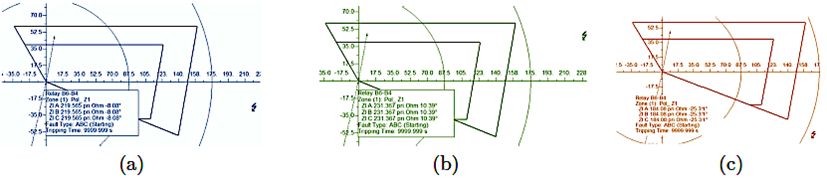
Al analizar la Tabla 12 se identifica que el relé R1 que protege a L1 actúa incorrectamente a partir del 70 % de la longitud de la línea, mientras que el relé R2 no cumple con la función de protección para la línea L2 cuando el sistema considera una resistencia de falla. Por esta razón es indispensable aplicar la metodología propuesta, como se muestra en la Figura 11, que al calcular una falla al 0 % de la línea L2 con a) potencia de generación máxima, b) potencia mínima y c) potencia nominal, la protección actúa en la zona 1 a un tiempo de 0.02s, a diferencia del ajuste convencional donde la impedancia de falla estaba fuera de zona.
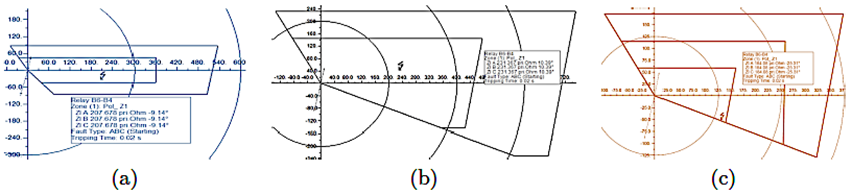
Figura 11 Cortocircuito en L2, aplicando el método de ajuste cuadrilateral adaptativo con a) Potencia máxima de operación; b) Potencia mínima de operación y c) Potencia nominal
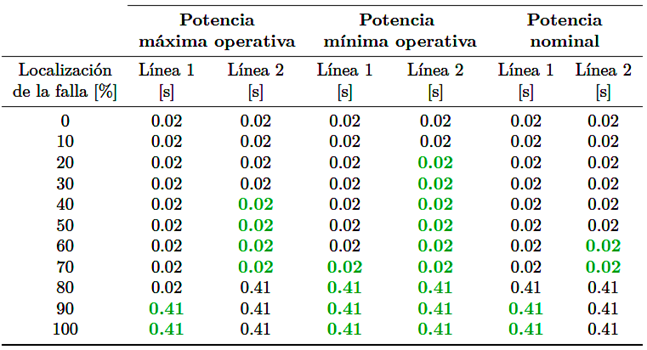
Los resultados de la Tabla 13 muestran el funcionamiento del método del ajuste adaptativo propuesto, ahora los relés tanto de la línea L1 como L2 identifican las fallas correctamente con su ubicación precisa y corrigen los tiempos incorrectos de actuación del relé convencional. (Tabla 14)
Discusión
El comportamiento de la protección de distancia ante la inserción de energías renovables no convencionales cambia cuando existe una resistencia de falla diferente de cero, debido a esto es probable la actuación errónea del relé, por ello la confiabilidad del sistema eléctrico de potencia se vería deteriorado. Para abordar este suceso, el artículo propone una protección con característica cuadrilateral con ajuste adaptativo, en los resultados de la simulación del caso de estudio se observa que, al calcular fallas internas, el método antes mencionado corrige los tiempos de actuación del relé. La metodología propuesta presenta resultados favorables a comparación del método de ajuste tradicional como:
Las consecuencias al momento de la inserción de una resistencia de falla son consideradas y se eliminan por completo debido a que la zona de protección tiende a ser mayor a la habitual.
El análisis de comportamiento de las fallas en este artículo es único para un parque eólico, por ello la estructura y la metodología de protección propuestas son aplicables a la inserción de ERNC (parque eólico).
Las diferentes zonas de protección del esquema propuesto se modifican para adaptarse a la variación de la impedancia adicional. Esta impedancia adicional (Zset) se debe a la resistencia de falla, por lo tanto, la corriente de falla cambia.
El esquema propuesto está diseñado para un único código de red donde se consideró un valor de resistencia de falla de 25 Ω, que fue calculado mediante la fórmula de Warrington.
Si comparamos los métodos de ajustes adaptativos para la característica Mho y cuadrilateral se asume que el último tiene más ventajas, ya que, dependiendo de la localización de la falla, la zona se puede expandir solo en el eje R-X o en ambos, es decir, tiene mayor alcance resistivo, pues no dependen el uno del otro. Por ello presenta mayor confiabilidad y seguridad al sistema eléctrico de potencia, a pesar de que esto requiera equipos con mayor tecnología y de mayor costo.
La metodología aplicada no estima la detección automática de fallas externas de los sistemas, para que esto sea posible se deberá modificar las características internas del relé por medio de programación exclusiva del mismo.
Conclusiones
El trabajo emplea un ajuste adaptativo para el sistema New England de 9 barras IEEE modificado, donde se produce la inserción de un parque compuesto por 33 generadores eólicos de 2.5 MW. Las zonas de operación de la característica cuadrilateral adaptativa se ajustan de acuerdo con la falla provocada, con la finalidad de evitar errores en la operación del relé SIEMENS 7SA522. En este trabajo se puede concluir lo siguiente:
El relé de distancia con ajuste cuadrilateral convencional funciona erróneamente cuando se da un cortocircuito trifásico que considere la resistencia de falla. Mientras que, el ajuste cuadrilateral adaptativo identifica correctamente las impedancias de falla desplazadas en eje X por el incremento de la resistencia de falla.
El método adaptativo propuesto muestra una respuesta favorable para diferentes escenarios de cortocircuito, con variación en el punto de falla, la resistencia de la falla y la oscilación de potencia del parque generador, demostrando que el relé opera en la zona de protección correcta.
El método planteado utiliza los datos de voltaje y corriente de los transformadores de instrumentación y calcula la impedancia de la línea hasta el punto de falla, el relé actúa de acuerdo con el ajuste de la protección, si la falla está localizada en el 80 % de la línea la zona 1 opera en t=0 segundos. Mientras que si la falla está en el 20 % de la línea adyacente al relé, opera la zona 2 en t=0.4 segundos. Finalmente, si el evento de cortocircuito se da al 100 % de la línea adyacente de donde está configurado el relé, actúa la zona 3 en t=0.8 segundos.
El método adaptativo propuesto muestra una respuesta favorable para diferentes escenarios de cortocircuito, con variación en el punto de falla, la resistencia de la falla y la oscilación de potencia del parque generador, demostrando que el relé opera en la zona de protección correcta.
El método planteado utiliza los datos de voltaje y corriente de los transformadores de instrumentación y calcula la impedancia de la línea hasta el punto de falla, el relé actúa de acuerdo con el ajuste de la protección, si la falla está localizada en el 80 % de la línea la zona 1 opera en t=0 segundos. Mientras que si la falla está en el 20 % de la línea adyacente al relé, opera la zona 2 en t=0.4 segundos. Finalmente, si el evento de cortocircuito se da al 100 % de la línea adyacente de donde está configurado el relé, actúa la zona 3 en t=0.8 segundos.