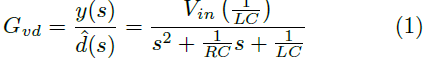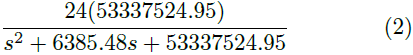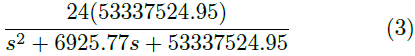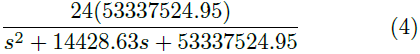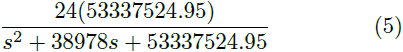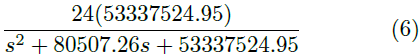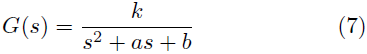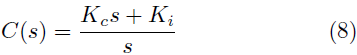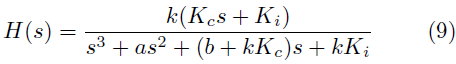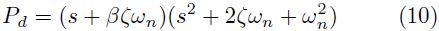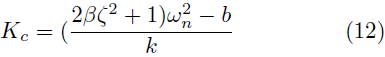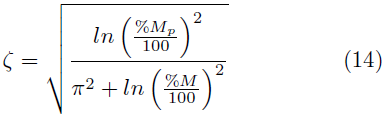Forma sugerida de citación:
Olivar- Castellanos, G. S.; Vela- Valdés, L. G. y López López, L. y Aguayo- Alquicira, J. “Control por ganancias programadas aplicado a un convertidor DC-DC para la regulación de la intensidad luminosa de una lámpara LED, “Ingenius, Revista de Ciencia y Tecnología, N.° 29, pp. 66-78, 2023. DOI: https://doi.org/10. 17163/ings.n29.2023.06
1. Introducción
A lo largo del tiempo, la iluminación ha presentado diversos avances tecnológicos, como la incorporación del LED (diodo emisor de luz) en diferentes aplicaciones. Esto se debe principalmente a que el LED presenta un bajo consumo, fiabilidad y un mayor tiempo de vida útil en comparación con otras tecnologías, lo que provoca que sea una opción sostenible, práctica y funcional para lograr un ahorro de energía [1].
Dentro de esta tecnología, algunas aplicaciones son tan sencillas en donde basta con el control del encendido y apagado de la lámpara LED, pero muchas otras requieren regular la iluminación entre 0 % y 100 %, a menudo, con una resolución fina [2]. Existen distintas arquitecturas para los controladores LED; su objetivo es responder a los requisitos y limitaciones impuestas por las diferentes aplicaciones de la iluminación, como iluminación interior/exterior, lámparas de invernadero, señales de tráfico, etc.
Los controladores LED suelen derivarse y adaptarse a partir de topologías básicas de convertidores AC-DC y/o DC-DC para integrar funciones como el control preciso de la potencia o la regulación de la intensidad luminosa [3].
Independientemente de la complejidad, todos estos sistemas de conversión de energía de potencia tienen en común la adopción de al menos una etapa de conversión DC-DC. Las topologías de convertidores DC-DC más comunes empleadas en el desarrollo de drivers LED incluyen convertidores buck, boost, flyback, sepic y/o medio puente [3].
Sin embargo, existen aplicaciones en donde es indispensable la incorporación de esquemas de control, con el fin de mejorar la precisión y la respuesta del sistema. Para ello, es común utilizar esquemas de control clásico, como los trabajos realizados en [4,5,6,7]. En estos trabajos, estos esquemas son suficientes dado que se trata de aplicaciones de regulación, es decir, se trabaja en un solo punto de operación del LED, garantizando la dinámica deseada alrededor de dicho punto.
Por otro lado, existen aplicaciones más complejas, en donde se requiere estabilidad en todo el rango de operación del LED, dando lugar a un control de seguimiento. En estas aplicaciones cobra importancia el hecho de que el LED es un dispositivo no lineal, puesto que al tener esta característica y requerir que trabaje en todo su rango de operación con precisión, se hace indispensable el uso de un control no lineal.
Para dar solución a esto, autores han incorporado esquemas como redes neuronales [8], lógica difusa [9,10,11], o incluso combinación de esquemas de control como el PID difuso [12]. Sin embargo, la mayoría de estos trabajos se centran en garantizar un bajo error en estado estable, y para esos casos puede ser suficiente un único control lineal, como el trabajo presentado en [2]. No obstante, existen aplicaciones en donde, además de garantizar un bajo porcentaje de error, es necesario cuidar el máximo sobretiro.
Debido a esto, en la literatura se presenta otra alternativa para dar solución a las no linealidades presentes en el LED, como lo es la técnica de ganancias programadas, presentada en [13], en donde se propone el control de la intensidad luminosa de un arreglo LED mediante un convertidor Flyback y la técnica de ganancias programadas, sin embargo, no se le da una aplicación en específico y la sintonización del controlador es de forma empírica.
La técnica de ganancias programadas permite utilizar herramientas lineales que aproximen la dinámica no lineal del sistema, siendo posible ajustar de manera previa un controlador para diversos puntos de operación, y posteriormente, actualizar los parámetros de este a partir de dichos diseños y según el punto de trabajo en el que se encuentre el proceso [14,15].
El objetivo de este trabajo es diseñar una fuente de alimentación que permita regular la intensidad luminosa de una lámpara LED en un amplio rango de operación, con bajo porcentaje de error en estado estable y cuidando no dañar la lámpara con grandes sobretiros, para lo cual se toma como caso de estudio las lámparas de protección ocular.
Este artículo se encuentra organizado de la siguiente manera: la sección 2 se refiere a metodología para el desarrollo del sistema, la cual comprende desde la caracterización de la lámpara hasta la sintonización de esquemas de control. En la sección 3 se analizan los resultados obtenidos y finalmente, en la sección 4 se abordan las conclusiones y los trabajos futuros.
1.1. Caso de estudio: Lámpara de protección ocular
De acuerdo con la Organización Mundial de la Salud (OMS), al menos 2200 millones de personas tienen deficiencia visual o ceguera, y más de 1000 millones podrían haberse evitado [16]. Estudios demuestran que para el año 2050 el 50 % de la población mundial padecerá miopía, y la visión humana se enfrentará a una prueba cada vez más severa [17].
Una de las principales causas de la deficiencia visual es la miopía, la cual puede prevenirse teniendo los niveles de iluminación adecuados. Debido a esto, la OMS recomienda mantener niveles de iluminancia en 500 lx en las áreas de estudio o trabajo, de preferencia con fuentes de luz blanca, con el fin de prevenir este padecimiento [18].
Esto no es una tarea sencilla, puesto que fuentes de iluminación externas como la iluminación natural, o incluso otras fuentes de iluminación artificial, perturban la iluminación en el área deseada, provocando que no se tengan los niveles recomendados.
Con base en esto, es necesario un sistema capaz de regular la intensidad luminosa que proporciona una lámpara de protección ocular, de manera que esta complemente a la iluminación exterior, manteniéndose el nivel de iluminancia en los 500 lx recomendados por la OMS.
Tomando esto en cuenta, se realiza el diseño de un convertidor CD-CD con esquemas de control PI clásico, PI difuso y ganancias programadas, con el propósito de seleccionar el esquema de control adecuado para este caso de estudio y con ello, demostrar que un esquema de control lineal no es apto para tareas de seguimiento en iluminación LED.
2. Materiales y métodos
El LED es un dispositivo en el que su intensidad luminosa depende de la corriente que circula a través de él [13]. No obstante, esta corriente depende de la tensión entre sus terminales. Por ende, para variar la intensidad luminosa de un LED resulta práctico realizar variaciones de tensión. Para ello, es necesaria una fuente de alimentación capaz de realizar y soportar estas variaciones.
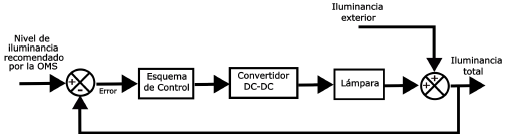
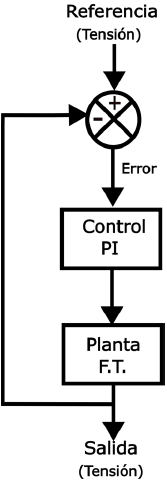
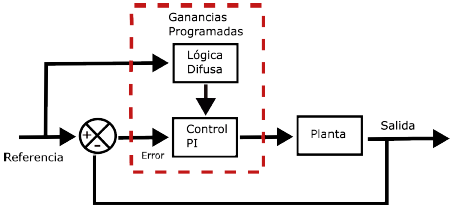
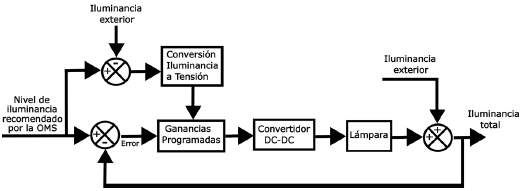
Debido a esto, se propone implementar un convertidor DC-DC que cumpla estas características. Además, para garantizar los niveles recomendados por la OMS, se debe incorporar un esquema de control. Esto se representa mediante el diagrama a bloques mostrado en la Figura 1.
Al garantizar que la tensión en la lámpara es la deseada se asegura que el nivel de iluminancia sea el requerido. Por ello, para simplificar el sistema se sintonizan los distintos controladores tomando como referencia un valor de tensión.
Todo este proceso se muestra en los siguientes apartados, realizándose la simulación del sistema con los controladores en Simulink/Matlab.
2.1. Caracterización de la lámpara
Para lograr que la lámpara de protección ocular complemente la iluminación natural, es necesario diseñar una fuente de alimentación con un controlador que permita regular la iluminancia dependiendo de las variaciones que se tengan en la luz natural.
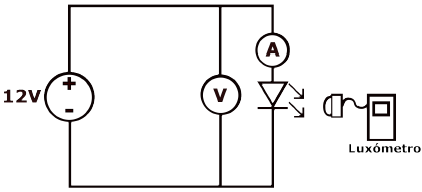
El primer paso es realizar la caracterización de la lámpara. Para esto, se sigue el diagrama esquemático mostrado en la Figura 2. Se sabe que la lámpara se alimenta con una tensión de 12 VDC, por ello se conecta a dicha tensión y se realizan variaciones descendentes, midiendo los cambios en tensión, corriente e iluminancia.
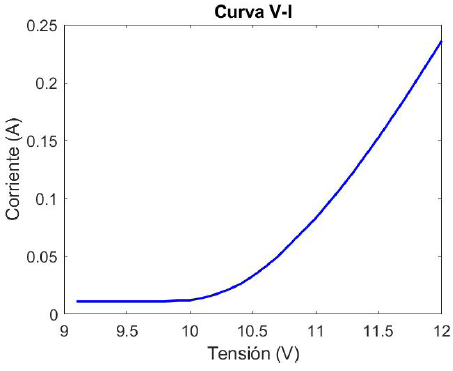
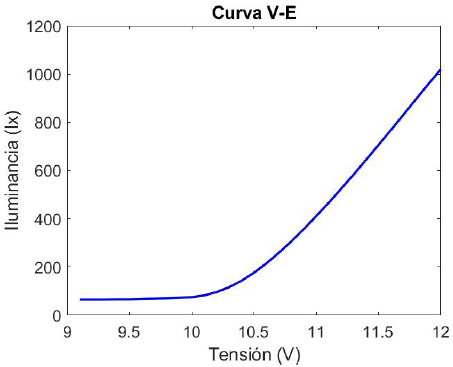
Graficando los datos obtenidos, se obtiene la curva V-I (tensión-corriente) de la lámpara mostrada en la Figura 3, mientras que en la Figura 4 se muestra la curva V-E (tensión-iluminancia).
2.2. Diseño del convertidor DC-DC
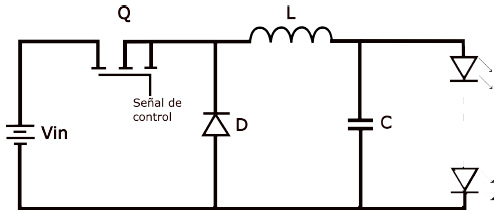
El convertidor Buck es utilizado en aplicaciones en donde la carga requiere tensiones menores que la tensión de entrada del convertidor. Su implementación es sencilla debido a la poca cantidad de componentes, además, su control es simple, puesto que la relación entre la tensión de salida y la de entrada es proporcional al ciclo de trabajo de la señal de control [13].
Debido a lo anterior, se elige el convertidor Buck como fuente de alimentación de la lámpara. Para su diseño, se definen las especificaciones mostradas en la Tabla 1, propuestas a partir de la caracterización. En la Figura 5 se muestra la topología de este convertidor.
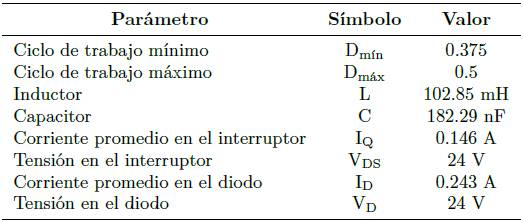
A partir del análisis y de las ecuaciones mostradas por Gamboa [19], se realiza el cálculo y selección de los componentes. El valor de estos se muestra en la Tabla 2.
2.3. Funciones de transferencia
Para la obtención de las funciones de transferencia (F. T.) se debe tener claro que la carga del convertidor es variable, puesto que el LED trabaja en diferentes puntos de operación según se requiera. Por ello, no es posible obtener una sola F. T. lineal que represente toda la dinámica del sistema.
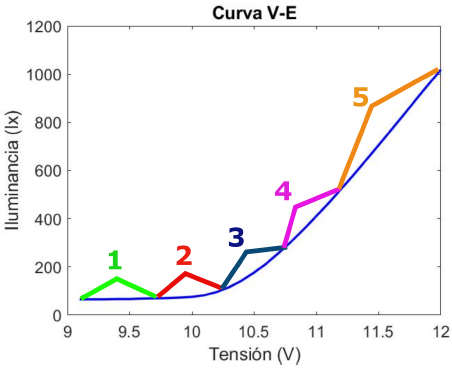
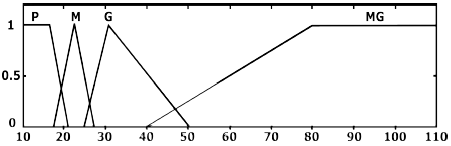
Debido a lo anterior, y para facilitar el diseño de los controladores, se secciona la curva V-E de la lámpara en cinco rangos aproximadamente lineales, como se muestra en la Figura 6. Al dividir esta curva, es posible obtener cinco F. T. que aproximen la dinámica en cada uno de los rangos.
Posteriormente, dado que se tienen definidos los puntos de operación, es posible obtener la F. T. a partir de la función control-salida característica de un convertidor Buck, mostrada en la Ecuación (1).
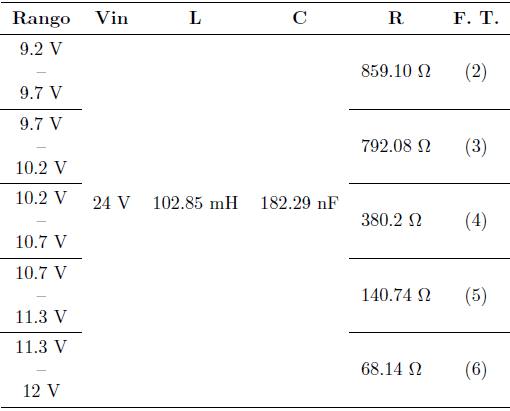
Puesto que el convertidor trabaja en todo el rango de operación de la lámpara, el valor de R en la Ecuación (1) es variable. Por ello, se calcula una R promedio en cada uno de los rangos definidos, obteniéndose de esta manera una F. T. diferente para cada rango de operación. Los parámetros para estas F. T. se muestran en la Tabla 3, mientras que las funciones se muestran en las Ecuaciones (2),(3),(4),(5),(6).
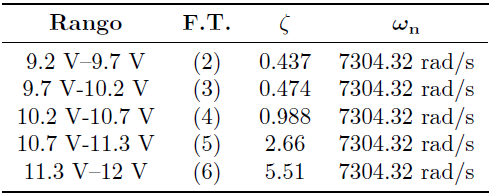
Es importante mencionar que el hecho de que se tengan F. T. distintas para cada rango de operación, tiene como consecuencia que se consigan dinámicas diferentes en cada uno de ellos. Esto se debe a que se tiene un distinto factor de amortiguamiento (ζ) en cada rango, a pesar de tener la misma frecuencia natural (ω n ). Esto se detalla en la Tabla 4.
2.4. Sintonización de un control PI
Debido a que el esquema de control PI es de los más utilizados en aplicaciones con convertidores DC-DC, se realiza la sintonización de este para validar y comparar su funcionamiento en la regulación de la iluminancia de una lámpara de protección ocular.
El controlador es sintonizado para el rango de operación intermedio, correspondiente a la F. T. de la Ecuación (4).
Para la sintonización se utiliza la metodología de asignación de polos. Se parte de que la ecuación característica de una F. T. de segundo orden se puede simplificar como se muestra en la Ecuación (7).
Además, se sabe que la F. T. de un control PI es de la forma mostrada en la Ecuación (8).
Entonces, al cerrar el lazo de la planta con el controlador, se tiene la F. T. mostrada en la Ecuación (9).
Por lo tanto, se debe definir una asignación de polos con base en un sistema de tercer orden con dos polos complejos conjugados y un polo real, de la forma mostrada en la Ecuación (10), donde β representa un factor de proporcionalidad que relaciona la distancia entre el polo real con respecto a los polos complejos conjugados.
Entonces, igualando (10) con el denominador de la F. T. en lazo cerrado de la Ecuación (9) y despejando las incógnitas, se tienen tres ecuaciones útiles para el cálculo de las ganancias de un control PI. La forma de calcular se presenta en la Ecuación (11), mientras que en las Ecuaciones (12) y (13) se presenta el cálculo de la ganancia proporcional (K c ) y la ganancia integral (K i ) respectivamente.
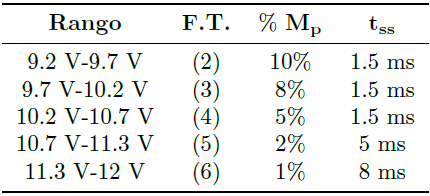
De esta manera, se puede calcular las ganancias del controlador PI a partir de un factor de amortiguamiento (ζ) y de una frecuencia natural (ω n ) deseados. Es importante mencionar que es posible calcular ζ y ωn a partir de las Ecuaciones (14) y (15), definiendo un máximo sobretiro (M p ) y un tiempo de asentamiento (tss). En este caso, se propone un M p no mayor al 5 % y se busca un tss de 1 ms.
Por lo tanto, se obtiene que β = 1.608, K c = 0.247 y K i = 168.7537. Implementándose esto como se muestra en la Figura 7.
2.5. Sintonización de un control PI difuso
Es común que el control por lógica difusa tenga un grado de incertidumbre, debido a que este puede ser expresado mejor como un control a través de palabras que interpretan el sentido común, en lugar de números, o bien sentencias en lugar de ecuaciones [20]. Sin embargo, las variables de los procesos no se miden en sentido común, sino en números.
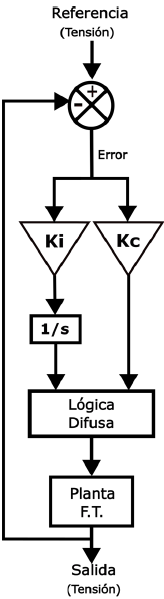
Para corregir este problema, resulta conveniente incorporar las ganancias de un control PI, logrando así corregir numéricamente las falencias de la interpretación difusa. El diagrama a bloques que representa este esquema de control se muestra en la Figura 8.
Para el diseño del controlador difuso se deben tener claras las variables de entrada y de salida. En este caso, se tiene como variables de entrada el error y la integral del error, y como salida está el ciclo de trabajo, puesto que es la variable que requiere la planta.
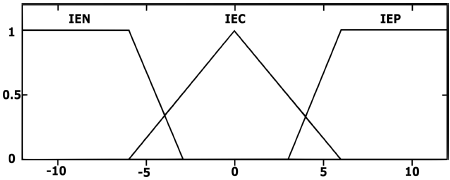
Dado que el error se obtiene a partir de la comparación de la salida del convertidor, la cual es una tensión máxima de 12 V, se define un universo de discurso de {–12, 12} para ambas entradas. Es importante mencionar que se define un universo que contempla números negativos, puesto que es posible obtener una diferencia tanto positiva como negativa entre la salida y la referencia.
Las variables lingüísticas para la señal de error son definidas como:
Mientras que las variables lingüísticas definidas para la integral del error son:
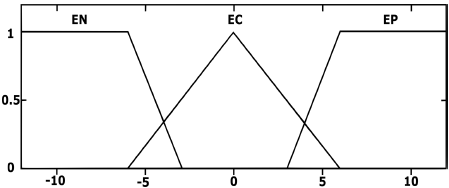
Una vez que se han establecido las distintas variables lingüísticas de las entradas, así como sus respectivos universos de discurso, se definen los conjuntos difusos como se muestra en la Figura 9 y Figura 10, respectivamente.
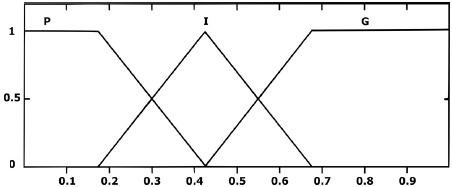
Por su parte, la salida del bloque difuso es el ciclo de trabajo, donde su universo de discurso se define de {0, 1} dado que es el intervalo en el que este opera.
Las variables lingüísticas definidas para el ciclo de trabajo son:
El conjunto difuso del ciclo de trabajo se muestra en la Figura 11.
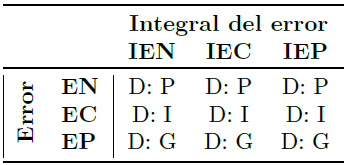
Una vez que se tienen definidos los distintos conjuntos difusos, se asignan las reglas de control. Para cada salida se asigna una variable lingüística según corresponda, en función de las posibles combinaciones de las entradas. El conjunto de reglas se muestra en la Tabla 5.
Para verificar el funcionamiento del controlador PI difuso, se cargan los conjuntos difusos definidos, así como las reglas difusas en la herramienta fuzzyLogicDesigner
2.6. Control por ganancias programadas
El control por ganancias programadas consiste en ajustar de manera previa un controlador para diversos puntos de operación, y posteriormente, actualizar los parámetros de este a partir de dichos diseños y según el punto de trabajo en el que se encuentre el proceso [14, 15].
Uno de los métodos más utilizados para la selección de las ganancias es la lógica difusa, conformando así un tipo de control conocido como programación de ganancias difusa (FGS: Fuzzy Gain Scheduling) [13].
En este sentido, la lógica difusa se encarga de la variación en tiempo real de las ganancias, con la ventaja de que permite suavizar la transición entre los controladores, determinando valores intermedios de las ganancias y reduciendo los cambios drásticos que puedan afectar al controlador y a la planta.
Considerando lo anterior, se tiene el diagrama a bloques de la Figura 12, en el cual se muestra el sistema a implementar. El control de ganancias programadas diseñado está compuesto por un bloque de lógica difusa, encargado de seleccionar las ganancias del control PI, dependiendo del punto de operación requerido.
Puesto que el rango de operación de la lámpara LED se ha seccionado en cinco intervalos, se tienen 5 F. T. diferentes, para las cuales se debe diseñar un control PI distinto.
Debido a que cada rango de operación presenta una dinámica diferente, se proponen especificaciones de diseño distintas para cada uno de los rangos.
Un punto importante a tener en cuenta es que no se debe tener un sobretiro muy alto en el rango de operación de 11.3 V – 12 V, dado que este podría llegar a dañar la lámpara LED. Tomando esto en cuenta, en la Tabla 6 se muestran las especificaciones de diseño para cada controlador.
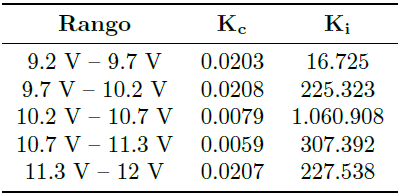
Para la sintonización del controlador se utiliza la metodología de asignación de polos descrita en la sección 2.4, obteniéndose las ganancias mostradas en la Tabla 7.
Por otro lado, para el selector de las ganancias del control PI se realiza el diseño de un control por lógica difusa.
Para este caso, resulta conveniente tener como variable de entrada la señal de referencia, ya que esta define el rango de operación en el que se trabaja. Así mismo, se definen como variables de salida las ganancias Kc y Ki, dado que estas variables cambian dependiendo del rango de operación.
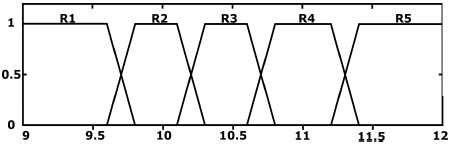
Tomando en cuenta el rango de operación, se define un universo de discurso de la variable de entrada de {9, 12}. Por su parte, las variables lingüísticas para los rangos de operación se definen como:
Una vez que se han establecido las variables lingüísticas de la entrada, se definen los conjuntos difusos como se muestra en la Figura 13.
Para los conjuntos difusos de salida, se define que el universo de discurso para Kc es de {0.004, 0.022} y para Ki es de {10, 110}.
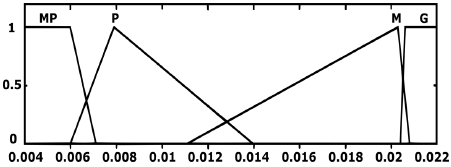
Mientras tanto, para las variables lingüísticas se observa que existen dos rangos en los que se tienen ganancias muy similares, por lo que se promedian y se definen como una sola, por lo tanto, las variables lingüísticas para Kc quedan definidas como:
Por su parte, las variables lingüísticas para Ki se definen como:
Entonces, el conjunto difuso para la ganancia Kc queda definido como se muestra en la Figura 14, mientras que el conjunto difuso de la ganancia Ki se muestra en la Figura 15.
Para el conjunto de reglas, se asigna una variable lingüística en función de la entrada para cada salida, como se muestra en la Tabla 8.
No se debe perder de vista que se desea controlar el nivel de iluminancia en un área de estudio o trabajo, manteniendo los 500 lx recomendados por la OMS. En el diseño de estos controladores se trabajó con niveles de tensión para facilitar su diseño, por lo que se debe de adecuar el sistema, realizando conversiones de tensión a iluminancia. Esto se puede realizar a partir de la caracterización de la lámpara, modificándose el diagrama a bloques del sistema, como se muestra en la Figura 16.
3. Resultados y discusión
Para la validación de los esquemas de control diseñados, estos se simulan con tres funciones de transferencia distintas: la función intermedia, mostrada en la ecuación (4), y las funciones de los extremos del rango de operación de la lámpara, mostradas en las ecuaciones (2) y (6).
Al simular la F. T. central con el control PI se obtiene la respuesta mostrada en la Figura 17. Se observa que se tiene un error en estado estable de 0 %, un sobretiro máximo de 4.6 % y un tiempo de estabilización de aproximadamente 1.8 ms (Figura 17).
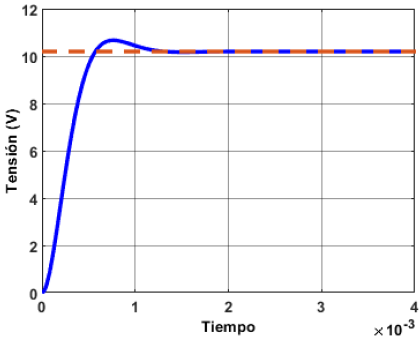
Figura 17. Respuesta de la función de transferencia del rango de operación central con un esquema de control PI
No obstante, al simular el mismo esquema de control con las mismas ganancias en los rangos de operación de los extremos, se obtienen dinámicas no deseadas, principalmente en el rango superior, puesto que el máximo sobretiro excede los 12 V de alimentación de la lámpara. Las respuestas de estas F. T. ante el esquema de control se muestran en las Figuras 18 y 19 respectivamente.
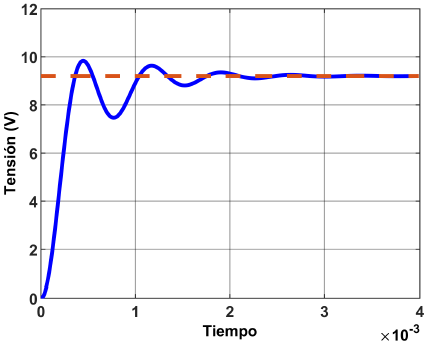
Figura 18. Respuesta de la función de transferencia del rango de operación inferior con un esquema de control PI
Aunque en los tres casos se alcanza un error en estado estable de 0 %, un sobretiro mayor a 12 V podría dañar la lámpara, razón por la cual un único control PI resulta poco apto para la aplicación.
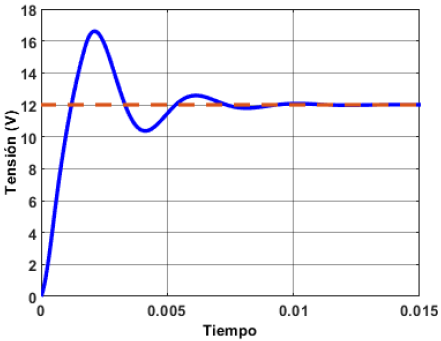
Figura 19. Respuesta de la función de transferencia del rango de operación superior con un esquema de control PI
Por otro lado, al simular el esquema de control PI difuso se obtiene una mejoría en la respuesta del sistema en el rango de sintonización, puesto que se reduce notoriamente el máximo sobretiro, como se muestra en la Figura 20. Además, se garantiza un error en estado estable de 0 % y se alcanza un tiempo de estabilización de 1.2 ms.
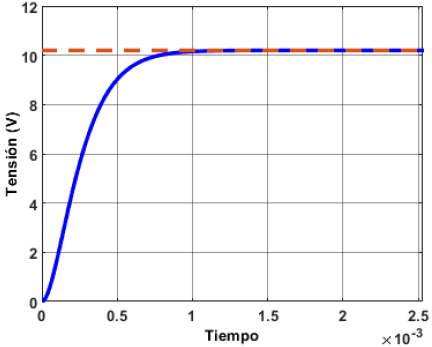
Figura 20. Respuesta de la función de transferencia del rango de operación central con un esquema de control PI difuso
No obstante, al aplicar el mismo controlador en los rangos de operación de los extremos se obtienen respuestas no deseadas, puesto que a pesar de que no se tiene sobretiro, el error en estado estable es mayor al 2 %, como se muestra en las Figuras 21 y 22.
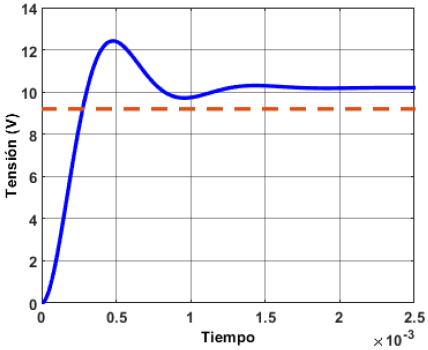
Figura 21. Respuesta de la función de transferencia del rango de operación inferior con un esquema de control PI difuso
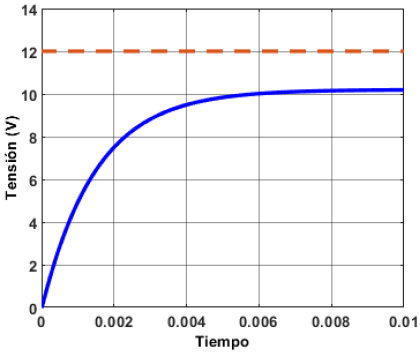
Figura 22. Respuesta de la función de transferencia del rango de operación superior con un esquema de control PI difuso
Mientras tanto, al simular el esquema de control por ganancias programadas se obtiene la respuesta deseada en cada uno de los rangos. En la Figura 23 se muestra la respuesta en el rango de operación central, mientras que la respuesta del rango inferior y superior se muestran en las Figuras 24 y 25 respectivamente.
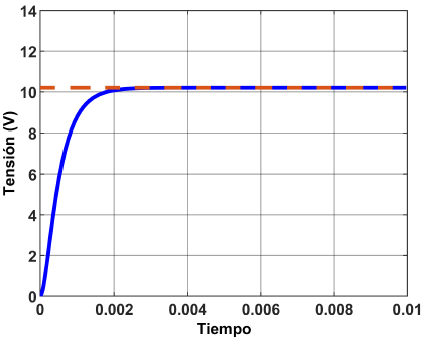
Figura 23. Respuesta de la función de transferencia del rango de operación central con un esquema de control de ganancias programadas.
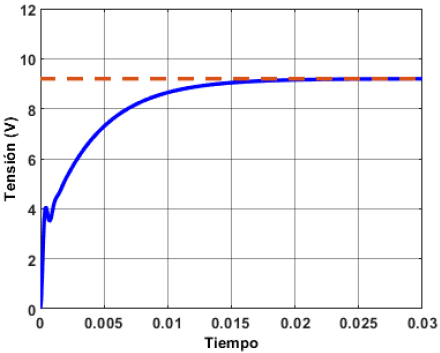
Figura 24. Respuesta de la función de transferencia del rango de operación inferior con un esquema de control de ganancias programadas
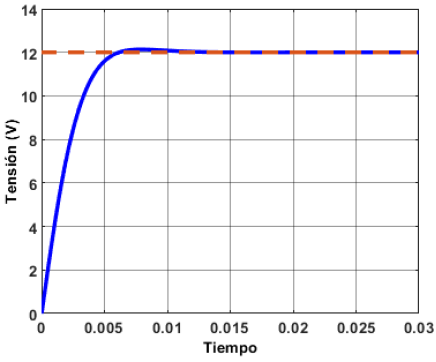
Figura 25. Respuesta de la función de transferencia del rango de operación superior con un esquema de control de ganancias programadas
Se observa que en todas las respuestas se tiene un error en estado estable de 0 %, además, se tienen sobretiros menores al 2 %. No obstante, el tiempo de estabilización aumenta.
La comparación de las respuestas obtenidas con los tres esquemas de control se muestra en la Tabla 9.
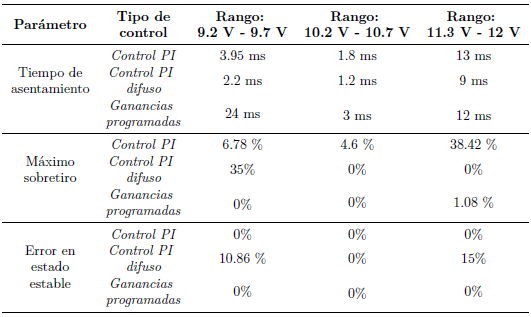
Tabla 9. Comparación de las respuestas con los esquemas de control PI, PI difuso y ganancias programadas
Es importante mencionar que el máximo sobretiro y el tiempo de estabilización para los cuales se sintonizó el control por ganancias programadas difieren de las especificaciones de diseño. Esto se debe principalmente a los efectos del polo real y del cero que se produce al cerrar el lazo.
Sin embargo, estos efectos no perjudican la dinámica deseada, sino que la benefician, lográndose sobretiros muy pequeños. El parámetro en el que se nota el efecto del polo real y del cero es en el tiempo de estabilización, sin embargo, este tiempo es del orden de milisegundos, que para efectos de iluminación y del convertidor no cobra relevancia.
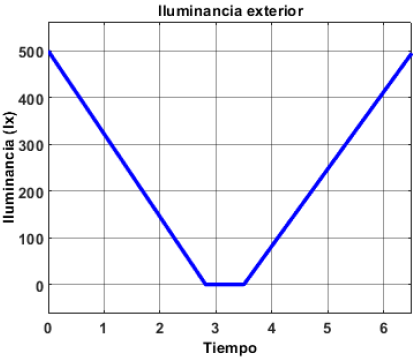
Con base en lo anterior, el control por ganancias programadas presenta una mejor respuesta en todo el rango de operación de la lámpara, por lo que se simula incorporando el modelo de la lámpara. El patrón de iluminancia exterior se toma a partir de los niveles de irradiancia solar en la ciudad de Cuernavaca, Morelos, México, en un día de primavera, recopilados de la base de datos del Instituto Nacional de Ecología y Cambio Climático [21]. Este patrón se muestra en la Figura 26.
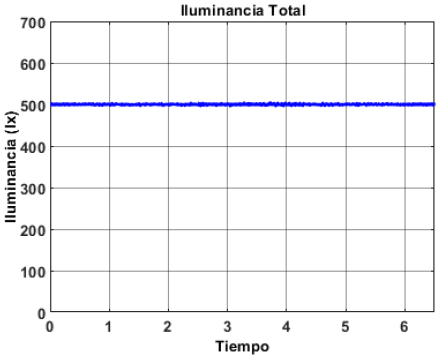
La lámpara de protección ocular debe complementar la iluminación ante los cambios en la iluminación exterior, con el fin de mantener los 500 lx recomendados por la OMS. La respuesta del sistema ante los cambios en la iluminación exterior se muestra en la Figura 27.
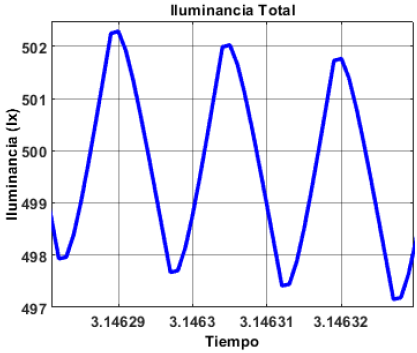
Se observa que a pesar de que la iluminación exterior cambie, el nivel de iluminancia total se mantiene en los 500 lx recomendados por la OMS. No obstante, en el momento en el que la iluminación exterior es mínima se observa que se tiene un mayor rizo. Este rizo se muestra en la Figura 28 y se debe a que en este punto el convertidor debe proporcionar una mayor tensión a la lámpara, y por consiguiente se tiene un mayor rizo de tensión debido a efectos del capacitor de salida del convertidor. Sin embargo, este rizo se encuentra alrededor del 1 %, por lo que se encuentra dentro de los márgenes aceptables de la teoría de control.
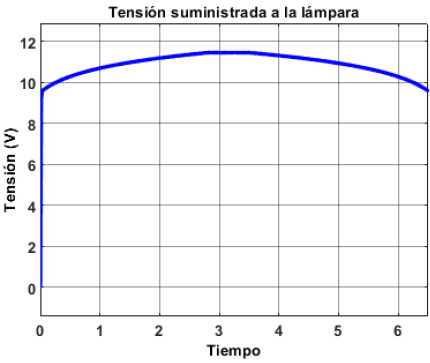
Por otro lado, en la Figura 29 se muestra la tensión suministrada por el convertidor diseñado. Se observa que la tensión se mantiene dentro de los rangos de operación, de manera que se garantiza no dañarla. Además, se muestra que la lámpara no trabaja en un solo punto de operación, sino que demanda diferentes niveles de tensión al convertidor según cambia el nivel de iluminancia exterior.
4. Conclusiones
En la actualidad existen distintas aplicaciones para las lámparas LED, no obstante, algunas de ellas requieren de precisión al variar la intensidad luminosa, como el caso de las lámparas de protección ocular.
Debido a esto, en este trabajo se mostró la simulación de un convertidor DC-DC con tres esquemas de control para variar la iluminancia de una lámpara de protección ocular, con el fin de mantener los 500 lx recomendados por la OMS para prevenir enfermedades oculares, en donde fuentes de iluminación externas perturban a la iluminación proporcionada por la lámpara.
Un esquema de control PI clásico es capaz de garantizar un error en estado estable de 0 % en todo el rango de operación de la lámpara, sin embargo, no garantiza niveles de sobretiro adecuados para el funcionamiento de la misma.
Por otro lado, el esquema de control PI difuso diseñado es capaz de garantizar que no se excedan los niveles de tensión soportados por la lámpara, sin embargo, sí se cambia el punto de operación, el error en estado estable aumenta.
Por su parte, el control por ganancias programadas diseñado es una combinación entre controladores PI y lógica difusa, puesto que esta última se utiliza como selector de ganancias, logrando así ajustar la ganancia del controlador dependiendo del punto de operación en el que se encuentre el sistema. De esta manera, se logra garantizar un error en estado estable de 0 % y disminuir el máximo sobretiro.
Al simular el control por ganancias programadas incorporando el modelo de la lámpara, se logra mantener el nivel de iluminancia en 500 lx, de manera que la lámpara complementa a la iluminación exterior, cumpliéndose lo recomendado por la OMS. Además, se garantiza que el convertidor DC-DC no proporcione niveles de tensión por encima del rango de operación de la lámpara, con lo que se comprueba que se regula la intensidad luminosa de la lámpara LED, con precisión y cuidando no dañarla, a diferencia de otros trabajos que se enfocan en el control en un solo punto de operación con un control lineal.
Cabe mencionar que como trabajo futuro es posible mejorar el rizo presente en la iluminancia total, aumentando el valor del capacitor de salida del convertidor, sin embargo, esto modifica las F. T. y, por consiguiente, las dinámicas obtenidas.
Por su parte, el control por ganancias programadas puede incorporarse en distintas aplicaciones, por lo que se recomienda su validación con otros casos de estudio en aplicaciones de iluminación.