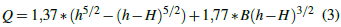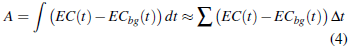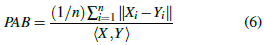2.1 Área de estudio

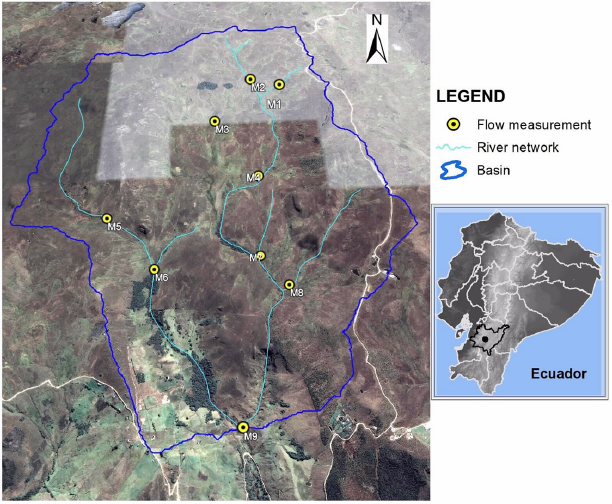
El estudio se llevó a cabo en el Observatorio Ecohidrológico de Zhurucay (Figura 1), que se encuentra en un ecosistema de páramo en el sur de Ecuador. El río Zhurucay es un afluente del río Jubones que desemboca en el océano Pacífico (^{Mosquera y col., 2015}; ^{Correa y col., 2019}). La cuenca del río Zhurucay tiene un área de drenaje de 7,53 km² y un rango altitudinal entre 3400 y 3900 m s.n.m. La precipitación media anual es de 1345 mm con lluvias bien distribuidas durante el año, y se caracterizan por ser eventos frecuentes y de baja intensidad (^{Padrón, Crespo y Célleri, 2015}). La evapotranspiración anual (ETa) es de 622 mm (^{Ochoa-Sánchez y col., 2019}). La vegetación está compuesta principalmente por pastos de tussock (72% de la cuenca) y plantas de cojín (24%); las especies forestales como Polylepis y Pinos cubren el resto de la cuenca (^{Correa y col., 2017}; ^{Carrillo-Rojas y col., 2019}).

Figura 1.  Área del estudio: Observatorio ecohidrológico de Zhurucay. M9: vertedero rectangular. M1 a M8: vertederos compuestos. 

2.2 Vertederos

El monitoreo de caudales en Zhurucay sigue un enfoque anidado, utilizando 9 vertederos situados aguas arriba o abajo de las confluencias. Estos vertederos son o bien vertederos compuestos de muesca en V y cresta afilada (que consisten en una parte de muesca en V (sección triangular) y una parte rectangular, y se denominan M1 a M8) o un vertedero rectangular de cresta afilada (M9). Existe descarga libre aguas abajo de los vertederos (es decir, aire bajo la lámina de descarga sobre el vertedero), lo cual es un requisito para utilizar la ecuación del vertedero (Figura 2). Cada vertedero tiene un sensor de nivel de agua con una precisión de 1 mm, y registra datos cada 5 minutos. En los arroyos más pequeños (de 0,2 a 3,28 km² ) se colocaron vertederos de muesca en V compuesta, ya que permiten medir con precisión descargas muy bajas (^{Célleri, De Bièvre y Ochoa, 2012}). La construcción y las especificaciones de los vertederos se pueden encontrar en ^{Bergmann (1963)} y ^{United States Bureau of Reclamation (2001)}.

Figura 2. Ejemplos de un vertedero rectangular (izquierda) y de un vertedero compuesto (muesca en V - rectangular) (derecha) en la zona de estudio. 

Existen ecuaciones específicas para los vertederos en V y rectangulares. Para los vertederos de muesca en V, cuando la descarga se produce dentro de la sección triangular, se utiliza la ecuación de Kindsvater (Ecuación 1) ofrecida por el ^{United States Bureau of Reclamation (2001)}. Para los vertederos rectangulares suprimidos de cresta aguda, ^{Kindsvater y Carter (1959)} desarrollaron la ecuación (Ecuación 2). Los mismos autores crearon una ecuación para estimar la descarga que pasa por un vertedero compuesto, que consiste en una parte con muesca en V (con un ángulo de muesca de 90 grados) y una parte rectangular (Ecuación 3).

Para las ecuaciones 1 a 3: Q es el caudal (m ³ /s); h es la altura del agua desde el vértice de la muesca en V (m), medida en un punto situado a una distancia horizontal de 4H aguas arriba del vertedero; H es la altura de la muesca en V (m); B es la anchura combinada (m) de las partes rectangulares del vertedero; L es la anchura (m) del vertedero rectangular; y 1,37 y 1,77 son los coeficientes teóricos de descarga para la muesca en V (DCvn) y la sección rectangular (DCr), respectivamente. La H de todos los vertederos de Zhurucay es de 30 cm. Para este estudio se han considerado descargas bajas hasta 5,5 l/s (h<11 cm); descargas medias entre 5,5 y 67,5 l/s (11 ≤ h < 30 cm), y valores superiores a 67,5 l/s (h ≥ 30 cm) para descargas altas.

3.1 Métodos de medición de la descarga

Se utilizaron tres métodos de medición de caudales para estimar las curvas altura-descarga: volumétrico (volumen-tiempo), velocidad-área (medidor de corriente o correntómetro) y método de dilución. En esta sección, se detalla cada método. El método de dilución se describe con más detalle por ser el menos común.

3.1.3 Método químico (Dilución salina)

Este método se basa en la capacidad de la corriente para diluir uniformemente el trazador en el agua (^{Rantz, 1982}). Los ríos y arroyos de montaña tienen en promedio pendientes superiores al 35% (^{Mosquera y col., 2015}) y flujo turbulento. Estas características permiten la aplicación del método de dilución salina en la zona de estudio. Además, según ^{Kite (1993)}, esta técnica debe aplicarse cuando la descarga es inferior a 15 m ³ /s. En la zona de estudio, el caudal máximo medido es de 6 m ³ /s en la salida (M9). Por lo tanto, el método se aplicó para medir la descarga baja, media y alta.

El método específico utilizado fue la inyección instantánea (^{Rantz, 1982}). ^{Frederick y Cobb (1985)}, ^{Kite (1993)} y ^{Bronge y Openshaw (1996)} describen el procedimiento detallado para la medición en campo, y se puede resumir en cuatro pasos: 1) diluir una cantidad de sal conocida en un recipiente de agua, 2) inyectar la solución aguas arriba en un punto en el que el flujo es turbulento, 3) medir la Conductividad Eléctrica (CE) inicial en el área de medición y luego en cada paso de tiempo (el paso de tiempo para el presente estudio fue de 1 segundo), 4) realizar medidas continuas hasta que la CE alcance el valor inicial (±2µS/cm). Las mediciones de descarga son muy precisas cuando las relaciones inicial-máxima de las conductividades eléctricas están entre 2,5 y 3 (^{Bronge y Openshaw, 1996}; ^{Comina y col., 2013}).

Para calcular la descarga, hay que construir la curva tiempo-CE. El área bajo la curva corresponde al aumento de la CE debido a la sal inyectada. El equivalente de sal que atraviesa la sección en cada paso de tiempo se obtiene entonces mediante el factor de conversión (K). En este caso, K = 2,0832 (l/mg ∗ µS/cm). El área bajo la curva se determina mediante la Ecuación 4, y la descarga mediante la Ecuación 5. Donde A es el área bajo la curva de medición (µS/cm∗s); EC(t) es la conductividad eléctrica en el tiempo t (µS/cm); ECb(t) es la conductividad eléctrica inicial del río (µS/cm); M es la cantidad de sal que se inyecta (mg); K es el factor de conversión; y Q es la descarga estimada (l/s).

Para asegurarse de que la solución salina que se inyecta al río se mezcla correctamente, es necesario considerar una distancia adecuada entre el punto de inyección y el área de medición. Aunque existen varias ecuaciones para calcular esta longitud de mezcla (^{Kite, 1993}; ^{Comina y col., 2013}; ^{Comina y col., 2014}), es mejor determinarla en campo para cada sitio (^{Tazioli, 2011}). Como regla general, esta longitud debe estar entre 20 y 70 metros, dependiendo de la descarga y las condiciones del flujo en el área de medición (^{Sappa, Ferranti y Pecchia, 2015}). Además, el tramo entre el punto de inyección y el área de medición debe ser recta y sin encharcamientos para que la sal no se separe del flujo principal (^{Hudson y Fraser, 2002}). Debido a que cada corriente de las 9 microcuencas tiene diferentes propiedades fluviomorfológicas, se utilizaron diferentes relaciones de cantidad de sal-descarga para la medición del flujo. La Tabla 1 muestra una guía para la medición de caudales en el ecosistema de páramo con el método de dilución de sal, basado en la relación de CE inicial y máxima (µ_max/µ0) que debe estar entre 2,5 y 3 para una adecuada medición de caudales (^{Comina y col., 2013}).

Las longitudes determinadas para las diferentes corrientes del área de estudio se encuentran entre 13 y 50 m. Salvo en las condiciones de bajo caudal, las longitudes se encontraban en el rango de 20 - 70 m, tal y como sugieren (^{Sappa, Ferranti y Pecchia, 2015}). Aunque los valores mostrados en la Tabla 1 pueden servir de referencia para calibrar caudales en cuencas con condiciones similares, hay que tener en cuenta que la cantidad de sal a diluir y la longitud de mezcla dependen de la velocidad y turbulencia del flujo, de la CE inicial y de las condiciones de pendiente y encharcamiento del agua en el arroyo.

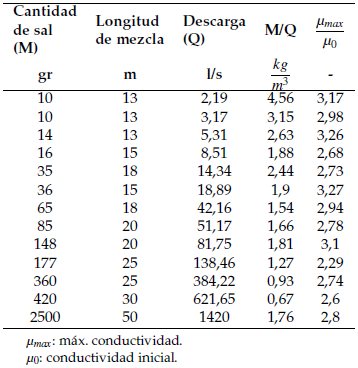
Tabla 1.  Relación entre la cantidad de sal, la longitud de mezcla y la descarga para la medición de caudales por el método de dilución salina en la cuenca estudiada. 

Para el total de ensayos realizados de medición del caudal, la relación media fue de 2,01 kg de sal por m3, con un mínimo de 0,67kg/m ³ y un máximo de 4,56kg/m ³. Estas relaciones coinciden con ^{Valdes (2007)}, quién recomendó valores entre 2 a 5 kg/m ³. Por otro lado, (^{Hudson y Fraser, 2002}) demostraron que la cantidad de sal no es significativa para la aplicación del método de dilución de sal, y concluyeron que, si se aumenta la cantidad de sal, el área bajo la curva de CE aumentaría proporcionalmente y tendría un impacto mínimo en las estimaciones de descarga. No obstante, sugieren utilizar concentraciones de 2kg/m ³.

3.2 Calibración del coeficiente de descarga

Para calcular la curva de descarga de cada vertedero, se determinó el mejor método de calibración para las diferentes condiciones de campo. Para los caudales bajos, se consideró como referencia el método volumétrico por la alta precisión que tiene para estas condiciones. Para los caudales medios y altos, se consideró como referencia el método de dilución salina porque es muy preciso en ríos de montaña (^{Kite, 1993}) y su precisión es superior al 95% en condiciones de mezcla completa (^{Moore, 2004}). Para asegurarse de que los resultados del presente estudio son significativos y para calcularlas diferencias relativas entre los tres métodos descritos, se midió la descarga utilizando todos ellossimultáneamente.

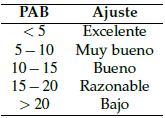
Una vez calculadas las curvas de descarga, se pueden determinar los Coeficientes de Descarga (CD) para cada vertedero. Los CD se calcularon mediante el método de ajuste de mínimos cuadrados (^{World Bank y Government of the Netherlands funded, 1999}), utilizando la relación altura de aguadescarga para cada vertedero y manteniendo constantes los exponentes de las ecuaciones (Ecuaciones 1 a 3). Para obtener la curva de descarga mejor ajustada a los puntos de calibración, se utilizó el Porcentaje de Sesgo Absoluto (PAB) (Ecuación 6) como índice estadístico para evaluar la diferencia entre las observaciones (medición) y la curva de descarga calibrada. Donde X son los datos ajustados; Y son los datos observados; y hX,Yi es la mitad de la media de la suma X +Y. Los criterios para categorizar los resultados se adoptaron de ^{Tokay, Bashor y McDowell (2010)}, que se muestran en la Tabla 2.

Tabla 2.  Criterios para el índice de sesgo absoluto porcentual (PAB). 

4.1 Comparación entre los métodos de medición de caudales

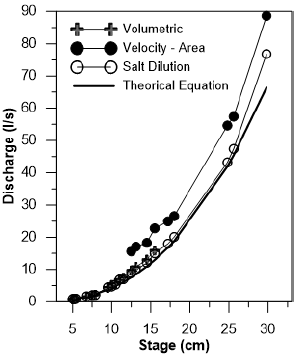
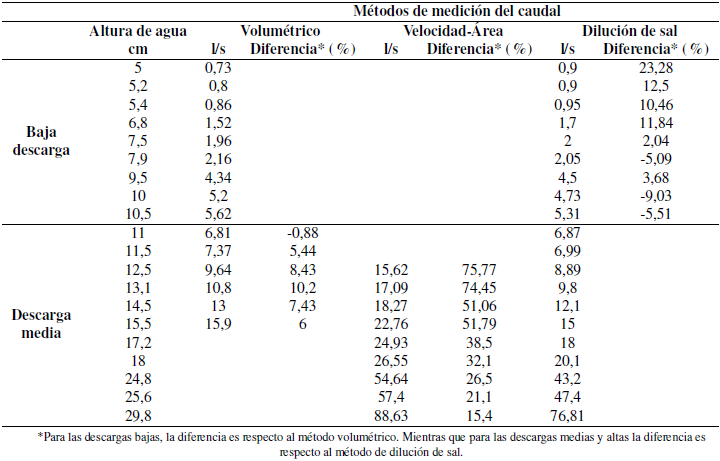
En condiciones de bajo caudal, el método de dilución salina sobrestima ligeramente los valores en comparación con el método volumétrico (0,14 l/s) (la Figura 3 y la Tabla 3 muestran las diferencias entre los tres métodos de medición para 9 microcuencas). Esta sobreestimación podría deberse al hecho de que para condiciones de baja descarga la solución salina no se mezcla completamente en la corriente, siendo la principal condición para una medición eficiente, causando así este error. A medida que aumentan los valores de caudal, también aumenta la turbulencia y la diferencia entre los métodos de dilución salina y volumétrico disminuye hasta un punto en el que el método volumétrico arroja valores más altos para condiciones de caudal medio. Esto se debe a que la precisión del método volumétrico disminuye para una mayor descarga, es decir, el envase se llena de agua mucho más rápido y el tiempo de registro es más corto (< 2 segundos), lo que impide medir con precisión y generan errores de medición.

Figura 3.  Relación etapa-descarga utilizando los tres métodos de medición, promedio de 9 cuencas. 

El método de velocidad-área sobreestima la descarga un 40% en promedio con respecto al método de dilución salina (Figura 3 y Tabla 3). Esto podría deberse al hecho de que los cauces aforados no cumplen las condiciones recomendadas por la Organización Meteorológica Mundial (^{WMO, 1994}), en especial debido a que las líneas de flujo deben ser paralelas a lo largo de la sección del arroyo y que la altura de agua mínima por encima del vertedero debe ser de 15 cm. Estos resultados son similares a los presentados por ^{Gees (1990)} y ^{Tazioli (2011)}; quienes encontraron diferencias de hasta 38% y 50% respectivamente para condiciones de baja y media descarga. Por otro lado, ^{Sappa, Ferranti y Pecchia (2015)} concluyeron que los métodos de dilución salina y de velocidad-área son similares, con pequeñas diferencias entre el 1% y el 8%. Sin embargo, las diferencias con la presente investigación radican en que en ese estudio se utilizaron canales con flujo laminar para la medición del correntómetro.

Tabla 3.  Diferencias entre los tres métodos de medición de caudales. 

A partir de estos resultados, se construyó la curva de descarga para los diferentes vertederos, considerando los datos del método volumétrico para condiciones de baja descarga (Q < 5,5 l/s) y del método de dilución salina para condiciones de media (5,5 ≤ Q < 67,5 l/s) y alta descarga (Q ≥ 67,5 l/s).

4.2 Calibración de los coeficientes de descarga

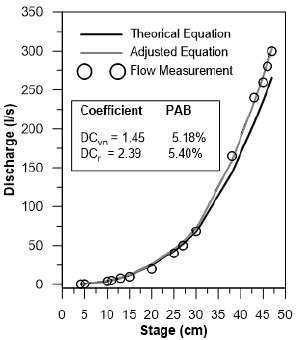
La Tabla 4 muestra los coeficientes de descarga calibrados para los 9 vertederos; hubo 5 DCr que no se calibraron porque no había suficientes datos de medición de caudales sobre la descarga alta en estos vertederos. El error de ajuste de los valores de descarga aforados comparado con la curva de descarga calibrada son bajos (PAB ≤ 5% en la Tabla 4). Por otro lado, los DCvn varían entre 1,19 y 1,56 para la sección triangular (DCvn teórico= 1,37), y entre 1,53 y 3,00 para la sección rectangular (DCr teórico= 1,77). Estas diferencias representan un error relativo de hasta el 15% para vertederos con sección en V (DCvn) y de hasta el 41,0% para la sección de vertedero rectangular (DCr) en comparación con los valores teóricos (Tabla 4). Las diferencias entre los coeficientes teóricos y los calibrados se deben a las características específicas de cada río y caudal, como la construcción de la estructura, la pendiente del cauce del río y la sección transversal.

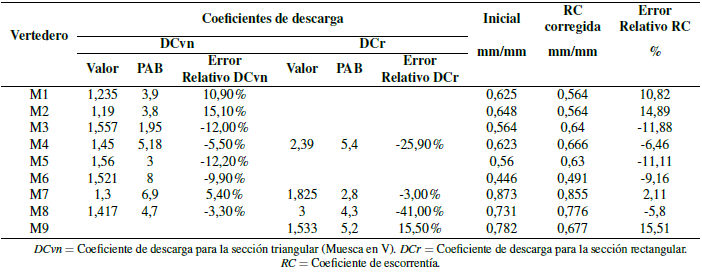
Tabla 4.  Coeficientes de descarga calibrados para las ecuaciones de descarga y su efecto en los coeficientes de escorrentía (RC) de cada microcuenca. 

Con las curvas de descarga calibradas se obtuvo un hidrograma más preciso. Esto permite determinar el error en el rendimiento hídrico de cada microcuenca cuando se utilizan las ecuaciones teóricas con los coeficientes no calibrados. El coeficiente de escorrentía (CR = precipitación de entrada/escorrentía de salida) representa el rendimiento hídrico de una cuenca. El error relativo en el CR se sitúa entre el 2,11% y el 15,51% con un sesgo tanto negativo como positivo encontrado entre este grupo de vertederos, 6,56% en promedio para todas las microcuencas (Tabla 4). Como se observa, cuando los vertederos no están calibrados, el cálculo del balance hídrico de las microcuencas se ve afectado.

Se realizó un análisis de sensibilidad de los coeficientes de descarga en el hidrograma. En primer lugar, se determinó la descarga anual acumulada cambiando sólo el DCvn ajustado en la Ecuación 3; luego, se hizo la misma estimación utilizando sólo el DCr calibrado (DCvn= coeficiente teórico). Según estos análisis, para un año hidrológico, la DCvn afecta 4 veces más las descargas bajas y medias que la DCr a las altas. La estimación del caudal es más sensible a DCvn porque en la mayor parte del tiempo (95% del total de registros) el caudal es inferior a 65,5 l/s (h < 30 cm en este estudio); es decir, el caudal pasa sólo por la sección triangular de los vertederos. Además, la ecuación teórica para la sección triangular sólo es válida para un caudal superior a 1,41 l/s (h = 6,4 cm) (^{United States Bureau of Reclamation, 2001}), que es mayor a los caudales bajos observados para la zona de estudio (0,70 l/s; h = 5 cm), especialmente en condiciones secas.

Figura 4.  Calibración de la curva de descarga para el vertedero compuesto M4.