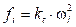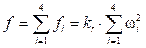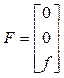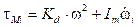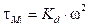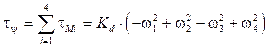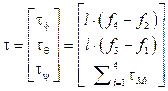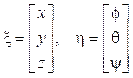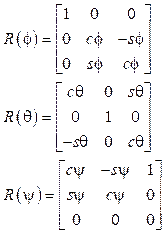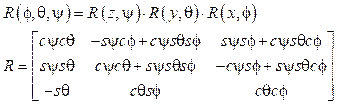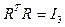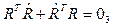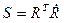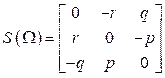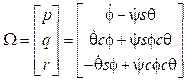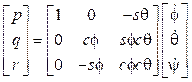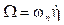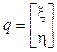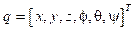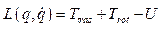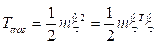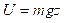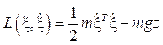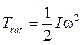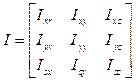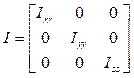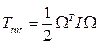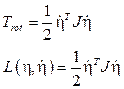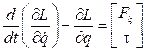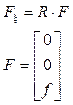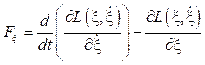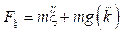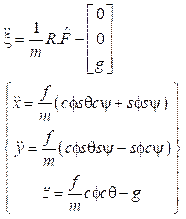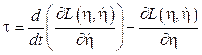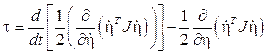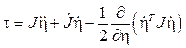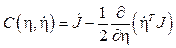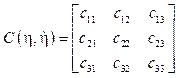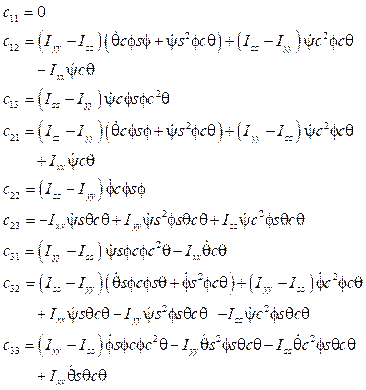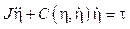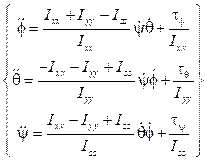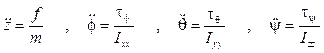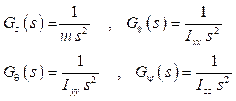I. Introducción
Debido a los diferentes factores que se presentan en los cultivos de café y cacao, se desea tener control e inspección a través del desarrollo de tecnologías que permitan el mejor crecimiento y entorno productivo de estos cultivos. Una de estas innovaciones es el uso de los vehículos aéreos no tripulados, también llamado VANT o UAV por sus siglas en inglés; estos son aeronaves piloteadas mediante control remoto o por controladores autónomos incorporados en la misma estructura 1 es decir, es una tecnología conformada por tres agentes principales: una plataforma aérea, un enlace de datos entre tierra y aeronave, y una estación de control en tierra 2. Estas permiten monitorear grandes áreas de campo en tiempo real, así como la detección de plagas y fallas en los cultivos, además se reducen los costos en comparación con vuelos tripulados, y las imágenes captadas por el VANT no presentan problemas con las nubes en comparación con las imágenes por satélite.
Al depender de su configuración los VANT pueden ser los que utilizan rotores (uno, dos, tres o múltiples rotores) o los que utilizan alas flexibles 3. Dentro de los que utilizan rotores se encuentra el VANT a cuatro motores llamado quadrotor, el cual se representa de forma esquemática y es objeto de estudio del presente, considerado como una estructura en forma de cruz con su centro de gravedad en concordancia con el centro de masa y los cuatro motores en la punta de cada brazo 4. Para el modelamiento del mismo existen dos métodos de aproximación; para el presente se escogió la formulación matemática de Euler-Lagrange para hallar las ecuaciones que permiten caracterizar el comportamiento del quadrotor validado mediante software computacional. El modelamiento de un VANT es definido principalmente por la cinemática y la dinámica del sistema. En la dinámica se incluyen los momentos de inercia, los cuales son los encargados de describir la dinámica rotacional de la aeronave, para ello existen diferentes técnicas matemáticas para hallarlo, o también se suelen usar programas de diseño mecánico que las calculan automáticamente. Uno de esos programas es Solidworks, que es un software de entorno CAD para diseño de mecanismos y estructuras muy ampliamente usado en la ingeniería, el cual para el presente proyecto se usó para estimar los momentos de inercia del quadrotor ensamblándolo con el menor número de partes posibles.
En el mercado existen una gran variedad de programas de simulación para poner a prueba el diseño de una estructura, pero en concreto uno de los más usados en la ingeniería es Simulink, un entorno de simulación integrado a Matlab que ofrece una amplia gama de herramientas para simular casi cualquier sistema mediante diagramas de bloques. Dentro de las tantas herramientas que posee Simulink se encuentra Simscape Multibody, el cual utiliza diseños de mecanismos en formato CAD para simular el movimiento de estructuras mecánicas a través de las propiedades físicas que estas poseen.
Para implementación y pruebas de controladores se suelen usar con gran frecuencia los VANT, a continuación, se muestran algunos proyectos en donde se modela y simula quadrotores al probar en ellos algunas estrategias de control. La estrategia de control más conocida y usada es el PID, y en particular un PID independiente para el eje de orientación del VANT al utilizar una placa Arduino uno 1. Se describe en la literatura el paso a paso de cómo se diseñan las diferentes partes de un sistema de esta naturaleza y se presenta con frecuencia cómo se modela en Simulink, bloque por bloque; se utilizan con frecuencia VANT comerciales, como el Draganflyer SAVS. La placa de control a parte del controlador, también posee una IMU de tecnología MEMS que trae integrado en su tarjeta el giróscopo y el acelerómetro que además ayuda a mitigar un poco las perturbaciones provocadas por el efecto Coriolis. Durante las pruebas se presenta la necesidad de corregir algunos parámetros como el filtro de Kalman; también de la IMU en cuanto a los ángulos de orientación y del controlador cuyo ajuste de ganancias se hizo de forma manual para que tuviera una respuesta estable y un vuelo estático ante perturbaciones externas.
Una forma común de afrontar el problema de los VANT es construirlo desde cero, i.e., diseñar y construir un cuadricóptero a control remoto al tener en cuenta para el diseño mecánico la ligereza, la rigidez, la resistencia y aerodinámica montado en SolidWorks. Para el diseño del modelo dinámico del VANT se aplicaron las fórmulas de Lagrange-Euler con lo que se obtuvo las ecuaciones que describen el comportamiento del VANT. Con la planta ya establecida se implementa un controlador PID como estrategia de control y un filtro complementario para obtener las lecturas de los sensores acelerómetro y giróscopo. De esta forma, se determinan los ángulos de cabeceo y alabeo, lo que entregó como resultados una respuesta satisfactoria. Sin embargo, se hace necesario ajustar las constantes del controlador para que el sistema sea estable ante cualquier tipo de perturbación 5.
Diversas estrategias de controladores PID de lazo cerrado doble se utilizan con frecuencia, lo cual divide el sistema en dos partes, un control de lazo interior para la orientación y un control de lazo exterior para la posición; se aplicó a un VANT de referencia MAV que es un quadrotor de pequeñas proporciones. El modelo dinámico se obtiene mediante el uso de las ecuaciones de Newton-Euler. El controlador PID se implementa en la planta y las pruebas se hacen mediante Simulink. Los resultados de la simulación se presentan de forma tal, que varias señales de escalón se aplican como una referencia para los tres ángulos y para la altura. Los resultados mostraron que los controladores tienen una importante habilidad adaptativa y robustez. Se concluye, que el sistema de un lazo cerrado solo puede manejar cuatro señales de control y el de doble lazo cerrado seis(6) señales de control, por lo que el quadrotor logra alcanzar el punto de referencia 6.
II. Resultados
Se describe el modelado matemático del quadrotor que dispone el grupo de investigación en Control Avanzado -GICAV de las Unidades tecnológicas de Santander-UTS, mediante el cual se caracterizó la planta con la que se trabajó. Debido a que el modelo dinámico del VANT ya ha sido analizado al usar el método de Newton-Euler 7, dicho modelo se decidió desarrollar mediante la formulación matemática de Euler-Lagrange.
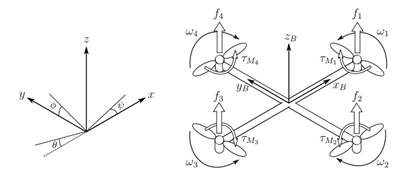
Para poder comprender cómo es posible cada uno de los movimientos que realiza el quadrotor, primero se debe realizar un análisis detallado de cómo el VANT lo logra físicamente. Para ello se tiene el siguiente diagrama de fuerzas y marcos de referencia que se expone en la Fig 1. De todas las ilustraciones presentes en la literatura, se usa esta, debido a que en ella se puede apreciar de gran forma la descripción general del quadrotor, mismo que es caracterizado por los sistemas de coordenadas, las fuerzas, momentos, y velocidades angulares que generan los cuatro motores.
Existen dos tipos de estructuras de acuerdo al marco de referencia fijo al quadrotor: una en forma de cruz y la otra en forma de X. La estructura elegida para el modelamiento del mismo es la de tipo cruz, donde los actuadores que son los motores, se encuentran en las puntas de cada brazo y los ejes de coordenadas coinciden con los brazos de la estructura 4.
De acuerdo con la Fig 1. en el modelo se define a x B , y B y z B , como el sistema de coordenadas fijo al VANT, donde x B es el eje de dirección normal de ataque del quadrotor, es decir, la dirección en la que el vehículo avanza hacia adelante, z B es el eje vertical orientado en sentido ascendente y y B es el eje perpendicular a x B y z B positivo que cumple con la ley de la mano derecha (sistema dextrógiro). El sistema de coordenadas inercial está descrito por los ejes x y z que se consideran fijos con respecto la tierra 8.
El empuje aerodinámico se genera debido a la rotación de las hélices en un fluido viscoso, aire en este caso, y es utilizado para poder elevar el VANT y mantenerlo en el aire 1. El empuje se relaciona con la velocidad de rotación de los motores mediante la siguiente expresión, donde k t es la constante de empuje y la velocidad angular del motor i es denotada por ω i :
Si se considera que los motores están perfectamente alineados con respecto al sistema de coordenadas móvil, la dirección de la fuerza de empuje será en el eje z del sistema de referencia mencionado, donde esta componente en el resto de ejes es nula 1. El empuje total del quadrotor el cual hará que este se desplace verticalmente, será la suma del empuje de todos los motores tal como se ve en (2), y en (3) se define el vector de fuerza traslacional del VANT F debido a al empuje total f expresada solo en la dirección del eje z 8:
El momento debido al arrastre aerodinámico, es el que se encarga de girar el quadrotor alrededor de su propio eje para cambiar su sentido de orientación. Este se genera en el eje z del cuerpo por la diferencia de velocidad de giro de los rotores, debido a la fricción entre el aire y las hélices de los rotores. Al girar las hélices, estas se ven sometidas a un esfuerzo causado por el rozamiento que se produce entre dichas hélices en movimiento y el aire, lo que genera un momento o torque en sentido contrario a la dirección de giro de los rotores 1. Para entender cómo se produce este fenómeno, en la siguiente expresión se define el torque generado en el rotor:
donde K
d
es la constante de arrastre e I
m
es la inercia del motor. El termino 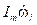 normalmente es despreciado debido a que el efecto
normalmente es despreciado debido a que el efecto 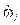 es muy pequeño 9. El coeficiente K
d
posee un valor mayor a cero y depende entre otros factores, de la densidad del aire, del radio y de la forma de la hélice 3. Por lo tanto, el momento o torque aerodinámico del motor es:
es muy pequeño 9. El coeficiente K
d
posee un valor mayor a cero y depende entre otros factores, de la densidad del aire, del radio y de la forma de la hélice 3. Por lo tanto, el momento o torque aerodinámico del motor es:
El momento total es proporcional al empuje que genera cada rotor y es generado por el desequilibrio del conjunto de fuerzas f2 y f4 con f1 y f38. Este movimiento es posible ya que los rotores pares 2 y 4 giran en sentido de las agujas del reloj, y los rotores impares 1 y 3 lo hacen en sentido opuesto 1. Por esta razón el momento debido al arrastre aerodinámico es denotado con τψ:
Los momentos correspondientes en la dirección de los ángulos del marco del cuerpo mencionados anteriormente, se denotan con el vector τ mediante la siguiente expresión, donde l es la distancia entre el rotor y el centro de masa del quadrotor:
Se designa el vector ξ para las coordenadas traslacionales o posición lineal absoluta, y el vector η para las coordenadas rotacionales o posición angular que representa los ángulos de Euler: roll φ, pitch θ y yaw ψ.
Para describir la orientación del VANT se usan los ángulos de Euler y más específicamente la convención XYZ o también llamada ángulos de Tait-Bryan; el uso de estos ángulos se ve muy extendido 1 a causa de que numerosas organizaciones, han publicado diversos estándares para ser seguidos debido a la especial importancia de las convenciones internacionales en vehículos aéreos, y remarca la norma DIN 9300 adoptada por la ISO 1151-2:1985 como uno de esos estándares.
A continuación, en (9) se muestran las matrices que representan la orientación de un sólido en el espacio, esta son llamadas matrices básicas de rotación de un sistema espacial de tres dimensiones 10, donde cφ = cos (φ) y sφ = sin (φ):
En la ecuación (10) se obtiene la matriz de rotación completa del marco de referencia del cuerpo con respecto al marco de referencia fijo conocida como matriz de coseno directa:
Las matrices ortogonales aparte de la propiedad mencionada, poseen una propiedad con los determinantes, la cual es que estas poseen determinantes de ±1. Tal es el caso de la matriz de coseno directa que es considerada como una matriz ortogonal propia, donde su determinante es +1, si fuera impropia tendría un determinante de -1 11. Estas matrices también poseen otras propiedades que pueden determinar la cinemática rotacional del VANT, como la que se muestra a continuación:
donde I 3 representa una matriz identidad de 3x3 y R es la matriz de rotación. La anterior ecuación representa la propiedad más conocida de las matrices ortogonales y esta se deriva con respecto al tiempo para obtener la siguiente expresión 12:
Se define a:
Se puede apreciar que S es una matriz anti simétrica, es decir que si A es una matriz cuadrada, esta es anti-simétrica si A T = -A. Por lo tanto, existe una propiedad que relaciona la derivada de las matrices ortogonales con las matrices anti simétricas 12. Al realizar la operación mostrada en la ecuación (13), se le puede asignar a la matriz anti simétrica S los siguientes términos:
A S(Ω) por los términos que contiene se la conoce como el tensor anti simétrico de velocidad angular 11. Que son las componentes del vector de velocidad angular del VANT cuyos valores son:
Ya conocidos los valores del vector Ω en términos de
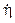 , se calcula la matriz de transformación ω
n
que permitirá obtener la relación entre las velocidades angulares para separarlas matricialmente:
, se calcula la matriz de transformación ω
n
que permitirá obtener la relación entre las velocidades angulares para separarlas matricialmente:
A continuación, se presenta la dinámica del quadrotor planteado mediante la formulación de Euler-Lagrange, la cual está basada en el concepto de energía mecánica (energía cinética y potencial) 8. Esta formulación describe el movimiento traslacional y rotacional en un sistema de seis grados de libertad, al utilizar el vector de coordenadas generalizadas q13:
donde el vector ξ contiene las coordenadas traslacionales del centro de masa del VANT con respecto al marco inercial (x, y, z) y el vector η contiene las coordenadas rotacionales para la orientación del vehículo que son los ángulos de Tait-Bryan (φ, θ, ψ) 3. Estos dos vectores fueron vistos en (8) de forma que el vector q queda de la siguiente forma:
El Lagrangiano se obtiene al modelar la energía del sistema, definido como la diferencia entre la energía cinética y la energía potencial, donde la energía cinética del sistema es determinada por los movimientos traslacionales y rotacionales. Mientras la energía potencial se relaciona únicamente por la altura del quadrotor 13. De lo anteriormente dicho se define el Lagrangiano como una función del vector de coordenadas generalizadas y su primera derivada con respecto al tiempo de la siguiente forma:
Se tiene la expresión para desarrollar la energía cinética traslacional:
En seguida se describe la energía potencial, la cual como se mencionó anteriormente solo está presente en el eje z de las coordenadas traslacionales y está dada por:
donde m es la masa del quadrotor, g es la aceleración gravitacional y z es la altura del vehículo. En conclusión, el Lagrangiano en términos de las coordenadas de traslación es:
La energía cinética rotacional del cuerpo rígido es:
Ya que un mismo cuerpo que posee diferentes ejes de rotación, pueden tener diferentes momentos de inercia en torno a esos ejes, entonces es conveniente el uso de una matriz o tensor de inercia para resumir todos esos momentos de inercia de un cuerpo en una sola cantidad 14. De esta forma el tensor de inercia se define como:
Se asume que el quadrotor posee una estructura simétrica con los cuatro brazos alineados con los ejes x, y del cuerpo 9. Por lo tanto, se define el tensor de inercia del cuerpo rígido como una matriz diagonal cuyos componentes se conocen como los principales momentos de inercia 15:
La energía cinética rotacional del sistema es:
Finalmente, la energía cinética rotacional queda expresada en la siguiente ecuación, donde además ésta también define el Lagrangiano para los términos de las coordenadas rotacionales del quadrotor:
El modelo dinámico completo del quadrotor es obtenido de las ecuaciones de Euler-Lagrange con las fuerzas generalizadas externas 3 mediante la siguiente expresión:
donde τ representa los momentos de roll, pitch y yaw como los pares resultantes del movimiento rotacional y F
ξ representa la fuerza resultante del movimiento traslacional, la cual se desarrolla a partir del vector de fuerza traslacional 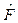 como se muestra en la siguiente expresión donde R es la matriz de coseno directa:
como se muestra en la siguiente expresión donde R es la matriz de coseno directa:
En la siguiente expresión se desarrolla las ecuaciones de Euler-Lagrange para las coordenadas de traslación:
Al reescribir la ecuación anterior en función del vector de estado ξ 8, hace posible despejar las aceleraciones lineales del sistema:
Las ecuaciones de Euler-Lagrange para el movimiento rotacional son:
O también se pueden escribir de la siguiente forma:
Al derivar con respecto al tiempo a la expresión en paréntesis se obtiene la siguiente ecuación:
Donde se define a la matriz de Coriolis como:
Cuyos valores son:
Al reescribir la ecuación de Euler-Lagrange en términos de las coordenadas rotacionales:
En la ecuación anterior se obtuvieron las expresiones no lineales del sistema, las cuales son muy complejas, y para hacer el respectivo despeje de cada una de las aceleraciones angulares se tendrá en cuenta el procedimiento usado en algunas referencias 16, 17, 18. Dicha aproximación hace mención a considerar el ángulo pequeño, lo cual consiste en que el sistema considerado está en un punto de equilibrio, donde los ángulos de Euler tienden a cero.
Después de aplicar los despejes mencionados se define la dinámica de rotación en (40). El resultado obtenido es distinto a gran parte de la literatura consultada 17:
Sin embargo, la expresión anterior puede ser más reducida, pues cuando se considera que el VANT está en equilibrio, no solo los ángulos de Euler tienden a cero sino también sus velocidades angulares. Al tener en cuenta estas consideraciones, el modelo dinámico original del quadrotor en términos de los movimientos traslacionales y rotacionales pueden ser simplificado, donde se obtiene las siguientes expresiones lineales 18:
Para finalizar, se procede a obtener la función de transferencia del sistema que permitirá comprender la naturaleza y obtener la respuesta transitoria para posterior control, al aplicar la transformada de Laplace a los términos de (41):
A continuación, se presentan los resultados obtenidos de la simulación del quadrotor, el cual incluye el control de posición y orientación del VANT ante distintos tipos de perturbaciones o disturbios. Los resultados se obtendrán a partir de dos simulaciones diferentes, una sin perturbación y la otra con perturbación. Los datos obtenidos se visualizarán a través de la herramienta Data Inspector y el resultado se complementará en el visualizador de Simscape Multibody con la animación del movimiento. Esto servirá para probar la estabilidad del quadrotor mientras esta en vuelo a una altura determinada.
Simulación del sistema sin perturbación
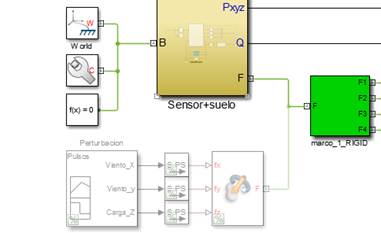
Para la simulación del vuelo sin perturbaciones inicialmente fue necesario inhabilitar los bloques correspondientes que generan las señales de perturbación, los cuales se muestran en la Fig 2. Esto se hace con el fin de poder observar la estabilidad del sistema en un ambiente de vuelo ideal.
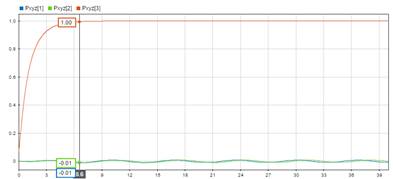
El tiempo establecido para la simulación fue de 40 segundos, lo necesario para que el quadrotor alcance la altura deseada y así poder analizar su comportamiento en ese estado. Las referencias o valores deseados fue el de alcanzar un metro de altura y mantener el vehículo en esa posición sin ningún tipo de desplazamiento adicional. Al correr la simulación, en las Fig 4., Fig 5., y Fig 6., se presentan los resultados obtenidos de la posición y orientación del VANT visualizados por medio del Data Inspector, donde las convenciones P xyz 1, P xyz 2, y P xyz 3 se refieren en este orden a las posiciones P x , P y y P z . Y las convenciones Euler1, Euler 2, y Euler 3 se refieren en este orden a los ángulos de Euler yaw, pitch y roll. En la Fig 3. se puede observar una captura del vuelo del quadrotor a través del visualizador de Simscape Multibody.
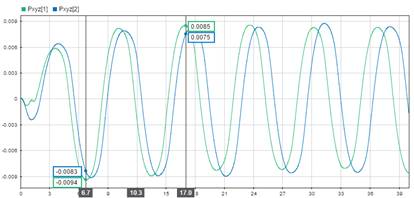
En la Fig 4., P xyz 3 simboliza la gráfica de altura y se observa que el sistema alcanza el valor deseado a los 6.6s sin presentar oscilaciones ni sobrepasos manteniéndose estable, mientras que los otros valores que representan el desplazamiento horizontal mantienen su estado inicial, pero con un poco de oscilación debido a la acción de control del compensador proporcional que se agregó a las referencias de los controladores de pitch y roll. A pesar de dichas oscilaciones como se puede apreciar en la Fig 5. el cual representa mejor estas respuestas, el VANT se mantiene estable, ya que estos valores solo oscilan entre 0.0085 y -0.0094 metros de la referencia deseada, lo suficientemente bajo como para ser despreciado y no desestabilizar el sistema.
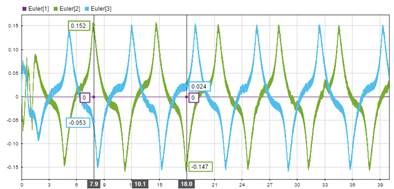
En la Fig 6. se muestran los resultados obtenidos de la simulación para la orientación del VANT, los cuales son representados por los ángulos de Euler. Como se puede apreciar, presenta leves oscilaciones menores a un grado en los ángulos de pitch y roll etiquetadas respectivamente por Euler2 y Euler 3. Aunque el controlador de estos ángulos es un tipo PID, la referencia de estos es constantemente alterada por la acción de control del compensador proporcional para los ejes x e y. En el ángulo de yaw representado por la línea morada no presenta oscilaciones muy apreciables, debido a que la referencia de esta es un valor constante y no una acción de control.
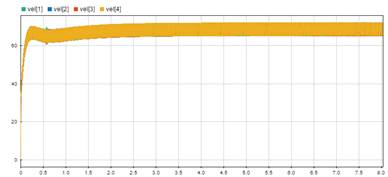
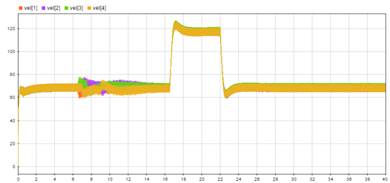
Para corroborar los resultados mostrados, en la Fig 7. se muestran las gráficas de velocidad que se sensaron a las propelas del quadrotor durante los primeros 8s de simulación. Dichas gráficas representan los distintos cambios de velocidad que tuvieron que hacer las hélices para controlar el ascenso y estabilidad de vuelo del VANT. Como se puede observar durante los primeros dos segundos hubo un sobre paso en la velocidad producto del despegue de la aeronave y en el resto del tiempo de simulación las velocidades de las propelas se mantuvieron al variar en un rango constante para permanecer el vehículo en la posición de referencia.
Con los datos obtenidos se puede concluir que el vuelo del VANT sin perturbación fue estable, ya que mantiene la posición inicial que se escogió con un margen de error muy pequeño.
Simulación del sistema con perturbación
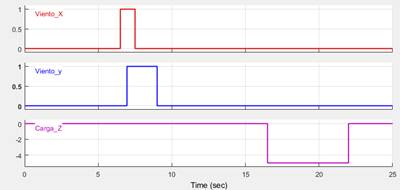
Para la simulación con perturbación, se habilitaron los bloques de fuerza externa y de perturbación vistos en la Fig 2., el cual por medio de este último introduce al bloque de fuerza externa señales tipo pulso de tiempo variable como los que se muestran en la Fig 8., que hará que genere fuerzas en los tres ejes de posición lo cual provoca un desplazamiento brusco que desestabilice el VANT de su posición de referencia. De esta forma el quadrotor debe ser capaz de regresar a dicha posición una vez haya acabado la perturbación.
Las señales de perturbación se aplicaron de la siguiente forma: A los 6.5 s y 7s se añaden fuerzas de 1N a los ejes de posición horizontal para simular una corriente de aire, primero con un tiempo de duración de 1s para la señal de viento en el eje x y segundo un tiempo de 2s para la señal de viento en el eje y. La otra señal de perturbación es de -5N para la altura la cual se aplica a los 16.5s, esta se usa para simular que al quadrotor se le adiciona en su centro de masa una carga de 500g. La idea es que el VANT sea capaz de regresar a su posición de referencia con esta carga, pues los motores tienen la capacidad de lograrlo, y al quitar la carga este se debe mantener o regresar a esa posición.
Al correr la simulación, en las Fig 8., y Fig 9. se tienen los resultados de la posición y orientación del quadrotor, y en la Fig 10. se tiene la gráfica que representa las velocidades de las hélices, estas tres obtenidas a través del Data Inspector de Simulink al aplicarles las señales de perturbación.
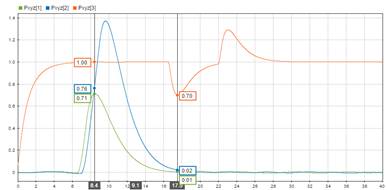
Como se pudo observar en las gráficas mencionadas, los primeros 2s de la simulación se observa un leve sobrepaso en la gráfica de velocidad vista en la Fig 11., producto del despegue de la aeronave al igual que en la simulación sin perturbación. Después de ese tiempo las señales de disturbio se aplicaron en el tiempo establecido lo que provoca en el VANT un máximo desplazamiento a lo largo del eje x de 71cm y a lo largo del eje y de casi 1.4m como se observó en la Fig 8. En la Fig 12. se observa una captura del movimiento a través del visualizador de Simscape Multibody del quadrotor en el instante en que a este se lo somete a las perturbaciones mencionadas.
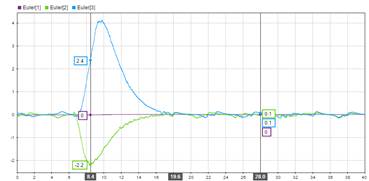
Al quitar estas perturbaciones, el sistema de control provoca un cambio en las velocidades de las hélices como se apreció en la Fig 11. El efecto que produce este cambio genera una inclinación pico en el ángulo de roll de más de 4° y en el ángulo de pitch de -2.2° visto en la Fig 9., lo que hace que el quadrotor se desplace en sentido contrario a la dirección que se había dirigido y regrese a su posición de inicial.
Sin embargo, al momento de llegar a esa posición a los 16.5s se le aplica la otra señal de perturbación, el cual es una carga de 500g que como se ve en la línea anaranjada de la Fig 9., esta carga hace que el VANT descienda hasta 70cm y provoque que el controlador de altura incremente la velocidad de las cuatro hélices como se ve en la Fig 11.; dicho incremento genera una fuerza de empuje que hace ascender al quadrotor hasta su posición de referencia. Después de 22s la carga se elimina y por efecto de la fuerza de empuje que la aeronave tenía, este bruscamente se eleva a más de 1.2m, pero de nuevo el controlador de altura actúa y hace reducir la velocidad de las hélices para disminuir la fuerza de empuje lo que provoca que el VANT regrese a su posición inicial y termine estabilizándose. Después de haber quitado las señales de perturbación, se pueden observar en las gráficas de posición y orientación leves oscilaciones hasta el final de la simulación, igual como se había apreciado en los resultados de la simulación sin perturbación.
III. Conclusiones
Mediante la técnica de aproximación propuesta de Euler-Lagrange se logró obtener las ecuaciones que caracterizan cada uno de los movimientos que realiza el quadrotor dividido en tres grados de libertad traslacionales y tres rotacionales, en la cual a este se le consideró como un cuerpo rígido perfectamente simétrico cuyo origen del sistema de coordenadas está ubicado en el centro de gravedad.
Para obtener la matriz de transformación que permitió definir la cinemática rotacional del sistema, fue necesario calcular la matriz correspondiente al tensor anti simétrico de velocidad angular, la cual permite obtener el valor de la velocidad angular del VANT en función de la velocidad angular del marco inercial, que en la mayoría de las referencias consultadas no se hizo una demostración detallada de la misma, por lo que se decidió acudir a distintos textos relacionados a la robótica y a la mecánica clásica para realizar dicha demostración.
El desplazamiento horizontal del VANT es posible gracias a los ángulos de inclinación provocados por los movimientos de pitch y roll que hace que el vector de fuerza se incline y logre empujar la estructura hacia esa dirección. Para desplazarse en el eje x con respecto al marco inercial se debe efectuar una inclinación del ángulo de pitch la cual se obtiene al rotar en torno al eje y, y para realizar un desplazamiento a lo largo del eje y se debe efectuar una inclinación del ángulo de roll la cual se obtiene al rotar en torno al eje -x.
Al proponer un valor inicial a las velocidades angulares y al implementar la aproximación de ángulo pequeño, la cual plantea que el cos φ ≈ cos θ ≈ cos ψ ≈ 1 y que el sin φ ≈ sin θ ≈ sin ψ ≈ 0 al momento de obtener las expresiones correspondientes a las aceleraciones lineales y angulares del sistema, la cual son funciones no lineales, permitió linealizar dichas expresiones para que de esta forma se pudieran obtener ecuaciones más sencillas para trabajar con ellas y que se lograra implementar una estrategia de control conocida.
A través de los bloques incorporados de la librería de Simscape Multibody y de los controladores diseñados con la herramienta PID tuner de Matlab, se logró una simulación en donde el sistema consiguiera llegar a la posición deseada y que ante distintas perturbaciones generadas que produjeran desplazarlo de dicha posición, este reaccionara y logre retornar a la posición de referencia.
El tensor de inercia es la matriz de momentos de inercia que permite definir la dinámica rotacional del quadrotor, conformada fundamentalmente por los principales momentos de inercia, los cuales son tomados desde el centro de masa del VANT, y por los productos de inercia, los cuales son despreciados al considerar que el centro de masa del quadrotor está ubicado en su centro de gravedad. Por lo tanto, dicho tensor es uno de los agentes más importantes a la hora de probar la estabilidad del sistema, ya que, si no tiene una buena distribución de masas en la estructura, el tensor de inercia puede contener principales momentos de inercia asimétricos y productos de inercia apreciables que generen inclinaciones y por consiguiente la desestabilización del sistema.
Se observó que la base del marco que originalmente tiene el quadrotor al ensamblarla en Solidworks, posee unos momentos de inercia ligeramente asimétricos y mediante las simulaciones realizadas en Simulink, se comprobó que esto produce una inclinación en el VANT lo cual genera un desplazamiento anormal, por lo que la base de dicho marco para la simulación fue cambiado por otro de dimensiones similares que tuviera momentos de inercia simétricos y por lo tanto, se evitó que el quadrotor en cierta posición se desplace de forma indeseada.
Se obtiene un procedimiento de gran interés y por ende un aporte significativo para el estudio de los VANT, como lo es que mediante la aplicación de la dinámica rotacional del mismo y al utilizar Simulink en conjunto con la librería Simscape Multibody y Solidworks, se facilite el diseño de este tipo de estructuras, con las cuales se pueden reducir los tiempos de construcción y la implementación de algoritmos de control para aplicaciones particulares como lo es la agricultura de precisión.