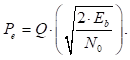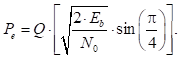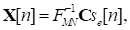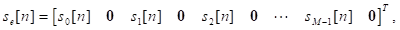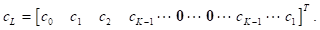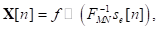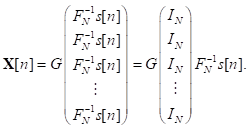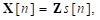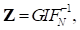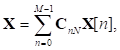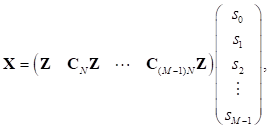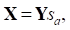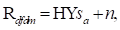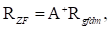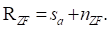Introducción
En los últimos años, ha existido un incremento en los sistemas de comunicaciones móviles y con el avance de la internet y teléfonos inteligentes es evidente que la trasmisión y recepción digital de datos aumente cada día, por lo que es necesario mayores anchos de banda y sistemas más eficientes 1), (2. La futura red inalámbrica 5G requiere mayor eficiencia espectral y baja latencia. En la actualidad el sistema de multiplexación por división de frecuencia generalizado (Generalized Frequency Division Multiplexing, GFDM) tiene una atractiva y significativa atención por los investigadores del área debido a sus propiedades beneficiosas para cumplir con los retos de la próxima generación de la red inalámbrica móvil 3.
Un bloque de símbolo GFDM consiste de M × N muestras donde N es el número de sub-portadoras y M las ranuras de tiempo. Además, utiliza un único Prefijo Cíclico (Cyclic Prefix, CP) para un bloque completo de símbolos GFDM. Comparado con el sistema de Multiplexación por División en Frecuencia Ortogonal (OFDM) que actualmente es utilizado en el núcleo de la capa física de la red inalámbrica 4G que usa un CP para cada símbolo transmitido, GFDM presenta mayor eficiencia espectral 1, 4.
La transmisión de información se realiza al usar modulación por desplazamiento de fase binario (Binary Phase Shift Keying, BPSK) y modulación por desplazamiento de fase en cuadratura (Quadrature Phase-Shift Keying, QPSK) donde cada una se ve afectado por el ruido y el canal en medida diferente 2, (5. En este sentido, el estudio del desempeño de las diferentes técnicas de modulación en el sistema GFDM es un tema importante en el desarrollo de la red inalámbrica 5G3.
La presente investigación tiene la siguiente estructura: la Sección II, revisa las modulaciones digitales BPSK y QPSK, el sistema de transmisión y recepción GFDM y la característica de los canales utilizados. La Sección III proporciona detalles de los parámetros a considerar en las simulaciones de los resultados. Los resultados de la simulación se presentan en la Sección IV para examinar y analizar el desempeño de los diferentes esquemas de modulación. La Sección V se concluye la investigación.
Técnicas de modulación digital, sistema GFDM y canales de comunicación
A. Modulación por Desplazamiento de Fase Binaria
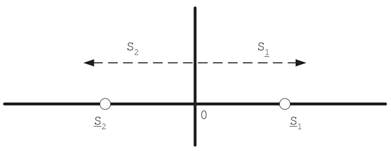
La modulación por desplazamiento de fase (Phase Shift Keying, PSK) es un esquema de modulación digital que implica el envío de mensajes al cambiar la fase de la señal de referencia o señal de portadora 6. En la modulación BPSK, la información que se transmite a través de un canal de comunicación se envía durante la fase de la portadora, una fase particular de 180° se usa para representar la información discreta 2. La Fig 1. representa la región de decisión y constelación de la señal BPSK. La probabilidad de error es dada por (1).
B. Modulación por Desplazamiento de Fase en Cuadratura
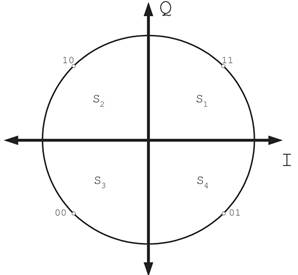
QPSK implica el uso de cuatro fases. En general, estas fases son equidistantes entre sí. El diagrama de la constelación y la región de decisión se ilustran en la Fig 2..
La tasa de bits de la modulación QPSK es el doble de la modulación BPSK, lo que representa un uso más eficiente del espectro (2), (6). La probabilidad de error está dada por (2).
C. Sistema GFDM
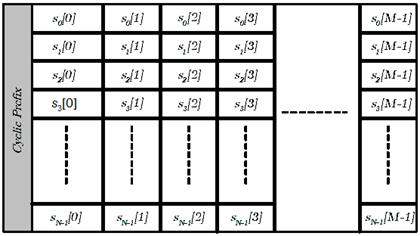
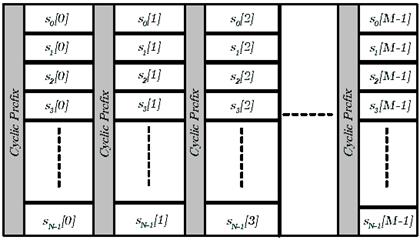
GFDM es un sistema que utiliza un CP para la transmisión de los bloques de símbolos GFDM que proporciona una ecualización de baja complexidad en el lado del receptor 7. Las Fig 3. y Fig 4. presentan las estructuras del paquete GFDM y OFDM, respectivamente, donde los símbolos de datos se distribuyen a lo largo del tiempo y la frecuencia (8).
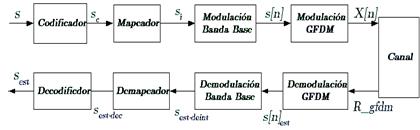
El modelo en bloque del sistema GFDM se ilustra en la Fig 5. El proceso de transmisión se describe de la siguiente manera, para transmitir la información binaria, el primer paso es la codificación de la información, en segundo lugar, se realiza la modulación de banda base, en este caso BPSK y QPSK. Luego, los símbolos de modulación se dividen en bloques que contienen M × N elementos 7,9.
En el lado del receptor, cada operación se proporciona de manera inversa de acuerdo con los pasos de procesamiento de la señal en el transmisor.
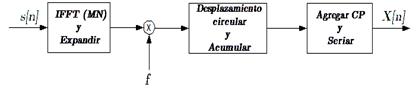
La Fig. 6 muestra el diagrama simplificado del transmisor GFDM que requiere un total de M operaciones de IFFT de tamaño MN. Los símbolos de datos de entrada
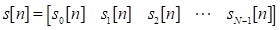 y la salida del transmisor GFDM se relacionan por el vector columna de dimensión MN y es expresado como:
y la salida del transmisor GFDM se relacionan por el vector columna de dimensión MN y es expresado como:
donde s e #091;n#093; es una versión expandida del vector s#091;n#093; con dimensión MN × 1 y puede ser expresado como,
donde
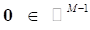 es un vector fila de ceros,
es un vector fila de ceros,
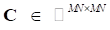 es una matriz circulante cuya primera columna está compuesta por el vector c
L
de dimensión MN × 1 dado por:
es una matriz circulante cuya primera columna está compuesta por el vector c
L
de dimensión MN × 1 dado por:
𝐹 𝑀𝑁 −1 es la matriz de transformada inversa de Fourier Discreta (inverse Discrete Fourier Transform, iDFT) de dimensión MN × MN. La ecuación (3) puede ser reescrita como,
donde,
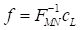 y c
L
corresponde al espectro discreto del formato de pulso. La selección de los mismos es de gran importancia para obtener un mayor desempeño del sistema. Esta investigación utiliza los coeficientes propuestos en (10.
y c
L
corresponde al espectro discreto del formato de pulso. La selección de los mismos es de gran importancia para obtener un mayor desempeño del sistema. Esta investigación utiliza los coeficientes propuestos en (10.
Alternativamente, Xn093 puede ser representado de forma matricial como en la expresión (8), donde G = diag (f) que representa una matriz identidad cuya diagonal principal está compuesta por el vector f:
Esto es posible porque
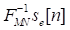 puede ser obtenido al aplicar M productos repetidos de
puede ser obtenido al aplicar M productos repetidos de
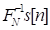 , es decir, si
, es decir, si
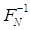 es una matriz de transformada inversa de Fourier Discreta de dimensión N × M entonces (8 ) puede ser expresada como:
es una matriz de transformada inversa de Fourier Discreta de dimensión N × M entonces (8 ) puede ser expresada como:
donde I N representa una matriz identidad de dimensión N × M y la matriz Z de dimensión MN × N está dada por
Para
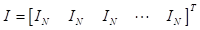 y de dimensión MN × N, (7) se puede expresar de manera alternativa como:
y de dimensión MN × N, (7) se puede expresar de manera alternativa como:
donde la matriz C nN es tal que su multiplicación por un vector de dimensión N es equivalente a realizar una operación de desplazamiento circular de periodo nN en ese vector. Entonces (11) se reescribe en forma matricial y al considerar (9), de la misma forma que en11, se tiene que:
donde
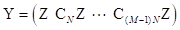 ,
,
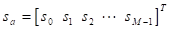 y el vector resultante X tienen dimensión MN × 1.
y el vector resultante X tienen dimensión MN × 1.
Una forma simplificada de expresar el vector de transmisión X en el sistema GFDM puede ser representado como la multiplicación de la matriz Y por el vector de símbolos, como:
con s a como el vector que tiene los M vectores de símbolos de N elementos organizados en el paquete GFDM.
La idea para desarrollar el receptor es una vez sometida al canal y luego de ser removido el CP el vector resultante es dado como:
donde n ~ N(0,σ2 I MN ) es el vector de ruido aditivo gaussiano blanco complejo (AWGN) con σ2 como la variancia del ruido (12)y el vector R gfdm tiene dimensión MN × 1.
Existen varios métodos de realizar la detección de la señal recibida como: Retorno a Cero (Zero Forcing, ZF), Filtro Acoplado (Matched Filter, MF) y Error cuadrático medio mínimo (Minimum Mean Square Error, MMSE) (13). En este trabajo es aplicado ZF a las matrices del canal y de transmisión GFDM, al multiplicar el vector recibido R
gfdm
por la matriz pseudoinversa
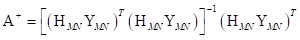 de dimensión MN × MN. El vector resultante de dimensión MN × 1 es dado como:
de dimensión MN × MN. El vector resultante de dimensión MN × 1 es dado como:
D. Canales de comunicación
El canal de comunicación está modelado por la matriz H que se debe al desvanecimiento a pequeña y gran escala 14 y por n que es el ruido aditivo Gaussiano blanco introducido por el receptor. Se va a considerar 3 tipos de matrices de canal H.
El primer canal se caracteriza por una matriz identidad 𝐻 de dimensión MN × MN, cuya diagonal principal está compuesta por unos. El segundo canal es una matriz H fija con L = 4 taps, por ejemplo
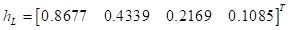 , estos se mantienen fijos durante los M espacios de tiempo del paquete GFDM, además, h
L
es un vector determinístico. La matriz H del tercer canal es fija-aleatoria, es aleatoria debido a que cada uno de los L = 4 taps representa una variable aleatoria Gaussiana Compleja de media 0 y varianza σ2 = 1, por ejemplo, h
L
= T, y es fija porque se mantiene iguales durante los M espacios de tiempo del paquete GFDM.
, estos se mantienen fijos durante los M espacios de tiempo del paquete GFDM, además, h
L
es un vector determinístico. La matriz H del tercer canal es fija-aleatoria, es aleatoria debido a que cada uno de los L = 4 taps representa una variable aleatoria Gaussiana Compleja de media 0 y varianza σ2 = 1, por ejemplo, h
L
= T, y es fija porque se mantiene iguales durante los M espacios de tiempo del paquete GFDM.
Parámetros de simulación
Los valores del pulso formateador son mostrados en la Tabla 1, los coeficientes g = 7 y g = 8 son seleccionados debido a que tienen mejor atenuación mínima de banda de paso (Minimum Stopband Attenuation, MSA) como es demostrado en (10).
TABLA 1: Coeficientes del pulso formateador
| Coeficientes | g = 7 | g = 8 |
| c0 | 1 | 1 |
| c1 | -0.9994 | 0.9993 |
| c2 | 0.9784 | 0.9820 |
| c3 | -0.8439 | -0.8942 |
| c4 | 0.5365 | 0.7071 |
| c5 | -0.2068 | -0.4476 |
| c6 | 0.03518 | 0.1887 |
| c7 | 0 | -0.0367 |
| MSA (dB) | 63.45 | 61.54 |
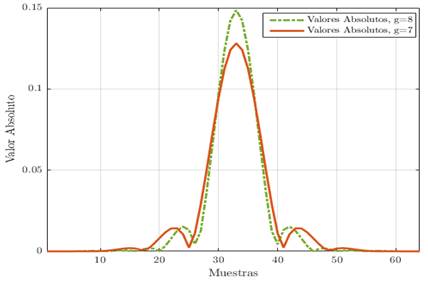
Los valores absolutos de 𝑓 son mostrados en la Fig.7 para g = 7 y g = 8, respectivamente.
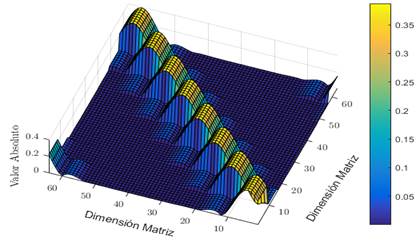
La matriz de transmisión Y en GFDM con parámetros M = 8 y N = 8 es presentada en la Fig 8.
A continuación, son descritos los diferentes tipos de matrices del canal de comunicación que son empleados para evaluar el desempeño del sistema GFDM. En primer lugar es mostrado el canal ideal con M = 8 y N = 8 que es representado por una matriz identidad. La matriz del canal ideal está conformada por la diagonal principal con unos y las diagonales secundarias llenas con ceros. Este canal no afecta a los datos transmitidos por el sistema de transmisión GFDM y es el la mismo para cada transmisión.
Para la conformación del canal fijo son empleados los coeficientes del vector h L = T. La matriz de canal es una matriz Toeplitz donde la primera columna está compuesta por el vector h L . Este canal provoca desvanecimiento selectivo en frecuencia y sin efecto Doppler. En cada transmisión mantiene el mismo comportamiento frente a los símbolos transmitidos por el sistema.
Por último, el tercer tipo de canal utilizado en esta investigación es una matriz fija aleatoria. Se caracteriza por ser una matriz Toeplitz donde los coeficientes de la primera columna están dados por el vector h L multiplicado por una variable aleatoria Gaussiana compleja con media (m = 0) y varianza (σ2 = 1). Este canal provoca mayor probabilidad de error debido a que varía de forma aleatoria en cada transmisión (un canal diferente en cada transmisión).
Resultados y Discusión
En esta sección son presentados los resultados de las simulaciones. El desempeño de las modulaciones BPSK y QPSK es medido en término del BER. Las Fig 9., Fig 10. y Fig 11. muestran claramente que existe un relacionamiento entre la Relación Señal a Ruido (Signal Noise Ratio, SNR) y BER. La relación muestra que las dos cantidades son inversamente proporcionales, por tanto, cuando SNR es mayor el BER decrece.
Esto provocado debido a que la cantidad de ruido decrece con el incremento de SNR y el nivel del BER también decrece con el incremento en SNR debido a que existe un relacionamiento directamente proporcional entre la potencia del ruido y el BER.
Las curvas de las figuras Fig 9., Fig. 10 y Fig 11. muestran el desempeño del sistema GFDM del modelo propuesto en la Sección II para las modulaciones BPSK y QPSK. La técnica de detección ZF fue aplicada al vector recibido para los diferentes tipos de canales de comunicación.
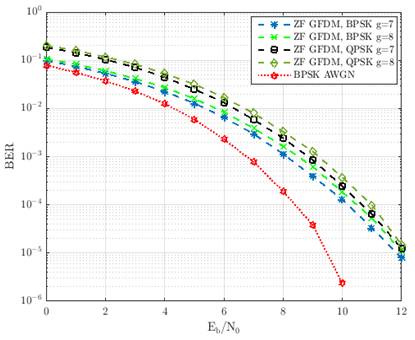
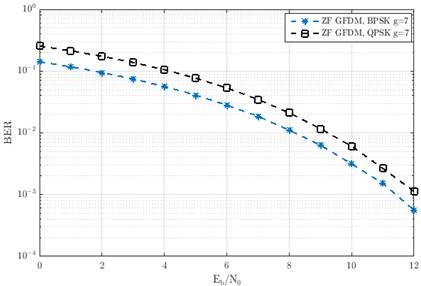
En la Fig 9. son mostradas las curvas de desempeños del sistema GFDM para las modulaciones BPSK y QPSK al utilizar los coeficientes de la Tabla 1 y los pulsos formateadores de la Fig 7. Estas curvas fueron obtenidas al emplear el canal de comunicación ideal mostrado en la sección anterior. En la Fig 9. es posible observar que para g = 7 en ambas modulaciones el comportamiento del desempeño del sistema GFDM es el mejor. Por tanto, las curvas de desempeño para los demás canales de comunicación son presentadas para este valor de g. Además, en la Fig 9. es apreciable que la modulación BPSK presenta mejor comportamiento que QPSK.
Las curvas de desempeños presentadas en la Fig 10. corresponden al sistema en presencia del canal fijo descrito en la sección anterior para g = 7. En la figura se puede observar que la modulación BPSK presenta mejor desempeño que QPSK cuando está en el BER de 10-4. Por otro lado, al comparar el desempeño del sistema en presencia del canal ideal y fijo se puede observar la degradación del rendimiento por causa del canal.
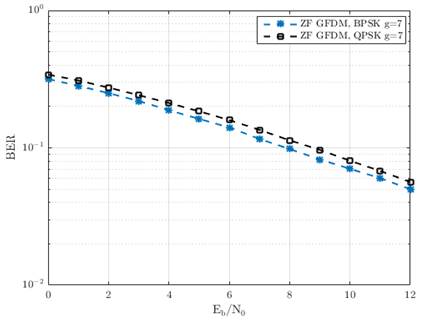
La Fig 11. muestra el comportamiento de las dos modulaciones en presencia del canal fijo aleatorio. Note que la modulación BPSK presenta mejor desempeño para este tipo de canal y debido a su característica la modulación BPSK tiende a tener el mismo desempeño que QPSK.
Conclusiones
En este trabajo se ha presentado y discutido la técnica de detección ZF en el sistema GFDM para diferentes esquemas de modulaciones y canales de comunicación. El modelo matricial para la señal transmitida en el sistema GFDM fue presentado en la Sección II, seguido del estudio del desempeño en presencia del detector ZF. Como resultado de la presente investigación se presentaron diferentes curvas de desempeños del sistema GFDM en diferentes condiciones. Se concluye que el esquema de modulación BPSK tiene mejor comportamiento estadístico para el canal ideal, fijo y fijo aleatorio en el sistema GFDM