1. Introducción

Los análisis de los eventos de precipitación extrema, son un componente esencial para el diseño en ingeniería, aún que varios autores (^{Abreu et al., 2004}; ^{Akerman, 2015}) en los patrones de las variables hidrometeorológicas están cambiando y se espera que en el futuro los desastres provocados por eventos extremos sean más frecuentes e intensos debido al calentamiento global lo cual según (^{Azizian, 2018}) aumenta la exposición de poblaciones e infraestructuras vulnerables a este problema. El dimensionamiento de proyectos concernientes a estructuras hidráulicas o algún proyecto de aguas requiere la determinación de la forma y el pico del hidrógrafo de proyecto. Obtener este hidrógrafo según varios autores citados en Castillo (²⁰²⁰) para un período de retorno (Tr) representa un problema arduo complejo. A día de hoy existen varios modelos matemáticos y combinaciones como los propuestos por (^{Upegui, 2020}) que simplifican los cálculos en las cuencas urbanas cómo SWMM y MIKE21.

El proceso de urbanización en los márgenes de los ríos puede ser informal o formal y es el responsable de muchos de los casos de inundaciones alrededor del mundo (^{Akerman, 2015}). La rápida urbanización produce un cambio significativo en el uso del suelo, dando una considerable expansión a las áreas impermeables y su influencia en los procesos de lluvia escorrentía (^{Freiria, 2014}; ^{Llecllish et al., 2017}). Lo cual, en el caso que nos ocupa, es la principal causa del estudio hidrológico que se realiza a los ríos que atraviesan la ciudad de Santa Clara.

Dentro de los parámetros empleados en la modelización hidrológica el tiempo deconcentración (tc) es uno de los fundamentales (^{Agua, 2015}). Según la definición de Chow y Maidment, el tiempo de concentración se precisa por:

Un concepto idealizado y definido como el tiempo que le toma una gota de agua de lluvia caída sobre el punto más remoto de un área de drenaje en llegar al punto de cierre de la cuenca, donde la lejanía guarda relación con el tiempo de viaje en vez de la distancia. Probablemente una mejor definición es que es el tiempo después del comienzo de la lluvia que demora toda el área de drenaje en contribuir simultáneamente al punto de cierre. (^{Chow, et al., 1988})

Se aplica en casi todos los modelos matemáticos y especialmente cuando se utilizan los hietogramas rectangulares (Soriano y Yuste, 2006) relacionados con la fórmula racional. La definición de tc considera la geometría, geología, tipo de suelo, uso del suelo, topografía y otras características hidráulicas de una cuenca hidrográfica (^{OMM, s.f}.).

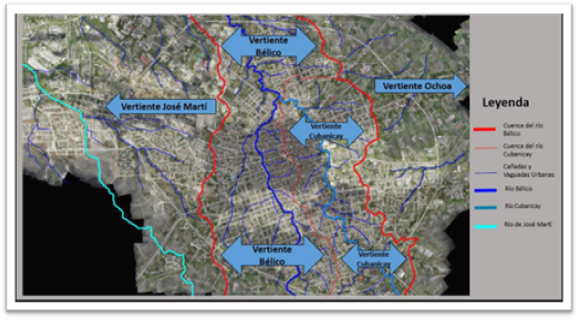
En esta investigación se realizó una valoración a partir de varios métodos empíricos para el cálculo del tiempo de concentración por medio de varias formulaciones empíricas existentes de las formulaciones empíricas existentes que son utilizadas comúnmente para este tipo de investigaciones. El objetivo principal del trabajo fue comparar el comportamiento del tiempo de concentración asociado a la cuenca de los ríos Bélico y Cubanicay para poder realizar recomendaciones técnicas asociadas al proyecto integral para el manejo del drenaje urbano de la ciudad de Santa Clara (véase la figura 1).

Figura 1 Ubicación general de los ríos objeto de estudio 

2. Metodología

Selección y definición de las principales formulaciones empíricas a utilizar y datos complementarios

Según (^{Chow, 1964}) entre un hietograma e hidrógrafo las relaciones de tiempo asociados al t. real de una cuenca, se muestran en la tabla 1.

Tabla 1 Conceptos asociados al tiempo de concentración 

El área comprendida bajo un hidrograma simple, es decir con un solo pico, corresponde al volumen de agua que ha pasado por el punto de aforo en el intervalo de tiempo determinado. El hidrograma producido por una tormenta conocida, se conoce como evento, en donde el tiempo base tb, es el tiempo transcurrido entre el momento en que empiezan a llegar las componentes de la escorrentía generadas por el aguacero y el momento en que estas ya dejan de actuar.

Según ONN (²⁰¹⁸), se considera que el tiempo de concentración puede definirse a partir de la observación de la escorrentía superficial. Si se aplica una lluvia uniforme a una cuenca, las zonas más cercanas a la salida contribuyen a la escorrentía casi de inmediato. Mientras la lluvia continúa, los aportes de las zonas de aguas arriba llegan posteriormente, hasta que el flujo de todos los puntos de la cuenca se concentra en la zona baja. Por lo tanto, el tiempo de concentración se corresponde con la duración necesaria, con lluvia uniforme, para que el total de la cuenca contribuya a la escorrentía directa en el tramo final del cauce.

Para la determinación de este parámetro, puede utilizarse un procedimiento de aproximación reiterativa para determinar el tiempo crítico de concentración (t.), donde existen varias rutas posibles que deben ser consideradas a partir de las particularidades de cada proyecto. El tiempo de concentración de cualquier punto en un sistema de drenaje urbano de aguas lluvias, es la suma del tiempo de entrada t. (tiempo que demora la gota de lluvia en llegar a los receptores pluviales) y del tiempo de flujo (t.) en las tuberías, ubicadas aguas arriba del flujo de salida en las zonas de captación de la cuenca urbana (^{Chow, 1994}) tal y como se expresa en la Ecuación 1.

(1)

Sin embargo, varios autores como (^{Upegui y Gutiérrez, 2011; Freiria, 2014}: ^{Castillo, 2020}) amplían la ecuación 1 a la siguiente expresión (ver ecuación 2):

(2)

Donde t. son los tiempos de viaje en distintos segmentos de la ruta más alejada del flujo, cada uno de estos tiempos pueden tener formulaciones distintas en correspondencia a las velocidades encontradas en ellos debido a sus características físicas. La ecuación 2 responde con mayor precisión a la definición, hay que tener en cuenta el recorrido que pueda realizar la gota de lluvia desde el punto más alejado hasta el punto de cierre, si consideramos una cuenca experimental imaginaria totalmente urbanizada podemos observar que la gota de lluvia desde su llegada a la superficie, realiza varios trayectos, si cae encima de pavimento, en un aguacero pronunciado se puede presenciar como el escurrimiento es a través de láminas desde el eje de la misma hasta la cuneta de drenaje, en ese caso las ecuaciones para hallar el tiempo en ese trayecto de viaje se le denomina flujo en lámina (sheet flow), al llegar a la cuneta en dependencia de la geometría que tenga esta última el flujo puede considerarse como sheet flow, shadow flow (flujo poco profundo) o channel flow (flujo en canal) (^{Chow et al., 1988}), lo que hace que su formulación de cálculo difieran, incluso en zonas donde la cuneta puede desparecer y se observa el flujo sobre el suelo, cambia la forma de enfrentar estos cálculos.

En el caso de cuencas urbanas es común que a las áreas de aporte a nodos de un sistema de drenaje no sobrepasen la cifra de 1 ha. Considerando una manzana de 100 m de largo y 100 m de ancho. Esto en cuencas urbanas se traduce a t. muy bajos que son limitados en la bibliografía a entre 5 y 10 minutos como mínimo (^{Agua, 2015}; ^{ONN, 2018}; ^{Azizian, 2018}).

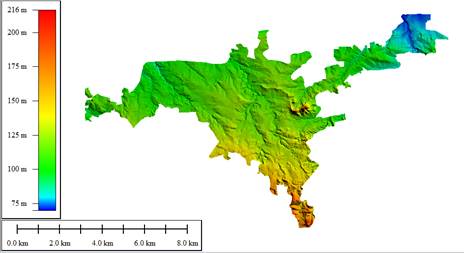
Dado que el concepto de tiempo de concentración tiene una cierta base física, han sido numerosos los autores que han obtenido formulaciones del mismo, a partir de características morfológicas y geométricas de la cuenca (^{Llecllish y Loayza, 2017}). En el siguiente epígrafe se muestran algunas de esas fórmulas para el cálculo de t. en cuencas urbanas y semi-urbanas o rurales de poco tamaño, las cuales serán aplicadas a la cuenca del río Bélico y Cubanicay en la ciudad de Santa Clara. Es importante mencionar que para su cálculo es imprescindible conocer las futuras condiciones del uso del suelo (^{Chow, 1964}). Para la delimitación de la cuenca fue utilizado un Modelo Digital de Elevación (MDE) elaborado en 2016 por el Grupo empresarial GEOCUBA Villa Clara-Sancti Spíritus, adquirido por la Empresa de Proyectos e Investigaciones Hidráulicas de Villa Clara (IPH VC) con precisión aceptable para el estudio de los parámetros morfo-geométricos de la cuenca, necesarios para el cálculo de los diferentes métodos implementados. El MDE se trabajó en el software AutoCAD Civil 3D para ubicar un punto de cierre en el río y definir el área de aporte o cuenca que tributa escurrimiento en este lugar de manera totalmente digital acorde al modelo de elevación disponible (véase la figura 2).

Figura 2 Representación del MDE utilizado en el estudio de los ríos Bélico y Cubanicay 

La fórmula racional es uno de los modelos matemáticos de lluvia escorrentía más utilizados en diversos lugares del mundo (^{OMM, s.f}.; ^{Soriano y Yuste, 2006}; ^{Upegui y Gutiérrez, 2011}). En el caso de su formulación, se toma la intensidad probable para el tiempo de concentración de la cuenca de estudio. Para la aplicación de este modelo es necesario contar con Curvas de Intensidad-Frecuencia-Duración las cuales son comúnmente usadas en recursos hídricos para dar soportes al planeamiento y diseño de estructuras hidráulicas.

La hipótesis fundamental en el diseño hidrológico por el método Racional radica en la suposición de que la duración de la lluvia máxima o de diseño coincide con el tiempo de concentración de la cuenca, ya que las lluvias de mayor duración no producen un aumento en los caudales punta. Sin embargo, establece una diferencia importante al destacar que el tiempo de concentración es la fase del aguacero que determina el caudal máximo, y esta fase puede ser igual o no a la duración del aguacero, ya que la duración de la lluvia no está relacionada con el tamaño de la cuenca y es solo función de variables climáticas. Por lo que la lluvia asociada a los caudales máximos se refiere al intervalo más intenso de duración igual al tiempo de concentración, pero esa duración no equivale a la duración del aguacero, ya que solo una fase del aguacero puede ser suficiente para generar una creciente si el suelo se encuentra saturado.

Fórmulas para el cálculo del tiempo de concentración

Las fórmulas empíricas son expresiones matemáticas que sintetizan, mediante regresiones, correlaciones u otros medios numéricos, una serie de resultados observados en diversos ensayos, sin necesidad de disponer de una teoría que la sustente. En hidráulica se utilizan con frecuencia fórmulas empíricas para la determinación de diferentes variables, como el tiempo de concentración de una cuenca t..

Para el cálculo del t. (en horas):

· Kirpich: Quizás la fórmula más utilizada a nivel mundial para hallar t.. Se estimó originalmente para cuencas de Tennessee y Pennsylvania en los Estados Unidos entre áreas de 0.004 y 0.45 km. con pendientes entre 3 % y 12 % y con significante flujo de canales (^{Llecllish y Loaiza, 2017})

Posee dos expresiones fundamentales: (^{Azazian, 2018})

(3) (Kirpich-Tennessee en 1940)

(4) (Kirpich- Pennsylvania en 1940)

· Bransby-Williams: Sugerida por The Institution Engineers, Australia en remplazo de la fórmula de Kirpich, al obtener estos valores de t. muy bajos con respecto a los parámetros medidos (^{Llecllish y Loaiza, 2017}).

(5) (ASDOT en 1995)

· California Culverts Práctice: Modificación de la ecuación de Kirpich; desarrollada para pequeñas cuencas montañosas en California. Es la fórmula oficial de la NC 1239-2018 para el cálculo del t. en el drenaje pluvial.

(6) (CDH en 1960)

· Carter: Está datada con cuencas urbanas de los Estados Unidos con áreas menores a 20.72 km. y pendientes menores a 0.5% (^{Azazian, 2018}).

(7) (Carter en 1961)

· Chow: Calibrada en 20 cuencas rurales de entre 0.01 y 18.2 km., con pendientes entre 0.5 y 9 % (^{Azazian, 2018}).

(8) (Chow en 1961)

· FAA: Fórmula de la Federal Aviation Administration elaborada en 1970 con calibraciones en aeropuertos con lo cual es ideal para áreas urbanizadas (^{Azizian, 2018}).

(9) (FAA en 1961)

· Kerby-Hathaway. Ecuación elaborada a partir de inundaciones en cuencas experimentales urbanas menores a los 0.1 km. y con longitudes menores a los 0.37 km. (^{Azizian, 2018})

(10)

· SCS Lag. Ecuación desarrollada por el Servicio Conservación del Suelo de Estados Unidos (Soil Conservation Services) a partir de la información de cuencas de uso agrícola; ha sido adaptada a pequeñas cuencas urbanas con áreas inferiores a 8 km., se ha encontrado que generalmente es buena cuando el área se encuentra completamente pavimentada; para áreas mixtas tiene tendencia a la sobreestimación. (^{Chow, et. al, 1988})

(11)

· Corps of Engineers: Datada en 25 cuencas rurales con áreas menores a 12 km. (^{Azazian, 2018}).

(12)

Donde: A, área de la cuenca en km.; C, coeficiente de escorrentía de la fórmula racional; CN, Número de Curva del SCS; H, diferencia de cotas del cauce en m; L, longitud del cauce en km; S, pendiente del cauce principal m/m; N, coeficiente de retardo; n, coeficiente de rugosidad de Manning.

· Área de estudio

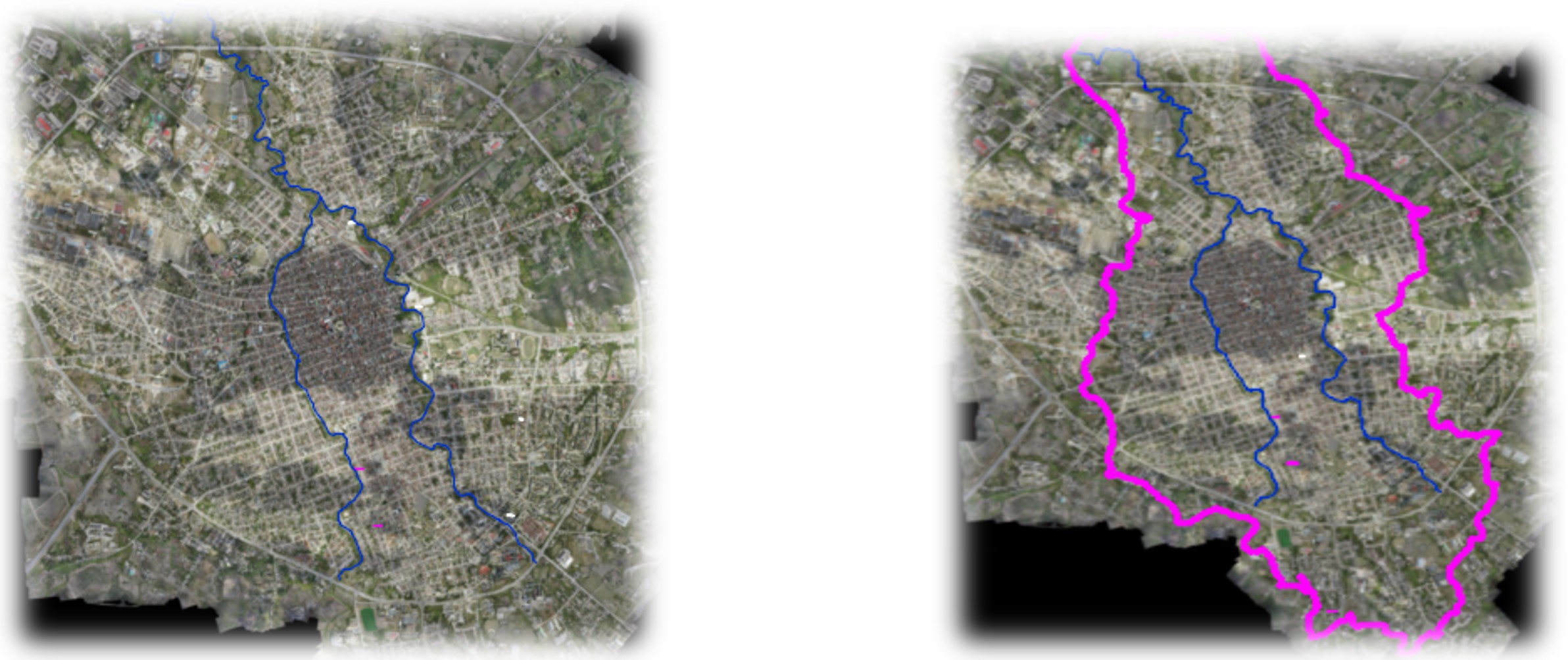
La cuenca urbana del río Bélico es predominantemente llana, típica de la zona hidrológica central de Cuba y ha sido seleccionada como cuenca experimental dada su cercanía a la Universidad Central “Marta Abreu” de Las Villas, su ubicación en la ciudad de Santa y a la situación actual del drenaje deficiente debido a las incorrectas políticas urbanísticas de la ciudad que han provocado la disminución de los cauces de los afluentes y ríos principales. El punto de cierre de la cuenca se define en la Circunvalación Norte, hasta este lugar la cuenca posee dos ríos o afluentes principales, el Bélico y el Cubanicay que nacen en las cercanías de la Circunvalación Sur y atraviesan el centro urbano de sur a norte (véase lafigura 3).

Para obtener los parámetros requeridos en las ecuaciones de tiempo de concentración, dígase longitud del cauce, pendiente media del cauce y área de la cuenca se utiliza el software AutoCAD Civil 3D v2015 como una herramienta para el dibujo de elementos vectoriales y para la digitalización. La gran capacidad del software permite trabajar con una cantidad considerable de datos de campo y realizar grandes análisis como la modelación de superficies de terreno, curvas de nivel, el diseño de secciones y el cálculo ágil de áreas y volúmenes que le faciliten al profesional la toma de decisiones en un proyecto específico. En este caso, el software es utilizado para un comando llamado Catchments que permite definir un punto de cierre en cualquier lugar del MDE y define el área tributante a ese punto, que no se representa en lafigura 3 ya que el objeto de mayor interés es la zona urbana.

Se definen entonces los parámetros geométricos fundamentales de la cuenca:

· Área (A): 13.51 km.

· Longitud del cauce principal (L): 7.12 km

· Desnivel del cauce principal (H): 44.56 m

· Pendiente del cauce principal (S): 0.00625 m/m

La cuenca cumple con la mayoría de las recomendaciones para la aplicación de las diez fórmulas anteriormente descritas. Ahora es necesario la elección de los parámetros hidrológicos-hidráulicos, para este estudio se escogieron los siguientes:

· Número de curva NC (SCS): El valor del número de curva recomendado por Chow et al. (¹⁹⁸⁸) en áreas urbanas en climas tropicales es 95 en nuestro caso se asumirá 90.

· Coeficiente de retardo N: Según Akerman (²⁰¹⁵) en cuencas urbanas este coeficiente varía entre 0.02 y 0.08 el valor elegido para la cuenca del río Bélico es 0.05.

· Coeficiente de rugosidad de Manning (n): Para la elección del coeficiente se supone un cauce marcado por el crecimiento de árboles y matorrales densos que son comparables con la urbanización, el valor escogido 0.09 (^{Chow, 1994}).

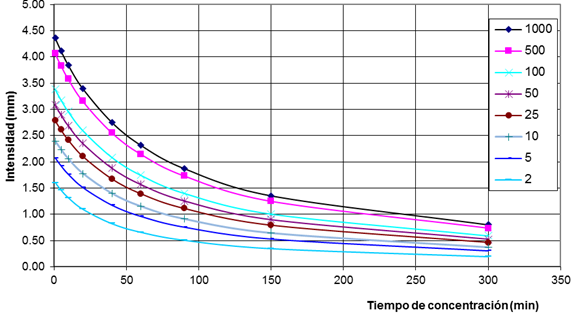
· Intensidad máxima de precipitación i: Para la realización de este trabajo se utilizaron las curvas IFD para la región central elaboradas por Abreu et al. (²⁰⁰⁴) las cuales poseen forma de curva típica (consultar ecuación 12 y figura 4).

(13)

Donde: A, B y n son coeficientes que dependen de la región hidrológica analizada, sino que fueron considerados a partir de los estudios presentados por Abreu et al. (²⁰⁰⁴), actualizados por Castillo (²⁰²⁰).

Figura 4 Curvas IFD para la región central de Cuba Fuente Abreu et al 2004 

Para el caso de estudio, la Norma Cubana 1239-2018 que rige los procedimientos para el drenaje pluvial urbano en Cuba, se considera al río como medianamente denso con respecto a la cantidad de habitantes por km. que habitan a sus alrededores, por tanto, se toma una probabilidad de diseño del 2 % o 50 años de período de retorno, de esta manera se trabaja con la ecuación 13 de curva expresada la .: mm/min.

(14)

Figura 3 Ríos Bélico y Cubanicay a la izquierda y cuenca tributaria a la derecha 

3. Resultados

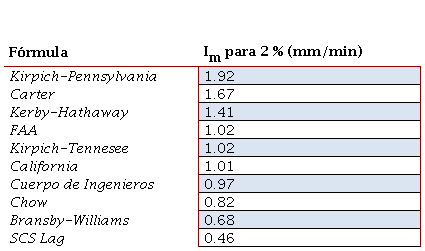
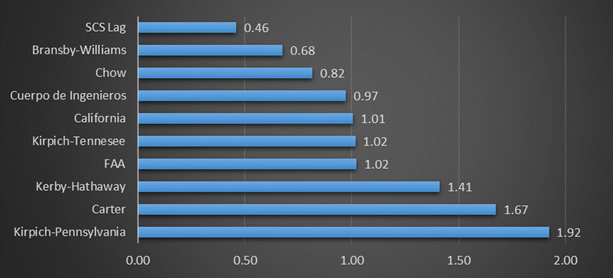
Los resultados de la estimación del tiempo de concentración son muy diferentes entre sí ya que cada autor estima su ecuación para cuencas con características muy particulares, por lo que debe tenerse mucho cuidado para la selección del valor más adecuado para el tiempo de concentración (véase la figura 5).

A simple vista se saca la conclusión de que los valores de las ecuaciones del SCS Lag, Carter y Kirpich-Pennsylvania son los más alejados de la tendencia.

Suponiendo una ecuación típica de tc:

(15)

Donde:

· K1: Coeficiente de ecuación de retardo

· K2: Coeficiente que depende de características hidráulicas-hidrológicas de la cuenca.

· K3: Coeficiente de parámetros geométricos L y S.

Los valores de K1 de las ecuaciones señaladas son de los más bajos mientras el valor de K2 y K3 en la ecuación SCS Lag es el más alto (véase las tablas 2 y 3).

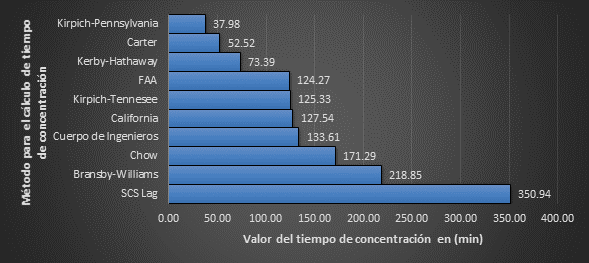
Figura 5 Gráfico de los resultados del TCNota: Se observan los valores de FAA; 318 Kirpich; California y Cuerpo de Ingenieros como valores centrales próximos a los valores reales a actualizar en la cuenca según Abreus et al (2004). 

Tabla 2 Valores de Kn para las distintas fórmulas valoradas 

Tabla 3. Resultados estadísticos principales del tc calculado con las distintas fórmulas 

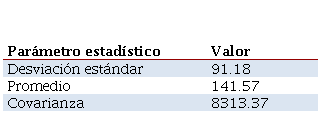
Para seguir el análisis se realizaron los estudios estadísticos de la intensidad máxima de precipitación (I.) (véase las tablas 4, 5 y figura 6).

Tabla 4. Cálculo de la Intensidad máxima de precipitación

Tabla 4 Cálculo de la Intensidad máxima de precipitación 

Tabla 5 Valores estadísticos fundamentales de Im 

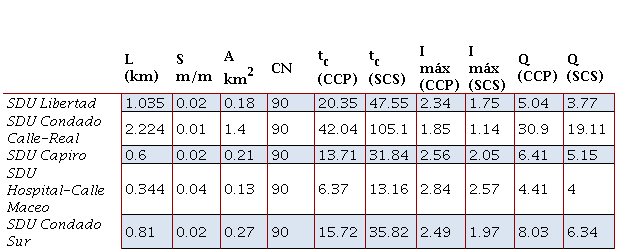
Con estos resultados es necesaria una comparación de la ecuación de California Culverts Practice (CCP) recomendada en la NC 1239-2018 para el cálculo del drenaje pluvial urbano con la ecuación del SCS que es la que menores resultados brindan con respecto a I.. Esta comparación se realiza a partir de cinco áreas hidrológicas urbanas (AHU) definidas en la tesis “Estrategias para la concepción de Sistemas de Drenaje Urbano en la ciudad de Santa Clara” elaborada por Castillo (²⁰²⁰) para definir el cambio de los gastos máximos de escurrimiento con respecto al cambio del método de cálculo de t. (véase la tabla 6).

Tabla 6 Comparación de CCP y SCS para áreas hidrológicas de Santa Clara 

El valor mínimo del tiempo de concentración de la norma es de diez minutos, por lo que el valor de intensidad del SDU Hospital Calle Maceo es reducido a prácticamente el mismo del SDU Capiro. La muestra consideró áreas hidrológicas vertientes al río Bélico, con distintos valores de A y L, lo que favorece trabajar en un rango aceptable de valores.

Los resultados anteriores evidencian que el método SCS es un método menos conservador a la hora de brindar un tiempo de concentración de diseño en áreas hidrológicas de aporte mayores a 0.1 km. lo que lo hace un método efectivo para el diseño de redes de drenaje pluvial urbano en áreas superiores a 0.1 km. lo cual ayuda a no sobreestimar los gastos de diseño a partir de la fórmula racional.

Figura 6 Gráfico de Im se observa la media alrededor de los 1 y 1.10 mm/min 

4. Conclusiones y recomendaciones

De acuerdo con los resultados obtenidos se llegó a las siguientes conclusiones:

1. El tiempo de concentración de una cuenca es un parámetro muy difícil de determinar cuando no se cuentan con mediciones que permitan su validación con las fórmulas empíricas.

2. Existen en el mundo varias fórmulas de t. generalmente basadas en la expresión de componentes L y S de la geometría de la cuenca, aunque este parámetro no depende solo de estos, es necesario realizar un análisis detallado de los métodos de onda cinemática ya que estos tienen intrínsecamente en sus formulaciones parámetros hidrológicos e hidráulicos que son parte importante del t. como la Intensidad máxima de precipitación y el coeficiente n de Manning.

3. El estudio comprueba que la fórmula propuesta por la NC 1239-2018 (California Culverts Practice) brinda un valor cercano al promedio de las fórmulas de t. con las características de L y S como base fundamental de cálculo.

4. Las fórmulas de t. para las condiciones de la ciudad de Santa Clara se dividen en tres subgrupos fundamentales:

a. Fórmulas no conservadoras: Aquellas cuyo valor de t. es superior a la media. (SCS Lag, Bransby-Williams, Chow).

b. Fórmulas de la media: Aquellas cuyo valor de t. coinciden prácticamente con el valor promedio de las ecuaciones analizadas (Cuerpo de Ingenieros, California Culvert Práctice, Federal Aviation Agency, Kirpich-Tennessee).

c. Fórmulas conservadoras: Aquellas cuyo valor de t. es inferior al de la media. (Kerby-Hathaway, Kirpich-Pennsylvania, Carter).

5. En el análisis hidrológico de los ríos Bélico y Cubanicay para el proyecto integral de drenaje urbano de la ciudad de Santa Clara se recomienda la ecuación de California Culvert Practice mientras no se conozca el tiempo de retardo de la avenida en el río Bélico con punto de cierre en la Circunvalación Norte.

6. Para el análisis de áreas hidrológicas pequeñas o subcuencas urbanas perteneciente a los ríos Bélico y Cubanicay se recomienda la ecuación del SCS Lag utilizada en muchos países para calcular t. en cuencas urbanas y diseñada para este tipo de trabajos.

7. Se define el tiempo de concentración teórico de la cuenca del río Bélico en el punto de cierre ubicado en el puente de Circunvalación Norte en 128 minutos (dos horas aproximadamente).

Luego de haber expuesto las conclusiones previas se recomiendan los siguientes aspectos:

1. Este tiempo de concentración calculado solo es una aproximación teórica por lo cual es necesaria su validación mediante técnicas de medición en puntos a determinar dentro de la ciudad y en el punto de cierre para obtener el valor real del mismo.

2. Es necesario recordar que la ciudad de Santa Clara posee una situación muy tensa con el drenaje de los ríos fundamentales y una de las causas es la pérdida de los cauces naturales en detrimento de la nueva urbanización, esta fórmula no tiene en cuenta esta situación.

3. En caso de que el proyectista decida ser un poco conservador o menos se propone la utilización de:

a. La fórmula de Chow con tiempos de concentración más altos.

b. La fórmula de Kerby-Hathaway con tiempos de concentración más bajos. Haciendo la salvedad de que para el caso de que se utilice la fórmula es responsabilidad de este trabajo su definición a pesar de que la cuenca no cumpla con las características con las cuales fue elaborada.