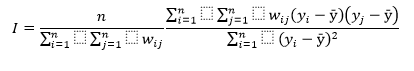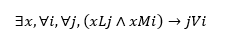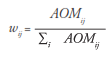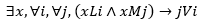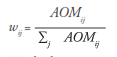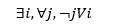Introducción
México enfrenta una crisis de homicidios. Los grupos del crimen organizado (GCO) entraron en guerra al final del siglo XX (Trejo y Ley 2022), y la violencia creció de manera exponencial cuando el presidente Felipe Calderón declaró la guerra contra el tráfico de drogas (Mattiace y Ley 2022). De menos de 10 mil homicidios en 2007, pasamos a más de 25 mil en 2010. Desde entonces, la violencia no ha parado de crecer. Las guerras entre grupos rivales se multiplican, y de su conflicto ha surgido una compleja geografía de la violencia.
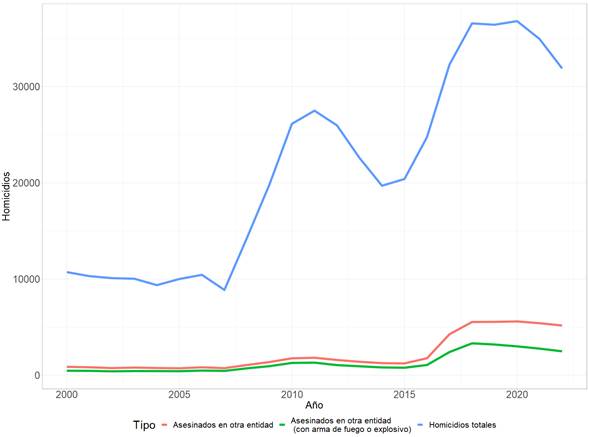
Sin embargo, desde 2017 emerge un fenómeno adicional: el número de personas asesinadas en un municipio distinto al municipio en que residen (es decir, personas asesinadas en otro municipio, AOM) pasó de una media de 1000 a una media de 5000. Este cambio abrupto se puede observar en el gráfico 1. Creemos que el flujo de los AOM permite reconstruir la actual geografía de la violencia.
Fuente: elaboración propia con base en INEGI, Defunciones registradas.
Gráfico 1. Homicidios dolosos en México 2000-2022
Cuando una persona que vive en un municipio fallece en otro, se puede inferir que hay una relación entre esos municipios. Cuantas más personas de uno mueren en el otro, más fuerte es el vínculo entre estos, y lo que se transmite a través de ese vínculo es precisamente la muerte. El vínculo entre lugares de residencia y lugares de defunción puede indicar el vector de contagio, es decir, el mecanismo y la ruta de propagación de los homicidios dolosos entre municipios en México.
El vector son las personas que participan en los enfrentamientos entre grupos del crimen organizado. Mientras que Prieto-Curiel, Campedelli y Hope (2023) hablan de “afiliados a organizaciones criminales“, y Lopez-Cruz y Torrens (2023) hablan de “level of guns“, Magaloni et al. (2020) prefieren la expresión “hombres armados que sirven como asesinos“ y Pereda (2018) habla de pistoleros (“gunmen”). En este trabajo, creemos que el término “sicario” es más adecuado en el habla hispana y comprende mejor estas acepciones.
Si los AOM representan el flujo de sicarios de las organizaciones delictivas, podrían ayudar a entender cómo se difunde el homicidio entre los municipios de México y a resolver la tensión entre dos hipótesis centrales sobre la geografía de las guerras criminales. La primera sugiere que los GCO relocalizan sus actividades conquistando e invadiendo nuevos territorios (hipótesis centrífuga). La segunda hipótesis argumenta que, al expandirse a otros territorios, alteran el equilibrio de poder en su propia región (hipótesis centrípeta). Los AOM pueden ayudar a determinar cuál, si acaso alguna, es la hipótesis correcta.
Nuestro objetivo no es brindar una explicación exhaustiva de la distribución espacial del homicidio, sino determinar cuál de las hipótesis, centrífuga o centrípeta, cuenta con mayor soporte empírico. Creemos que los patrones de AOM reflejan el flujo de sicarios consistente con cada hipótesis.
En las líneas siguientes, comenzamos por exponer el estado actual de la investigación sobre el homicidio en México y el lugar de nuestras hipótesis en este contexto. En segundo término, presentamos los datos y el método: la manera como los AOM permiten reconstruir los vectores del contagio de homicidio entre municipios. Enseguida, la sección de resultados documenta los hallazgos, y la sección final explora su relevancia teórica.
Aumento y difusión espacial de los homicidios
Los estudios cuantitativos sobre la violencia asociada al crimen organizado en México han llegado a dos grandes consensos. El primero consiste en que, si el Gobierno ataca a un GCO que opera en una región dada, la violencia aumentará en esa región. Se ha probado que la intervención del ejército aumenta la tasa de homicidios (Flores Martínez y Phillips 2022), y que la violencia inducida por el Gobierno, vía incursiones militares, es uno de los principales factores en la explicación del aumento de la violencia (Lopez-Cruz y Torrens 2023).
Este aumento de la violencia puede atribuirse a diversos factores. En primer lugar, el arresto o el homicidio de líder de la organización aumenta la violencia porque a) desata luchas de sucesión; b) crea incentivos para que otros grupos ataquen, y traten de controlar las rutas y territorios; c) rompe la cadena de mando, y hace que los grupos locales intenten sustituir sus ganancias mediante el crimen, o d) la organización intenta tomar represalias contra el Estado (Calderón et al. 2015).
Además, la aplicación de la ley puede disminuir la violencia contra las autoridades, pero desata nuevos episodios de violencia entre organizaciones (Friman 2009) o contra civiles (Márquez-Muñoz y González Ulloa 2023). Se ha destacado que asesinar o aprehender a los líderes de las organizaciones tiene un efecto positivo e inmediato en la fragmentación de los cárteles, y que hay una relación positiva entre los niveles de fragmentación de los GCO y los niveles de violencia (Contreras Velasco 2023); a medida que aumenta la presión de las autoridades, también crece el número de GCO en un territorio, lo que puede intensificar la violencia entre ellos (Atuesta y Ponce 2017; Jones et al. 2022). Junto a la fragmentación, también surgen alianzas para defender el territorio; para enfrentar al Gobierno o a otra organización, o para perseguir a las facciones remanentes de una fragmentación (Atuesta y Pérez-Dávila 2018).
La violencia contra el Estado puede ser la opción racional para los carteles, cuando se los ataca de manera incondicional (Lessing 2015) o cuando no se llega a un acuerdo sobre el monto de los sobornos (Lessing 2013). La violencia también puede ser útil para confundir a las autoridades y hacer que persigan a sus competidores (Zepeda Gil 2021). Los GCO compiten por derecho a pagar a los funcionarios corruptos que controlan canales de tráfico específicos (Reuter 2009), pero pueden empeñarse en la violencia incluso cuando preferirían desistir, por el hecho de haber quemado sus naves (Pereda 2018). Cuando un exceso de violencia mina su opción de salida, los grupos criminales se ven obligados a cometer actos violentos que van en detrimento de sus objetivos comerciales, pero que son necesarios para que el grupo y sus miembros subsistan.
El segundo consenso indica que, si el Gobierno ataca a una organización criminal que opera en una región dada, la violencia también aumentará en otras regiones. Flores y Rodriguez-Oreggia (2014) observaron patrones de difusión de los homicidios hacia municipios contiguos a los que habían tenido un operativo conjunto. En tanto, Fuerte-Celis y Sánchez-Castañeda (2021) mostraron que el homicidio exhibe una tendencia creciente hacia la concentración espacial; entre 2000 y 2012, esto resultó en la formación de 18 clústeres de violencia. Calderón y sus colegas señalan que, entre 2006 y 2010, se observaron homicidios asociados a los GCO en 1132 municipios, de los cuales solo 20 concentraban el 50 % de las muertes por conflicto de narcotráfico (Calderón et al. 2015).
Se han propuesto diversas maneras de explicar estos patrones espaciales de violencia en México. Schatz y Tobias (2021) sugieren que la estrategia de atacar a los líderes de los carteles ha fragmentado sus estructuras de mando, lo que ha provocado una dispersión de la violencia que el Gobierno no ha logrado contener. Por otro lado, Franco-Vivanco (2023) plantea que la presencia de oleoductos en ciertos municipios puede dar pie a un efecto de “derrame” de la violencia hacia municipios vecinos. Esto se debe a que los carteles compiten por controlar estos recursos para financiar sus actividades ilícitas. Además, la violencia tiende a propagarse hacia áreas más aisladas de la red de hidrocarburos, donde el Gobierno enfrenta mayores desafíos para protegerla (Lopez-Cruz y Torrens 2023).
Asimismo, se ha indicado que la violencia se extiende hacia municipios estratégicos que están bien conectados por la red de transporte, como aquellos con aeropuertos o carreteras importantes (Shirk y Wallman 2015). También se ha señalado que, cuando se detiene a tenientes de los carteles, la violencia puede expandirse hacia los municipios el bajo control de aquellos, debido a que la cadena de mando se interrumpe en esos lugares (Calderón et al. 2015).
Una explicación adicional proviene de Trejo y Ley (2022). Los autores distinguen entre las sedes y los lugares de residencia de los GCO, y explican la propagación de los homicidios en estos lugares como resultado de los ataques y contraataques entre estas organizaciones, que a menudo cruzan fronteras estatales. Otros indican que ciertos municipios pueden ser la retaguardia de otros (San Román Tajonar 2020; Saucedo 2019), y Lessing (2015) ha señalado que las guerras criminales son siempre guerras de conquista. Prieto-Curiel, Campedelli y Hope (2023) destacan que la violencia es más intensa cuando se extiende más allá de los límites estatales. Por otro lado, la ausencia de patrones claros de contagio a nivel estatal (Korman 2019) es señal de la naturaleza selectiva de estos procesos espaciales, que operan a nivel de grupos de municipios.
Estas explicaciones son sugerentes pero limitadas. En primer lugar, han restringido el análisis de la difusión hacia municipios colindantes (con la excepción de Trejo y Ley, 2022); en segundo lugar, al utilizar métodos de autocorrelación espacial, dan la misma importancia a todos los municipios vecinos y suponen que la relación entre el municipio que contagia y el municipio contagiado es simétrica (es decir, el método implica que el contagio es de dos vías). Todas las hipótesis son post hoc (Merton 2013; Ragin 2007), en el sentido de que intentan explicar un patrón espacial ya observado, pero ninguno de los estudios ha sido diseñado con el objetivo de probar esas hipótesis. Además, cuanto más ambiguos y generales son sus planteamientos, menor es su contenido empírico y más difícil es falsearlos. Distintas hipótesis pueden ser compatibles con el mismo conjunto de datos, lo que las vuelve, para todos los efectos, intercambiables. No hay manera de decidir cuál, si alguna, es verdadera.
Solo dos hipótesis, surgidas en el trabajo de Melissa Dell (2015), son específicas en el grado suficiente para multiplicar sus consecuencias observables (King, Keohane y Verba 2018) y deducir de ellas hipótesis rivales. Osorio (2015) las ha llamado las hipótesis centrífuga y centrípeta. El objetivo de este trabajo es determinar cuál, entre estas dos hipótesis, cuenta con mayor soporte empírico.
La hipótesis centrípeta
Según Dell (2015), cuando el Gobierno ataca a un grupo criminal, crea incentivos para que grupos rivales intenten conquistar su territorio. Estos incentivos son más fuertes cuando el territorio objetivo está cerca, ya que su control implica dominar toda una región. La intervención estatal perturba el equilibrio militar entre GCO, lo que de manera indirecta fortalece la posición de los rivales (Osorio-Beristain 2021).
Osorio (2015) propone una formalización más elaborada, en dos etapas. Primera etapa: sean dos municipios j e i, cada uno con dos organizaciones rivales: a j y b j , en el primero, y c i y d i , en el segundo. Los dos grupos en cada municipio tienen una relación militar estable. Cuando las autoridades intervienen en el municipio j, minan la posición del grupo a j . Esto incita a b j a atacar a a j ; más aún: crea incentivos para que c i , que está en otro municipio, también ataque. En la formulación de Bullock (2021), la represión estatal debilita a los grupos criminales, lo que hace que los territorios bajo su dominio se vuelvan objetivos atractivos para sus rivales, que se ven atraídos desde lejos con la perspectiva de la conquista territorial. Así, los GCO invaden a los vecinos debilitados por la aplicación de la ley. Al alterar el equilibrio militar entre organizaciones rivales de tráfico de drogas, el Gobierno causa un desequilibrio en la estabilidad territorial y atrae a organizaciones rivales que luego intentan reclamar el dominio sobre el territorio (De Schutter, Duquet y Auweele 2023).
Considerada solo la primera etapa, la hipótesis centrípeta es una teoría sobre el aumento de los homicidios en el municipio j, no una teoría sobre su propagación hacia (o desde) otras regiones. Es una teoría de la difusión de los homicidas, no de los homicidios. Sin embargo, la segunda etapa añade complejidad a la teoría.
Segunda etapa: el momento espacial se inicia al terminar la batalla en el municipio j. La organización c i , que ha enviado grupos armados desde el municipio i para atacar a a j , pudo ganar o pudo perder. Como resultado, puede tener más recursos o menos recursos. En cualquiera de los dos casos, esto altera el equilibrio de poder en su municipio de origen i: si c i es ahora más fuerte que su rival original d i , puede atacarlo; si es más débil, será atacado. La intervención del grupo c i en el municipio j afecta el equilibrio militar en su propio municipio, i. La violencia en el municipio j retroalimenta la violencia en el municipio i, pero solo porque desde el municipio i se enviaron sicarios al municipio j. La violencia se propaga desde los municipios j hacia los municipios i que enviaron sicarios. El mecanismo no es ya el envío de grupos armados, sino que el resultado de las batallas en j crea incentivos para una guerra interna en i.
La hipótesis centrífuga
De acuerdo con Dell (2015), los ataques del Gobierno tienen dos efectos: a) reducen las rentas de los GCO locales y, con ello, b) disminuyen, para otras organizaciones, los costos de tomar el control del municipio atacado. Cuando un lugar se vuelve menos propicio para las actividades ilícitas, el crimen organizado se desplaza a otro lugar. Esto afecta a los niveles de violencia en la zona de destino. Así, cuando las autoridades atacan un lugar, parte de la violencia se desvía a otro lugar, sin que se la reduzca de manera sustancial. Los ataques del Estado en un municipio afectan a la violencia en otros municipios, al motivar a los traficantes a relocalizar sus actividades.
Lopez-Cruz y Torrens (2023) agregan que, cuando el Gobierno ataca un lugar j, la organización dominante no puede proteger sus ganancias, y esto induce a los otros a invertir en armas para apoderarse de ese lugar. Las pérdidas de la primera la obligan a diversificarse y expandirse hacia lugares i con otra estructura de oportunidad. Pero estos sitios i están en disputa, entonces, aumentan los homicidios, porque hay más armas y lugares en disputa. La violencia en j ocasiona la conquista de i y, por lo tanto, el aumento de la violencia en i. El número de homicidios en cada municipio es función de la inversión en armas (o del número de sicarios movilizados para conquistarla o protegerla) y del valor de la región en disputa. Toda vez que los lugares valiosos para el tráfico de drogas no coinciden con los lugares valiosos para otros delitos, como el robo de hidrocarburos, hay un cambio en el patrón espacial de la violencia.
En esta hipótesis, la violencia en el municipio j causa la violencia en el municipio i, porque desde el municipio j se enviaron sicarios al municipio i (al revés que en la hipótesis centrípeta). La violencia se propaga desde los municipios j hacia los municipios i a los que se enviaron grupos armados.
Comentario sobre las hipótesis
No solo la intervención del Gobierno puede debilitar a un GCO: que no intervenga puede tener el mismo efecto. Si el poder público se redistribuye, por un proceso electoral, y la organización a en el territorio i ya no cuenta con la protección de las autoridades, el efecto es el mismo que si el Gobierno la hubiera atacado: es vulnerable. Si el equilibrio de poder se rompe, otros pueden atacar. Esto puede alterar el equilibrio de poder en otros municipios o motivar que la organización atacada explore nuevos territorios. En este sentido, las hipótesis pueden ser consistentes con las aportaciones de Trejo y Ley (2022) sobre los procesos electorales como motores de la violencia. Por lo demás, una vez que el mecanismo se ha puesto en marcha, son dos problemas distintos saber cómo empezó y saber cómo opera. Aquí nos ocupamos del segundo tipo de problema.
Ninguna de las hipótesis requiere simetría en el contagio ni que los municipios i y j sean contiguos. Lo que ambas hipótesis requieren es seguir el flujo de sicarios desde i a j (centrípeta) o desde j hacia i (centrífuga) para explicar el contagio de municipios j a municipios i. Ambas hipótesis trabajan con el mismo conjunto de municipios i y j, la dirección del contagio de los homicidios es distinta, según la dirección del flujo de sicarios, que pretendemos mapear a través de los AOM. Además, las hipótesis plantean mecanismos distintos. En el caso de la hipótesis centrífuga, el contagio obedece a la invasión y la conquista (Lessing 2015). En el caso de la hipótesis centrípeta, es más bien un caso de difusión (Elkins y Simmons 2005): una interdependencia no coordinada. Los agentes en los diferentes municipios se observan entre sí, y reaccionan a lo que ocurre en su entorno mediante un reajuste estructural interno, de manera que el resultado de las incursiones en otros territorios altera el equilibrio militar local, creando incentivos para el conflicto. En este marco, nuestro objetivo no es explicar el patrón espacial, sino determinar cuál de las dos hipótesis cuenta con mayor soporte empírico.
Metodología
Datos
El estudio se basa en los datos de mortalidad publicados por el Instituto Nacional de Estadística y Geografía (INEGI). En México, los registros de mortalidad son generados por las Oficialías del Registro Civil, los Servicios Médicos Forenses, las Fiscalías y las Agencias del Ministerio Público (INEGI 2022). A través del Subsistema de Información Demográfica y Social, INEGI a) recopila estos registros, b) los clasifica y c) los coteja con la Secretaría de Salud (SSA) para asignar a cada caso un tipo de muerte (INEGI 2016).
En cada caso, la presunción del tipo de defunción se origina en el motivo de la lesión, que es registrado por un médico en el certificado de defunción. Todas las causas de muerte se asocian a una categoría de la Clasificación Estadística Internacional de Enfermedades y Problemas Relacionados con la Salud Décima Revisión (OPS 1995). De este modo, INEGI distingue las muertes como homicidios cuando no se deben a eventos ambientales, sino a agresiones: como envenenamientos, disparos, traumatismos, ahorcamientos o agresiones de otro tipo. La clasificación se ratifica o rectifica durante el cotejo con la SSA.
Aquí analizamos los casos que INEGI ya clasificó y publicó como homicidios, y nos enfocamos en aquellos cometidos con armas de fuego o explosivos. De manera adicional, los registros contienen información sobre el año de la defunción, el lugar de la defunción, y el lugar donde la víctima residía. Cuando el municipio de residencia no es igual al municipio en que ocurrió el homicidio, hablamos de personas AOM.
Nuestro universo de estudio lo conforman los homicidios que fueron cometidos con arma de fuego o explosivos, y que ocurrieron entre 2016 y 2022, por ser este el periodo donde se registra el aumento de los AOM; nuestra unidad de análisis es el municipio. Las unidades de observación son los 2471 municipios que conforman el territorio nacional.
Este trabajo se construye a partir de dos variables: el número de homicidios registrados por municipio en un año, y el número de personas asesinadas en otra entidad. Esta variable, a su vez, se crea con las variables municipio de residencia y municipio donde ocurrió el deceso.
La variable dependiente es entonces el número de homicidios en un municipio, y la variable independiente es el número de homicidios en los municipios conectados por relaciones de vecindad definidas por los AOM. Como control, utilizamos el número de homicidios en el año anterior. Todas las variables han sido transformadas a su logaritmo +1.
Sobre la unidad de análisis
Se ha destacado con mucha frecuencia que la actividad criminal no respeta fronteras (Wong 2004). La consecuencia de ello es que todo estudio que parta de unidades geográficas prestablecidas introducirá un sesgo en sus estimaciones. Si bien ello es cierto, no necesariamente aplica igual para toda clase delitos.
Sostenemos que el municipio es una unidad de análisis adecuada cuando se trata de dinámicas de crimen organizado. Esto se debe a que los GCO tienen acuerdos con autoridades locales, y tales acuerdos regulan su propia conducta (Trejo y Ley 2022). Ya en 2011 Fernando Escalante Gonzalbo (2011, 50) escribía: “La policía municipal, corrupta, ineficiente y abusiva como puede ser, tiene que organizar los mercados informales y los mercados ilegales. Se dirá que eso significa complicidad con los delincuentes: es verdad y es trivial”. También Blazquez y Le Cour Grandmaison (2021) han mostrado que las fronteras internas sustentan las modalidades de acumulación de actores locales.
Los municipios fungen como enclaves geográficos donde actores locales pueden fungir como intermediarios entre los GCO locales y poderes externos, y de esta manera administrar los accesos, el tráfico y los contactos políticos. En este marco, la violencia se usa para asegurar una posición de intermediario político, y el municipio se convierte en la unidad geográfica de administración de la violencia. Si los grupos criminales y las autoridades en un municipio están estructuralmente acoplados (Luhmann 2007), entonces el municipio es una unidad de análisis adecuada.
Procedimientos
El objetivo de este trabajo es poner a prueba dos hipótesis sobre la asociación entre los homicidios ocurridos en un municipio y los homicidios ocurridos en otro. Cuando se trata de evaluar el grado de asociación espacial entre dos regiones respecto a una variable de interés, dos técnicas son comunes: los coeficientes de autocorrelación i de moran y los modelos de regresión espacial sustantiva.
Análisis espacial
La autocorrelación espacial se refiere a la relación estadística entre observaciones en diferentes ubicaciones. El coeficiente de autocorrelación espacial I de Moran mide en qué grado el valor de una variable y en la región i está asociado con el valor de la misma variable y en la región j (Vilalta 2005); es decir, indica el grado en que yi es función de yj. El coeficiente puede tomar valores entre 1 (concentración total) y -1 (dispersión total), donde 0 indica la falta de asociación espacial. El coeficiente se obtiene mediante la expresión:
El componente crítico de esta fórmula es la matriz de pesos espaciales, representada por W. Cada elemento wij de la matriz W indica qué unidad espacial puede ejercer influencia sobre otra y con qué intensidad. El uso común es considerar que, si la unidad j es vecina de la unidad i, wij toma el valor de 1, y si no, toma el valor de cero. Luego, el peso se estandariza por filas, dividiendo 1 entre la suma de wij en i. El coeficiente I de Moran indica si hay patrones de concentración o dispersión estadísticamente significativos, pero no nos dice dónde están. Por ello, en el análisis exploratorio de datos espaciales (ESDA), un paso adicional implica analizar los indicadores locales de asociación espacial (LISA): estos muestran cómo cada unidad espacial contribuye al patrón global (Anselin 1995).
El modelo de regresión espacial sustantiva, por su parte, es una forma de modelar la influencia social a través del espacio. El modelo multivariado toma la forma:
En este modelo, el valor de la variable y se explica por tres componentes: a) la influencia del valor de y en los vecinos (definidos, como antes, por W), que toma un coeficiente 𝜌; b) la influencia de factores locales x, que toma un coeficiente 𝛽, y c) un término de error aleatorio 𝜖. En este modelo, las relaciones espaciales son sustantivas, lo que significa que tienen importancia desde el punto de vista teórico.
En su forma estándar, estos modelos conciben la vecindad como colindancia (en el caso de polígonos) o proximidad (en el caso de puntos), y asignan a todos los vecinos el mismo peso. Esto ignora relaciones especiales entre las regiones. El uso acrítico del modelo omite la discusión acerca de los mecanismos que producen el patrón espacial y sus consecuencias empíricas. En cambio, un ejercicio dirigido por la teoría requiere identificar el proceso por el que la influencia entre regiones ocurre, y determinar qué unidades serán tratadas como vecinos (Tita y Radil 2011). De este modo, un modelo de regresión espacial pone a prueba teorías sobre la influencia social en el espacio (Leenders 2002).
En este orden, la tarea más importante en el análisis espacial consiste en especificar la matriz de pesos espaciales W. Al indicar los mecanismos de la interdependencia, W refleja la forma como las unidades se conectan y el proceso espacial que las vincula (Franzese y Hays 2008): W representa la teoría (Leenders 2002). Diferentes maneras de especificar de W indican distintos mecanismos de influencia y llevan a diferentes resultados empíricos.
Según Leenders (2002), especificar la estructura de W implica cuatro pasos:
Decidir si la influencia social ocurre a través de la autocorrelación de la variable dependiente (regresión espacial sustantiva) o de la autocorrelación de las perturbaciones.
Decidir cuál es el mecanismo que gobierna esta influencia.
Decidir, para cada unidad, cuáles otras unidades ejercen influencia sobre ella y cuáles no.
Decidir cuánta influencia ejerce cada una de estas unidades. Cada entrada wij en la matriz W indica la influencia que la entidad j tiene en la entidad i.
Matrices modificadas con el flujo de personas AOM
En este artículo intentamos decidir cuál de las dos hipótesis rivales, la centrípeta y la centrífuga, tiene mayor soporte empírico. Ponemos a prueba la hipótesis según la cual el número de personas AOM constituye el vector o vehículo por el que el número de homicidios en una entidad afecta al número de homicidios en otra entidad. Esto puede implicar dos hipótesis opuestas:
H1 El número de homicidios en la zona de origen de los AOM afecta al número de homicidios en el destino: hipótesis centrífuga.
H2 El número de homicidios en la zona de destino de los AOM afecta al número de homicidios en la zona de origen: hipótesis centrípeta.
Se trata de dos relaciones distintas y de tipo asimétrico (Leenders 2002), porque el flujo de personas AOM es distinto en cada caso. Cada hipótesis implica una matriz W diferente, donde las relaciones de vecindad V son asimétricas, irreflexivas e intransitivas.
W 1 Hipótesis centrífuga
En el primer caso, asumimos que el número de homicidios en la región de origen (j) de las personas AOM influencia el número de homicidios en la región de destino (i). En tal caso, definimos como vecino (V) de i a toda entidad j de la que provenga (L) al menos una persona (x) muerta (M) en i.
Cada j es vecino de aquellos i a los que envía grupos armados. Cada i tiene como vecinos a los j, de donde provienen las personas asesinadas.
En este caso, el peso de cada vecino se decide como función del número de personas AOM muertas en la entidad i y del total de personas AOM originarias de j.
Esto enfatiza la influencia de la región de origen sobre la región de destino (Leenders 2002).
En este caso, el flujo de los AOM y el del contagio del homicidio doloso van en la misma dirección, de j hacia i.
W 2 Hipótesis centrípeta
En el segundo caso, si alguien de i muere en j, entonces j es vecino de i, y el número de homicidios en j afecta a los homicidios en i. Esto sucede porque, al participar los AOM de i en los conflictos en j, el resultado de los enfrentamientos en j afecta el balance de poder en i. En tal caso, definimos como vecino (V) de i a toda entidad j en la que muera (M) al menos una persona (x) residente en (L) en i.
Cada unidad espacial j es vecina de aquellas unidades i de las que provienen las personas AOM que fallecen en j. Por su parte, cada unidad i tiene como vecinos a aquellos j donde ocurren las muertes de los AOM. En este contexto, el flujo de AOM se dirige de i a j, mientras que el contagio de homicidios se produce en sentido opuesto, de j a i. Esta dinámica se explica porque, desde la unidad i, una organización invade la unidad j, y el resultado del conflicto en j afecta el equilibrio militar en i. Por lo tanto, la violencia en j desencadena violencia en i, no debido a una invasión como en la hipótesis centrífuga, sino a un ajuste interno entre los grupos en i.
En este caso, el peso de cada vecino se decide como función del número de personas AOM muertas en la entidad j pero originadas en i, y del total de personas AOM que mueren en i.
Esto enfatiza la influencia que la región de destino acepta de la región de origen (Leenders 2002). En W1, si en un municipio i no muere nadie proveniente de otros lugares, entonces existe al menos un municipio de destino i que no tiene vecinos. En W2, si hay un municipio i que no tiene muertos en otras entidades, entonces ese municipio i no tiene vecinos. En ambos casos se cumple que:
En tales casos, el valor de la variable de rezago espacial es cero. Esto se conoce como la zero policy, que permite observaciones sin vecinos (Pebesma y Bivand 2023).
Controles
Nuestra estrategia consiste en comparar los estadísticos de autocorrelación espacial i de Moran, y los coeficientes de modelos de regresión espacial, considerando tres tipos de matrices de pesos espaciales: una matriz W0, sin modificar, contra las matrices W1 (hipótesis centrífuga) y W2 (hipótesis centrípeta) antes descritas. Comparamos estos resultados en siete periodos, en los años que van de 2016 a 2022.
En el caso de los modelos de regresión espacial, como variable de control se incluye el número de homicidios en i en el periodo anterior. Esta variable constituye un control adecuado, en la medida en que captura todas las otras variables locales que afecten al número de homicidios en ese municipio. La variable de tratamiento es el logaritmo del número de homicidios en las entidades vecinas, de acuerdo con las definiciones de vecindad W 0 , W 1 y W 2 .
Aparato
Todos los procedimientos indicados se realizan en R, mediante las librerías sf, spdep y spatialreg.
Resultados y discusión
En esta sección presentamos los resultados del análisis sobre el logaritmo del número de homicidios.
Autocorrelación espacial
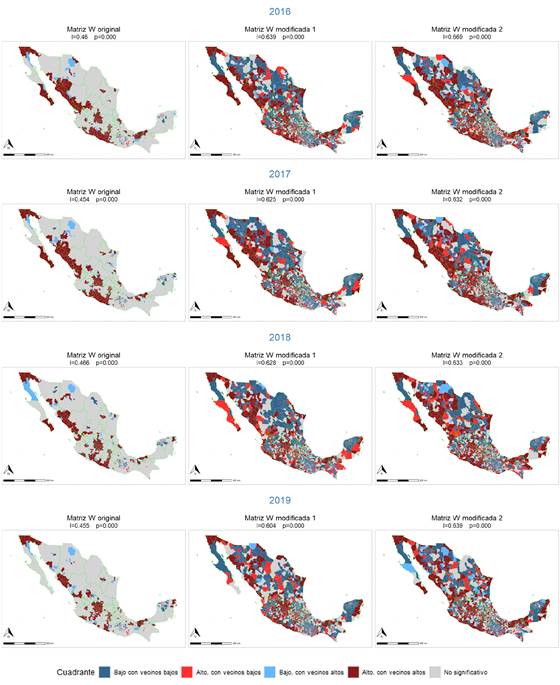
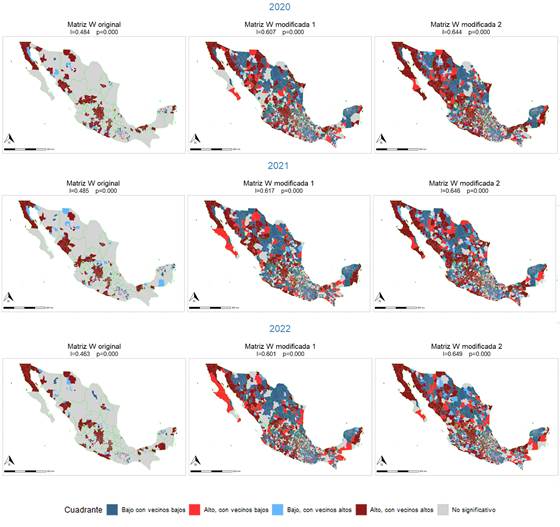
El análisis LISA se efectuó de manera separada para cada una de nuestras matrices de pesos espaciales ( 𝑊 0 , 𝑊 1 y 𝑊 2 ) y para cada periodo. Los resultados se muestran en los mapas 1 y 2.
En todos los casos se observa interacción espacial: el número de homicidios en los lugares i están asociados con el número de homicidios en los lugares j. Esto es válido (p <0.001) para cada periodo y para las tres formas de definir la relación de vecindad. Además, los resultados indican que la interacción es más fuerte cuando se utilizan matrices modificadas por el flujo de personas AOM en contraste con la matriz W estándar, que a) solo considera como vecinas a las entidades colindantes, y b) asigna el mismo peso a todos los vecinos.
Los coeficientes i de Moran son muy similares cuando se calculan con las matrices 𝑊 1 y 𝑊 2 . Las hipótesis centrífuga y centrípeta representan mejor la realidad que la matriz W0. Sin embargo, es importante destacar que el patrón espacial resultante en cada caso es diferente. Esto sugiere que la influencia del flujo de personas AOM afecta a la dinámica espacial de los homicidios de manera única en cada situación. Es posible que la variación en los patrones espaciales refleje diferencias en los mecanismos de difusión o en los factores locales que influyen en la relación entre los lugares i y j.
Los indicadores locales de asociación espacial clasifican a cada municipio en una de cinco categorías. En rojo oscuro, municipios con muchos homicidios que están conectados con municipios que también tienen muchos homicidios, de acuerdo con alguna de nuestras definiciones de vecindad, W 0 , W 1 o W 2 . En azul oscuro, figuran municipios con pocos homicidios, vinculados con municipios que también tienen pocos homicidios. Entre unos y otros se encuentran dos tipos de anomalías: en rojo claro, municipios con muchos homicidios, conectados con municipios con pocos homicidios, es decir, que no contagian; en azul claro, municipios con pocos homicidios, conectados con municipios con muchos homicidios, es decir, municipios que han escapado al contagio. En gris figuran los municipios que no forman parte de ningún patrón espacial reconocible.
En cada caso, las relaciones de vecindad están definidas por la matriz de pesos espaciales W. En W 0 , la conexión es por contigüidad espacial. En W 1 , es la hipótesis centrífuga: son municipios con muchos homicidios, invadidos por municipios con muchos homicidios. En W 2 es la hipótesis centrípeta: municipios con muchos homicidios, que reaccionan a los muchos homicidios en otras zonas a las que enviaron grupos armados.
La presencia de personas AOM indica relaciones de vecindad no contiguas ni simétricas, en las que el contagio de homicidios es más fuerte. Esto respalda la idea de que considerar el flujo de personas entre lugares mejora la captura de patrones espaciales. Los AOM pueden actuar como vehículos a través de los cuales los eventos en un lugar afectan a otros.
Regresión espacial
Donde el índice de Moran revela patrones espaciales, la regresión espacial se utiliza para evaluar el impacto de estos patrones. La regresión examina cómo las relaciones de vecindad y los factores no espaciales afectan a los valores de la variable dependiente.
En esta sección analizamos los modelos de regresión realizados para cada periodo, con las tres matrices de pesos espaciales. Los resultados se detallan en las tablas 1, 2 y 3.
Tabla 1 Modelos de regresión espacial con matrices W0, W1 y W2 (2016-2018)
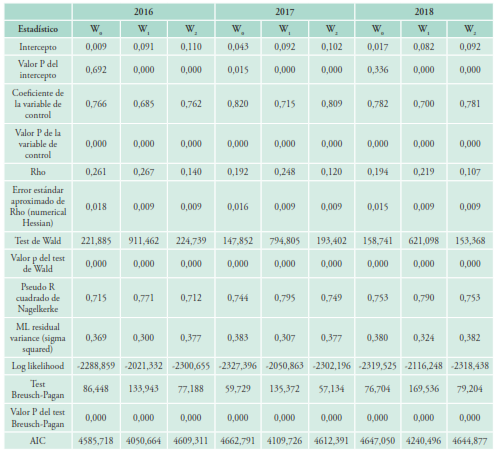
Fuente: elaboración propia con base en INEGI, Defunciones registradas.
Tabla 2 Modelos de regresión espacial con matrices W0, W1 y W2 (2019-2021)
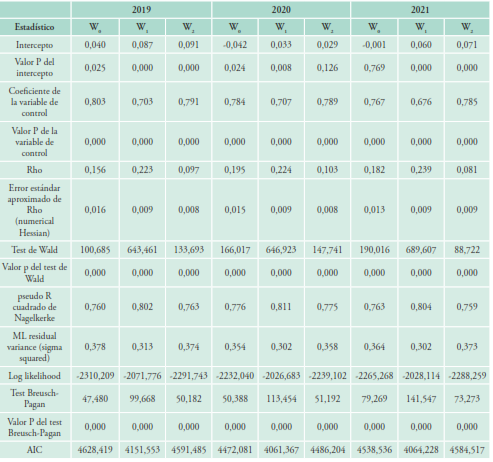
Fuente: elaboración propia con base en INEGI, Defunciones registradas.
Tabla 3 Modelos de regresión espacial con matrices W0, W1 y W2 (2022)
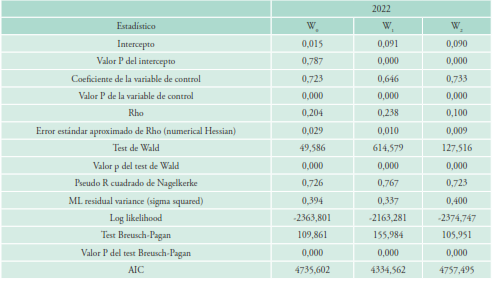
Fuente: elaboración propia con base en INEGI, Defunciones registradas.
Los homicidios en las regiones vecinas j juegan un papel en la explicación del número de homicidios en cada región i. En todos nuestros modelos, el coeficiente 𝜌 asociado al rezago espacial es significativo y positivo. El coeficiente alcanza sus valores más altos en los modelos creados con la matriz 𝑊 1 , esto es, cuando el contagio y los AOM van en la misma dirección (hipótesis centrífuga). En todos los casos, el coeficiente alcanza su valor más bajo con la matriz 𝑊 2 (hipótesis centrípeta), cuando el contagio y los AOM se mueven en direcciones opuestas.
En cada año, el modelo que mejor se ajusta al número de homicidios es el creado con la matriz 𝑊 1 , como muestran los superiores 𝑅 2 de Nagelkerke y Log likelihood, y los menores valores del AIC y de la varianza residual. El peor ajuste corresponde a los modelos 𝑊 2 , que tienen los valores menores en el 𝑅 2 y mayores AIC (excepto en 2017 y 2018).
La variable de control, constituida por el número de homicidios en la misma región, pero en el periodo anterior, es significativa y positiva en todos los casos, además de contar con el coeficiente más importante. Sin embargo, el valor de este coeficiente es menor en los modelos 𝑊 1 .
De esto se sigue que los modelos 𝑊 1 son superiores a los modelos 𝑊 0 , que a su vez son superiores a los modelos 𝑊 2 . Sin embargo, todos los modelos muestran heterocedasticidad, lo que indica que la estructura espacial no ha sido del todo capturada por estas variables. Existe un remanente de heterogeneidad espacial que no se explica por la interacción entre municipios, pero tampoco por sus características no espaciales. El estadístico Breusch-Pagan alcanza sus valores más altos en los modelos 𝑊 1 , lo que indica que estos modelos hacen un pobre trabajo capturando esta heterogeneidad espacial; en cambio, los modelos 𝑊 2 la capturan mejor en varios casos (2016, 2017, 2021, 2022).
En resumen, los resultados revelan patrones significativos de autocorrelación espacial en el número de homicidios, destacando la influencia del flujo de personas AOM en la dinámica espacial. La interacción entre regiones vecinas, en especial si el contagio y los AOM van en la misma dirección (matriz 𝑊 1 ), se presenta como un factor de peso en la explicación de los homicidios, lo que es consistente con la hipótesis centrífuga. Los modelos W 1 tienen un mejor ajuste. Tienen los mayores valores de 𝑅 2 de Nagelkerke y Log likelihood, así como los menores valores en AIC y varianza residual, en contraste con las matrices 𝑊 0 y 𝑊 2 .
Estos hallazgos subrayan la importancia de incorporar el flujo de personas AOM en los modelos espaciales, y dan cuenta de su papel como vectores para la propagación de homicidios entre regiones. Aunque los modelos 𝑊 1 se destacan como los más efectivos, se sugiere cautela, debido a la presencia de heterocedasticidad. La relevancia teórica de estos hallazgos se discutirá en la siguiente sección.
Conclusiones
En este trabajo nos propusimos identificar cuál, entre la hipótesis centrífuga y la hipótesis centrípeta, explicaba mejor los patrones de contagio del homicidio doloso entre los municipios de México, entre 2016 y 2022. Para ello, modificamos las matrices de pesos espaciales: definimos las relaciones de vecindad a partir de los patrones de personas AOM, que simulan el flujo de sicarios consistente con cada hipótesis. Al hacer esto, la matriz W refleja la teoría. En la hipótesis centrífuga, los AOM surgen de la región de origen del contagio; en la hipótesis centrípeta, llegan a ella. Con las matrices modificadas, realizamos pruebas de interacción espacial y modelos de regresión espacial sustantiva para cada año, y los comparamos con los resultados de una matriz W sin modificar. Las pruebas mostraron una fuerte tendencia de los homicidios a concentrarse; esta tendencia es más fuerte en las hipótesis centrípeta y centrífuga que en la matriz sin modificar. En los modelos de regresión espacial, tras controlar para los homicidios en periodos previos, la hipótesis centrífuga resulta superior.
Nuestros resultados son consistentes con las hipótesis de Dell (2015) y de Lopez-Cruz y Torrens (2023). La hipótesis centrípeta (Osorio 2015) no resulta falseada, pero su poder explicativo es bastante menor. Los patrones de contagio del homicidio doloso en México obedecen más a la relocalización y diversificación de las actividades delictivas que al cambio en el balance de poder local ocasionado por la intervención en otros territorios.
Sin embargo, nuestra estrategia metodológica no permite comparar de manera simultánea las dos hipótesis, debido a que hasta ahora no es posible incluir dos matrices de pesos espaciales distintas en un solo modelo de regresión espacial. No sabemos si ambas hipótesis pueden coexistir o si la varianza explicada por una quedaría capturada por la otra. Además, la falta de una varianza constante indica que hay factores no explorados que contribuyen a explicar los patrones espaciales de homicidios. Futuros estudios se beneficiarán de tomar en cuenta la heterogeneidad del espacio.
Nuestros resultados apuntan hacia la naturaleza sistémica del conflicto. Que los homicidios se expliquen por los homicidios, en el tiempo y en el espacio, como muestra la relevancia de estos en el periodo anterior y la autocorrelación espacial, es evidencia de que el conflicto (y no solo los carteles) es un sistema autorreferencial, limitado por la voluntad de las partes, pero cuyo desarrollo no puede ser dirigido por ellas (Luhmann 2007). Como todo conflicto, se trata de un sistema parásito: se alimenta de los recursos que los involucrados pueden movilizar. Por ello, la hipótesis centrífuga resulta más importante que la centrípeta: el sistema-conflicto requiere la multiplicación de los recursos para continuar, y para cumplir este imperativo funcional puede modificar su estructura y su geografía, y sustituir a sus miembros. Pero ninguna de las partes puede alterar unilateralmente su destino. Si la pretensión de aprovechar la debilidad del adversario funciona, es solo un accidente. Subrayamos la necesidad de abordar estas cuestiones desde una perspectiva sistémica.
Un problema secundario emerge del seguimiento de los AOM. Si una persona es asesinada en un estado diferente al de su residencia, se considera un problema del estado donde ocurre la muerte, y se incluye en la estadística de dicho estado. Sin embargo, el origen del problema reside en el estado donde esa persona fue reclutada. Todo lo que facilita el reclutamiento de futuros AOM convierte las condiciones de vida en una entidad federativa en una amenaza para la seguridad de otra entidad federativa.
De este modo, algunos estados pueden considerarse un “oasis de seguridad” mientras contribuyen a la inseguridad en otras regiones. Nuestros hallazgos subrayan la naturaleza sistémica de la seguridad pública y, como corolario, la necesidad de que los beneficios globales se logren a través de inversiones locales. No solo es crucial identificar los destinos más probables de la relocalización de grupos criminales, dado el mecanismo centrífugo, sino también abordar las condiciones que favorecen el reclutamiento.
Estos hallazgos son relevantes en la medida en que amplían nuestra capacidad para explicar cómo se propagan y se perpetúan los conflictos criminales en México. Este estudio permite identificar conexiones asimétricas que van más allá de la mera contigüidad espacial, implicando que el proceso de contagio es altamente selectivo; además, este trabajo permite poner a prueba y refinar las hipótesis centrípeta y centrífuga, señalando que la ciencia política del crimen gana más, en materia de prevención, analizando las oportunidades criminales que pueden complementar los ingresos de las organizaciones, que los intentos de adivinar y capitalizar la debilidad de los adversarios. Por último, este trabajo hace progresar la teoría, al mostrar que las guerras de conquista pueden involucrar a regiones muy distantes, lo que hace que la geografía de las guerras criminales sea dinámica y cambiante, susceptible de transformarse por completo en unos pocos años.