1. INTRODUCCIÓN
La minimización irrestricta desempeña un papel crucial en la Zona Vis, especialmente en la optimización de sistemas de energía integrados híbridos que combinan fuentes de energía eólica, solar y térmica. En este contexto, se utiliza para ajustar los parámetros del sistema y maximizar la producción de energía mientras se minimizan los costos operativos (Cox et al., 2023). Además, es fundamental en la extracción precisa de parámetros de modelos fotovoltaicos (Farag et al., 2023), lo que mejora la capacidad de prever el rendimiento de los sistemas fotovoltaicos en diversas condiciones (Paixão et al., 2023). En este trabajo, planteamos el método de minimización irrestricta de una función espectral no lineal de restricciones de desigualdad basada en mediciones de radiación Vis y un modelo de transferencia de radiación Vis, para calcular el coeficiente de turbidez atmosférica por aerosoles de la zona Vis.
Antecedentes
Debido a la naturaleza computacional de la resolución de problemas de minimización, se revisaron los métodos iterativos: descenso de gradiente, Newton-Raphson y el gradiente conjugado de Fletcher-Reeves para la optimización sin restricciones utilizando dos funciones que pertenecen a una clase de funciones de Rosenbrock (Aliyeva et al., 2022). Para resolver los problemas de programación cuadrática (QPP), se propuso un lagrangiano implícito para la clasificación a través de un problema de minimización convexo sin restricciones. Las soluciones a las variables duales se obtienen utilizando esquemas iterativos de enfoques de aproximación suave que contienen funciones no diferenciables (Emiola & Adem, 2021).
Si la función objetivo no es cercana a una cuadrática, la dirección de búsqueda es generada por un modelo cónico bajo condiciones apropiadas que posee la propiedad de descenso suficiente en el que la dirección de búsqueda es calculada minimizando un modelo aproximado seleccionado en un subespacio bidimensional (Borah & Gupta, 2020). La tasa de convergencia del subespacio gradiente de rango constante obtiene convergencia más rápida mediante un parámetro que controla el decaimiento de la norma de gradiente para funciones convexas y de Lipschitz, en comparación a versiones conocidas de descenso de gradiente ruidoso (estocástico) (Li et al., 2019).
La formulación de un problema de optimización sin restricciones tiene como objetivo minimizar la probabilidad de interrupción en las comunicaciones bidireccionales, con respecto a la ubicación del relé y asignación de tiempo para la recolección de energía. Además, se observa como la tasa objetivo de transmisión influye en la probabilidad de interrupción y eficiencia espectral del sistema de comunicación que utiliza el protocolo híbrido de retransmisión de conmutación de potencia y tiempo (Kairouz et al., 2020). Un problema de minimización sin restricciones "diferenciable" (problema de mínimos cuadrados) está asociado con un sistema de ecuaciones no lineales, con función objetivo, basada en la norma, y resuelta mediante la minimización de la suma de los cuadrados de los residuos. Asimismo, subgradientes iterativos de la función objetivo es calculada mediante problemas de minimización sin restricciones, para la resolución de los problemas asociados (Ghosh et al., 2019).
Cuando la restricción de la función objetivo en el camino de búsqueda proyectada no es diferenciable. Se proponen los métodos de conjunto activo de aproximación cuasi-Newton y de punto interior primal dual para la búsqueda de línea cuasi-Wolfe sustancialmente eficiente y confiable (Stefanov, 2021).
La zona Vis es de vital importancia en la búsqueda de material fototérmico rentable, el diseño de una tela de almacenamiento solar visible, logra una alta eficiencia energética de liberación de calor (83 °C) de aproximadamente 4,8% bajo la luz solar, lo que puede proteger el cuerpo humano de lesiones por frío causadas por un brazalete autocalentable (Fei et al., 2021). En la región Vis 430 ~ 627 THz, un metamaterial absorbente (MA) muestra una absortividad superior al 80%, mejorando la eficiencia de las células solares, esto debido a la movilidad de fotones significativos de conversión y absorción que pueden integrarse a la tecnología de células solares (Hoque & Islam, 2020).
A causa de la región visible, el espectro polarímetro visible del Telescopio Solar Daniel K. Inouye (DKIST) es capaz de observar regiones solares de hasta un área de 120×78 arcsec2 dentro del rango de 380 a 900 nm del espectro solar, lo que permite realizar estudios espectro polarimétricos bien establecidos de la estructura magnética y la dinámica del plasma de la atmósfera solar, así como investigaciones completamente novedosas del espectro solar (de Wijn et al., 2022). En la teledetección satelital, el trayecto de un rayo de radiación Vis desde el Sol hasta el objetivo (superficies terrestres o marinas) y el sensor se ven fuertemente afectados por la presencia de la atmósfera (Basith et al., 2019).
Para desarrollar un modelo de zona de banda ancha Vis, es necesario herramientas de medición para recopilar datos y técnicas de modelado para simulaciones de la radiación de longitudes de onda larga (Di Pietro, 2022). Sin embargo, debido a las incertidumbres de sus cálculos se necesitan saber sobre cómo los cambios de Vis afectarían a los seres humanos y ecosistemas. El modelo de atenuación de los componentes: rojo, verde y azul (RGB) de la radiación solar Vís, determinó que los coeficientes de atenuación promedio tienden a la unidad en el rango, desde la dispersión de Rayleigh hasta la dispersión de la luz en una niebla intensa de una atmósfera contaminada (Aliyeva, et al., 2022). La naturaleza estocástica de la radiación solar Vis hace que esta sea difícil de modelar dificultando su fiabilidad mediante una metodología robusta y fácil de usar para simular Vis se podría determinar un modelo solar capaz de evaluar un sistema de energía integrado con energía solar (Abunima et al., 2019).
Por otro parte, un buen conocimiento del parámetro de atenuación de la radiación Vis, turbidez atmosférica por aerosoles permitió explicar la histórica erupción volcánica del Monte Pinatubo (1991), el Niño (1998), un evento de humo de biomasa sin precedentes (1998) y la Niña que causó la sequía más severa registrada en la historia de Texas (2011) (Mims, 2022).
Importancia de la Minimización Irrestricta
El método de minimización irrestricta de funciones es fundamental en numerosas áreas de investigación y aplicación como el diseño de dispositivos fototérmicos avanzados, la minimización de costos (Upadhyay et al., 2019), detección de objetos en un entorno sin restricciones, minimización de circuitos (Ilango et al., 2020), diseño óptimo de un cuantificador polar no restringido (Wu & Dumitrescu, 2020), el problema de ubicación de instalaciones distribuidas (Filos-Ratsikas et al., 2023), aprendizaje de clasificadores de la Red de Markov (MN) sin restricciones (Franc et al., 2021), sistema de estacionamiento que hace que el movimiento de los vehículos en movimiento sea irrestricto (Manoharan et al., 2021), informática distribuida (Drozdowski & Shakhlevich, 2021), el problema de ubicar instalaciones desagradables (Alamatsaz et al., 2021), etc.
Relación de la minimización irrestricta y la Zona Vis: Aplicaciones y Relevancia
Los métodos de minimización irrestricta permiten hacer visible información oculta en los datos de condiciones óptimas, lo que posibilita así una mejor comprensión y manipulación de los sistemas fotovoltaicos (PV) (Duan et al., 2023). La zona Vis representa el rango de parámetros y condiciones en el que se puede operar eficazmente un PV, mientras que la minimización irrestricta permite explorar y optimizar este espacio de manera eficiente.
Se propone la aplicación de un algoritmo novedoso y eficiente, basado en el flujo turbulento de optimización a base de agua para resolver problemas de flujo de potencia óptimo en redes de energía con energía solar fotovoltaica y unidades de turbina eólica. La minimización irrestricta juega un papel importante en la determinación de las configuraciones óptimas de la red de energía, mientras que la Zona Vis se refiere a las restricciones y consideraciones sobre la generación de energía solar y eólica en ubicaciones específicas (Alghamdi, 2023).
La extracción de parámetros de modelos fotovoltaicos presenta algoritmos de optimización avanzados. La minimización irrestricta se aplica en la búsqueda de los parámetros óptimos del modelo, mientras que la Zona Vis influye en la generación de datos de entrada del modelo, como la irradiancia solar y la velocidad del viento (Eslami et al., 2022).
El desarrollo de un modelo de programación para optimizar la energía de una concentración de energía solar de un sistema fotovoltaico (PV). La minimización irrestricta se utiliza para maximizar las ganancias y determinar un calendario de energía rentable, mientras que la Zona Vis se refiere a las fluctuaciones en la disponibilidad de energía solar y eólica a lo largo del tiempo (Hamilton et al., 2020).
La propuesta de un modelo de soporte vectorial no lineal con una función de penalización estricta para pronosticar la radiación solar. Aquí, la minimización irrestricta se aplica en la optimización de los parámetros del modelo para mejorar la precisión del pronóstico, mientras que la Zona Vis se refiere a la variabilidad en la radiación solar, influenciada por factores meteorológicos (Jiang & Dong, 2016).
Estos estudios demuestran la importancia de considerar tanto los aspectos de optimización como las características específicas del entorno, como la disponibilidad de recursos solares y eólicos, en el diseño y la operación de sistemas de energía renovable.
2. MATERIALES Y MÉTODOS
Modelo de transferencia de la zona Vis
El modelo físico de intensidad de radiación Vis (i ( ) en (Wm-2µm-1) para longitudes de onda (() en la zona 0,445 µm ((( 0,610 µm atenuada que llega directamente a la superficie de la Tierra, considera rayos monocromáticos extraterrestres (i o ) en (Wm-2µm-1) incidentes sobre la atmósfera alta, que varían debido a que esta capa está compuesta de aerosoles, ozono y vapor de agua distribuidos irregularmente en todo su volumen, produciendo efectos simultáneos combinados de transmitancias independientes (vea la Ecuación 1) de dispersión Rayleigh (t r ), absorción por ozono (t o ), aerosoles (t a ) y vapor de agua (t w( ) (Lisenko, 2018).
i ( ((,l,(,w)=(r/r o )2 i (o (()t (r t (o t (a t (w (1)
Donde:
r o =1.496x108 km, es la distancia media Sol-Tierra, r es el radio de órbita elíptica de la Tierra alrededor del Sol, en uno de sus focos (Stutzmann & Csoklich, 2022) y d es el número del día,
(r/r o )2=[1+0.033cos(2(d/365)]2. (2)
La masa de aire relativa m r , en función del ángulo cenital solar ( z en grados (Bai & Zong, 2021) es:
m r =[cos( z +0.15(93,885-( z )-1.253]-1 (Bosca Berga, 1995). (3)
La masa de ozono m o , en función de la altura h o =22 km donde se da la máxima concentración de ozono es:
m o =[(1+h o 6370-1)/(cos 2 ( z +2h o 6370-1)0,5]. (4)
La masa de aire m a , en función de la presión estándar P o =1,013 mb y la presión local P en mb,
m a =m r P/P o (Lefèvre et al., 2013). (5)
Además,
t (r ((,m a )=exp(-m a /[(4(115,641-1,335(-2)]), (6)
es llamada dispersión Rayleigh (Gueymard & Kambezidis, 2004),
t (o (k (o ,l,m o )=exp(-k (o lm o ) (Zo et al., 2014), (7)
siendo k (o el coeficiente de absorción de ozono en cm-1, l el espesor de ozono en cm,
t (a ((,(,m a )=exp(-( -( (,m a ) (Costa et al., 2012), (8)
siendo ( el coeficiente de turbidez por aerosoles sin unidades, (=102,74x10-2 para (<0,5 µm y (=1,206 para (>0,5 µm, k a( el coeficiente de absorción por aerosoles dada en cm-1,
t (w (w,k (w ,m r )=exp[-23,85x10-2 wk (w m r /(1+20,07wk (w m r )0,45] (9)
siendo w el vapor de agua precipitable en cm y k (w el coeficiente de absorción de vapor de agua sin unidades (Iqbal, 1983).
Tipo de atmósfera
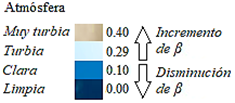
Podemos clasificar a la atmósfera de acuerdo con la cantidad de pequeñas partículas sólidas o líquidas suspendidas en el aire cuyos tamaños están comprendidos entre 0,002 y 100 µm de radio, pueden ser de procedencia terrestre (humos, polen, cenizas de erupciones volcánicas, incendios forestales, combustión de carbón, polvo, arena de tormentas, etc.) o de procedencia marina (cristales de sal, núcleos de sales higroscópicas en los que condensa el agua, aerosoles oceánicos) (Zakinyan & Zakinyan, 2023) y su distribución es determinada por el valor de ( como muestra la Figura 1.
Datos de investigación
Este trabajo fue realizado en los laboratorios del Departamento Académico de Ciencias Básicas de la Universidad Nacional José María Arguedas en Andahuaylas del Perú en condiciones reguladas.
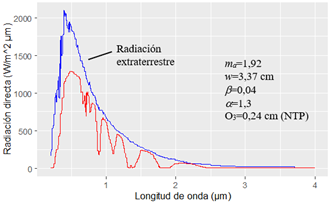
Figura 2 Banda espectral solar extraterrestre i (o e incidente directa atenuada i (e sobre la superficie terrestre (Wright, 2003)
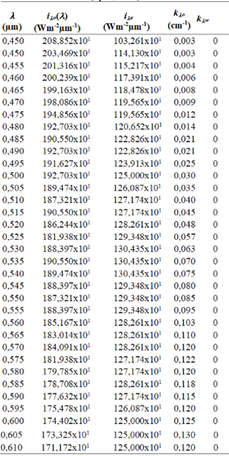
La metodología de investigación empleó el método cuantitativo, con una muestra de 34 intensidades de la zona Vis (ver la Tabla 1), obtenida a partir de la técnica documental mediante el Software Paint a través del espectro de radiación directa (ver la Figura 2) registrado con el pirheliómetro Eppley de incidencia normal. La medición se realizó al aire libre, en el área del Departamento de Física de la Universidad Heredia, el 20 de Agosto del 2002, bajo condiciones de cielo despejado e iluminación de sol directa. Durante la medición, la temperatura osciló entre 20 y 40 grados Celsius, sensibilidad 8 mV/m2, impedancia 200 (, linealidad (0.5% de 0 a 2,800x103 W/m2 (Wright, 2003).
Modelo matemático
Planteamos el problema de optimización, definido como ξ: (3(( con región de factibilidad ϑ={a((3} (Ferry et al., 2021).
ξ(a)=Σ([ℋ(a)-1]2 (10)
a((3.
Donde ℋ(a)=i ( ((,a)/i (e sin unidades, siendo a=[a 1 a 2 a 3]t=[l ( w]t.
La Ecuación 10 es la función a minimizar y corresponde al problema de minimización sin restricciones.
A partir de la Tabla 1, se puede observar que k (w =0 para la zona Vis, se sustituye ese valor. En la Ecuación 9 se obtiene:
t (w (w,(0),m r )=exp[-0,2385w(0)m r /(1+20,07w(0)m r )0,45], (11)
entonces,
t (w (w,(0),m r )=1, (12)
reemplazando la Ecuación 12 en la Ecuación 1 obtenemos,
i ( ((,l,()=(r/r o )2 i (o (()t (r ((,m a )t (o (k (o ,l,m o )t (a ((,(,m a ), (13)
esta ecuación reduce un grado de libertad en la Ecuación 10, se obtiene:
ξ(a)=Σ([ℋ(a)-1]2 (14)
a((2.
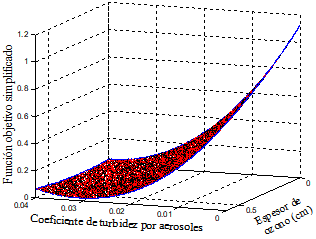
Con a=[a 1 a 2]t=[l (]t, queda la función objetivo simplificada a ξ: (2(( con región de factibilidad ϑ={ a((2} (Dwail & Shiker, 2020).
Cuando se obtiene un minimizador local a * de la Ecuación 14, la diferencia entre los valores de i ( ((,a) y i (e se minimiza.
Una estrategia para resolver el problema de optimización sin restricciones es:
Paso 1: Resuelva el sistema de ecuaciones
grad ξ(a)=0, (15)
y obtenga una solución a * .
Paso 2: Verificar si la matriz hessiana es a * es definida positiva, es decir hessian ξ(a)>0. Si fuera el caso, entonces a * es un minimizador local estricto del problema de optimización.
Esta estrategia puede ser implementada en un programa en Matlab 19.0 mediante el Algoritmo básico con corrección de Armijo usando backtracking, dado de la forma:
Sean (((0,1(, a (k) y d (k) , tal que
grad ξ(a (k) ) t d (k) <0, (16)
definir (=1.
Mientras
ξ(a (k) + ( (k) d (k) )>ξ(a (k) )+( ( (k) grad ξ(a (k) ) t d (k) , (17)
escoger (([0,1(; 0,9(], caso contrario, definir ( (k) =(
hacer a (k+1) =a (k) +( (k) d (k) .
Consideraciones y limitaciones del método de minimización irrestricta
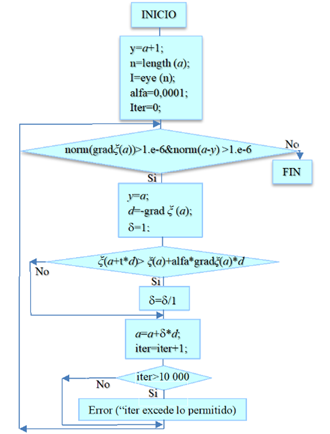
La estrategia algoritmo básico con corrección de Armijo usando backtracking para la minimización irrestricta puede converger a mínimos locales a * en lugar de mínimo global deseado, especialmente en funciones no convexas (ver la Ecuación 14). Además, son sensibles a las condiciones iniciales y pueden experimentar convergencia lenta, especialmente en problemas de alta dimensionalidad (grados de libertad). Requieren derivadas de la función objetivo (ver la Ecuación 16) y pueden ser computacionalmente costosos (ver la Figura 3), además de ser sensibles a la escala de las variables a y los criterios de terminación de la iteración (ver la Ecuación 17). La elección del algoritmo adecuado es crucial, ya que algunos pueden ser más robustos que otros frente al ruido o la presencia de múltiples mínimos locales.
Programa en Matlab 19.0
El algoritmo de Armijo implementado en el Software Matlab 19.0 a partir del problema matemático (ver la Ecuación 14) se obtiene un minimizador local a*, este método controla la dirección del vector gradiente que hace que la función objetivo disminuya de modo que ξ siempre sea continua y diferenciable, basado en el diagrama (ver la Figura 3).
Parámetros de incertidumbre de la banda Vis
El error de sesgo medio relativo (rMBE) y error cuadrático medio relativo (rRMSE) (Masoom et al., 2020) de los valores de i ( ((,a) son definidos como:
rMBE=(100/N)(Σ(i (e - i ( ((,a))/i (e,prom ), (18)
rRMSE=(100/i (e,prom )(([(1/N)Σ(i (e - i ( ((,a))2], (19)
donde N es el número de datos.
3. RESULTADOS Y DISCUSIÓN
Resultados
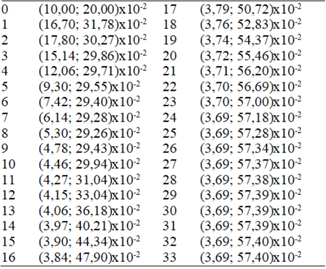
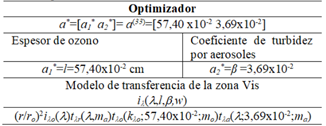
En la Tabla 2, se presenta el optimizador a * de ξ (ver la Ecuación 14) mediante la ejecución del algoritmo Armijo en Matlab 19.0 en 33 iteraciones (ver la Tabla 3).
También, es posible visualizar que los datos del optimizador a * es característica de una atmósfera turbia que no posee adelgazamiento de la capa de ozono de cielo blanco alternado. A partir de los valores de l y β, solo β es preponderante en la zona Vis, esto se debe a que es principalmente atenuada por la presencia de aerosoles.
Tabla 2 Datos obtenidos del programa en Matlab 19.0, para estación del Departamento de Física de la Universidad Heredia
Como la función objetivo simplificada está definida como ξ: (2((, es posible graficarla. Mediante la Figura 4, se puede visualizar que la mínima altura correspondería a l=57,40x10-2 cm y (=3,69x10-2.
Para corroborar esta afirmación mediante la Figura 5, ξ en función de ( mantiene constante el dato optimizado de l. También, se visualiza que la función ξ tiene su menor altura en el rango 0<β<0,05 llamado “restricción”. Nuestro dato optimizado a 2 * se encuentra dentro de ese rango.
Finalmente, deseamos comparar los datos de radiación solar Vis experimental y teórica.
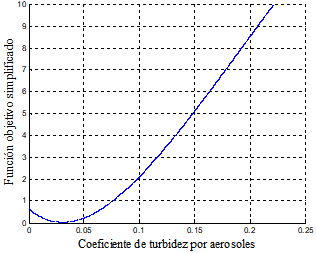
Figura 5 Ilustración de ξ en relación a ( conservando constante l=57,40x10-2 cm utilizando Matlab 19.0
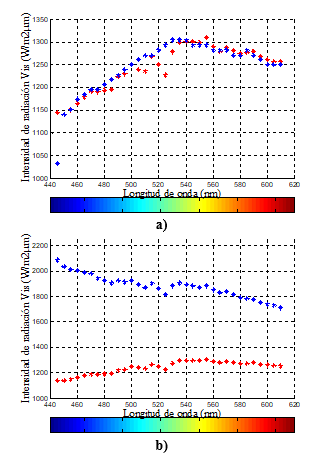
Mediante la Figura 6a, se visualiza que en la zona Vis existe una concordancia entre los datos empíricos y los calculados teóricamente.
La Figura 6b ilustra una visualización comparativa entre los rayos monocromáticos extraterrestres y los calculados teóricamente en la zona Vis. Además, se visualiza que en la zona Vis la i (o directa es atenuada en su trayectoria por: dispersión de moléculas de aire (dispersión Rayleigh), absorción por aerosoles y capa de ozono, en su paso por la atmósfera, llegando i ( a la superficie de la Tierra.
También, mostramos los resultados de los parámetros de incertidumbre del modelo de transferencia de la zona Vis en la Tabla 4. Igualmente, se observa que las incertidumbres son pequeñas, siendo un buen indicativo que el modelo de transferencia de radiación da una buena estimación de la zona Vis.
Discusión
El modelo desarrollado de radiación de la zona Vis, posee las herramientas de medición (Wright, 2003), recopilación de datos (Software Paint) y técnicas de modelado (Di Pietro, 2022) (algoritmo de Armijo). Los cálculos de l,( en Matlab 19.0 permiten saber cómo cambia la radiación Vis, con un sesgo pequeño (Masoom et al., 2020).
El optimizador obtenido por la técnica algoritmo básico con corrección de Armijo usando backtracking, en este trabajo fue un optimizador global. Esto se debe a que mediante la Figura 4, se pudo buscar datos (ver la Tabla 3) dentro de la región de factibilidad del problema de optimización (ver la Ecuación 10), sin embargo, en general no siempre se podrá visualizar la función objetivo, lo que limita a encontrar minimizadores locales.
Los resultados obtenidos a través del enfoque de minimización irrestricta en la optimización de parámetros l, ( del modelo de la función objetivo simplificada en la zona Vis han demostrado ser válidos y robustos en varios aspectos. La validez de los resultados se sustenta en la mejora de la precisión y robustez en la estimación de algunos parámetros del modelo fotovoltaico de Dan (Duan et al., 2023). Esta mejora en la precisión contribuye a una extracción más confiable de los parámetros tanto la zona Vis como de módulos fotovoltaicos, lo que sugiere que el enfoque de minimización irrestricta es efectivo en mejorar la calidad de los resultados obtenidos. Debido a que nuestra función objetivo simplificada tuvo baja dimensionalidad, su convergencia fue rápida en comparación con la de los modelos de Premkumar y Li (Li et al., 2023; Premkumar et al., 2023).
Una posible fuente de error fue la sensibilidad a la escala de las variables l, ( y los criterios del algoritmo de Armijo respecto a la terminación de la iteración, que afectó la convergencia del algoritmo y por ende la precisión de los resultados. El algoritmo de minimización irrestricta pudo ser sensible a las variaciones de las condiciones iniciales provocando soluciones muy diferentes, lo que podría afectar la precisión de la estimación de los parámetros del modelo de la zona Vis.
Se sugiere establecer la técnica de algoritmo de Armijo para el diseño de procesamiento de optimización de datos de la zona Vis, esto puede implicar el uso de sensores, controladores, software y hardware especializado con el fin de lograr resultados más favorables.
CONCLUSIONES
Conforme con los hallazgos obtenidos, se deduce que se logró estimar la Zona Visible mediante el cálculo de modelos: transferencia de la zona Vis, modelo matemático “función objetivo simplificada” y uso de la técnica “algoritmo básico con corrección de Armijo usando backtracking”. Mediante la implementación del algoritmo de Armijo en un programa en el Software Matlab 19.0, se obtuvo un minimizador local a * de una función objetivo sin restricciones. A partir de los datos de minimizador, concluimos que los datos empíricos de radiación de la zona Vis pertenecen a una atmósfera sin agujero de ozono con cielo blanco alternado turbio para la estación del Departamento Académico de la Universidad de Heredia.
La ilustración de ξ en relación con ( permite determinar la restricción del valor del coeficiente de turbidez por aerosoles, el cual podría ser utilizado para el uso del método de optimización con restricciones de desigualdad.