1. INTRODUCCIÓN
Los pozos de caída de vórtice se utilizan habitualmente en los sistemas de alcantarillado urbano para transportar aguas pluviales o residuales a través de grandes desniveles. Un sistema de pozo de caída de vórtice consta básicamente de tres componentes: una estructura de entrada, un pozo vertical y una tubería de salida aguas abajo, que conecta al alcantarillado desde la salida del pozo. El agua baja en espiral por el tubo vertical en forma de remolino regular y la fuerza centrífuga garantiza que el flujo se adhiera a las paredes del pozo, evitando así la caída libre (Del Giudice et al., 2009).
En los últimos 10 años, la dinámica de fluidos computacional (CFD) se ha convertido en una herramienta fundamental para el análisis de estructuras hidráulicas complejas, ya que permite simular de manera precisa y eficiente el desarrollo de los fluidos (Mrope et al., 2021). En este estudio se aplicó CFD para analizar el comportamiento hidráulico del flujo en un disipador de energía tipo vórtice en sistemas de alcantarillado, el cual es utilizado comúnmente en ingeniería para reducir la energía cinética de los flujos en canales abiertos en zonas de mucha pendiente, prevenir la erosión y el socavamiento de las estructuras aguas abajo (Usman et al., 2023).
La simulación numérica en este tipo de estructuras hidráulicas ha tenido mayor apertura en el continente asiático, donde las condiciones topográficas precisan construir disipadores de energía, es así como Chan et al. (2018) en Hong Kong abordaron la incapacidad de los modelos teóricos para explicar el flujo tridimensional (3D) en la entrada de un disipador hidráulico. Para ello, realizaron una simulación numérica en 3D utilizando el método de volumen de un fluido, y así validar sus predicciones con mediciones de velocidad mediante anemometría Doppler láser. Este estudio representa un avance significativo en la comprensión del flujo en 3D en disipadores hidráulicos.
Debido a la complejidad del flujo helicoidal que se produce en el disipador de energía, las mediciones experimentales en toda la estructura representan un desafío significativo, por ello, se utilizó la simulación numérica usando los resultados de un modelo físico a escala realizado por Chiluisa y Guanoluisa (2015), para calibrar y validar la parametrización del modelo numérico. Estos resultados permitieron posteriormente, predecir el comportamiento del prototipo, considerando que es 15 veces más grande que el modelo a escala.
Al existir más de un tipo de disipador tipo vórtice, resulta difícil estandarizar el comportamiento del flujo en la estructura, es así como, investigaciones previas han desarrollado simulaciones de disipadores tipo vórtice con una entrada tangencial a la cámara espiral. Yang et al. (2021) mencionan en su investigación que el núcleo de aire en el conducto vertical denota una clara asimetría. Por el contrario, el disipador tipo scroll estudiado en el presente documento adquiere un comportamiento diferente. Consecuentemente, se ha podido analizar el comportamiento del flujo helicoidal y la disipación de energía en función de la geometría del disipador.
Tomando en cuenta que en un modelo numérico se pueden simular diferentes estructuras hidráulicas y del material que se requiriese, es imperativo considerar valores de rugosidad acorde al material de la estructura. En esta investigación, se han desarrollado simulaciones con material acrílico para el modelo a escala, así como hormigón para el prototipo y tras realizar un análisis de sensibilidad se ha podido concluir que este parámetro puede obviarse tras una correcta configuración de datos iniciales y validar los resultados en función de datos experimentales, con el fin de optimizar el modelo y tiempos de simulación.
El análisis de los resultados obtenidos en la simulación numérica del prototipo permitirá una comprensión más profunda del comportamiento hidráulico del disipador de energía en un flujo estacionario y su aplicación en el diseño hidráulico. Esto debido a la versatilidad que ofrece CFD con la generación de diversos escenarios, por lo que este estudio servirá como una base para futuros diseños de disipadores de energía (Ogunsesan et al., 2021).
2. METODOLOGÍA
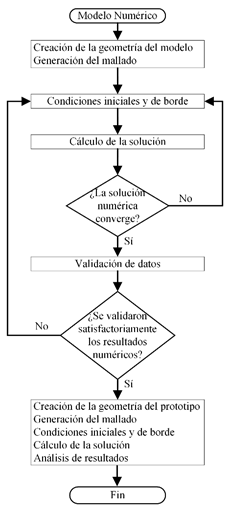
El diagrama de flujo de la Figura 1 describe el proceso del trabajo.
Creación de la geometría
La simulación numérica se ha llevado a cabo partiendo de la creación de la geometría del disipador tipo vórtice mediante Solidworks Student 2023 (SolidWorks, 2023), para esto ha sido necesario remitirse a los planos realizados por Chiluisa y Guanoluisa (2015).
Mallado de la geometría
La discretización del dominio computacional del disipador tipo vórtice se ha generado a través de un mallado mixto combinando elementos hexaédricos (malla estructurada) y tetraédricos (malla no estructurada) según se recomienda en Yang et al. (2021). Las zonas que poseen cambios de dirección y secciones variadas en donde la malla no estructurada se encuentra en la cámara espiral, conducto vertical y cámara de disipación. Además, se ha realizado el refinamiento cuatro veces más pequeño de la malla en las aristas y cambios de sección del disipador.
En relación con la discretización del dominio computacional, también se llevó a cabo un análisis de independencia mediante la realización de cinco escenarios con diferentes tamaños de celdas. El escenario que cumple con la calidad de mallado, parametrización de calidad de ANSYS CFX (Ansys, 2023) y con la calibración de resultados tiene las siguientes características: tamaño de celda de 0.01m, un total de 307 766 nodos y 4h16minutos de simulación. En relación con los parámetros del mallado óptimo, se han obtenido los siguientes valores: 0.25 para la oblicuidad, 0.83 para la ortogonalidad, 2.03 para el aspecto del elemento y 0.94 para la calidad del elemento.
Se ha considerado la limitante de nodos que se pueden utilizar en el programa en su versión estudiantil (512 000 nodos). Además, las características del computador utilizado fueron: 16 GB de memoria RAM, SSD de 512 GB y un procesador Core i7 de 12ª generación.
Condiciones de borde
Una vez definida la malla óptima mostrada en la sección anterior, se procede a la parametrización de las características físicas del modelo, es decir, datos climáticos en las que fueron determinadas las características hidráulicas del modelo físico, las fronteras de ingreso y salida del flujo, paredes de la estructura, la frontera en contacto con la presión atmosférica.
El tipo de modelo de turbulencia escogido en primera instancia fue el RANS (Reynolds-Averaged Navier-Stokes), principalmente por razones de eficiencia temporal, ya que este modelo promedia las ecuaciones de Navier-Stokes en el tiempo o en el espacio eliminando fluctuaciones a pequeña escala. Generalmente, el modelo RANS permite realizar simulaciones más eficientes, en conjunto con modelos adicionales para capturar los efectos de la turbulencia. Por otro lado, el modelo DNS (Direct Numerical Simulation) realiza un proceso de resolución de las ecuaciones de Navier Stokes sin aproximaciones, lo que permite soluciones precisas a costa de una alta demanda computacional (Ruiz Solorio, 2014).
Entre los modelos RANS de turbulencia disponibles en ANSYS (Ansys, 2023), se escogieron dos, según criterios de simulación de estructuras similares propuestos por Yang et al. (2021) y Rodríguez (2016) que son: k - ε y RNG k - ε. El primero de ellos idealiza dos parámetros: la energía cinética turbulenta (k) y la tasa de disipación de energía turbulenta (ε), mientras el modelo RNG k - ε se basa en el modelo k- ε, incorporando los efectos de escala de la turbulencia por lo que se utiliza para simular flujos en un rango más amplio de escalas.
Estos autores sugieren que el modelo RNG k - ε se acopla adecuadamente a un disipador tipo vórtice pues denota una mejor predicción del flujo de chorro en un análisis estacionario. Por otro lado, con el modelo k - ε se puede resolver gran cantidad de flujos turbulentos pues denota una gran solidez matemática y baja demanda computacional. Es por ello que el modelo k - ε ha sido utilizado mayormente para simular flujos industriales, así como modelos en los que intervenga transferencia de calor.
La simulación numérica se realizó con ambos modelos, adquiriendo un comportamiento muy similar y con resultados que confieren aceptabilidad en ambos casos. No obstante, para la presente investigación se eligió el modelo de turbulencia k - ε, que tardó 4h 16min de simulación, debido a su menor gasto computacional en comparación con el modelo RNG k - ε, que tardó 5h 10min de simulación.
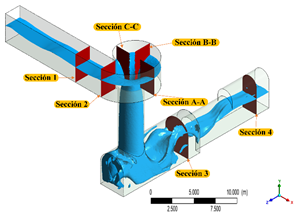
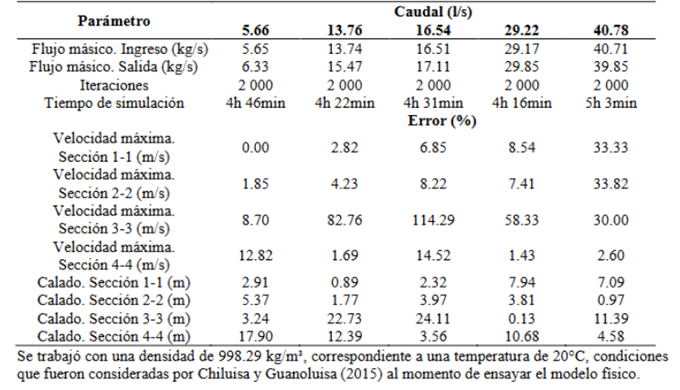
Los datos climáticos usados en el modelo han sido: presión de referencia de 0.71 atm, gravedad de 9.81 m/s2 y temperatura del aire a 20°C. A pesar de que la simulación numérica podría realizarse para cualquier caudal, esta investigación se centra en la simulación de cinco caudales específicos, como lo indica la Tabla 1, utilizados con el propósito de realizar comparaciones con los resultados obtenidos del modelo físico y validar la simulación. Esta comparación se lleva a cabo en cuatro secciones, las cuales se muestran en la Figura 2.
Solucionador
Una vez definidas las condiciones de borde del modelo numérico, se configuran las iteraciones máximas que el programa ejecutará y el valor mínimo de los residuales (RMS). Estos parámetros son establecidos para iniciar el proceso iterativo y obtener una solución aproximada de las ecuaciones de flujo.
La evaluación de los residuales en el modelo numérico indica si aquello está convergiendo hacia una solución precisa y estable, pues si los valores obtenidos son muy grandes denota que la solución no ha convergido y son necesarias más iteraciones para poder lograr una solución aceptable. Para el caso en estudio, se ha determinado un total de 2 000 iteraciones con un umbral de RMS de 1.0x10-4, valor habitual a considerar en estructuras hidráulicas (Fernández, 2011).
En ciertos escenarios, como el abordado en esta investigación, las curvas residuales no alcanzan el umbral de RMS definido. Sin embargo, dichas curvas tienden hacia una misma solución en las últimas iteraciones del proceso, lo que indica que se ha obtenido convergencia en la solución, así como estabilidad en los resultados. Pues, según lo señalado por Fernández (2011), existen varios criterios para validar una simulación numérica, siendo la estabilidad, uno de los más relevantes en modelos influenciados por la turbulencia.
La solución del modelo numérico se validó correctamente al comparar los resultados computacionales con los datos del modelo experimental, como se evidencia en la Tabla 1. Los errores porcentuales, calculados como el valor absoluto de la diferencia entre el resultado del modelo numérico y el valor experimental dividido por el valor experimental, son generalmente aceptables, siendo menores al 10% (Yang et al., 2021).
Los errores que exceden el margen establecido se encuentran en las secciones 1 y 2 de velocidades, para un caudal de 40.78 l/s. Este error refleja la incertidumbre inherente en la recopilación de datos físicos, pues para caudales anteriores, el error es inferior al 10%.
Es crucial destacar que en la sección 3-3, correspondiente a la cámara de disipación, el comportamiento del flujo es variable, por lo que existen errores porcentuales de más del 100%. Esta discrepancia se atribuye a la turbulencia en el disipador, un fenómeno complejo que puede ser desafiante de modelar con precisión.
Con respecto a la sección 4-4, tanto para calados como velocidades, errores mayores al 10% son atribuibles a su proximidad a la cámara de disipación. En esta zona, se produce un flujo mixto de agua y aire, fenómeno que el software puede tener dificultades para simular con precisión, resultando en estas variaciones. A pesar de estas anomalías, los resultados presentados en la Tabla 1 proporcionan una base sólida para avanzar con la simulación y el análisis del prototipo.
3. DISCUSIÓN DE RESULTADOS
Dado que la parametrización del modelo numérico ha sido validada previamente con los resultados del modelo físico, se dispone de la configuración adecuada para simular el disipador de energía tipo vórtice en un escenario distinto. En este caso, se trataría de una geometría de mayor tamaño, equivalente al prototipo. Este enfoque permite la proyección de los resultados obtenidos en la simulación del modelo a escala a un sistema de tamaño real, proporcionando una herramienta valiosa para el diseño y optimización de disipadores de energía tipo vórtice en aplicaciones prácticas.
Para la transposición de las condiciones iniciales de un modelo físico a un prototipo se hace uso de la teoría de la similitud, propuesta por Kline, que menciona: “Si dos sistemas obedecen al mismo grupo de ecuaciones y condiciones gobernantes, y si los valores de todos los parámetros y las condiciones se hacen idénticas, los sistemas deben exhibir comportamientos similares con tal de que exista una solución única para el grupo de ecuaciones y condiciones” (Sotelo, 1974).
Es por ello que esta simulación se la realizará con un caudal de 25.46 m3/s y 35.54 m3/s, que por similitud hidráulica está en correspondencia con el caudal de 29.22 l/s y 40.78 l/s, ya que la relación entre el caudal del modelo y prototipo está establecida con la siguiente fórmula:
Siendo lambda (λ) la relación entre las dimensiones longitudinales del prototipo y el modelo físico.
Es importante destacar que los resultados obtenidos en este estudio están sujetos a cierto grado de incertidumbre, atribuible a diversas fuentes. En primer lugar, el método de Volumen de Fluido (VOF) implementado en el software ANSYS que presenta limitaciones en la simulación precisa del flujo bifásico agua-aire (Yang et al., 2021). Específicamente, puede surgir dificultades al resolver con exactitud las interfaces entre ambos fluidos, un desafío que se intensifica en flujos con alta turbulencia o en presencia de fenómenos complejos como la atomización.
Además, las condiciones ambientales pueden introducir incertidumbre adicional. Un conocimiento insuficiente de los efectos de estas condiciones sobre la medición, o una medición imperfecta de las mismas, puede generar variaciones en los resultados.
Por último, los datos de entrada iniciales, obtenidos a través de mediciones en el disipador, están sujetos a un margen de error inherente. Estos errores pueden propagarse a través del modelo numérico y afectar la precisión de los resultados.
A pesar de estas fuentes de incertidumbre, es relevante señalar que no han impactado de manera significativa los resultados de este estudio, ya que la validación de los resultados ha demostrado ser óptima. Sin embargo, es crucial tener en cuenta estas fuentes de incertidumbre al interpretar los resultados y al aplicar el modelo computacional a prototipos a escala real.
Análisis de sensibilidad
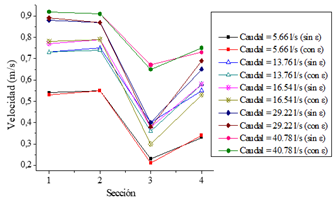
Se llevó a cabo un análisis de sensibilidad para evaluar el efecto de la rugosidad en el modelo físico mediante la simulación de 10 escenarios. El objetivo fue determinar si la rugosidad es un parámetro relevante en la simulación del disipador tipo vórtice y, en caso de no serlo, considerar la posibilidad de prescindir de este parámetro en el prototipo. En la Figura 3, se aprecian los resultados de velocidades en el modelo, el cual se ha configurado con una rugosidad absoluta (ε) de 1.5x10-3 mm (material acrílico) y una configuración omitiendo este parámetro.
Una vez obtenidas las curvas de velocidades, se observa que las diferencias de esta variable son despreciables, con una diferencia máxima de 0.04 m/s. Además, en correspondencia a los cambios de velocidad, los calados variaron 0.02 m. La sección 3 no fue considerada debido a su exposición a la turbulencia desarrollada en la cámara de disipación, lo cual genera datos menos representativos.
Cámara espiral
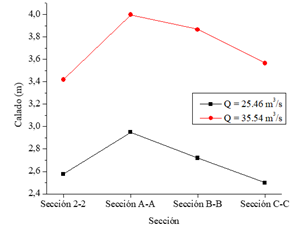
El objetivo de esta sección es guiar el flujo de agua en una trayectoria helicoidal, donde se produce un cambio de calado a lo largo de este recorrido, como se muestra en la Figura 4.
El calado tiende a incrementar en la sección A-A en consecuencia de la fuerza centrífuga generada por el cambio de dirección del flujo. Posterior a esta sección, los calados disminuyen conforme el flujo avanza hasta la entrada al tubo vertical. No obstante, es preciso mencionar que mientras el área mojada que circula en la cámara disminuye, las velocidades adquieren un comportamiento inversamente proporcional.
Este fenómeno guarda similitudes con el flujo en otros tipos de disipadores tipo vórtice, como los circulares, espirales o tangenciales, ya que, a pesar de diferir en su geometría, comparten la misma función: mantener estable el flujo y dirigirlo hacia la entrada del tubo vertical.
Tubo vertical
La zona del tubo vertical contempla una de las partes más importantes del disipador tipo vórtice, y puede ser analizada de manera más eficiente mediante una modelación numérica en comparación con un modelo a escala. Un aspecto importante del movimiento del flujo en esta zona es la presencia de dos componentes de la velocidad; una tangencial (perpendicularmente al eje del tubo vertical) y otra axial (paralela al eje del tubo vertical). En cuanto a la rugosidad del modelo, se la configuró de acuerdo con las propiedades del hormigón, considerando una rugosidad absoluta de 0.36mm. Sin embargo, este parámetro no ejerce una influencia significativa en el desarrollo del modelo como se lo explicó en el apartado de análisis de sensibilidad (Crispino et al., 2021).
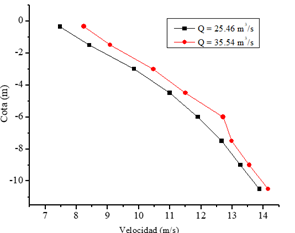
La velocidad que se desarrolla a lo largo del tubo vertical adquiere un crecimiento debido a la acción de la gravedad. La Figura 5 indica las máximas velocidades en cada cota a lo largo del tubo. Así mismo, en esta gráfica solo se ha analizado la velocidad resultante, ya que es la velocidad primordial para el análisis correcto de la estructura hidráulica.
Otra característica importante que proporciona el modelo numérico es la visualización del ángulo de inclinación del flujo, lo cual provee información muy significativa que ayuda a evaluar si la longitud del tubo vertical es adecuada para lograr la formación del flujo helicoidal (Chan et al., 2019).
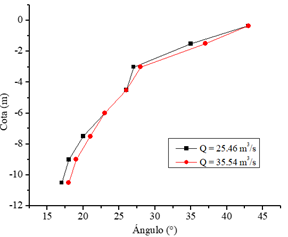
El ángulo de inclinación (θ) se forma con respecto al eje vertical y es de esperarse que conforme el flujo avanza, existirá una variación en el comportamiento del ángulo. En la Figura 6, se puede observar como este ángulo disminuye mientras se acerca a la cámara de disipación, esencialmente debido a la fricción con las paredes y al aumento de la componente axial de la velocidad.
Una observación acertada de este comportamiento es que el vector velocidad coincide con la dirección de las líneas de flujo, como es de esperarse, el cual se puede medir en ANSYS obteniéndose valores importantes para realizar cálculos analíticos.
Con respecto a la longitud máxima que el tubo vertical puede poseer, es importante mencionar el trabajo de Hager (1985), quién presentó una fórmula para estimar esta longitud, en la cual la velocidad tangencial disminuye su magnitud, dejando de tener un impacto significativo en la resultante de velocidad lo cual provoca que el flujo adquiera un comportamiento vertical. La expresión matemática que describe esta relación es la siguiente:
Donde, K es el inverso del coeficiente de Manning, g es la gravedad, Q es el caudal y D es el diámetro del tubo vertical.
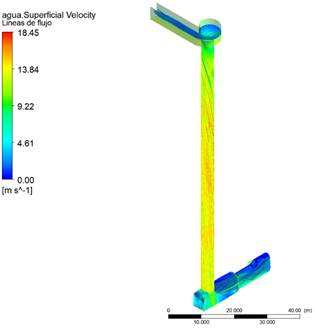
Aplicando la fórmula (1) se han obtenido longitudes máximas en función de los caudales simulados, con lo cual se ha modificado la geometría del tubo vertical y se consiguió visualizar el comportamiento de las líneas de flujo como se aprecia en la Figura 7, lo que confirma la validez de la ecuación para este tipo de disipador de energía y proporciona una referencia de diseño para esta estructura.
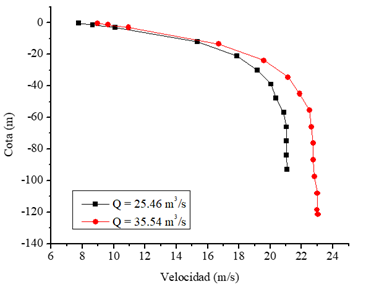
Una de las limitantes que presenta el disipador tipo vórtice en su funcionamiento, es la velocidad máxima con la que puede fluir el agua en el tubo vertical, tal como se puede apreciar en la Figura 8. A medida que el tubo vertical se extiende, se observa que existe una velocidad límite que aumenta en función del caudal que se está desarrollando. Esta velocidad límite es atribuida a la presencia del núcleo de aire en el interior del tubo vertical, el cual genera resistencia al movimiento del flujo (Rodal et al., 2011).
Para el diseño del tubo vertical es necesario considerar una correcta aireación, así como su funcionalidad, para esto se ha hecho uso del valor lambda (λ), mismo que representa la relación entre el área del núcleo de aire y el área de la sección del tubo vertical. Considerando que se recomienda un valor por encima de 0.25, se ha examinado este número a través de la simulación numérica y se ha encontrado que la variación de lambda a lo largo del tubo vertical alcanza un valor mínimo de 0.41, esto garantiza el correcto funcionamiento del prototipo (Chan et al., 2018).
Finalmente, se observaron presiones negativas en la unión del tubo vertical con la cámara de disipación. Para evaluar estas presiones es necesario recurrir al índice de cavitación el cual responde a la siguiente fórmula.
Donde, Pabs es la presión absoluta, PV es la presión de vapor, v es la velocidad y ρ es la densidad del agua.
Un valor superior a 0.2 indica una menor probabilidad de cavitación, como se evidencia para los caudales de 25.46m3/s y 35.54m3/s, cuyos índices de cavitación son: 0.50 y 0.33 respectivamente. Estos valores se deben a las altas velocidades generadas en el extremo del tubo vertical, lo cual resulta en una disminución de la presión (Sentyabov et al., 2016).
Cámara de disipación
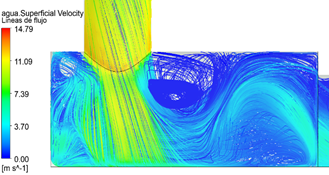
En la Figura 9, se observa el comportamiento del flujo cuando este ingresa a la cámara de disipación, las líneas de flujo adquieren un comportamiento impredecible, así mismo, la velocidad disminuye por presencia de un colchón de agua y como consecuencia se disipa la energía con la que el flujo ha ingresado a la estructura.
Esta sección de la estructura hidráulica presentó el mayor error promedio en comparación con los datos experimentales del modelo físico, donde se identificaron errores de más de 100 %. Esto se debe a la turbulencia generada en esta zona y la complejidad del cálculo con el modelo k - ε, sin embargo, los resultados obtenidos para las demás partes del disipador cumplen con un error aceptable, menor al 10 %, como lo indica la Tabla 1.
El umbral de error del 10% proporciona un equilibrio razonable entre la precisión y la practicidad. En el contexto de la dinámica de fluidos computacional y los modelos hidráulicos, permite una tolerancia en los resultados que no compromete la integridad del modelo.
Además, en el diseño de estructuras hidráulicas, una variación del 10% en los resultados numéricos no suele tener un impacto significativo en las decisiones de diseño ni en el rendimiento final de la estructura. Esto se debe a que los ingenieros a menudo diseñan con un margen de seguridad para acomodar tales variaciones.
Siguiendo con el análisis, las zonas de máxima presión se encuentran en la base de la cámara de disipación, principalmente causadas por el contacto directo del flujo con la solera de la cámara. Aunque esta presión se ve reducida por la presencia del colchón de agua y la generación de turbulencia, esta zona aún estaría expuesta directamente a los efectos de erosión, por lo tanto, deberían evaluarse métodos constructivos para proteger la estructura. Para los caudales simulados de 25.46 m3/s y 35.54 m3/s se obtuvieron presiones máximas de 78 614 Pa y 92 984 Pa, respectivamente.
Para concluir la discusión de resultados, se destaca que, a pesar de las diferencias en las geometrías de los estudios, se observó que las tendencias de las velocidades y calados en el presente estudio muestran una similitud con los resultados de investigaciones previas. En particular, se encontró similitudes con los artículos realizados por Zhang et al. (2018), Yang et al. (2021), Zhao et al. (2006) y Rodríguez (2016). Esta consistencia refuerza la validez de los hallazgos y proporciona una base sólida para futuras investigaciones en este campo.
Limitaciones
Las limitaciones más significativas en la simulación numérica del disipador de energía fueron la discretización y los modelos de turbulencia. Estos factores pueden consumir una cantidad considerable de recursos informáticos durante la ejecución de la simulación si no se definen adecuadamente y el tiempo de simulación puede extenderse a valores que no son prácticos.
La discretización inadecuada puede conducir a errores numéricos que representen de manera imprecisa los fenómenos físicos. Por lo tanto, en este estudio, fue esencial seleccionar cuidadosamente los parámetros de la simulación, donde la limitante del software de 512 000 nodos obligó a trabajar con un número de nodos menor. A pesar de esta limitación, los nodos fueron capaces de captar adecuadamente el comportamiento de los fluidos, lo cual resultó ser satisfactorio.
La falta de una adecuada validación de resultados habría impedido obtener un modelo preciso, puesto que el refinamiento de la malla no se hubiera podido establecer en ANSYS. En tal caso, se puede optar por usar un software libre de simulación, como OpenFoam, donde se permite un mayor refinamiento de la malla y, por lo tanto, una representación más precisa del flujo de fluidos, sobre todo en zonas donde la turbulencia es notoria.
Con respecto a la turbulencia, el modelo k - ε provee una estimación general del comportamiento del flujo dentro de la cámara de disipación y es importante reconocer sus limitaciones. En particular, los modelos RANS proporcionan una descripción promediada en el tiempo del flujo turbulento, pudiéndose no capturar adecuadamente los detalles finos de la turbulencia, como se observó en la cámara de disipación, con errores mayores al 10%.
Para obtener un análisis más detallado y específico del flujo dentro de la cámara, sería beneficioso utilizar un modelo LES (Large eddy simulation), el cual se centra en resolver las estructuras turbulentas más grandes en el flujo, mientras que los efectos de las estructuras más pequeñas se modelan (Capote et al., 2008). Sin embargo, estos modelos requieren una resolución de malla mucho más fina y, por lo tanto, consumen significativamente más recursos computacionales. Aunque el tiempo de simulación con LES puede ser de semanas, este enfoque no se descarta si se dispone de suficientes recursos y tiempo. De hecho, el uso de LES puede ser muy beneficioso para obtener una comprensión más profunda de los fenómenos de flujo complejos.
Es importante tener en cuenta estas consideraciones al seleccionar el modelo de turbulencia más apropiado para una determinada simulación.
4. CONCLUSIONES
El modelo de turbulencia k-ε logró una mejor simulación del comportamiento del flujo en el disipador de energía. Los datos experimentales concordaron de manera adecuada con los resultados del modelo numérico. Además, este modelo de turbulencia demostró ser más eficiente en términos de tiempo de resolución en comparación con el modelo RNG k-ε. Estos hallazgos respaldan la posibilidad de emplear el modelo k-ε en futuros proyectos que involucren flujos con naturaleza helicoidal, así amplían las posibilidades de aplicación en diversos escenarios.
El análisis de sensibilidad realizado en este estudio reveló que la rugosidad de las paredes del disipador de energía tiene un impacto mínimo en los resultados de la simulación. Esta observación crucial sugiere que la exclusión de este parámetro podría simplificar significativamente el modelo. Tal simplificación no solo acelera el proceso de simulación, especialmente en proyectos de gran escala, sino que también reduce notablemente el tiempo requerido para obtener resultados confiables. Lo más importante es que esta optimización se logra sin sacrificar la precisión y la fiabilidad del modelo. Por lo tanto, la exclusión del parámetro de rugosidad podría ser una estrategia valiosa para mejorar la eficiencia de las simulaciones de disipadores de energía tipo vórtice, lo que tiene implicaciones significativas para la modelación y el diseño en la ingeniería hidráulica.
En el proceso de validación del modelo numérico se pudo inferir que la sección 3 incluida en la cámara de disipación, fue la única zona donde no se logró una concordancia con los resultados experimentales, ya que su error excedió el 10 %. Esto trasladado al prototipo solo resalta que los valores en esta región pueden carecer de fiabilidad debido a su comportamiento impredecible. Pero en un enfoque más general, estas zonas continúan demostrando una disipación energética adecuada, dado que la eficiencia de la disipación superó el 80 %.
Al aumentar la altura del tubo vertical, se pudo observar que las velocidades adquieren una tendencia a crecer con forme el flujo circula hacia la cámara de disipación. Sin embargo, esta velocidad llega a un límite donde permanece prácticamente constante debido a la interacción que existe entre el núcleo de aire y las paredes del disipador.
Es crucial garantizar que la longitud del conducto vertical se encuentre dentro del intervalo de la altura máxima. Esto se debe a que longitudes superiores resultarían en la pérdida del comportamiento helicoidal, lo que generaría un movimiento en caída libre. Como consecuencia, se perdería la función original para la cual se diseñó la estructura.