1. INTRODUCCIÓN
La predicción meteorológica de viento como fuente de energía eólica ha desempeñado un papel importante en todo el mundo durante décadas debido a su impacto en la vida humana desde la agricultura (Li et al., 2022), el control de tráfico aéreo (Dönmez et al., 2022), salud (Jastrzebska et al., 2022), desarrollo económico (Zahedi et al., 2022) y seguridad pública (Lesage et al., 2022). Los modelos ARIMA fueron planteados por Box y Jenkins en 1970 en su obra "Análisis de Series Temporales: Pronóstico y Control", la cual muestra que la predicción de viento depende de las características topográficas de la superficie terrestre, donde una serie temporal puede ser inferida a partir de un proceso de generación de datos (Uriel, 1985).
En algunos lugares de África como Tanzania, laderas de Kilimanjaro, centro de Sudán los fuertes vientos transportan la arena a los campos de cultivo secándolas y poniendo en peligro su producción agrícola (Stigter et al., 2002).
El viento es la energía renovable (ER) no contaminante más utilizada en la Unión Europea y constituye una fuente de energía eólica de bajo costo para almacenar energía en los parques eólicos marinos, sin embargo, es vulnerable al cambio climático global, lo cual afecta la vida silvestre y la supervivencia de las especies que dependen de su condición reproductiva personal (Ziemba et al., 2017). Las fluctuaciones de la velocidad del viento son uno de los principales obstáculos para su explotación en la red eléctrica. A una altura de 40 m, la velocidad media del viento en muchas regiones de Libia está entre 6 m/s y 7,5 m/s. A pesar de esto, hay varias épocas del año cuando soplan vientos cálidos y secos en cambio en la región oriental durante un año la velocidad promedio del viento fue 8,21 m/s (Badi et al., 2023).
A partir del siglo XIX, las investigaciones de predicción han aumentado, debido a la disponibilidad de datos meteorológicos online y propuestas de modelos de pronóstico ARIMA (p,d,q) con coeficientes p, d, q (Bórawski et al., 2020; Salman & Kanigoro, 2021).
Las mejoras en la previsión de energía eólica tienen potencial de incrementar la cantidad de reservas necesarias en sistemas con cantidades significativas de energía eólica, y finalmente reducir el costo de la electricidad en dichos sistemas mediante un análisis de series temporales con modelos ARIMA para pronosticar la futura producción de energía eólica con datos históricos (Hodge et al., 2011).
En China, los fuertes vientos produjeron descarrilamiento de ferrocarriles, por ello, se centró en predicción de alta precisión de velocidad de viento para sistemas de alerta de viento de los ferrocarriles. Con ese fin, se utilizó un modelo híbrido que combina la descomposición modal (EMD) y ARIMA mediante el modelo RARIMA (Hui et al., 2015).
Nuevas tecnologías para obtener energía eléctrica a partir de energías renovables llevaron a buscar metodologías que permitan identificar zonas con mejores condiciones de aprovechamiento de energía eólica mediante la utilización de modelos ARIMA aplicados a Tunja (Colombia), y se logró identificar 4 lugares óptimos para ubicar aerogeneradores (Benia et al., 2022; Gómez, 2016). Por ello, la ciencia ha avanzado en los estudios realizados con el fin de conocer las condiciones meteorológicas (temperatura, velocidad de viento, presión atmosférica, humedad, radiación solar, etc.) a través del uso de técnicas como ARIMA, así como el coeficiente U de Theil y el test de Diebold-Mariano (DM) con el que se midió cada una de las técnicas empleadas (Pilco & Acurio, 2019).
La velocidad de viento no solo se utiliza para el diseño e instalación de grandes parques eólicos, sino también para mantener segura la red eléctrica mediante la predicción de velocidad de viento utilizando un modelo estocástico ARIMA y un modelo basado en redes neuronales Feed-Forward Artificial Neural Network (FFANN) o perceptrón multicapa (MLP) (Dumitru & Gligor, 2019).
El uso de datos climáticos de temperatura, precipitación, humedad, horas de sol y velocidad de viento permitieron estimar las próximas 24 horas en un sistema de distribución de agua para riego, a través del uso de métodos ARIMA y redes neuronales (RNCs) (Pulido et al., 2002).
Las predicciones de velocidad de viento tienen profundo interés para el desarrollo de turbinas eólicas y las estrategias para construir grandes parques eólicos, pero estas predicciones se ven afectadas por la turbulencia atmosférica. Por eso, se utilizaron modelos estocásticos de series temporales ARIMA, con datos de 20 meses y una variable gaussiana para modelizar la variable meteorológica de viento (Sim et al., 2018).
La predicción de velocidad de viento a corto plazo, 6-8 horas, para un sistema eléctrico exige cada vez una mejor predicción en el Báltico. Los métodos de análisis de series de tiempo utilizaron modelos ARIMA y sus predicciones se validaron a través del error cuadrático medio de la raíz (RMSE), error porcentual absoluto medio (MAPE) y error absoluto medio (MAE) (Grigonytė & Butkevičiūtė, 2016).
En las islas de Baja California, se pronosticó la velocidad de viento mediante un modelo ARIMA y una red neuronal artificial (ANN), con errores obtenidos para pronosticar la tendencia no lineal que el modelo ARIMA no pudo identificar. Además, se utilizaron los errores estadísticos: MAE, error medio cuadrado (MSE) y RMSE (Cadenas & Rivera, 2010).
En Oaxaca y Metepec, se realizó una comparación de predicción de velocidad de viento entre el modelo ARIMA y modelos autorregresivos no lineales con entrada exógena (NARX), tomando una base de datos de presión, temperatura, viento y radiación solar. Se determinó la influencia de las variables meteorológicas sobre la velocidad del viento. Se concluyó que la red neuronal artificial fue 2,3% mejor que el modelo ARIMA, debido a su carácter no lineal (Cadenas et al., 2016).
Debido a la ausencia de modelos de pronóstico de velocidad de viento en Arequipa, se han producido daños en la agricultura, materiales y pérdidas humanas, por esta razón es necesario hacer un pronóstico mediante un modelo ARIMA. Con este fin, se cuenta con datos de velocidad de viento del Satélite ambiental operativo geoestacionario (GOES), con el propósito de beneficiar al sector de agricultura (aumento de cosechas), porque se encontrará una manera de anticipar las fuertes velocidades de viento. Así también promoverá la elaboración de más modelos estocásticos para futuras investigaciones, no solo en vientos, sino también en precipitación, ozono, presión superficial, radiación solar, etc.
2. MATERIALES Y MÉTODOS
Materiales
La investigación fue realizada en el laboratorio de energías renovables de la Universidad Nacional José María Arguedas (UNAJMA) en ambiente controlado. Para analizar los datos de velocidad de viento de escala longitudinal, se aplicó el método de investigación cuantitativo, mediante el lenguaje de programación R, luego se usó la técnica de recolección de datos y análisis documental para preparar una muestra de 332 datos de velocidad de viento desde el mes de enero hasta noviembre del 2022 del distrito de Socabaya de latitud 16° 27' 9'' Sur y longitud 71° 31' 52'' Oeste. La muestra fue obtenida de la página meteorológica de la NASA consultado en (POWER, 2023). Además, fue tomado en tiempo real por el satélite GOES, el cual está a 35 000 km sobre la Tierra girando en una órbita geoestacionaria para monitorear la población de datos de variables meteorológicas. La serie temporal fue constituida por dos variables una independiente y otra dependiente que son: los días y la velocidad de viento respectivamente.
Tener en cuenta que el tamaño de la muestra afectará la precisión y la confiabilidad de las predicciones realizadas por el modelo ARIMA. Es importante reconocer que, debido al tamaño reducido de la muestra, se cometerán errores estadísticos en las predicciones realizadas por el modelo ARIMA. Estos errores se deben a la falta de datos para capturar completamente la variabilidad y la complejidad del comportamiento del viento en la zona rural de Perú. A pesar de las limitaciones asociadas con el tamaño reducido de la muestra, se considera que el modelo ARIMA proporciona una herramienta valiosa para realizar predicciones preliminares de la velocidad del viento en la zona rural de Perú. Sin embargo, se reconoce la necesidad de recopilar datos adicionales a lo largo del tiempo para mejorar la robustez y la confiabilidad del modelo en futuros análisis.
En este estudio, se utilizan las velocidades de viento a 10 metros sobre la superficie terrestre, proporcionadas por NASA/POWER Nubes y el sistema de energía radiante de la Tierra (CERES) / Análisis retrospectivo de la era moderna para investigación y aplicaciones, versión 2 (MERRA2). Estas mediciones representan la velocidad del viento a una altura estándar y son relevantes para la evaluación de la velocidad del viento encima de la superficie. Los datos utilizados son datos diarios de resolución nativa, lo que significa que representan mediciones diarias de la velocidad del viento a lo largo del año 2022 en la zona rural del Perú, específicamente en el distrito de Socabaya de Arequipa. La elección de los datos diarios se basa en la disponibilidad de los datos proporcionados por NASA/POWER CERES/MERRA2. Además, los datos diarios permiten capturar la variabilidad diaria en las velocidades del viento, lo que es crucial para el objetivo de predecir la velocidad del viento a corto plazo en la zona rural.
Métodos
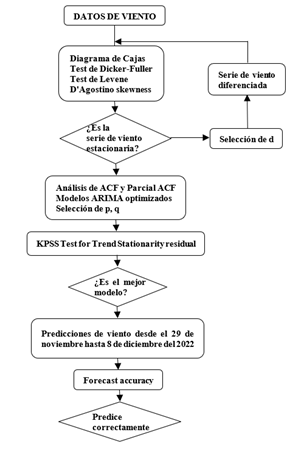
La Figura 1 muestra las fases que se aplicaron para determinar el mejor modelo predictivo.
Las técnicas de análisis de datos aplicadas fueron los métodos paramétricos (Shewhart et al., 2019) en R: diagrama de cajas para la determinación de los valores atípicos, las pruebas de Dicker-Fuller, D'Agostino y Levene para verificación de la estacionariedad y normalidad de los datos antes y después de una diferenciación de orden 1. Además de KPSS Test para la estacionariedad, también se obtuvieron los valores del orden de la parte autorregresiva (p), orden de la parte de media móvil (q) y orden de diferenciación (d) de los modelos ARIMA, donde p representa el número de retrasos o periodos anteriores que se utilizan para predecir el siguiente valor en la serie temporal, q representa el número de términos de media móvil en el modelo, que se utilizan para capturar la estructura de los errores residuales de las predicciones y d indica el número de veces que se diferencia la serie temporal para hacerla estacionaria (Benia et al., 2022).
También, se analizaron los ACF y Parcial ACF para generar los posibles modelos ARIMA, donde ACF es una medida estadística utilizada en el análisis de series temporales para evaluar la autocorrelación entre los valores de una serie temporal y sus valores retrasados en el tiempo. En nuestro estudio, la ACF se utilizó como una herramienta de diagnóstico para explorar la estructura de autocorrelación en los datos de velocidad del viento y guiar la selección de modelos ARIMA adecuados (Sim et al., 2018). Asimismo, mediante ACF e histograma de sus residuales y un proceso de ajuste recursivo AIC y criterio de información bayesiano (BIC) se eligió el mejor modelo. La precisión de la predicción del mejor modelo fue calculada a través de MASE, MAPE y MAE.
Debido al carácter no lineal de la variable meteorológica velocidad de viento, se recomienda utilizar redes neuronales autorregresivas: MLP, NARX, K-vecino más cercano (KNN) ó el método RARIMA, el cual es un modelo mejorado de ARIMA con un funcionamiento análogo al de una red neuronal.
Se recomienda tomar datos de velocidad de viento diaria con equipos del laboratorio de energías renovables de la Universidad Nacional de San Agustín de Arequipa (UNSA) y hacer un contraste con los datos de NASA e implementar otra técnica de predicción para comparar la capacidad predictiva con la de los modelos ARIMA.
3. RESULTADOS Y DISCUSIÓN
Diagnóstico Exploratorio de Datos
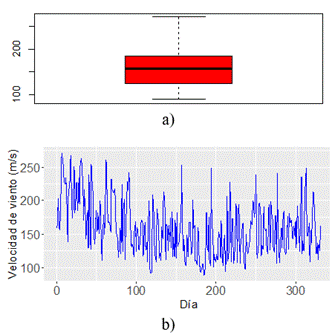
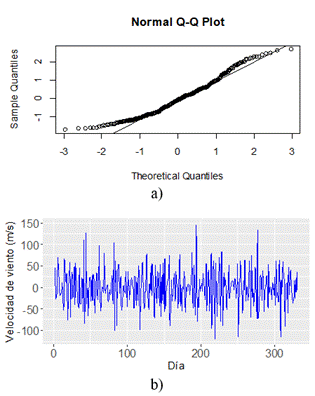
En la Figura 2a, se observa que no hay presencia de valores atípicos para la muestra.
La Figura 2b muestra la serie temporal de la velocidad de viento del año 2022 del distrito de Socabaya-Arequipa. Igualmente, se puede observar un comportamiento caótico debido a la aleatoriedad de la velocidad de viento, por lo que utilizando una simple inspección no se puede predecir el comportamiento de la serie temporal.
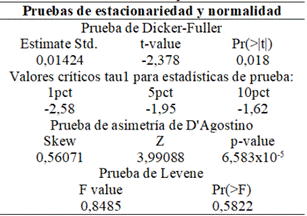
A partir de la Tabla 1 se observa:
Para la Prueba de Dicker-Fuller, t-value -2,378 es menor en términos absolutos a todos los valores de tau, por lo tanto, existe raíz unitaria y la serie no es estacionaria.
Para la Prueba de Levene, la significancia Pr>0,05, por lo tanto, no hay estacionariedad en varianza.
Para la Prueba de asimetría de D'Agostino, la significancia p<0,05. Por lo tanto, la serie temporal no tiene una distribución normal.
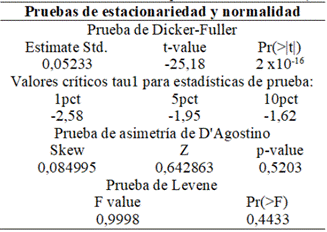
A partir de la Tabla 2 se observa:
Para la Prueba de Dicker-Fuller, t-value -25,18 es mayor en términos absolutos a los valores de tau, por lo tanto, no existe raíz unitaria y la serie es estacionaria.
Para la Prueba de Levene, la significancia Pr>0,05. En consecuencia, hay estacionariedad en varianza.
Para la Prueba de asimetría de D'Agostino, la significancia p>0,05. Por ende, la serie temporal diferenciada tiene una distribución normal.
Según la Figura 3a, se observa que no hay una tendencia a que los puntos de las distribuciones sigan una línea recta. Por lo tanto, la serie temporal no tiene un comportamiento normal.
Para lograr la estacionariedad en media y varianza en los datos de la serie temporal, se diferenció una vez (d=1), como se muestra en la Figura 3b.
Ajuste del modelo
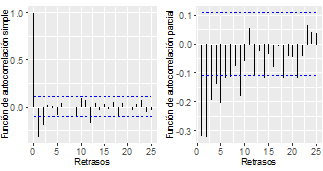
A partir de la Figura 4:
Para la representación gráfica ACF, se observa cuatro retardos significativos, pero solo se tomarán dos retardos debido a que sobresalen más de los límites de confianza obteniendo los modelos de medias móviles (MA), MA(q): MA (1), MA (2).
Para la representación gráfica Parcial ACF, se observa más de tres retardos significativos, se tomarán los dos primeros retardos debido a que sobresalen más de los límites de confianza obteniendo los modelos autorregresivos (AR), AR (p): AR (1), AR (2).
Para el criterio de elección de los retardos, se tomó en cuenta también los valores menores AIC, generados por la función auto.arima de R.
Se obtiene el orden de las partes medias autorregresivas, integradas y móviles del modelo, ARIMA (p d q): (1, 1, 1), (2, 1, 1), (1, 1, 2) (2, 1, 2).
Figura 4. ACF y Parcial ACF para datos de viento diferenciados en R
En la Tabla 3 se presentan modelos ARIMA optimizados mediante un proceso de ajuste recursivo y prueba KPSS.
A partir de la Tabla 3, se pueden observar los modelos con diferentes valores (p,d,q), con su error estimado estándar (Est. Std.), z value obtenidos, varianza de los residuos (σ2), intervalo de confianza entre 2.5 % y 97.5 %, respecto a los coeficientes de los modelos. Se observa que los modelos (1, 1, 2) y (2, 1, 2) tienen valores MLE: -1 638,33, -1 638,32, respectivamente.
En la Tabla 3, también se observa que mediante la prueba Ljung-Box Q de la función Box.test se determina que los residuos del modelo (1,1,2) tienen el valor de p=0.8716> 0,05, mostrando que los residuos no son dependientes y poseen el valor más pequeño del AIC = 3 286,66, además que su intervalo de confianza es el más alto entre 2,5 % y 97,5 %. A partir de la Prueba KPSS el valor p=0,1 >0,05, entonces la serie de tiempo diferenciada es estacionaria en tendencia.
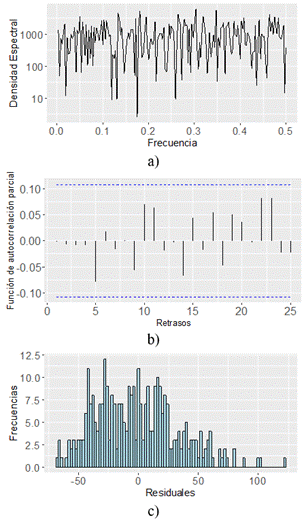
A continuación, analizaremos el comportamiento residual del modelo ARIMA (1, 1, 2).
A partir de la Figura 5, se puede identificar que los ACF de los residuos muestran autocorrelaciones no significativas (vea Figura 5b) y tienen un comportamiento normal respectivamente (ver Figura 5c), y según la gráfica de densidad espectral se verifica que no hay un patrón de residuales (ver Figura 5a), por lo tanto, se puede calcular el pronóstico.
Elección del mejor modelo
La Tabla 4 muestra el mejor modelo obtenido mediante la minimización de la estimación de máxima verosimilitud, AIC, AICc or BIC. Se observa también un ajuste regular para la precisión de predicción logrando el menor error.
Predicción mediante el uso de un modelo ARIMA
La Figura 6 representa el modelo predictivo ARIMA (1,1,2).
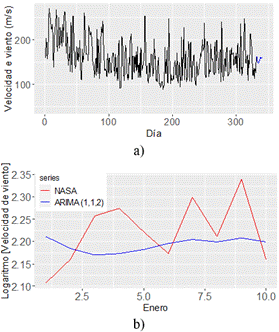
Figura 6 a) Predicción del modelo ARIMA (1, 1, 2), b) Comparación Log [Velocidad de viento] desde 29 de noviembre hasta 8 de diciembre del 2022 en R
La Figura 6a muestra los pronósticos de 10 valores de velocidad de viento futuros de las series temporales desde el 29 de noviembre hasta 8 de diciembre del 2022.
A partir de la Figura 6b, se observa una comparación de los datos de velocidad de viento entre serie temporal del mejor modelo ARIMA (1, 1, 2) y los de la NASA (POWER, 2023).
Discusión
Los datos de viento usados corresponden a varias épocas del año 2022 de la zona rural Socabaya de la región Sur Oeste de Arequipa, cuando soplan con velocidades promedio mayores a 150 m/s (ver Figura 2), a diferencia de las regiones orientales (Badi et al., 2023).
Los datos históricos de velocidades de viento (ver Figura 2) constituyen un potencial para pronosticar la energía eólica fundamental en el desarrollo de turbinas eólicas que podría reducir el costo de la electricidad como los realizados por Hodge et al. (2011) y Pulido et al. (2002).
Debido a la disponibilidad de datos meteorológicos online (POWER, 2023), se pudo proponer el modelo ARIMA (1,1,2) para Socabaya. Esto contribuye al aumento de investigación de predicción como Bórawski et al. (2020) y Salman & Kanigoro (2021).
Los fuertes vientos de Socabaya produjeron accidentes de tránsito, desbordamiento de tierras en las chacras por ello el trabajo se centra en un modelo de predicción ARIMA de buena precisión MASE de 0.849, a diferencia de China que utilizaron un modelo RARIMA (Hui et al., 2015; Pilco & Acurio, 2019).
La predicción de velocidad de viento para Socabaya a corto plazo desde el 29 de noviembre hasta 8 de diciembre del 2022 a diferencia de la predicción, 6-8 horas en el Báltico hecha por Grigonytė & Butkevičiūtė (2016).
En la zona rural de Socabaya, se pronosticó la velocidad del viento mediante un modelo ARIMA (1,1,2) a diferencia de las islas de Baja California, en las cuales, el modelo ARIMA no pudo pronosticar recurriendo a una ANN (Cadenas & Rivera, 2010).
Una limitación del trabajo fue el tamaño de la muestra que delimitó la aplicación de los métodos paramétricos y determinación del mejor modelo ARIMA de la serie temporal.
CONCLUSIONES
Con base en los resultados, se obtuvo el modelo de predicción óptima ARIMA (1, 1, 2) de la serie temporal de velocidad de viento 2022 en R para el Distrito de Socabaya-Arequipa, la cual cumple con las condiciones de estacionariedad en varianza, normalidad, invertibilidad, independencia de residuos y posee menor error.
El modelo ARIMA (1, 1, 2) es viable por su precisión MASE mayor al 0,8 entre datos de velocidad de viento de NASA y los datos pronosticados del modelo. Por lo tanto, el modelo sirve para predecir la velocidad del viento y evitar desastres en la agricultura, accidentes de transportabilidad, así como para mejorar la producción de productos agrícolas, salud, desarrollo económico y seguridad pública del distrito y será preponderante para estudios del cambio climático.
Los procedimientos utilizados en la metodología pueden ser útiles para determinar modelos de predicción de vientos en zonas con altos niveles de velocidades de viento.
No se consideraron los modelos ARIMA (1, 1, 1), (2, 1, 1), (2, 1, 2) para la predicción de velocidad de viento porque sus residuos eran correlacionados, y no se logró obtener el valor más pequeño AIC, además que su intervalo de confianza no es muy alto.
Se ha logrado obtener un modelo de predicción de velocidad de viento que podría estar influenciado por la variabilidad climática (presión, temperatura, radiación solar, etc.)