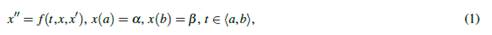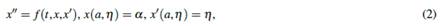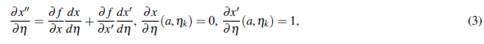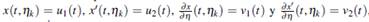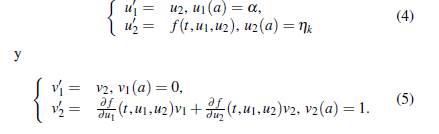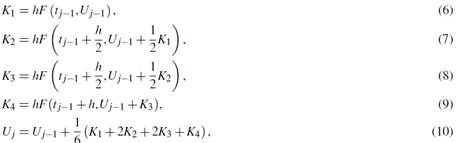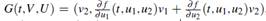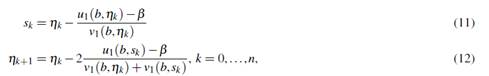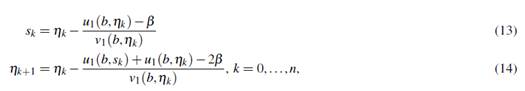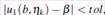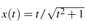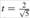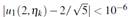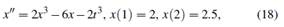INTRODUCCIÓN
El método de disparo es una técnica utilizada para encontrar soluciones de ecuaciones diferenciales ordinarias con valores en la frontera y se efectúa realizando disparos a ciertas velocidades hasta alcanzar el blanco que se sitúa en la frontera. El problema de valores en la frontera (PVF), estudiado por Bailey & Shampine (), está dado de la forma
Este tipo de ecuaciones tiene soluciones analíticas en algunos casos y en otras se hace más tedioso como en el caso no lineal, pero se puede garantizar soluciones únicas implícitas bajo las condiciones suficientes planteadas y demostradas por Schrader (), Ha () y Keller (). Por su parte, () consideran para análisis del problema (1), el problema de valor inicial (PVI) dada por
con η velocidad de disparo y η 0 = (β-α )/(b-a) velocidad de disparo inicial para la parte numérica. La solución exacta x = x(t, η ) de (2) está garantizada por las condiciones mencionadas anteriormente, que son fundamentales para formular la solución numérica del problema (1). En la formulación, la aproximación numérica busca la velocidad de disparo η de mayor precisión, que satisface la ecuación x(b, η ) -β = 0, y esto garantiza una buena aproximación a la solución exacta de (1) en la frontera t = b. Para encontrar velocidades se puede utilizar técnicas iterativas como: bisección, secante, punto fijo, Newton y otros. El rendimiento de estos métodos es diferente, sin embargo la iteración de Newton clásico (NW) es utilizada por muchos investigadores por su rendimiento y ciertas modificaciones como el de (1969). Para sistema diferencial, () aplicaron la técnica de descomposición adomiana y NW en ambos casos en el método de disparo y obtuvieron buenos resultados. Las iteraciones de Runge Kutta de orden 4 (RK4) y de NW pueden ser acopladas al método disparo en la solución de diferentes problemas como de Dirichlet, Sturm-Liouville, Robin y rotación del eje motor (, ; , ; , ; , ).
En los problemas, es difícil obtener en forma explícita la solución del PVF, por lo que se recurre a métodos numéricos como el de Euler, Diferencias finitas, Runge Kutta y entre otros para aproximar a la solución exacta con alta precisión y también se utiliza para describir el comportamiento cualitativo de ciertos modelos relacionados con las ecuaciones diferenciales. El método RK4, propuesto por (), e iteración de Newton clásico serán aplicados a la ecuación (1), en el estudio conjuntamente con Newton modificadas de orden 3. En la presente investigación, se realizó un experimento numérico con método de disparo utilizando RK4 e iteraciones adaptadas de Newton del mismo orden 3, y es aplicado al PVF no lineal () orden 2, con el propósito de determinar la eficiencia de iteraciones adaptadas en la aproximación del PVF. Para obtener resultados numéricos esperados, se utilizó Python 3 por su mayor uso en la actualidad.
MÉTODOS
En la ecuación (2), se deriva con respecto a η y se evalúa en η = η k con (k = 0, . . . , n), se obtiene un nuevo PVI:
donde x ′, denota la derivada con respecto a t.
Considerando
en las ecuaciones 2 y 3 se obtienes las siguientes nuevas ecuaciones
Para obtener solución numérica U j = (u 1(t j , η k ), u 2(t j , η k )), para j≥1, en tiempo t j con velocidad de disparo η k , se aplicó la tabla moderna de RK4 utilizada por () al sistema (4), como sigue
para F (t,U ) = (u 2, f (t, u 1, u 2)), U = (u 1, u 2) y U 0 = (α, η 0). Utilizando
Con V = (v 1, v 2) y V 0 = (0, 1), se obtiene de forma análoga V j = (v 1(t j , η k ), v 2(t j , η k )) por RK4 aplicado a G(t,V ,U j ).
Los resultados obtenidos por RK4 permite obtener las siguientes aproximaciones x(t j , η k ) ≈ u 1(t j , η k ), x ′(t j , η k ) ≈ u 2(t j , η k ) y ∂ x ∂η (t j , η k ) ≈ v1(t j , η k ), y estos son utilizados en NW, para determinar una nueva velocidad de disparo s k y reformulando nuevamente las ecuaciones (4) y (5) para η k = s k , se obtiene nuevas aproximaciones u1(b, s k ) y v1(b, s k ) para velocidad de disparo s k , así sucesivamente hasta lograr aproximación eficiente. Estos valores numéricos obtenidos son asociados a velocidad de disparo η k , y el siguiente paso es buscar velocidades de disparo por iteraciones adaptadas propuestas en la investigación. A continuación, presentamos iteraciones adaptadas de orden 3, de dos pasos con el propósito de construir η1, . . . , η n , a partir de η0.
La iteración Newton orden 3 (NWO3-1), propuesta por (), y al sustituir por u1(b, η k ) y u1(b, s k ) (aproximaciones de x en t = b asociados a las velocidades η k y s k , respectivamente) y, v1(b, η k ) y v1(b, s k ) (son aproximación a ∂ x ∂η (b, η k ) y ∂ x ∂η (b, s k ), respectivamente) quedan adaptadas de la siguiente manera:
donde s k y η k+1 son velocidades de disparo de primer y segundo paso, respectivamente.
La otra perspectiva iteración Newton orden 3 (NWO3-2), dada por (), y utilizando las aproximaciones mencionadas en la iteración anterior, tiene la forma adaptada dada por:
donde s k y η k+1 son velocidades de disparo de primer y segundo paso, respectivamente.
() usan la técnica iteración de orden 3 (NWO3-3), y manera similar como los casos anteriores quedan adaptadas las velocidades de disparo de la siguiente manera:
donde s k y η k+1 son velocidades de disparo de primer y segundo paso, respectivamente.
Estas iteraciones son diferentes pero del mismo orden 3, y fueron demostradas con rigurosidad por los autores mencionados y dichas adaptaciones fueron utilizadas para verificar si las velocidades de disparos encontrados son efectivos. Para la presente investigación, se realizó el experimento con las siguientes iteraciones adaptada de NW, NWO3-1, NWO3-2, NWO3-3 y RK4, en la determinación de velocidades de disparo óptimo con la condición de pare
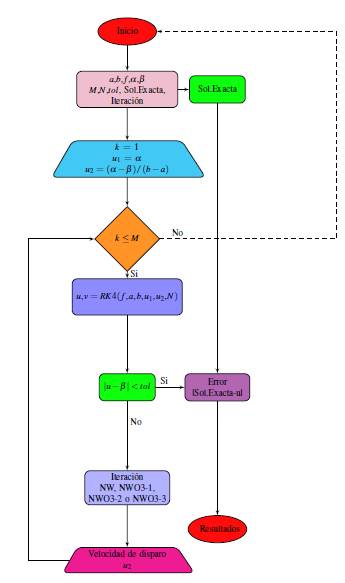
donde tol denota la tolerancia, además se pretende estimar los errores de aproximación a la solución exacta. Asimismo, para la implementación del script del método de disparo se utilizó el diagrama de flujo de la Figura 1 , los paquetes () y (), y se realizó en Python 3, con interfaz Jupyter Notebook.
RESULTADOS Y DISCUSIÓN
El experimento se realizó con la implementación de class Method_diaparo() (ver, apéndices A y B) y los ejemplos:
Ejemplo 1
Considere el problema de valores en la frontera (Filipov et al., 2017):
donde
es solución exacta.
Observe la Tabla 1, los errores de aproximación a la solución exacta en la frontera
generados a diferentes velocidades obtenidas por iteraciones adaptadas. Las iteraciones NWO3-1, NWO3-2 y NWO3-3 se desempeñan con alta precisión que NW. Además, estas iteraciones requieren un promedio 4 o 3 procesos en la estimación; las velocidades finales obtenidas por iteraciones NWO3-2 y NWO3-3 tienen excelentes aproximaciones en la frontera que los demás, como se puede ver en la Figura 2, 1.a), 1.b), 1.c) y 1.d).
Tabla 1 Velocidades de disparo determinados por
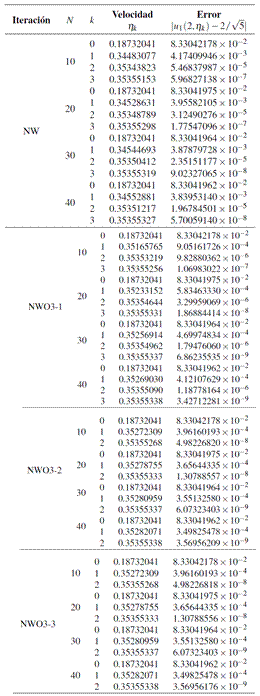
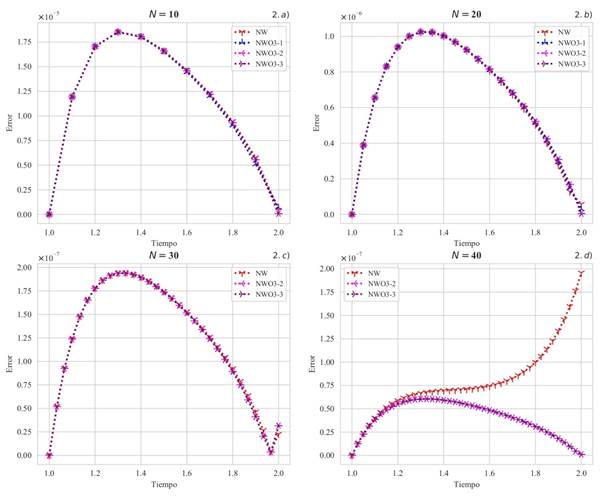

Figura 2 Errores de aproximación a la solución exacta por iteración NW, NWO3-1, NWO3-2 y NWO3-3 a lo largo del intervalo [1,2], para N = 10, 20, 30,40 y a velocidades finales ηk. 1.a), 1.b), 1.c) y 1.d) son errores para el Ejemplo 1 y 2.a), 2.b), 2.c) y 2.d) son errores para el Ejemplo 2
Las iteraciones utilizadas en el Ejemplo 1, a diferentes pasos se obtuvieron de forma satisfactoria las velocidades de disparo y así como sus aproximaciones a la solución exacta. Estos resultados pueden ser replicados a pasos más refinados.
3.2 Ejemplo 2
Sea el problema de valores en la frontera que considera Ha (2001):
cuya solución exacta es x(t) = (t 2 +1)/t.
La iteración NWO3-1 no determina velocidades de disparo para 30 y 40 pasos, debido a la divergencia de la velocidad de disparo y los demás, lo cual permitió alcanzar aproximaciones en la frontera con t = 2.5, ver Tablas 2 y 3.
Tabla 2 Velocidades de disparo determinado por |u1(2,ηk)−2.5| < 10−6, NW y NWO3-1, iniciando η0 = 0.5 en el Ejemplo 2
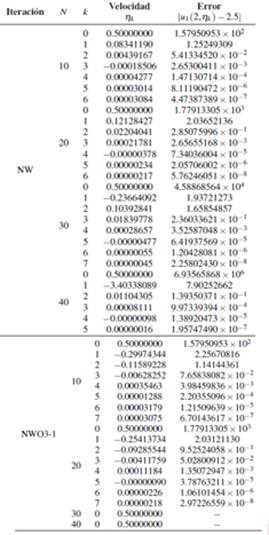
Tabla 3 Velocidades de disparo determinado por |u1(2,ηk)−2.5| < 10−6, NWO3-2 y NWO3-3,, iniciando η0 = 0.5 en el Ejemplo 2
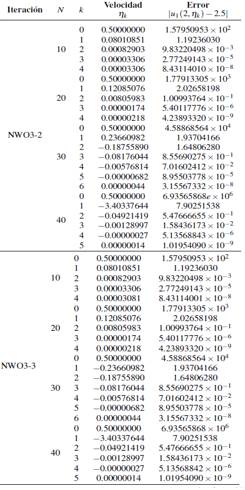
El error mínimo en la frontera para velocidad estimada es 1.01954090×10−9 y se realizó con NWO3-2 y NWO3-3, para N = 40 en el Ejemplo 2 y los demás resultados también son eficaces, pero en menor cantidad de dígitos de precisión ver en las Tablas 2 y 3. Los errores obtenidos por NWO3-1, NWO3-2 y NWO3-3 son menores al resultado obtenido por Ha (2001) y estas iteraciones requieren realizar menor cantidad de operaciones. En la Figura 2, 2.a), 2.b), 2.c) y 2.d), se observan los errores de aproximación a la solución exacta con velocidades estimadas por iteraciones adaptadas. Dentro de los cuales, NWO3-2 y NWO3-3 son precisas en 8 dígitos a la solución exacta en la frontera para N = 20 y N = 40, y en 7 dígitos para N = 10 y N = 30. Sin embargo, las iteraciones NWO3-2 y NWO3-3 son excelentes para aproximar para cualquier paso refinado.
CONCLUSIONES
Las iteraciones NWO3-2, NWO3-3 y RK4 aplicadas al método de disparo son eficientes para aproximar a las soluciones exactas de problemas de valores en la frontera de orden 2. Además, NWO3-1 y NW desempeñan en forma similar y requieren mayor cantidad de procesos que las iteraciones NWO3-2 y NWO3-3.