INTRODUCCIÓN
En la actualidad, el control de una red eléctrica presenta complejidad debido a la cantidad de dispositivos y equipos a ser monitoreados durante su operación. Esta situación de los sistemas eléctricos de potencia (SEP) actuales, requiere del análisis de grandes conjuntos de datos, por medio de los cuales es posible determinar su nivel de estabilidad de pequeña señal, misma que se caracteriza por presentar
modos de oscilación de frecuencias desde 0,1 a 3 Hz. Por lo indicado, dado el volumen de datos es necesario contar con un algoritmo eficiente capaz de trabajar matricialmente para administrar las señales de entrada y salida de los equipos del sistema y dispositivos de control. Estas señales, una vez procesadas adecuadamente, permitirán determinar el nivel de estabilidad presente en el SEP (, ).
En la barra de interés del SEP, es posible obtener las señales de potencia y voltaje, además, si esta barra corresponde a una barra de generación es posible sensar su velocidad. Mediante el análisis modal es posible identificar los modos de oscilación pobre o negativamente amortiguados (, ). Con esta información se puede determinar el nivel de amortiguamiento y oscilatorio del sistema, el cual podría depender de una parametrización incorrecta de los dispositivos de control, entre otras causas ( , ). Dada la dinámica operativa del sistema en búsqueda de mantener el balance entre la generación y la demanda, es necesario que los elementos de control de oscilaciones, como es el caso de los estabilizadores del sistema de potencia (PSS) deben responder a esta dinámica (, ). Así, resulta interesante determinar ante distintos escenarios determinísticos los parámetros de sintonización de los PSS mediante el uso de los residuos de los modos de oscilación críticos como se plantea en este trabajo.
(), () indican que, en la operación y simulación de un sistema eléctrico, el nivel de estabilidad de pequeña señal se determina mediante los modos de oscilación presentes en un escenario operativo del sistema obtenidos principalmente por medio del análisis modal. Generalmente, las oscilaciones se presentan entre los elementos que producen y consumen energía en el sistema. Por lo tanto, surge la necesidad de modelar los elementos de generación y demanda a fin de representar estas dinámicas, a través de un conjunto de ecuaciones algebraicas diferenciales que se resuelven utilizando software de ingeniería. Para el caso del estudio se utiliza PowerFactory, el cual permite obtener el nivel de estabilidad de pequeña señal mediante el módulo de análisis modal.
Mediante el análisis modal de cada condición operativa del sistema, PowerFactory presenta el factor de participación, la frecuencia, el nivel de amortiguamiento y al igual que otros softwares de ingeniería no calcula los residuos (, ).
Para la determinación de los residuos se requiere del procesamiento de la matriz A que contiene el estado del sistema, la matriz C que indica el nivel de observabilidad de las salidas, la matriz B que muestra la controlabilidad de las entradas y los vectores izquierdo y derecho de los modos de oscilación (, ). En el software de ingeniería PowerFactory al ejecutar el comando ComMod* para el análisis modal no se obtienen los residuos (, ; , ). Con esta información, la cual puede ser seleccionada por el usuario en el software, se obtiene el módulo y ángulo del residuo para cada modo de oscilación analizado y con el residuo es posible trasladar el modo de oscilación crítico seleccionado hacia la zona estable mediante la parámetrización del estabilizador de sistema de potencia.
Basado en lo anterior, en este artículo se presenta la programación necesaria que permita la obtención de los residuos de un sistema eléctrico mediante la programación DPL en PowerFactory, por medio del proceso matricial entre las variables obtenidas del análisis modal en combinación con la construcción de las matrices B y C. Estas matrices determinan el nivel de sensibilidad de las variables de entrada y salida y con esta información es posible calcular los residuos de los modos seleccionados. Con el procesamiento de estos últimos se puede desplazar los modos de oscilación críticos al modificar la sintonización del PSS con el fin de incrementar el nivel de estabilidad del sistema de potencia.
Este documento se estructura de la siguiente manera: la sección 2 presenta el análisis modal para el cálculo del residuo, la sección 3 describe algunos aspectos clave para la implementación del script DPL. La sección 4 expone la aplicación de los residuos en la sintonización del PSS para incrementar el nivel de amortiguamiento de las oscilaciones y la sección 5 presenta las conclusiones.
ANÁLISIS MODAL Y RESIDUOS EN SISTEMAS ELÉCTRICOS
Análisis Modal de Sistemas Eléctricos de Potencia
El concepto de estabilidad de pequeña señal corresponde a una subclase de estabilidad de ángulo del rotor debido a la presencia de pequeñas perturbaciones. Situación que obliga al operador del SEP a realizar ajustes en el despacho de la generación para abastecer la demanda.
La necesidad de monitorear la estabilidad del SEP mediante simulaciones requiere del modelo no lineal del sistema en el dominio del tiempo, caracterizada por ecuaciones dinámicas. Sin embargo, la simulación en el dominio del tiempo no suministra mucha información sobre la estabilidad, sino únicamente el status de estable o inestable.
Dada la característica de la estabilidad de pequeña señal, las ecuaciones que representan la dinámica del sistema, pueden ser linealizadas alrededor del punto de equilibrio, y con ello obtener información adicional de la estabilidad del SEP como es: nivel de estabilidad y frecuencia de los modos de oscilación. Dicha información tratada adecuadamente permite parametrizar los dispositivos de control y monitoreo de la estabilidad del sistema y de ser el caso establecer alarmas o desplazar los modos críticos de oscilación de esta manera incrementar el nivel de amortiguamiento del sistema.
A partir de la teoría de control, se determina que la dinámica de un sistema no lineal depende del nivel de transferencia y capacidad de procesamiento de la energía entre las distintas partes del sistema tanto en la operación como en la perturbación. Dado que los sistemas de potencia son sistemas no lineales de gran escala, se caracterizan por estar sujetos a la presencia de oscilaciones de baja frecuencia (, ).
Este fenómeno oscilatorio es recurrente en la operación del sistema que se distingue por ser cuasi-estacionaria, debido a las pequeñas variaciones presentes en las condiciones de operación para abastecer la carga, característica que permite linealizar la dinámica del sistema alrededor del punto de equilibrio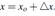 , como se muestra en la Ecuación que representa el modelo linealizado ( , ; , ).
, como se muestra en la Ecuación que representa el modelo linealizado ( , ; , ).
Donde x ϵ ℝ, representa el vector de estado del sistema, y ϵ ℝ corresponde al vector de las salidas y u ϵℝ es el vector de las variables de entrada. Además, A es la matriz de estado del sistema, B es la matriz de las señales de entrada o de controlabilidad, C es la matriz de las señales de salida o de observabilidad y D es una matriz que define la proporción de la entrada que aparece directamente en la salida.
Los valores propios de la matriz de estado A son aquellos que satisfacen la Ecuación y . Por lo tanto, para cada valor propio λ i se tiene dos vectores propios. En consecuencia, el vector propio derecho φ i es un vector columna con una longitud igual al número de estados. El vector propio izquierdo ψ i es un vector fila (, ; , ).
Donde λ i ϵ C es el i-ésimo valor propio de la matriz A, permite determinar la estabilidad del sistema. El valor propio λ i tiene la forma . La parte real representa el amortiguamiento (ζ ) y la parte imaginaria corresponde a la frecuencia de oscilación ( f ) de un modo de oscilación que se presenta en la Ecuación y (, ; , ).
Por medio del procesamiento de la matriz de señales de entrada B y la matriz de señales de salida C en conjunto con el vector propio para un modo de oscilación particular, es posible calcular el índice de controlabilidad del k-ésimo modo de oscilación relativo a la i-ésima entrada como lo establece la Ecuación . De manera semejante, se calcula el índice de observabilidad del k-ésimo modo de oscilación para la j-ésima salida se define de acuerdo con la Ecuación (, ; , ).
Por medio de las Ecuaciones y con la i-ésima señal de entrada de la matriz B y la j-ésima señal de salida de la matriz C se obtiene la controlabilidad y observabilidad del modo de oscilación. Que en conjunto forman el residuo del modo de oscilación como lo establece la Ecuación . Un caso particular, es cuando el residuo de un modo de oscilación es cero por alguno de los índices, por lo que se dice el modo de oscilación no es controlable o no es observable (, ; , ).
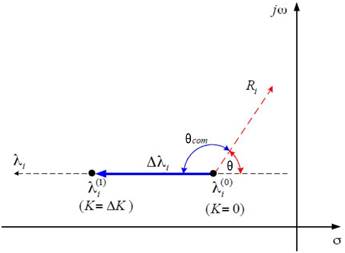
R ji ϵ C el ángulo θ del residuo del modo de oscilación da la dirección en la que se desplaza el lugar geométrico de las raíces de este. Por lo que, para incrementar la estabilidad del sistema se requiere incrementar la parte real del modo de oscilación en la dirección del complemento del ángulo θ , como se muestra en la Figura . Mediante este desplazamiento del modo de oscilación se puede utilizarlo para la sintonización de los parámetros del PSS. Por lo tanto, el PSS contribuye al desplazamiento de los modos de oscilación críticos para incrementar el nivel de amortiguamiento. Por consiguiente, el desplazamiento del valor propio se puede calcular mediante la Ecuación (, ).
Cálculo del residuo
A partir de la Ecuación , se establece que el residuo R ji indica la participación y sensibilidad del modo analizado ante las señales de entrada y salida seleccionadas para retroalimentar el dispositivo de control.
El cálculo de los residuos requiere de los valores propios de la matriz de estado A, los vectores propios y las matrices B y C. Sin embargo, como se indicó, PowerFactory no proporciona las matrices B y C. En (), se presenta una propuesta para la construcción de las matrices B y C en el Lenguaje de Programación DIgSILENT de PowerFactory. Por medio de un adecuado procesamiento de las columnas de la matriz B para el k-ésimo vector propio izquierdo y las filas de la matriz C con el j-ésimo vector propio derecho, es posible calcular el residuo del modo de oscilación de interés.
El comando análisis modal de PowerFactory permite obtener la matriz de estado A la cual se caracteriza por ser única para una configuración del sistema, a diferencia de las matrices B y C, ya que dependen de la selección de las entradas y salidas. La matriz B se la forma a partir de la variación de las variables de estado frente a un cambio en la potencia activa de la barra i seleccionada, con lo cual se determina la columna i de la matriz B, como lo establece la Ecuación .
Considerando x (0) = 0 y el paso de tiempo ∆t = 0, 0001s el error para determinar B i de la Ecuación es mínimo, este paso de tiempo es seleccionado con base en los análisis presentados en () después de comparar la respuesta de la representación no lineal completa y el modelo linealizado en un sistema. La matriz C se forma según la disponibilidad o no de las variables de los elementos de salida, se define la i-ésima fila de esta matriz con ceros excepto por un término con valor “1” asociado con la existencia del i-ésimo generador.
Esquema de sintonización del PSS considerando el residuo
En la práctica, los sistemas toman medidas de control efectivas para amortiguar las oscilaciones. Los dispositivos generalmente utilizados para esta tarea son los estabilizadores de sistema de potencia que proporciona una señal de control suplementaria a los sistemas de excitación de los generadores.
El PSS es un dispositivo que permite desplazar los modos de oscilación de interés, a través de la inyección de su señal en el regulador de voltaje. Por medio de esta señal, se busca incrementar el nivel de amortiguamiento del o los modos de oscilación seleccionados, a través de los parámetros de sintonización calculados mediante el residuo de los modos de oscilación de interés.
La Figura muestra la estructura y los parámetros del PSS modelado utilizando el lenguaje de simulación DIgSILENT (DSL) de PowerFactory. El bloque de ganancia, denotado por Kpss, permite amplificar la señal de entrada. La constante de tiempo del filtro washout (T w ) permite filtrar la frecuencia de la señal de entrada a frecuencias en el rango de los modos de oscilaciones de interés. Para el estudio esta constante de tiempo se establece en 10 segundos. Por otro lado, se utilizan filtros denominados bloques de compensación de fase de adelanto y atraso por medio de los cuales se busca desplazar el modo de oscilación seleccionado a fin de que alcance un amortiguamiento mayor en el segundo cuadrante del plano complejo en función de la magnitud del residuo. Un adecuado procesamiento de esta información hace posible obtener cada uno de los parámetros de sintonización del PSS aplicando las Ecuaciones a , como se establece en () y ().
Donde K PSS y las constantes de tiempo T k , T l del PSS se sintonizan mediante el ángulo θ del residuo R i del i-ésimo modo seleccionado, a fin de que todos los modos de oscilación del sistema alcancen el nivel de amortiguamiento deseado ζ selec para la red eléctrica. Entonces, con la sintonización de los parámetros del PSS se busca desplazar la parte real del modo λ i hacia la izquierda en el plano complejo, como se indica en la Figura 1. Cada constante de tiempo del bloque de adelanto-atraso por medio de los ángulos de los residuos de diferentes modos de oscilación permite ampliar las frecuencias sensadas por el PSS a través de más bloques de adelanto-retraso, sin embargo, de acuerdo con la práctica se observa que con dos bloques de adelanto-retraso es posible incrementar el nivel de amortiguamiento para esta clase de PSS (, ).
PROPUESTA DE CÁLCULO DE RESIDUOS
Con base en lo indicado, en la sección anterior para calcular los residuos de un modo de oscilación de interés en PowerFactory, se requiere obtener la matriz de estado A, los vectores propios izquierdo y derecho obtenidos al ejecutar el comando análisis modal (ComMod*). Adicionalmente, es necesario construir la matriz de señales de entradas B y la matriz de señales de salidas C y estructurarlas apropiadamente. Por medio de las cuales, se utilizan las Ecuaciones y para obtener el residuo y aplicarlo para el desplazamiento del modo seleccionado, por otra parte, calculando los parámetros del PSS con las Ecuaciones a permite determinar los parámetros de sintonización del PSS.
En la variable de estado del modo de oscilación seleccionado en este trabajo, se considera la velocidad del generador, gracias a la información que PowerFactory proporciona en el archivo de texto VariableToIdx − Amat.txt. Con esto, se puede utilizar la variable de estado que requiera el usuario. Todo este procesamiento de información se ha implementado en un código DPL que automatice la obtención del residuo del modo de oscilación deseado.
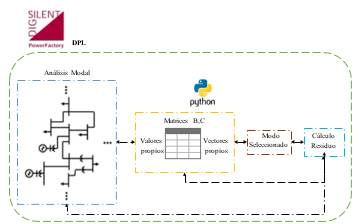
La Figura presenta la metodología que permite obtener el residuo, en la cual mediante el análisis modal, se obtiene tanto los valores propios y vectores propios del modo de oscilación seleccionado. Y con la fila o columna correspondiente de las matrices B y C procesadas respectivamente para la variable de estado monitoreada para el análisis.
Programación DPL para el residuo
Esta sección presenta las consideraciones particulares del código de programación implementado en PowerFactory mediante el cual permite calcular los residuos para una red eléctrica, mediante el comando de análisis modal en la programación DPL en conjunto con programación en lenguaje Python. Mediante la combinación de los dos lenguajes de programación es posible la importación y exportación del script para el cálculo de los residuos ante nuevas versiones del software, situación que debe ser manejada adecuadamente en las versiones de Python, debido a que por un lado PowerFactory maneja un rango limitado de estas versiones y por otro lado, existe la posibilidad de la modificación de ciertos comandos o librerías entre cada versión de Python.
Para realizar el análisis modal en PowerFactory se requiere ejecutar el objeto ComMod* en conjunto con el cálculo de las condiciones iniciales de la red eléctrica mediante el objeto ComInc* . Una vez ejecutados, es posible configurar la exportación de la matriz de estado del SEP (Amat.mtl), valores propios (Evals.mtl), vectores propios: izquierdo (IEval_Amat.mtl) y derecho (rEval_Amat.mtl) para que se almacenen en una ruta personalizada por el usuario. Cabe mencionar que estos archivos tienen una estructura establecida por el software PowerFactory de DIgSILENT.
Como los PSS son dispositivos de control ubicados en el sistema de excitación de los generadores y dado que PowerFactory permite monitorear a selección del usuario en cada barra la velocidad del rotor del generador conectado a la misma. No obstante, si el usuario considera, se podría seleccionar otra variable de estado de acuerdo a las necesidades del análisis. En este trabajo, para la programación de la matriz B cuya columna j ésima es necesario considerar la variación de la potencia en las barras seleccionadas por el usuario, mediante el comando selección general SetSelect*, en las cuales esté activa la variable de estado velocidad del generador. De acuerdo con la Ecuación , se considera la conexión/desconexión mediante el objeto EvtSwitch* en un ∆t = 0, 0001s a través de un interruptor, (ElmTerm*) una carga móvil de 100 MW.
En el caso de la construcción de la fila i-ésima de la matriz C, su tamaño depende del número de barras seleccionadas por el usuario mediante el comando selección general (SetSelect*), donde el valor “1” indica la presencia del PSS del generador conectado en la misma, caso contrario se colocará “0”.
Con esta información, es posible determinar el residuo a través de las Ecuaciones a , donde el k-ésimo vector propio izquierdo y derecho de cada valor propio del modo de oscilación de interés son obtenidos de la lectura de los archivos “Evals.mtl”, “IEval_Amat.mtl” y “rEval_Amat.mtl”, respectivamente.
SISTEMAS DE ESTUDIO Y ANÁLISIS DE RESULTADOS
La propuesta planteada para el cálculo del residuo se aplica a dos sistemas de prueba que se caracterizan de acuerdo con () por ser sistemas multimáquina y presentar uno o varios modos de oscilación poco amortiguados cuando no actúan los PSSs. En la Tabla 1, se presenta los modos de oscilación para los sistemas de prueba seleccionados. Los resultados y los datos de los sistemas estudiados, el lector lo puede obtener del enlace https://github.com/jaoscullo/My-PowerFactory.
En el contexto del análisis modal, los modos de oscilación se clasifican en locales, intraplanta e interárea. Los modos locales se presentan cuando algunos generadores de un área delimitada oscilan respecto al resto de generadores del sistema, el rango de frecuencia típico es del orden de 1 a 2 Hz, se caracterizan en que estas oscilaciones son observables por mediciones locales. Los modos de oscilaciones interárea se presentan en las oscilaciones de un grupo de máquinas sincrónicas de una parte del sistema respecto a un grupo de máquinas de otra parte del sistema interconectadas a través de vínculos que tienden a congestionarse, el rango típico de frecuencia es del orden de 0,1 a 1 Hz.
Los modos de oscilación intraplanta se presentan para las oscilaciones entre generadores de una misma planta siendo la frecuencia de los mismos del orden de 2 a 3 Hz.
A continuación, se presenta la distribución de los distintos dispositivos y elementos de cada uno de los sistemas de prueba:
Sistema equivalente sudeste Brasil
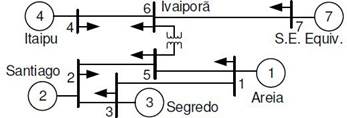
En la Figura , se presenta el diagrama equivalente de 7 barras del sistema eléctrico sureste brasileño, el cual está conformado por cinco generadores. Este sistema se caracteriza por presentar modos de oscilación interárea, los cuales tienen problemas de controlabilidad y observabilidad. Por lo indicado, resulta interesante considerar el uso del residuo para establecer el desplazamiento de los modos de oscilación a la zona estable.
Sistema New York-New England
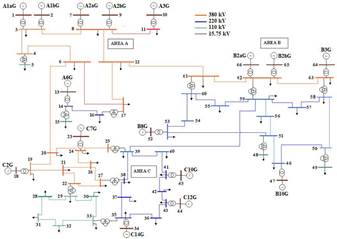
El sistema de prueba New York-New England de la Figura es uno de los sistemas más utilizado en la literatura especializada sobre el amortiguamiento de los modos de oscilación, se conforma por tres áreas fuertemente malladas, 66 barras, 16 generadores, 28 transformadores, 52 líneas de transmisión. Los modos de oscilación local e interárea caracterizan la estabilidad del sistema y resulta un reto interesante para la sintonización de los PSSs, considerando la determinación de los residuos de los modos de oscilación de interés.
Caso: Sistema Equivalente Sudeste Brasil
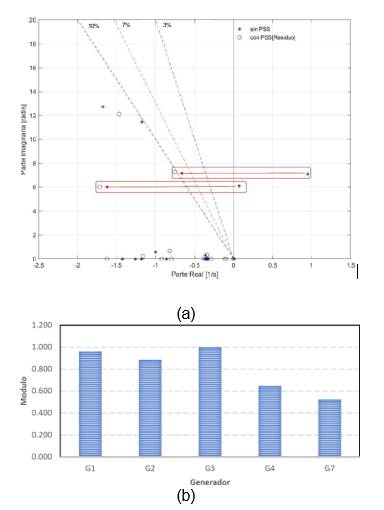
Utilizando las herramientas desarrolladas para determinar el residuo y dinámica de los modos de oscilación críticos, en la Figura (a), se presenta la dinámica de los modos de oscilación del sistema, tanto para el escenario sin PSS y escenario con los PSS sintonizados mediante el uso del residuo de los modos de oscilación críticos. Los modos de oscilación inestables y de baja frecuencia de acuerdo con () son poco controlables al utilizar factores de participación para la sintonización de PSS. Sin embargo, mediante el uso de los residuos se logra alcanzar un nivel robusto de estabilidad, los modos alcanzan un amortiguamiento del 10 %. En la Figura (b), se muestra el módulo de los residuos de uno de los dos modos de oscilación crítico donde los generadores G 1 a G 3 tienen la mayor participación que corresponde a los modos de oscilación resaltados que presenta un nivel de amoritguamiento de -0,99, es decir es inestable por lo que se encuentra en el primer cuadrante del plano complejo, con una frecuencia de 1,13 Hz como puede observar en la Figura (a).
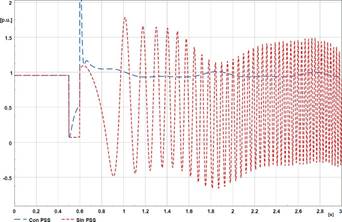
Como se presenta en la Figura , la simulación en el dominio del tiempo de la variable potencia activa del generador G 4 para el caso de que el sistema se somete a un cortocircuito en la línea 4-6 a los 0,5 s y despejada a los 0,6 s en el escenario con PSS alcanza rápidamente una operación estable al segundo de la simulación. Para el caso del escenario sin PSS, el sistema es inestable ante esta perturbación, como se observó en la Figura (a) el sistema presenta modos de oscilación inestables.
Caso: Sistema New York-New England
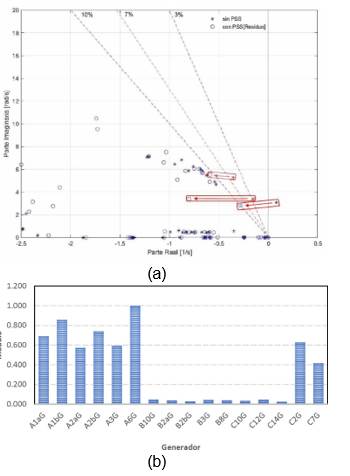
Para investigar la aplicabilidad de las herramientas computacionales desarrolladas en un sistema eléctrico más grande, el cual presenta una mayor cantidad de modos de oscilación, y de acuerdo con la literatura especializada es un sistema que demanda una alta coordinación en la sintonización de los PSS de los generadores que los tengan disponibles, para el caso del estudio se considera que todos generadores cuentan con PSS. En la Figura (a), es posible observar la distribución de los modos de oscilación para el escenario sin PSS, que muestra tres modos de oscilación interárea con frecuencia promedio de 0,62 HZ y niveles de amortiguamiento bajos e incluso inestables.
En la Figura (b), se presenta el módulo de los residuos correspondientes al modo de oscilación inestable que presenta un nivel de amortiguamiento de -0,46 %. Situación que requiere de un nivel de controlabilidad y observabilidad alto como lo indica (). No obstante, con el uso de los residuos para la sintonización de los PSS se alcanza un nivel de amortiguamiento de todos los modos de oscilación sobre el 10.
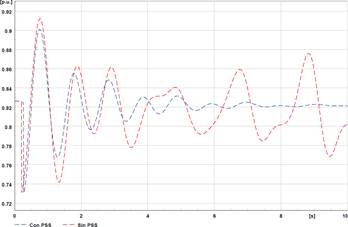
En el escenario sin PSS, se considera una falla trifásica en la línea B-C a los 0,5 s y se resuelve a los 0,6 s. Además, se observa que el sistema, al no contar con los PSS, presenta oscilaciones que conducen a la inestabilidad del sistema. Con el desplazamiento de los modos de oscilación críticos por medio del residuo, como se muestra en la Figura (a), la respuesta en el dominio del tiempo de la potencia del generador C 7G, que tiene activado su PSS, muestra que las oscilaciones se amortiguan y presenta una operación cuasi-estacionaria a partir de los 6 segundos, como se ilustra en la Figura .
CONCLUSIONES
En este estudio, se demostró que mediante un procesamiento adecuado de variables y la construcción de matrices, es posible programar una herramienta para calcular los residuos de los modos de oscilación de interés en una condición operativa de un SEP utilizando un software de ingeniería. Adicionalmente, se evidenció que el residuo de un sistema eléctrico indica el nivel de controlabilidad y observabilidad de los modos de oscilación críticos y puede ser utilizado para determinar los parámetros de sintonización de elementos de control de oscilaciones, como los PSS.
Al identificar el residuo más alto del modo de oscilación analizado, es posible ubicar, activar y sintonizar los PSS de los generadores asociados a dicho residuo. Esta situación facilita alcanzar un nivel de amortiguamiento seleccionado por el usuario, basado en la literatura especializada que sugiere un 10 % para sistemas pequeños y un 7 % para sistemas de gran escala. Por medio de los residuos, se logra desplazar los modos de oscilación del sistema.
Este trabajo demostró que con un procesamiento adecuado de variables de interés, es posible automatizar la construcción de las matrices B y C. Estas matrices pueden ser utilizadas para determinar variables que contribuyan a mejorar el nivel de estabilidad de un sistema eléctrico. Asimismo, pueden ser utilizadas para resolver diferentes problemas de ingeniería eléctrica dentro del entorno de software de ingeniería como PowerFactory, manteniendo una interfaz amigable con el usuario.