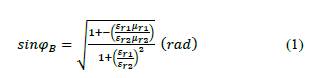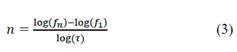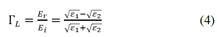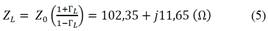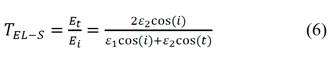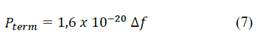1. INTRODUCTION

In Colombia, the Military Forces have identified that more than 90% of antipersonnel mines are made using handmade materials, plastic, and homemade explosives (Gutiérrez, 2014). Clearance techniques such as manual inspection of the terrain, mechanical (mine sweeping machines: tiller, flail, or others), and the deployment of mine detection canines (CDM) are ineffective for this type of mine. For this reason, it is necessary to continue researching new methods and technologies for the detection of this type of mines and explosive devices. This article reports the performance results of the fractal antenna as a transducer for a GPR, as an alternative for the detection of plastic mines. The physical principle of GPR is extracting information from the plastic mine buried in the ground by comparing two signals: the one emitted and the one reflected by the buried object, with sufficient signal-to-noise ratios to be processed.

A fractal can be defined as a semi-geometric object characterized by a structure that repeats itself at different scales (^{Castro Fonseca, 2015}). The science that studies these complex and irregular elements through geometric and mathematical algorithms is Fractal Geometry (^{Herrera Holguín & Inclán Luna, 2004}). This geometry has had an impact on different areas of science including medicine, physics, engineering, and telecommunications (Montoya, 2012), as it is the case with the design and simulation of antennas. Some fractal models used in antennas are Koch curves, Sierpinski triangles, and fractal trees, which take advantage of their natural multi-band capacity to minimize the antenna area (Montoya, 2012). In his research, ^{Figueroa Torres (2016}) proposes a fractal antenna based on the Sierpinski triangle to obtain a super-wide band antenna, which operates in the frequency range from 1,7 GHz to 26 GHz. Castro Fonseca (2015) presents the design of antennas based on the Koch curve, operating in the range of 470 MHz to 700 MHz, to be used in digital television service. In his thesis, Oltra (2009) designs and constructs a multiband fractal antenna based on the Hilbert curve to be used in cellular mobile telephony services.

Some antenna applications in antipersonnel mine detection systems in the international context use GPR systems operating in the microwave range. In the investigation carried out by ^{Giannakis, Giannopoulos & Warren (2016}), two tie-type antennas were used as transducers of a GPR system for 1,2 GHz and 1,5 GHz, respectively. In (^{Zainud-Deen, et al., 2009}) the detection capacity of two parallel Microstrip antennas with corrugated earth as a propagation medium is studied. ^{Lopera et al. (2007}) propose filtering the reflections between the antenna and the ground in a radar system, as a strategy to improve the detection of antipersonnel mines.

In the national context, the project carried out by Mendoza & Serrano (2014) was identified, they developed an SDR (software-defined radio) platform and a prototype of a GPR system, with two VERT 900 dipole antennas, and two Vivaldi antipodal antennas (directive antennas), for the detection of antipersonnel mines. ^{Baer et al. (2018}) reported laboratory measurements for a GPR system consisting of a dual-polarized Vivaldi antenna, a maximum gain of 9 dBi, and a frequency range of 0,8 to 5 GHz.

The review of the state of the art made it possible to show a variety of antennas and Anti-Personnel Mines detection methods, this reflects the importance of this type of study for society. However, the use of fractal antennas for this purpose was not identified, for this reason, this investigation of the fractal antenna for the detection of plastic mines was carried out, which represents a contribution to the humanitarian demining processes from electronic engineering. This article is structured in four sections: the methodology, which describes the process used in the bibliographic search, proposal of the solution, relevant calculations and simulations carried out. In the results section, the results obtained from the simulations for the transmission and reception circuits proposed in the methodology are presented; in the discussion of the results section, the results obtained and their impact on the desired objective are analyzed. And finally, the conclusions of the work developed are presented, highlighting the relationship of the results with the proposed objectives.

2. METHODOLOGY

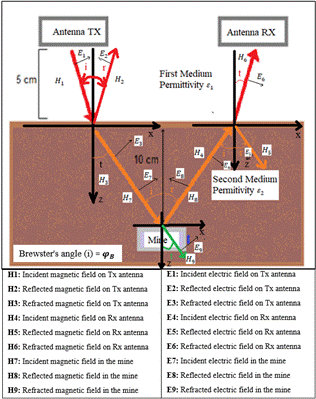
The methodology was structured in four phases: 1) review of the reference framework, 2) design and simulation of the log-periodic fractal antenna, 3) characterization and modeling of the transmission media, and the antipersonnel mine, and 4) calculation of the energy balance of the electromagnetic wave radiated from the antenna in the direction of the ground and towards the mine buried at a depth of 10 cm, and reflected towards the receiving antenna, as shown in Figure 1.

The first phase revolved around identifying the theoretical background related to the properties of buried plastic mines, and the detection system using GPR (^{Giannakis et al., 2015}). GPR was chosen because it is sensitive to non-metallic materials, such as plastic- (Giannakis, Giannopoulos & Warren, 2016), propagation of electromagnetic waves in two lossy media, Brewster's pseudo-angle of incidence, and antennas fractals, which allowed to identify the requirements for the design and simulation of the fractal antenna; among other requirements. The following are mentioned: broadband, preferably in the microwave band between 1 GHz and 3 GHz because it is the operating frequency range of the GPR, return loss less than -10 dB, a higher gain or equal to 6 dBi, input impedance of 50 Ohm and antenna tilt with the pseudo-Brewster angle to reduce power losses in the free space-ground transition (^{Sadiku, 1998}).

Figure 1 Electromagnetic wave propagation back and forth 

Brewster's pseudo-angle or angle of least reflection is applied to minimize the power of the signal reflected by the transition between non-perfect, lossy, and frequency-dispersive dielectric media such as free space and the ground; allowing as much electromagnetic energy as possible to be transferred from the log-periodic fractal antenna to the ground. The main radiated lobe illuminates the ground with an inclination equal to that of the pseudo-Brewster angle so that the magnitude of the polarized EV wave is transmitted through the boundary and a reflection coefficient tending to zero is obtained (^{Ohman, 1977}); this incidence angle is found with Equation 1.

Where ε _r1 , and μ _r1 are respectively the electrical permittivity and magnetic permeability for medium 1, and ε _r2, μ _r2 are the electrical permittivity and magnetic permeability for medium 2.

The next step was the development of phase 2: design and simulation of the fractal antenna. The chosen design was based on ^{Amini, Oraizi & Zadeh (2015}), with a slight variation: a log-periodic antenna made up of rhombic patches. This type of antenna has a reduced form factor, wide bandwidth, stable radiation pattern, and multi-resonance which are desirable for the particular case of detecting antipersonnel mines made of plastic containers. Under these characteristics, the input impedance is real at multiple resonance frequencies and couples better with the transmission line, achieving maximum energy transfer to the antenna, greater radiated power, and reflected signals with a better signal-to-noise ratio.

The antenna was designed in CST Microwave Studio 2018® with the following characteristics: average scale factor of τ=1,1065, six diamonds for six resonance frequencies, PTFE woven glass substrate dimensions of 28,0 cm x 20,4 cm, a thickness of 1,52 mm, and relative electrical permittivity of ε _r = 2,50.

The scale factor τ was obtained with Equation 2 and the number of iterations with Equation 3 (^{Sadiku, 1998}).

Where τ is the scale factor, f _n is the resonance frequency of the nth iteration, f ₁ is the initial frequency, and n is the number of iterations of the fractal antenna.

The resonance frequencies for each of the iterations are shown in Table 1.

Table 1.  Log-periodic fractal antenna resonance frequencies 

In phase 3, the physical phenomenon of the propagation of the electromagnetic wave -outward and return- was modeled through two lossy media: free space and ground; for which it was necessary to characterize these media for specific conditions of the lower Cauca sub-region of the department of Antioquia, Colombia (^{Díaz Diez, 2020}). In this process, the procedures suggested by ^{Sadiku (1998}) and ^{Hipp (1974}) were taken as a reference. The explosive device was also characterized by the physical properties and the procedure reported in ^{Pantoja et al., (2014}), to model it as a load impedance.

The electrical properties of free space and soil, which define the speed of propagation of GPR waves and their amplitudes, as well as the dimensions of the bounded area of the soil sample, specified in Table 2, of the sub-region outlined above, allowed through the application of electromagnetic theory and simple calculations, obtain the primary parameters R, L, C, and G, per length unit, and secondary parameters α, β, Z _o per length unit, from Table 3, for both transmission media.

2 Physical and electrical properties of free space and soil sample for the lower Cauca subregion of the department of Antioquia 

Table 3 Primary clearance, floor parameters and secondary parameters of free space and soil 

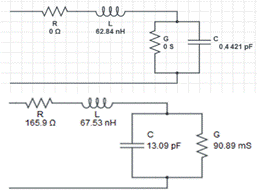
Once the two transmission media were characterized, they were modeled using their respective equivalent circuits in distributed parameters, as shown in Figure 2.

To characterize and model the plastic mine, we started from the concept of the reflection coefficient in the charge Г L between two non-conductive and non-magnetic materials; this is defined as the ratio between the electric field intensity vector reflected in the load (plastic container mine) over the incident electric field intensity vector coming from the source (fractal antenna and passing through two transmission media).

Figure 2 Equivalent circuit for free space (top) and Equivalent circuit for ground (bottom) 

The value of this parameter was obtained with Equation 4, taking as a reference the relative permittivity of the soil ɛ ₁ , which was ɛ ₁ = 7,9, and the relative permittivity of the plastic container mine ɛ ₂ with Polyethylene Terephthalate material (also known by its acronym PET), which was of ɛ ₂ = 3,65 respectively.

The substitution of the value of the reflection coefficient of 0,192, in Equation 5, allowed us to find the value of the load impedance Z _L that models the plastic mine. In this equation, the value of Z _O corresponds to the characteristic impedance of the transmission line, where a value of 50 Ohms is used, a value that is considered optimal for reducing attenuation (^{Sadiku, 1998}).

For the development of phase 4, the equivalent circuits were interconnected in distributed parameters, which model the free space and ground transmission media, with the circuit model of the mine represented in a Z _L ; the signal source that feeds the circuit is 30 V (this level corresponds to 20,6 W rms for a radiation impedance of 43,74-j3,51 Ω at a frequency of 1,35 GHz), which is equivalent to the radiated power by the log-periodic fractal antenna with a pseudo-Brewster angle of incidence of 70,47°. Figure 3 shows the equivalent circuit for the forward simulation.

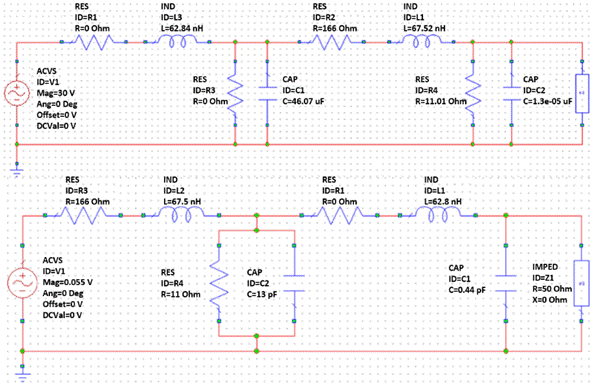
Figure 3 Equivalent circuit of the system for the forward signal (top) and system equivalent circuit for the return signal (bottom) 

Figure 3 shows the equivalent circuit for the return signal (A-Scan). In this case, the source represents the signal reflected by the plastic lead, the two equivalent circuits connected in cascade represent the two-transmission media: the ground and free space respectively, and the load impedance of 50 Ω represents the input impedance of the spectrum analyzer antenna, which acts as a signal receiver. This is located next to the fractal antenna, but electromagnetically isolated.

The simulation of the propagation of the signal from the fractal antenna (source) to the buried plastic mine (charge), and its reflection towards the receiving antenna, was done in the Cadence AWR® software for six resonance frequencies of the log-periodic fractal antenna.

3. RESULTS

The simulation of the fractal antenna with the CST Microwave Studio 2018® software, for the six resonance frequencies, was done to identify the dispersion parameter S_11, VSWR, and verify uniformity in the radiation pattern of the main lobe. Figure 4 shows that the best values of the dispersion parameter S_11 of -9,08 dB and -32,29 dB correspond to the frequencies of 1,35 GHz and 2,95 GHz, respectively.

Figure 4 shows that for the frequencies of 1,35 GHz and 2,95 GHz the lowest values of VSWR are presented, which is desirable.

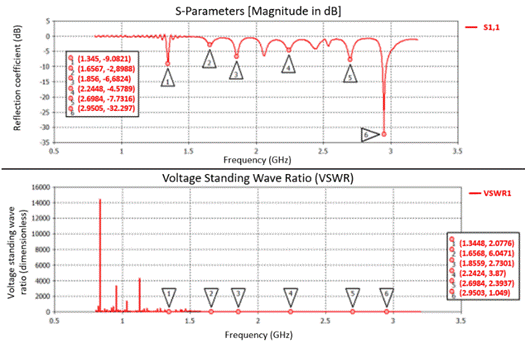
Figure 4 Log-periodic fractal antenna parameter S₁₁ (top) and VSWR of log-periodic fractal antenna signal 

Likewise, it was observed, for the frequencies of 1,35 GHz and 2,95 GHz, greater directive gain, uniformity in the radiation pattern of the main lobe (Figure 5), and beam widths, which allow inferring a bandwidth that goes from 1,19 GHz to 1,36 GHz, for the 1,35 GHz resonant frequency, and from 2,8 GHz to 2,95 GHz for the 2,95 GHz resonant frequency.

Figure 5 Largest directives gain and beam width for two of the six resonance frequencies of the log-periodic fractal antenna 

From the results of the simulation of the log-periodic fractal antenna, it can be inferred that 1,35 GHz and 2,95 GHz are the resonance frequencies with the best performance in the simulation of the parameters indicated above. Taking the simulation results as a reference, the log-periodic fractal antenna was built with direct coupling feeding with SMA, shown in the annexes. The results obtained in the simulations for six resonance frequencies of the log-periodic fractal antenna, for the circuits presented in Figure 3, are shown in Table 4. They are expressed in terms of power in the plastic load and power at the input of the receiving antenna for the return signal.

Table 4 Results obtained in the simulation 

The resonance frequency of 1,35 GHz shows 224,5 pW, which is the highest power transferred in the free space-ground, ground-mine transitions (for the forward signal) and reflected by the mine towards the receiving antenna.

Figures 6a and 6b show the Matlab simulation of the standing wave (incident and reflected) at a resonance frequency of 1,35 GHz, which is transmitted from the fractal antenna (with the pseudo-Brewster angle of 70,47°) and propagates through free space in the direction of the buried plastic mine at 10 cm (forward). This signal passes through the free space-ground transition (Figure 6a), propagates through the ground, and is reflected in the mine (Figure 6b).

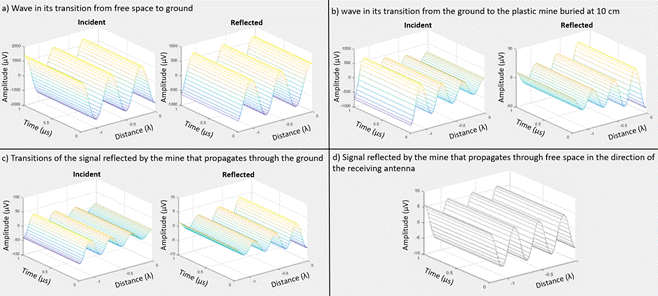
Figure 6 (a) Incident and reflected wave in its transition from free space to ground, (b) incident and reflected wave in its transition from the ground to the plastic mine buried at 10 cm, (c) transitions of the signal reflected by the mine that propagates through the ground and (d) signal reflected by the mine that propagates through free space in the direction of the receiving antenna 

The electric and magnetic fields of the incident reflected, and transmitted waves are perpendicular to their propagation directions, due to an inherent property of plane waves; no attenuation is evident in the incident and reflected waves in free space and their magnitudes change due to the reflection coefficient in the transition of the two media. Figure 6b shows the wave transmitted from free space to the ground, which is proportional to the transmission coefficient of Equation 6 (^{Sadiku, 1998}).

Where ɛ ₁ is the relative permittivity of free space, ɛ ₂ is the relative permittivity of the ground; (i) is the angle of incidence of the simulated GPR wave, which is equivalent to Brewster's pseudo-angle of incidence of 70,47°, (t) is the transmission angle, E_t is the refracted electric field, E_i is the incident electric field, and T_EL-S is the transmission coefficient. Figure 6b shows considerable attenuations of 1,89 Np/10 cm in the propagation through the ground and reflected power of µW in the plastic mine.

Figures 6c and 6d show the Matlab simulation of the electromagnetic wave reflected from the discontinuity (plastic mine buried at 10 cm) to the receiving antenna; this signal propagates through the ground (incident wave of Figure 6c), undergoes a transition in the change of medium to free space (incident wave of Figure 6d) and propagates without attenuation through this medium until it reaches the receiving antenna.

The value of the power of the signal received at the receiving antenna must be greater, at least 10 times, than the value of the thermal power of the GPR so that it can detect the discontinuity or buried object. The thermal power of the GPR is calculated with Equation 7.

Where ∆f is the resonance frequency of the transmitting antenna.

If the power received in the GPR antenna of 224,5 pW is related to its theoretical thermal power of 21,6 pW, for the resonant frequency of 1,35 GHz, the signal-to-noise ratio (hereinafter SNR) is obtained 10,4 times (10,17 dB).

4. DISCUSSION OF THE RESULTS

Current GPR systems have the drawback of a high rate of false alarms due to the low SNR present in the operation of the System. For this reason, it is desirable that: 1) the power radiated by the log-periodic fractal antenna be greater than 20,6 W rms so that the returning electromagnetic wave guarantees an SNR greater than 10,17 dB; 2) the Medium of propagation: free space and ground, are homogeneous and sufficiently resistive to avoid total attenuation of the signal before completing its path; 3) the size of the log-periodic fractal antenna is comparable to the wavelength of the emitted signal; 4) the electromagnetic properties of the transmission media: free space and ground are homogeneous along their respective lengths, and in their outward and return transitions favor the transmission of the electromagnetic wave; 5) the electromagnetic properties of the soil and the buried plastic mine are testable so that a reflection coefficient tending to one is produced so that the GPR is capable of detecting the buried plastic mine.

A promising alternative to address the problem of false alarms in the GPR -under real conditions of floors, laminates, non-homogeneous and variants in the frequency domain, due to the presence of water and other materials that change their electrical characteristics-, is the exploitation of the physical principle of maximum power transfer to the ground, when it is radiated at a certain angle, known as pseudo-Brewster, which would allow the increase of the SNR in the GPR.

This investigation confirmed the dependence of the pseudo-Brewster angle and the soil dielectric constant. The calculated value for the pseudo-Brewster angle is 70.47 degrees. This angle represents the angle of least reflection in which the field component parallel to the plane of incidence is minimized, resulting in less dispersion due to overlapping with the returning electromagnetic wave. Achieving an SNR in the GPR greater than 10 times is guaranteed. Unfortunately for this type of applications and as corroborated by ^{Merve & Gupta (2000}), the dielectric constant of the soil varies throughout the area of the buried plastic mine, preventing the determination of a unique pseudo-Brewster angle for this type of application.

The results obtained for both simulations show very small amplitude values compared to the signal originally transmitted by the log-periodic fractal antenna; this is mainly due to the heterogeneity of the physical-chemical and biological properties of the soil, and its attenuation of 1.89 Np/10 cm, which affects both the wave that impacts the buried plastic mine and the wave that is reflected from it.

4. CONCLUSIONS

The receiver SNR of 10,4 times meets the criteria of being at least 10 times higher; consequently, the log-periodic fractal antenna can be used by the GPR at the resonance frequency of 1,35 GHz, for the detection of the plastic mine.

The biggest challenge in achieving the detection of a plastic mine lies in the inhomogeneous electrical properties of the ground as it generates different reflection and refraction indices of the signal when passing from free space to the ground. In addition, the wave propagation constant shows non-linear behavior with frequency when propagating through the ground. This conclusion is based on the electrical properties of the soil reported in Table 2 and coincides with the experimental findings reported by ^{Díaz Diez (2020}).

The self-similarity principle of the log-periodic fractal antenna facilitates the multiband characteristic that gives the possibility of selecting the resonance frequency in which the best results are obtained. This characteristic of the fractal antenna increases the chances of achieving a stop with better resolutions for the GPR.

Adjusting the angle of incidence of the main lobe of the transmitting antenna to the pseudo-Brewster angle of 70.47° at the transition between two dielectric media, with losses and frequency dispersive, such as air and soil, allows the transfer of the greater amount of electromagnetic energy to the second medium, this is evident in Figure 6a to 6d.