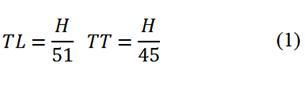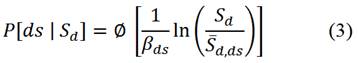1. INTRODUCCIÓN
En el proyecto de Comunicación y Formación en la Evaluación de Riesgos por Terremotos, TREQ por sus siglas en inglés, de la Fundación Global Earthquake Model (GEM), existe la necesidad de realizar evaluaciones detalladas de amenaza y riesgo de tres ciudades latinoamericanas, como son Quito (Ecuador), Cali (Colombia) y Santiago de los Caballeros (República Dominicana), con el fin de que estas evaluaciones provoquen un impacto directo en las autoridades con respecto a la comunicación e implementación de medidas de reducción del riesgo de desastres, mediante la toma de decisiones y el desarrollo de políticas públicas de reducción del riesgo.
A pesar del progreso en esta materia con la evaluación de la amenaza y el riesgo sísmico en América del Sur con el proyecto SARA y en América Central y el Caribe con el proyecto CCA, es necesario continuar con la investigación que genere modelos de acceso libre en amenaza, exposición y vulnerabilidad, mismos que permitan la evaluación armonizada y transparente del riesgo en Latinoamérica, de tal forma que se considere pérdidas humanas y económicas a causa de los terremotos.
Varias investigaciones han aportado al modelo SARA, entre ellas, la investigación de Chicaiza (2017) donde se realizó el modelo de exposición y mapa de vulnerabilidad del Distrito Metropolitano de Quito (DMQ). En esta, se levantó la información geométrica estructural de una muestra representativa de las edificaciones en la ciudad, identificando las tipologías estructurales recurrentes de la muestra.
En la investigación de Celi & Pantoja (2017), se realizaron aportes al proyecto SARA con el análisis de fragilidad con base en las curvas de capacidad calculadas y las curvas de peligrosidad sísmica del o (DMQ), este análisis fue realizado para cuatro tipologías existentes en una muestra representativa de las edificaciones. Una de estas fue la tipología 4, que determinada bajo la taxonomía del GEM, se la conoce como (CR+CIP / LFLSINF + DUC: 4, 6) (Brzev et al., 2013).
La tipología 4 analizada en Celi & Pantoja (2017) y en Celi et al. (2018), describe estructuras con losas planas, conformadas por pórticos de hormigón hecho en sitio y rellenos con mampostería. En los resultados de fragilidad obtenidos, no fue considerada la influencia de la torsión en planta en la respuesta general de la edificación, esto puede provocar falsamente un criterio de aceptación basado en las deformaciones que se presentan en un análisis estático no lineal (Flores et al., 2018).
El objetivo de esta investigación fue realizar el análisis de fragilidad de la tipología 4 considerando los efectos de torsión en planta con base en métodos estáticos directos. De esta forma, se plantea contestar a la hipótesis plantada sobre si la consideración de efectos de torsión en planta, presenta mayores índices de daño en los umbrales moderado, extensivo y completo en comparación a una estructura con efectos de torsión bajos.
El análisis utilizado para calcular las curvas de capacidad de los múltiples modelos matemáticos, está basado en métodos estáticos directos, donde se busca obtener una curva de capacidad luego de aplicar un patrón de fuerzas incremental a cada nodo de unión viga-columna. Este patrón está relacionado a cuatro formas de distribución de la fuerza con el fin de capturar los efectos de torsión que se buscan representar en la capacidad global.
La primera y segunda forma de fuerza incremental obedecen a las fuerzas que se determinan de manera directamente proporcional a las masas asignadas a cada nodo en los sentidos ortogonales de análisis. La tercera y cuarta forma de fuerza obedecen al modo fundamental y al segundo modo de vibración de la estructura, respectivamente. De esta forma, se reduce la incertidumbre existente al momento de caracterizar una estructura, ya que la respuesta sísmica puede estar dada por una de las posibles distribuciones de fuerza planteada en la edificación.
Este método asegura que los efectos torsionales puedan ser representados de forma matemática con mayor aproximación que con un método estático no lineal convencional, donde la forma de fuerza es aplicada a los diferentes niveles de la edificación y por este motivo, la respuesta del piso estará dada por la consideración del diafragma horizontal, perdiendo así información sobre la respuesta en términos de torsión en planta.
Se reconoce que muchas de las variables involucradas son altamente aleatorias, como las características estructurales y la respuesta del sistema, especialmente cuando el comportamiento de este último es no lineal (Vargas et al., 2013). Por lo que en la evaluación de la vulnerabilidad fue necesario considerar la aleatoriedad de las variables que describen el problema mediante el uso de técnicas avanzadas basadas en el proceso de simulación de Monte Carlo y los resultados de los análisis previamente indicados.
El aporte de la Entidad Colaborada de Proyectos del Colegio de Arquitectos del Ecuador CAE-P, a través de su Director General, permitió obtener información estructural y arquitectónica sobre diez proyectos que ingresaron a revisión y que forman parte de la tipología en análisis, con el fin de definir los márgenes de variación de las variables. Estos diez proyectos fueron la base para las permutaciones que se generaron mediante variaciones a las longitudes de vanos y alturas de piso, variaciones de las propiedades mecánicas de los materiales como hormigón, acero y mamposterías. También, se realizaron variaciones de la ubicación en planta y elevación de la mampostería dentro de cada modelo, así se obtuvo una base de datos densa que permitió obtener curvas de capacidad para caracterizar a la tipología 4. Este proceso fue iterativo hasta encontrar estabilidad en la variabilidad de las curvas de capacidad.
La amenaza sísmica fue determinada mediante la obtención de los espectros con base en las aceleraciones máximas esperadas en el estrato competente PGA (Peak Ground Acceleration), por sus siglas en inglés, para los periodos de retorno desde 25 a 475 años en intervalos de 10 años con variaciones de suelo tipo C y D.
Se determinó gráficamente el punto de intersección del espectro de capacidad de la estructura con el espectro de demanda. En el caso de existir este punto teórico, este tuvo su aporte para el análisis de fragilidad de la tipología estudiada mediante la metodología Hazus (Kircher et al., 2006).
Con el método indicado y aplicado en las decenas de permutaciones generadas, se pudo determinar de manera objetiva los umbrales de daño que permitieron generar las curvas y matrices de fragilidad a partir del cálculo del daño asociado al comportamiento sísmico, aplicando procedimientos probabilistas a partir de resultados de análisis deterministas (Vielma et al., 2007).
Este trabajo es una contribución al análisis de fragilidad con base en métodos estáticos directos de las edificaciones pertenecientes a la tipología 4 y aporta al análisis del riesgo sísmico en un área urbana situada en una zona de alta sismicidad enmarcado en el proyecto de la Fundación GEM.
2. ALCANCE
A partir de la información compartida por el CAE-P, se realizaron doscientos cincuenta y ocho (258) modelos matemáticos, que se dividieron en tres (3) grupos de ochenta y seis (86) modelos para estructuras de cuatro (4), cinco (5) y seis (6) pisos, respectivamente. De esta cantidad, se trabajó solamente con los modelos que permitieron encontrar una tendencia aceptable en la dispersión de los resultados.
3. MODELOS DE MATERIALES
Se presentan los resultados de la investigación realizada en el estado del arte actual para la caracterización de las propiedades mecánicas de los materiales, presentando los parámetros a utilizar y el modelo adoptado para el hormigón, acero y mampostería. No fue la intención realizar una revisión cronológica de los modelos publicados y validados, sino utilizar los resultados concluyentes de las investigaciones realizadas y aplicables al medio.
Estas propiedades de elementos serán utilizadas en la modelación que se la realizó en el programa SeismoStruct versión estudiantil (Seismosoft, 2020), mediante la consideración de que la plasticidad del miembro se distribuye a lo largo de cada una de las secciones de integración empleadas y el nivel de esfuerzo y daño es determinado por la discretización de estas secciones.
Hormigón
El modelo seleccionado para el hormigón fue el no lineal de Mander, con la denominación “con_ma” en el software, mismo que trata de un modelo de confinamiento constante no lineal uniaxial que sigue la relación de constitutiva de Mander et al. (1988) y las definiciones cíclicas propuestas por Enrique Martínez-Rueda & Elnashai (1997).
La ventaja del uso de la curva constitutiva para hormigón no confinado propuesta por Mander et al. (1988), basada en el modelo de Popovics (1973), es la facilidad de representar la gráfica del hormigón confinado mediante el uso del coeficiente k. Este asume una presión de confinamiento constante a lo largo de todo el rango tensión-deformación que puede alcanzar en la zona del núcleo confinado por la presencia del refuerzo trasversal.
Acero
El modelo seleccionado para el acero fue el no lineal de Dodd y Restrepo, con la denominación “stl_dr” en el software, ya que este mostró las mejores aproximaciones en los ensayos realizados por Pachano (2018) y Albuja & Pantoja (2017). Este modelo de acero uniaxial formulado por Dodd & Restrepo-Posada (1995) considera la reducción del módulo de descarga con la deformación unitaria plástica.
Mamposterías
El modelo adoptado para las mamposterías de relleno se basa en la investigación realizada por Pachano (2018) y Albuja & Pantoja (2017) donde se utilizan los resultados obtenidos en las calibraciones de modelos mediante el software SeismoStruct v2020 (Seismosoft, 2020) y el empleo del modelo de puntales de Crisafulli (1997).
Estas simplificaciones son válidas desde el punto de vista global de toda la estructura, ya que el puntal que se utilizó no tiene la capacidad de reproducir los efectos que tiene la zona de contacto panel-marco. Aun así, este modelo cumple con el alcance del presente trabajo de investigación, debido a que no interesa verificar la especificad de los modos de falla locales, sino la capacidad de la estructura a nivel global, por lo que, el modelo fue adecuado.
El modelo de puntales de Crisafulli (1997) se encuentra implementado en el programa SeismoStruct (Seismosoft, 2020). Este permitió obtener resultados con buenas aproximaciones al material y comportamiento de mamposterías locales. Este modelo no fue capaz de representar la interacción local entre el pórtico y la mampostería, puesto que la losa se deforma sin ningún tipo de restricción vertical en el centro del vano.
Cada una de las secciones de integración de los elementos estructurales utilizados está compuesta por elementos de tal forma que cada uno de estos responda de manera independiente según el nivel de esfuerzo y daño acumulado que tengan (Pachano, 2018).
La cantidad de secciones de integración y las fibras internas de cada elemento son utilizados con base en la experimentación en el Centro de Investigación de la Vivienda de la Escuela Politécnica Nacional, de los trabajos de investigación de Pachano (2018) y Albuja & Pantoja (2017), estos modelos fueron calibrados según los resultados obtenidos.
4. DESCRIPCIÓN DE LA TIPOLOGÍA
La tipología 4 comprende edificaciones de cuatro a seis pisos con un sistema resistente a carga lateral basado en pórticos de hormigón, estos se encuentran rellenos en su mayoría por mampostería no confinada, la cual provoca un comportamiento estructural diferente al que se obtendría si se considera solamente el aporte de los pórticos; el sistema de entrepiso está basado en losas macizas de hormigón donde se encuentran las vigas embebidas.
Esta tipología presenta predominantemente una falla frágil en la base de las columnas toda vez que las mamposterías alcanzan su capacidad límite ante la solicitación sísmica, debido a la baja relación de rigidez entre vigas y columnas, la reducida capacidad a cortante de las secciones y la distribución irregular de mamposterías en planta, según indica Celi & Pantoja (2017).
Se puede atribuir este comportamiento también a las consideraciones tradicionales de que el pórtico estructural es la cual gobierna el comportamiento global de la estructura, cuando realmente es la mampostería que tiene una gran influencia en el resultado final de desempeño estructural.
En la Figura 1, se puede observar algunas de las variaciones de los modelos matemáticos que fueron realizadas. Se colocó una distribución irregular de la mampostería con el fin de capturar los efectos de torsión en planta. Esta distribución obedece a parámetros aleatorios de colocación de los paneles de relleno, por lo que, luego de un proceso de filtrado se escogió las curvas que se apeguen a la realidad y presenten un comportamiento sin decaimientos de capacidad bruscos.
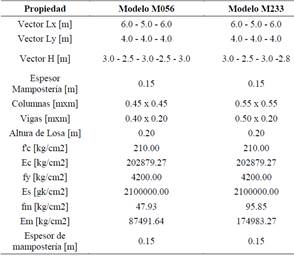
En la Tabla 1, se presentan las propiedades de los modelos 056 y 233 indicados en la Figura 1. Esta tabla muestra cómo se realizaron las variaciones de propiedades geométricas y mecánicas en las permutaciones generadas a partir de la información facilitada por el CAE-P. La distribución de las mamposterías obedece a un algoritmo aleatorio de colocación en planta y elevación, luego de este proceso se revisó cada modelo con el fin de conservar únicamente los que tienen una distribución similar a la que se utiliza en las estructuras reales.
Las demás permutaciones, fueron realizadas mediante la variación de los parámetros indicados en la Tabla 1 y principalmente mediante la colocación aleatoria de las mamposterías tanto en planta como en elevación.
La información que se presenta a continuación fue extraída de la documentación facilitada por el CAE-P y es utilizada como punto de partida para la realización de las permutaciones. Se extrajo las dimensiones de las columnas, vigas y losas y sus correspondientes armados, sin realizar comprobaciones sobre si estas cumplen con las normativas, ya que el propósito de la investigación fue determinar el estado actual de la tipología en cuanto a vulnerabilidad sísmica mediante curvas de fragilidad.
Las dimensiones de estas secciones fueron variadas para capturar de forma objetiva la mayor cantidad de permutaciones de la tipología analizada, con el fin de representar el comportamiento estructural bajo una perspectiva paramétrica; el proceso de determinación de permutaciones de tipología se indica más adelante.
4.1 Columnas
La información facilitada por el CAE-P muestra elementos columna con una sección igual en todos los pisos y en todas las columnas de la planta, por lo que, los modelos matemáticos seguirán esta tendencia. El armado de las columnas fue considerado como el 1% del área bruta de hormigón, distribuyéndolo simétricamente con varillas de 14mm y con un sistema de estribos que se compone de varillas de 10mm con gancho sísmicos a 135° cada 0.15 m de espaciamiento. De esta forma, se trata de modelar la incertidumbre de armado de columnas con experiencias previas de evaluación estructural y con la comprobación del desempeño sísmico que se ha evidenciado en el DMQ bajo las acciones sísmicas pasadas.
4.2 Vigas
En la investigación de Chicaiza (2017), se indica que las secciones de las vigas son embebidas en las losas, por lo que, para este trabajo las alturas de estas serán de la misma altura de la losa de hormigón armado.
4.3 Losas
El sistema de entrepiso fue considerado como una losa maciza de hormigón de 0.20 m de espesor, la cual permite establecer en el análisis que el piso entero tenga desplazamientos iguales en las direcciones horizontales ortogonales como un cuerpo rígido. No se ha considerado el armado de este elemento ya que el propósito no fue obtener la contribución de la capacidad de la losa, sino modelar la influencia de este sistema de entrepiso en la respuesta estructural global referente a efectos torsionales.
5. CONSIDERACIONES DE CÁLCULO
Para los modelos matemáticos generados no fue necesario considerar una viga tipo T como se lo realizó en las simulaciones de Pachano (2018) y Albuja & Pantoja (2017), ya que la estructura tridimensional provee la interacción entre la losa y la viga embebida mediante las consideraciones de piso rígido.
Se incluyó elementos verticales y horizontales elásticos con el fin de obtener estabilidad estática matemática, permitiendo la transmisión de cargas hacia la cimentación. Estos elementos fueron colocados en las zonas perimetrales de las mamposterías donde no existen elementos estructurales, como en las zonas de abertura de mampostería. Estos elementos no aportan rigidez lateral al sistema y tienen dimensiones de 0.20x0.20 [mxm]. De esta forma se obtuvieron propiedades dinámicas y de rigidez coherentes entre los modelos y la realidad del DMQ.
Como resultado de la investigación estadística de Parra & Sarango (2016), se concluyó que la ecuación simplificada para determinar el periodo fundamental aproximado de 152 edificios de hormigón armado, regulares y no adosados del DMQ es la ecuación (1).
Como ejemplo, se indica que para el modelo 003 de esta investigación, que posee una altura de 12.5 [m], esta ecuación resulta en 0.245 [s] como periodo en la dirección longitudinal y 0.277 [s] para la dirección transversal. Por otro lado, la ecuación de la NEC (NEC-SE-DS, 2015) que se muestra en la ecuación (2), con 𝐶 𝑡 =0.055 y 𝛼=0.9, resulta un valor de 0.534 [s] para el mismo modelo 003, el cual no refleja la realidad de las edificaciones medidas en el estudio de Parra & Sarango (2016).
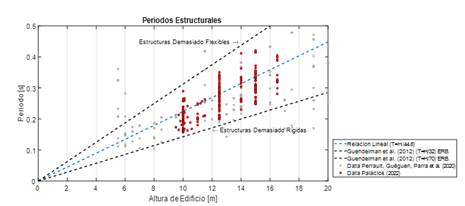
En esta investigación, no se realizó ninguna toma de datos para la calibración del periodo estructural mediante ensayos de vibraciones ambientales, ya que el propósito fue realizar un análisis que permita absorber la variabilidad de toda la tipología en cuanto a materiales, secciones y geometría. Si se comprobó que las relaciones de rigidez y masas sean consistentes con la realidad del DMQ, comparando los periodos elásticos teóricos con los ensayados y tabulados por Perrault et al., (2020), con el fin de permanecer en un rango aceptable para la caracterización de los modelos realizados, considerando la variabilidad introducida en la modelación estructural. Estos resultados se muestran en la Figura 2.
6. CURVAS DE CAPACIDAD
Con los modelos calibrados y ajustados a la realidad de la ciudad mediante la selección de curvas que no tengan caídas repentinas de capacidad y eliminación de modelos estructurales que presentan distribuciones de mamposterías no convencionales, se procedió a calcular las curvas de capacidad de los modelos evaluados, escogiendo la máxima, media y mínima como indica la Figura 3. Se pueden observar también las curvas de capacidad de todas las permutaciones aceptadas para las tipologías de cuatro (4), cinco (5) y seis (6) pisos considerando el análisis de distribución de fuerzas según el modo fundamental de vibración.
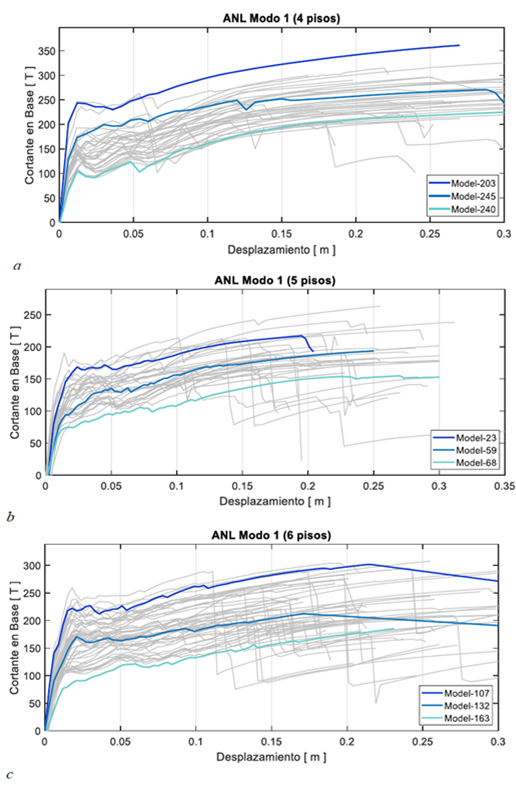
Figura 3 Curvas de capacidad máxima, mínima y media para análisis de distribución de fuerzas según primer modo de vibración. a) Variación cuatro pisos. b) Variación de cinco pisos. c) Variación de seis pisos.
Con la consideración de cálculo de curvas de capacidad obtenidas mediante las demás distribuciones de fuerzas planteadas y los resultados de las curvas máximas, medias y mínimas, se puede proponer los umbrales de daño que se indican en la
Tabla 2, estos fueron determinados mediante un análisis punto a punto de las curvas de capacidad y la evaluación de cuando se alcanzó un nivel de desempeño que caracterice al umbral de daño seleccionado. Estos umbrales de daño fueron basados en el desplazamiento último du que es caracterizado por el estado de daño “Completo”, el estado de daño “Extensivo” y “Moderado” son caracterizados por un sistema de rotulación en elementos estructurales con desempeños cercanos al colapso y seguridad de vida, según lo especificado en las tablas del ASCE 41 (2017). Finalmente, el estado de daño “Leve” fue caracterizado cuando las edificaciones alcanzaron el límite de fluencia en sus elementos estructurales.
7. ESPECTROS DE PELIGRO SÍSMICO
Según Celi et al. (2016), el evento de 475 años de periodo de retorno es el evento sísmico de demanda para la filosofía de diseño sismorresistente ecuatoriana y el evento de 100 años de periodo de retorno es uno de los eventos sísmicos más probables dentro de la sismicidad histórica Quiteña, por lo que estos escenarios son considerados como límites en los intervalos de intensidades. Se realizaron variaciones al periodo de retorno para obtener diferentes valores de Z de la curva de peligro sísmico de Quito y el resultado de todos estos espectros se indica en la b
Figura 4.
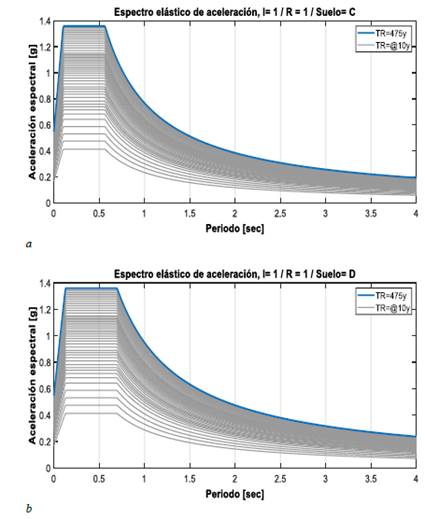
Figura 4. Variación de intensidades en espectro de respuesta de la NEC-SE-DS (2015). a) Suelo tipo C. b) Suelo tipo D
Con la variación de intensidades seleccionadas y que definen la forma espectral en la NEC-SE-DS (2015), se procede a encontrar los puntos de intersección entre el espectro de demanda y el espectro de amenaza en un espacio de coordenadas espectrales conocido como ADRS (Acceleration Displacement Response Spectra) por sus siglas en inglés y de esta forma el punto teórico de intersección entre espectro de capacidad y de demanda, aportan su contribución para la determinación de la fragilidad estructural.
8. PUNTOS DE INTERSECCIÓN ENTRE ESPECTRO DE CAPACIDAD Y ESPECTROS DE AMENAZA
Conceptualmente, el método de espectro de capacidad es un procedimiento de análisis estático no lineal que utiliza la intersección de la curva de capacidad y el espectro de respuesta reducido en un sistema de coordenadas común para calcular el desplazamiento máximo. La representación gráfica de esta intersección proporciona una idea clara de cómo la edificación responderá al movimiento del terreno por las fuerzas de origen sísmico y este fue considerado como el parámetro de medición dentro del desplazamiento espectral (Martinez, 2012).
En esta investigación, la selección del tipo de estructura bajo el ATC40 (1996) supone que la tipología 4 debió cumplir ciertos requerimientos dados por la normativa vigente en el tiempo de construcción, pero esto no significa que la tipología posea un comportamiento con una buena disipación de energía debido a varias consideraciones, como que el código de construcción utilizado no refleja los avances de investigación en cuanto a buen comportamiento estructural que se manejan hasta la fecha actual, existe alta incertidumbre en la definición de las capacidades de los materiales estructurales y el armado que se realizó in situ y finalmente, se desconoce si existió algún control en obra. Por este motivo, se maneja una comportamiento estructural medio según las especificaciones del ATC40 (1996), es decir uno Tipo B.
El punto teórico encontrado puede darse en el rango elástico del espectro de capacidad y este resultado puede ser interpretado de dos formas, ya que la demanda del sismo es pequeña y permite que la estructura tenga aún un comportamiento elástico, o que la estructura es bastante resistente y puede mantenerse en el rango elástico para el nivel de intensidad de la solicitación (Silva, 2018). Entendiéndose que el método especificado en el ATC40 (1996) para el grupo tipológico B puede concluir en bajas ductilidades por desplazamiento de la edificación en análisis, y esto no es coherente con la realidad visible de la tipología analizada, es necesario realizar una revisión de los resultados obtenidos especialmente para intensidades altas.
Los resultados obtenidos permitieron ejecutar el algoritmo de simulación de Monte Carlo, el cual necesita la información de entrada que son los valores de la variable de control, en este análisis se utilizó los desplazamientos espectrales obtenidos como resultado de la intersección de los espectros de capacidad con los de demanda como variable de control. Dado que para cada umbral de daño existen límites de desplazamiento, el algoritmo de Monte Carlo realiza varias simulaciones en este rango de desplazamientos hasta encontrar la función de distribución normal que permita caracterizar la fragilidad estructural.
9. RESULTADOS
Las curvas de fragilidad se definen mediante la ecuación (3), esta permite agrupar distintos niveles de desempeño representados en desplazamiento espectrales determinados ante distintos niveles de amenaza sísmica.
Donde:
La ecuación (3) asume las siguientes hipótesis:
1) En los desplazamientos espectrales que pertenecen a los umbrales de daño calculados, la probabilidad de que se iguale o exceda el estado de daño es del 50%.
2) Las frecuencias de los diferentes resultados generados por esta simulación resultan en una distribución normal, por este motivo se puede definir el resultado mediante la media y la desviación estándar para describir como varían los resultados.
Se tomaron todas las curvas de fragilidad obtenidas para los modelos de cuatro (4), cinco (5) y seis (6) pisos que resultaron con las curvas de capacidad máximas, media y mínimas para un determinado tipo de suelo. Luego de esto, se encontró la media matemática de todas esas curvas para representar la curva final de fragilidad, esto se muestra en la en la Figura 5.
Se incluyó un valor de +- 0.5 desviación estándar con el fin de caracterizar las curvas de fragilidad de forma probabilista cuando se superen o igualen los límites de daño, aportando un valor de confiabilidad dado por la función de distribución normal. Este valor de desviación estándar adoptado demostró ser suficiente para los objetivos de la investigación, ya que utilizar valores de mayor magnitud resultan en una redundancia matemática de probabilidad de sucesión de eventos del 0 al 100%, perdiendo así el propósito de la investigación, como se indica en los resultados de la Figura 5.
Las curvas de fragilidad finales para la representación de la vulnerabilidad sísmica de la tipología 4 se muestran en la Figura 6 para el suelo tipo C, expresadas mediante la media (x̄) y la desviación estándar (σ). En el fondo, se pueden observar todos los resultados obtenidos que se describieron en la Figura 5. También se puede observar que se han graficado parámetros de control adicionales como los desplazamientos espectrales que resultan de la intensidad para movimiento ligero, medio y fuerte, estos corresponden a derivas globales de piso de 0.5%, 1.0% y 2.0% de la altura, respectivamente.
Se realizó el mismo procedimiento de caracterización de las curvas de fragilidad para el suelo tipo D, estos resultados se muestran en la Figura 7, expresados mediante la media (x̄) y la desviación estándar (σ).
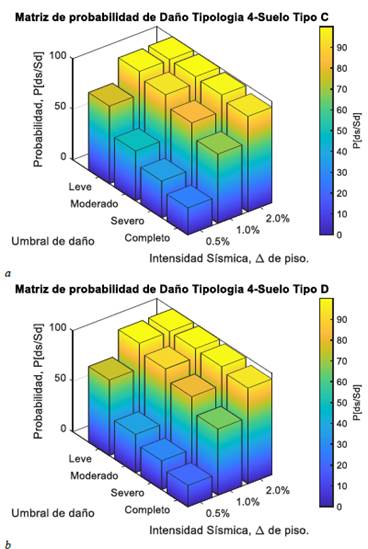
Finalmente, se presentan los resultados de las matrices de probabilidades de daño para la envolvente media para los tipos de suelos C y D en la Figura 8, respectivamente.
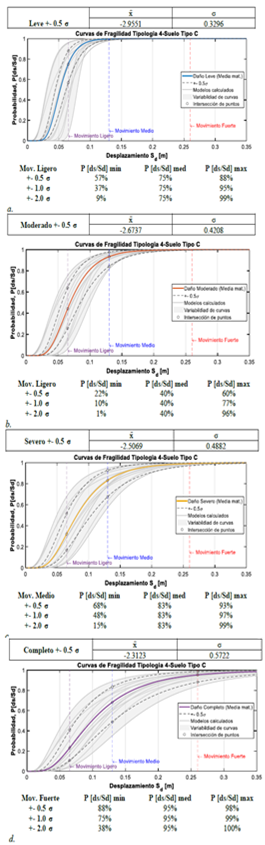
Figura 5. Curvas de fragilidad y resultados para envolvente máxima. Suelo tipo C. Daño a) Leve. b) Moderado c) Severo. d) Completo
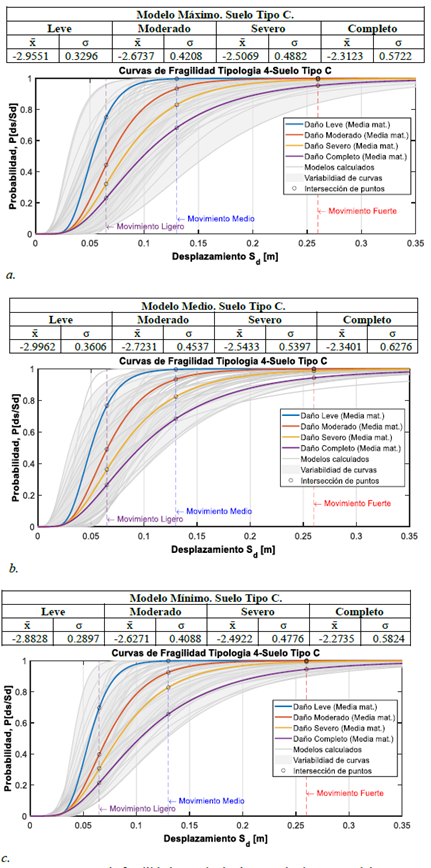
Figura 6. Curvas de fragilidad para tipología 4. Suelo tipo C. Modelo con curva de capacidad. a) Máxima. b) Media. c) Mínima
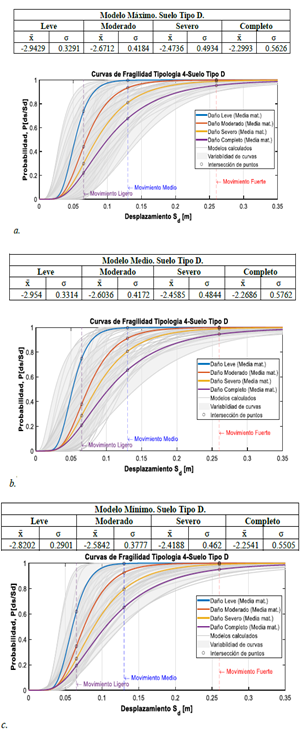
Figura 7. Curvas de fragilidad para tipología 4. Suelo tipo D. Modelo con curva de capacidad. a) Máxima. b) Media. c) Mínima
10. CONCLUSIONES
Los modelos realizados fueron validados a nivel de masas y rigidez mediante la comprobación de los periodos elásticos y su rango de variabilidad en el DMQ definido por los intervalos de 0.15 a 0.35 [s], por lo que el modelo adoptado de mampostería genera resultados estables y adecuados en cuanto a comportamiento modal de las edificaciones analizadas.
Debido a la alta sensibilidad de la función de distribución que resulta del método al punto teórico de colapso du, en las curvas de capacidad, este debe ser definido mediante un análisis controlado por fragilidad local dentro del análisis estático no lineal.
Los umbrales de daño que se utilicen para la definición de las curvas de fragilidad deben ser calculados a partir de las propiedades intrínsecas de la tipología estructural analizada y no deben ser generalizados a partir de otros estudios.
Aunque se haya utilizado un enfoque probabilista y una disminución de la incertidumbre por la alta cantidad de modelos matemáticos creados, la naturaleza del problema global es altamente no lineal, por lo que no es posible garantizar un nivel alto de confianza de la respuesta obtenida. Este es el motivo por el que se manejan probabilidades del 50% de que se igualen o se excedan los límites establecidos en las curvas de fragilidad.
El valor asignado de 0.5 desviación estándar, fue suficiente para representar de forma razonablemente coherente los rangos de ocurrencia de igualación o superación de los umbrales de daño definidos por las curvas de fragilidad, este valor supone un valor de confiabilidad del 65% contenido en el percentil 60.
Los resultados mostraron que para derivas globales del 0.5% de la altura de la edificación, la tipología analizada presentó probabilidades entre el 62% y el 75% de igualar o exceder el límite de daño leve, entre el 35% y el 44% de igualar o exceder el límite de daño moderado, entre el 25% y el 36% de igualar o exceder el límite de daño severo y entre el 19% y el 27% de igualar o exceder el límite de daño completo.
Se observó que para derivas globales 1.0% de la altura de la edificación, la tipología analizada presentó probabilidades predominantes del 100% de igualar o exceder el límite de daño leve, entre el 91% y el 93% de igualar o exceder el límite de daño moderado, entre el 79% y el 83% de igualar o exceder el límite de daño severo y entre el 65% y el 68% de igualar o exceder el límite de daño completo.
Las curvas de fragilidad muestran que para un control basado en la deriva máxima permitida por la Norma Ecuatoriana de Construcción del 2%, se presentaron probabilidades predominantes del 95% de igualar o exceder el límite de daño completo.
La vulnerabilidad sísmica determinada a partir de las curvas de fragilidad, para el punto de intersección entre el espectro de capacidad y el de amenaza para un periodo de retorno de 475 años, se encuentra de forma predominante en los estados de daño de moderado y severo.
Los resultados obtenidos por el análisis de fragilidad mostraron que considerar los efectos de torsión en planta, provocado por la distribución irregular de las mamposterías, resulta en mayores probabilidades de exceder límites de daño en comparación a modelos estructurales con distribución regular de mampostería, por lo que la hipótesis planteada se cumplió.
Las altas probabilidades que se encontraron para exceder el límite de daño completo en la tipología analizada concluyen en los impactos de índole económico debido al costo de reposición de las edificaciones, la paralización de actividades en los sectores afectados y la vida social de los damnificados.