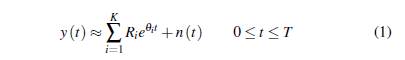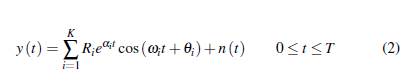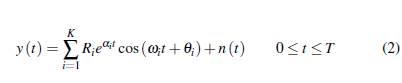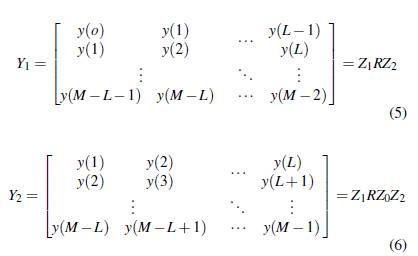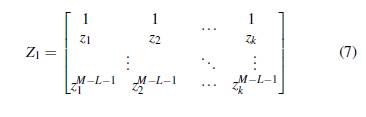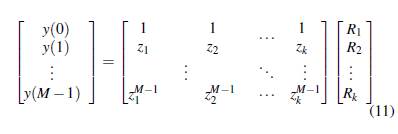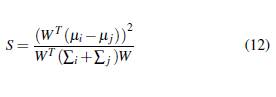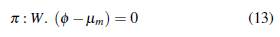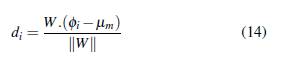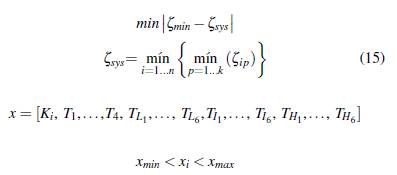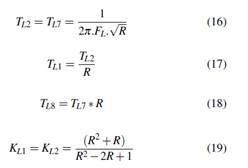INTRODUCCIÓN
Los estabilizadores del sistema de potencia son dispositivos de control ampliamente utilizados para amortiguar las oscilaciones electromecánicas de baja frecuencia del sistema eléctrico de potencia (SEP), los cuales proporcionan una señal adicional al regulador automático de voltaje (AVR). Las oscilaciones electromecánicas se presentan en el rotor del generador debido principalmente a la dinámica cuasi-estacionaria del sistema dado. Algunos de los factores que producen estas oscilaciones son las variaciones continuas de carga y/o generación y la ocurrencia de grandes perturbaciones o fallas en el sistema (Mondal et al., 2020). Esta situación conlleva a que la señal de velocidad de rotor actúe como una señal de entrada al PSS, con la finalidad de sensar las condiciones operativas del sistema.
El análisis de la estabilidad de pequeña señal en los sistemas eléctricos modernos permite identificar la presencia de modos de oscilación críticos, cuya frecuencia compleja tenga una parte real positiva (oscilaciones crecientes) o sean poco amortiguados (parte real negativa, pero de pequeña magnitud) en la operación del SEP. El análisis de estabilidad de pequeña señal en los sistemas eléctricos modernos permite identificar la presencia de modos de oscilación críticos. En particular, la frecuencia oscilatoria compleja en la opera- ción del SEP puede estar constituida por una parte real positiva (oscilaciones crecientes) o una parte real negativa de pequeña magnitud (poca amortiguación). En el escenario en que las oscilaciones no son debidamente amortiguadas luego de una condición particular de operación, se procede a la desconexión de elementos o incluso al colapso del SEP (, ).
() y () clasifican a los modos de oscilación por su frecuencia y el área del sistema en los que son observados, lo cual determina su característica local o global. Específicamente, los modos de oscilación local ocurren entre generadores de una misma área; estos se caracterizan porque las máquinas oscilan unas contra otras, y su rango de frecuencia típico es del orden de 0.7 a 3 Hz. Los modos de oscilación interárea se producen por las oscilaciones de un grupo de generadores de un área del sistema respecto a otra área interconectada a través de líneas que se hallan por lo general congestionadas, siendo su rango típico de frecuencia de 0.1 a 0.7 Hz. Las características de estos modos son complejas y diferentes a aquellas descritas para los modos locales. Este tipo de modos no son tan observables y son difíciles de controlar por medio de PSSs convencionales.Por lo que, es necesario el desarrollo de PSSs que cuenten con un bloque dedicado para este tipo de bajas frecuencias (p.ej., PSS4B denominado multibanda) (, ) y que sus parámetros sean sintonizados de manera que se adapten a la condición operativa del sistema (, ).
Si bien, en la literatura existe una amplia variedad de artículos que analizan el impacto del PSS para mejorar la estabilidad del SEP, a través de diferentes herramientas clásicas de control (, ) o métodos de optimización (, ). Sin embargo, las propuestas de métodos de sintonización adaptativa son aún escasas al tener en consideración la disponibilidad tecnológica inherente en el PSS multibanda.
Además de la disponibilidad tecnológica es necesario considerar que existen muchos generadores operativos que disponen únicamente de PSSs convencionales. Cabe mencionar que, la capacidad de amortiguamiento del PSS es limitada a la parametrización fija especificada por el mismo y el hecho de considerar reemplazarlo con un PSS4B conllevaría retos técnicos y/o económicos adicionales, como por ejemplo, adquisición, instalación y una adecuada parametrización, lo que muchas veces vuelve inviable este tipo de proyectos. En estos casos, alternativas de sintonización adaptativas aplicadas a PSSs convencionales resultan atractivas para a ser consideradas.
Por otro lado, es necesario resaltar que en el estado del arte no se han realizado comparaciones de la sintonización de los PSSs convencionales que incluyan el uso de técnicas adaptativas con la respuesta del PSS4B, el cual es diseñado para adaptarse de forma natural a un amplio rango frecuencial, es decir, el amortiguamiento obtenido con el PSS4B se caracteriza por manejar bandas de frecuencia para monitorear a los diferentes modos de oscilación. Con base a lo descrito previamente, el presente artículo analiza y presenta una estrategia de sintonización para los PSSs existentes en un sistema, considerando un esquema adaptativo mediante la determinación de los modos críticos de las señales de potencia y frecuencia disponibles en el sistema de monitoreo de área amplia (WAMS). Para tal propósito, se utiliza la metodología de la matriz Pencil para la identificación modal de una señal del sistema y la aplicación de árboles de decisión para la selección de los parámetros del PSS en cada uno de los subespacios operativos.
2. SINTONIZACIÓN ADAPTATIVA DE PSS CONVENCIONALES
2.1 Identificación Modal de Sistemas Eléctricos de Potencia
En general, el análisis modal es una herramienta que permite considerar el modelo dinámico de un SEP representado en espacio de estado por ecuaciones algebraico-diferenciales y usadas en el software de simulación. Sin embargo, este tipo de simulación no puede ser realizada en tiempo real por sus limitaciones relacionadas al tiempo computacional demandado. Por lo tanto, es interesante explotar la capacidad de extraer la información modal directamente de las señales eléctricas disponibles en el sistema WAMS. En este contexto, se han propuesto varios métodos para extraer la información modal de señales que varían en el tiempo, siendo el método de la matriz Pencil ampliamente utilizado en la literatura. Este método permite determinar las frecuencias y el nivel de amortiguamiento de la señal analizada, en un tiempo de procesamiento inferior a otros métodos tales como el Prony. En particular, el enfoque de la matriz Pencil demanda de pocos segundos para el procesamiento de un gran volumen de datos (, ; , ).
Además, el método de la matriz Pencil ajusta los datos del sistema WAMS obtenidos en un tiempo de muestreo uniforme a una suma de funciones exponenciales. Específicamente, la amplitud, la frecuencia y el nivel de amortiguamiento son los parámetros obtenidos de las señales monitoreadas de la condición operativa del SEP. En la Ecuación (), se muestra la representación matemática de la estimación modal (, ).
Donde y(t) es la señal registrada por el WAMS. Ri es la amplitud mientras que θ i es la fase del i-ésimo modo, el mismo que tiene un nivel de amortiguamiento α i con una frecuencia compleja jω i que representan los valores propios de la matriz de estado A del sistema. Así mismo, t es el tiempo de muestreo de los datos, K es el número de modos a ser estimados, T es el tiempo total de muestreo y n(t) es el posible ruido de los datos.
La señal y(t) puede representarse como en la Ecuación () de acuerdo a lo establecido en ().
El algoritmo de la matriz Pencil busca encontrar los mejores R i , θ i y z i = e (α i + jwit) para el total de muestras analizadas en el periodo T. En una primera instancia, se determinan los z i que representan los valores propios de la entidad matemática estructurada a través de la combinación de las matrices Y 1, Y 2. El parámetro escalar λ como se plantea en la Ecuación () es conocido como la matriz Pencil. Cada matriz se forma utilizando los valores muestreados de y(t). En la segunda etapa, utiliza los z i encontrados para estimar las amplitudes
R i y ángulos de fase θ i resolviendo un problema de mínimos cuadrados (, ).
Los M datos de la unidad de medición fasorial (PMU) que conforma el sistema WAMS, son organizados a través de una matriz Hankel como se establece en la Ecuación () (, ; , )
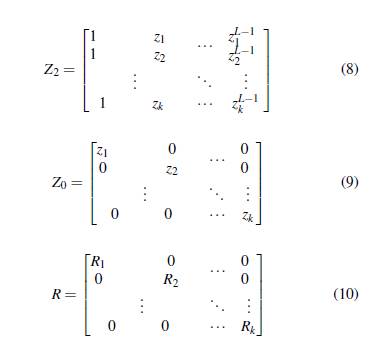
Donde, L se conoce como el parámetro de Pencil, el cual puede ser seleccionado arbitrariamente en el intervalo [ M 3 , M 2 ] a través del cual se crean las submatrices Y 1 de la Ecuación (5) y Y 2 de la Ecuación (6) (Trinh et al., 2019). De acuerdo con Crow (2016), al considerar la Ecuación (1) y Ecuación (2) es posible construir las matrices Y 1 y Y 2 en función del R i y z i como:
Donde:
Una vez determinadas las matrices, es posible calcular la magnitud de la componente exponencial de la Ecuación () al resolver la Ecuación () (, ). Por lo que, se obtiene:
2.2 Adaptabilidad del PSS por medio de árboles de decisión
El algoritmo de árbol de decisión forma parte de las llamadas máquinas de aprendizaje. En nuestra propuesta, los árboles de decisión utilizados se basan en una partición del conjunto de datos en los denominados subespacios basado en variables de frecuencia y potencia del sistema WAMS. Con la ayuda de estas variables se puede establecer árboles de clasificación para la condición operativa a ser analizada. Posteriormente, el clasificador permite establecer para una nueva condición operativa del sistema el conjunto de parámetros del PSS determinados en cada subespacio, a lo cual en el estudio se denominan árboles de regresión.
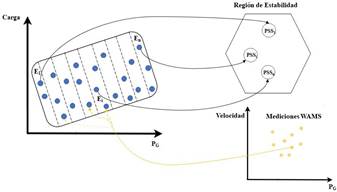
Los árboles de clasificación posibilitan determinar las reglas de partición de cada subespacio, mientras que con los árboles de regresión identifican el subespacio a cuál corresponden las variables de interés bajo análisis. La operación diaria de un sistema eléctrico se relaciona con las variaciones en las condiciones operativas. En la Figura , se muestra la esquematización de la división en varios subespacios (E i ) , los cuales son determinados a través de las condiciones operativas (generación y carga) por medio del clasificador establecido por el árbol de decisión. Para el caso de un nuevo grupo de datos obtenidos desde el sistema WAMS, se aplica el árbol de
regresión con el cual se determina el subespacio al que pertenecen estos datos. Finalmente, se selecciona el conjunto de parámetros con los que son sintonizados los PSSs.
La estructuración del árbol de decisión para las etapas de clasificación y regresión requiere del monitoreo de múltiples condiciones de operación del SEP para evaluar la dinámica de los modos de oscilación presentes en la condición operativa del sistema. De esta manera, los PSSs pueden ser presintonizados fuera de línea mediante múltiples condiciones de operación y sus parámetros pueden ser modificados de forma adaptativa. La modificación depende del subespacio que sea determinado por el árbol de regresión al utilizar las mediciones del sistema WAMS en línea. Es decir, el árbol de decisión permite identificar el subespacio de interés para determinar qué conjunto de parámetros de los PSSs es el óptimo para las condiciones operativas monitoreadas en ese instante de tiempo.
() presenta el proceso de clasificación para el árbol de decisión, el mismo que comienza desde el nodo raíz superior y en cada nivel los subconjuntos se dividirán de acuerdo con las reglas de división óptimas. Las reglas de división son de la forma “si- entonces-que”. Para el caso de estudio en este documento, cada nodo terminal representa un subespacio de la condición de operación, determinada por la potencia y la frecuencia de la barra de los generadores de interés. El conjunto de datos de operación contiene múltiples mediciones (p.ej., para el caso de análisis se utiliza m i y m j ).
En cada grupo de datos, se puede obtener la media µ y la covarianza ∑ de las mediciones. Así, la división óptima entre las diferentes clases del grupo de datos (que representan múltiples mediciones de la operación), hace posible establecer una línea de clasificación entre los mismos. Para el caso de contar con más de una medición se establece un hiperplano en lugar de una línea, donde para cada hiperplano es posible determinar un vector normal W , el cual establece la mayor varianza entre cada grupo. Con este proceso se construye la regla de clasificación S mediante la maximización de la diferencia entre las clases de los datos de acuerdo a la Ecuación
() (, ).
A partir de la Ecuación (), es posible determinar la distancia de cualquier punto de operación del hiperplano, mediante el vector φ compuesto por los puntos de operación respecto a los puntos medios de cada grupo. De esta forma, se determina el hiperplano π, de acuerdo con la Ecuación ().
Mediante la Ecuación (), el vector φ i = (x i , y i , ...) permite determinar la distancia del punto de operación clasificado en el subespacio E i al hiperplano π en base a la Ecuación ().
Donde d i es la variable de entrada para el árbol de decisión por medio del cual se realiza el proceso de clasificación para determinar las reglas de división de subespacios. Al establecer estas reglas, se puede llevar adelante el proceso de regresión, con el cual se logra identificar el subespacio al que pertenece el punto operativo analizado.
3. PROPUESTA DE AMORTIGUAMIENTO DE LAS OSCILACIONES CON PSS
3.1 Esquema de control adaptativo del amortiguamiento con PSSs convencionales instalados en el sistema
Como se indicó anteriormente, los PSSs existentes en el SEP son de tipo convencional ya sean los denominados PSS1A o PSS2B. El instalar en el sistema un PSS tipo PSS4B (cuyas características se explican más adelante) representa retos técnicos y gastos económicos-financieros adicionales. Específicamente, la adquisición del equipo, así como su instalación e implementación de una adecuada sintonización. Por lo que, los proyectos relacionados con este reemplazo tecnológico por lo general no suelen ser viables. En vista de lo indicado, el esquema de control adaptativo busca mantener la estabilidad oscilatoria haciendo uso de la funcionalidad de los árboles de decisión aplicado a las mediciones de frecuencia y potencia monitoreadas en el sistema WAMS. Con este proceso, se determinan adaptativamente los parámetros de los PSSs según sean las condiciones de operación del sistema.
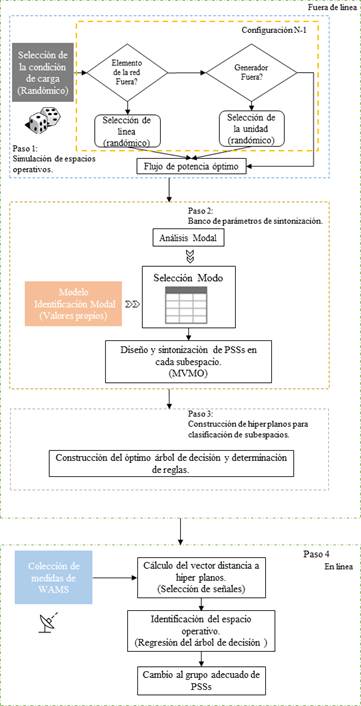
En este trabajo, se propone la metodología de cuatro etapas, como se muestra en la Figura . El proceso de sintonización adaptativa, inicia con una sintonización coordinada de los PSSs realizada fuera de línea. En la primera etapa, el universo operativo del sistema de potencia se divide en diferentes subespacios operativos de acuerdo con la condición de carga, la cual es variada a través de una simulación de Montecarlo. En la segunda etapa, para cada subespacio, se determinan, mediante análisis modal, los modos de oscilación críticos de la condición operativa (si es una condición de operación viable obtenida mediante un flujo de potencia óptimo), para cada modo crítico se calculan los residuos a través de los cuales es se selecciona el PSS del generador i-ésimo a ser activado.
Con lo indicado anteriormente, se selecciona el PSS del i-ésimo generador a través del residuo del k-ésimo modo y en conjunto con el nivel de amortiguamiento deseado. De esta forma, se determina la función objetivo del problema de optimización planteado mediante la Ecuación (). La solución del problema se obtiene por medio del algoritmo heurístico mapeo media-varianza (MVMO) ( , ). Con este enfoque, se determina el conjunto de parámetros óptimos para la sintonización de los PSSs para cada subespacio de operación. Matemáticamente, el problema de optimización es planteado como:
Donde ζ min es el nivel mínimo de amortiguamiento alcanzado por el sistema, ζ sys es el nivel de amortiguamiento mínimo deseado para el sistema (en el estudio se establece como límite 10 %). Mientras que, x es un vector que contiene los diferentes parámetros de los PSSs (ganancias y constantes de tiempo), dentro de los límites correspondientes.
El algoritmo heurístico MVMO permite obtener los parámetros óptimos de sintonización de los PSSs, a través de los cuales se busca alcanzar la menor desviación del nivel de amortiguamiento presente en el sistema respecto al nivel de amortiguamiento deseado. En cada iteración, el algoritmo incrementa el nivel de amortiguamiento de los modos de oscilación por el cambio de parámetros de los PSSs seleccionados por medio del residuo para la condición operativa analizada. Para estos escenarios, es necesario considerar que los parámetros determinados para los PSSs seleccionados se almacenan en cada subespacio que representa múltiples condiciones operativas.
En la tercera etapa, se construye el modelo de hiperplanos para la clasificación de los subespacios, estableciéndose las reglas de división del árbol de decisión óptimo. La cuarta etapa corresponde al uso de la información del sistema WAMS junto con los resultados de la identificación modal realizada por medio de la matriz Pencil, la cual es seleccionada en conjunto a los parámetros de los PSS. La regresión determina a qué nodo terminal del árbol de decisión (subespacio) del punto de operación corresponde el estado operativo actual del sistema.
De esta forma, el algoritmo propuesto activa y determina los parámetros de los PSSs de cada subespacio clasificado mediante el árbol de decisión. En este punto, es necesario indicar que, el sistema WAMS permite el envío en línea de comandos remotos, facilitando realizar en línea la actualización de los parámetros de los PSSs, a través de modulación de señales (, ). Este escenario descrito no es abordado en el presente documento, por lo que, se asume que en la simulación los parámetros de sintonización del PSS se actualizan de manera automática.
3.2 Algoritmo heurístico MVMO
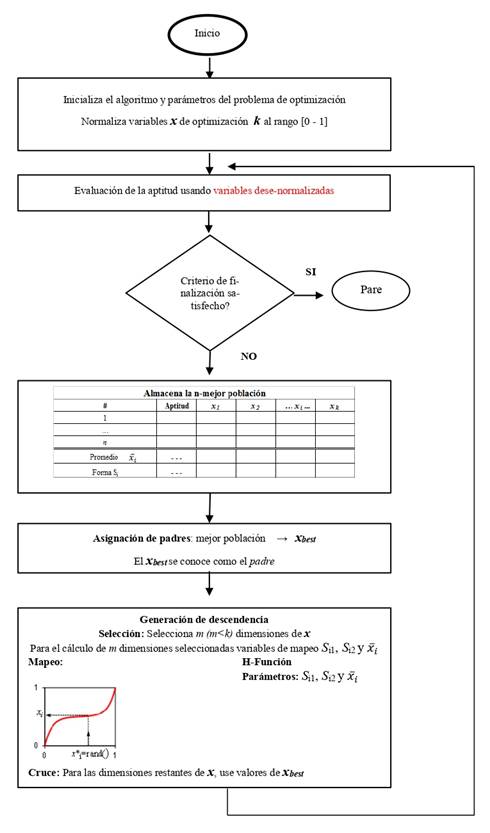
El algoritmo de optimización de mapeo de media varianza pertenece a los métodos de optimización heurística basados en el comportamiento poblacional, tal como se presenta en la Figura . En particular, en este método, se establece una función de mapeo a través de la media y varianza de la mejor población alcanzada en cada iteración (p.ej., en general constituida como máximo por los cinco mejores individuos) mediante la evaluación de la función objetivo del problema analizado. Este proceso en cada iteración permite mutar la población entre los mejores individuos. Una condición necesaria en el algoritmo es normalizar las variables a optimizar en el rango [0,1] con lo cual se garantiza que la solución sea dentro de sus límites [min., máx.]. Mediante este mecanismo de control de la descendencia a través de la función de mapeo a lo largo del proceso de búsqueda, permite al algoritmo MVMO alcanzar una ponderación entre su diversificación y la cantidad de individuos en la búsqueda de la solución óptima, situación que se traduce en un comportamiento de rápida convergencia con mínimo riesgo de convergencia anticipada del algoritmo (, ).
3.3 PSS Multibanda
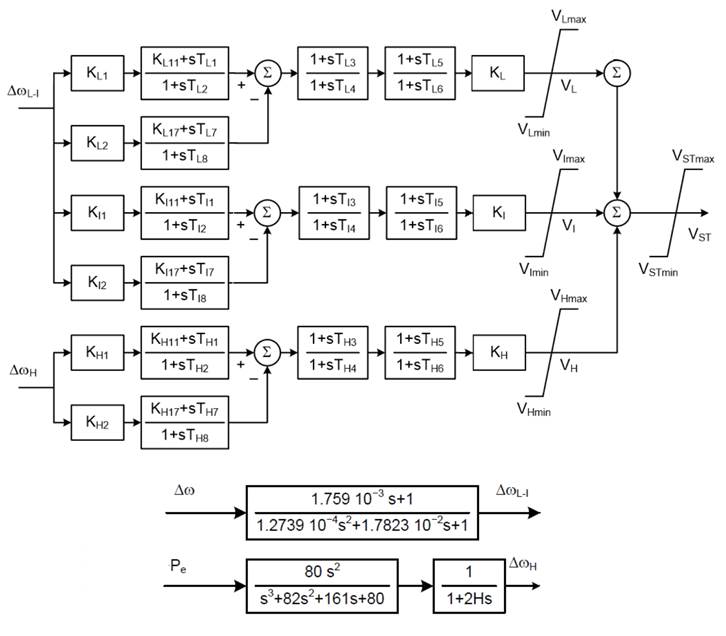
En esta sección, se presentan las bondades del PSS multibanda, el cual fue propuesto en virtud de los diferentes rangos de frecuencia de los modos de oscilación existentes en un sistema eléctrico. Las oscilaciones no pueden ser compensados de forma simultánea por un PSS convencional con parámetros fijos. Así, este tipo de PSSs se estructura en tres bandas, a saber, baja, media y alta frecuencia. Estas bandas permiten monitorear los modos de oscilación del sistema, de este modo, la salida de cada una de las bandas es sumada para formar la señal de salida final del PSS. Todo este mecanismo, permite al PSS multibanda realizar una compensación de fase dentro de un mayor rango frecuencial de los diferentes modos críticos presentes en el sistema de potencia. Este proceso hace posible incrementar el amortiguamiento del sistema.
En la Figura , se presenta la modelación del PSS multibanda (, ).
Donde:
T b corresponde a las diferentes constantes de tiempo de la estructura del PSS multibanda de la Figura 4.
K b denota las diferentes ganancias de la estructura del PSS multibanda de la Figura 4.
Además, en la Figura se observa la estructura del PSS4B implementada en PowerFactory, la cual permite analizar los rangos de frecuencia, denotados como: baja (L) de 0.01-0.1 Hz, intermedia (I) de 0.1-1 Hz y alta (H) de 1-4 Hz. En (), se presenta un conjunto de datos típicos para la sintonización de este tipo de PSS, como ejemplo, para el caso de la banda baja se presentan las ecuaciones () a (). En estas expresiones en las cuales se considera el parámetro R=1,2 que muestra ser el de mejor respuesta, tal como lo identificó (). Finalmente, el procedimiento de sintonización de esta clase de PSSs, se orienta a alcanzar una amortiguación óptima para las distintas frecuencias.
4. SISTEMA DE ESTUDIO Y ANÁLISIS DE RESULTADOS
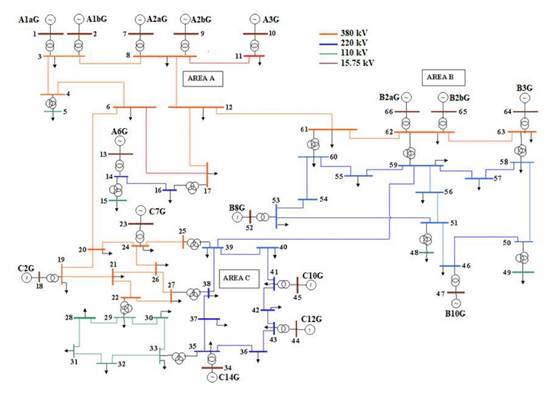
La metodológica propuesta se aplica al sistema eléctrico New York-New England que consta de tres áreas fuertemente malladas, 66 barras, 16 generadores, 28 transformadores, 52 líneas de transmisión, las cargas se consideran de potencia constante. El diagrama esquemático del SEP se ilustra en la Figura , donde las constantes de tiempo T w y T w1 se consideran de 10 segundos. Además, para cada subespacio se realiza el análisis eléctrico para determinar su factibilidad, a fin de cumplir adecuadamente, las condiciones operativas de voltaje y cargabilidad de elementos. Para la simulación dinámica del SEP se utiliza PowerFactory de DIgSILENT versión 15.1.7, software de ingeniería para estudios de flujo de potencia, estabilidad de pequeña señal y simulaciones en el dominio del tiempo. Este software en conjunto con herramientas desarrolladas en Python, permiten llevar adelante las diferentes etapas de la metodología propuesta.
Para considerar múltiples condiciones operativas, en el estudio se establece una variación de la carga en un 5 % y un evento en la línea BC debido a un cortocircuito trifásico ocurrido en 1 segundo de la simulación y despejado a los 1,1 segundos. Los resultados obtenidos mediante la simulación en PowerFactory, con un tiempo de muestreo de 0,01667s (similar al establecido en la PMU que presenta una tasa de muestreo de 60 muestras por segundo), permiten reproducir los registros de frecuencia y potencia que se obtendrían del sistema WAMS.
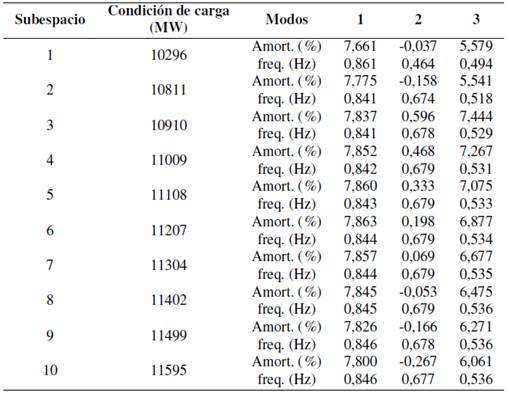
En cada subespacio, a través del análisis modal y la matriz Pencil para los registros en el dominio del tiempo, se determinan los modos críticos, como se muestra en la Tabla 1. Aquí, se presentan los modos obtenidos en el subespacio 3, apreciándose la alta similitud en los parámetros de los modos obtenidos por cada método. De esta forma, se verifica la eficacia de la matriz Pencil para estimar los modos oscilatorios a partir de señales del sistema. Por lo tanto, estos valores de frecuencia y nivel de amortiguamiento pueden ya ser usados en el proceso de clasificación en tiempo real.
En la Tabla 2, se observa como la variación de las condiciones operativas tienen impacto en los modos de oscilación. A partir de los datos presentados, note que existen tres modos críticos para cada subespacio. Los modos críticos están definidos como los valores propios que tienen un nivel de amortiguamiento menor al 10 %. Se observa que, en algunos subespacios el modo 2 se halla en la zona inestable (amortiguamiento negativo). Esta situación demuestra la necesidad de que el sistema cuente con PSSs y con una sintonización que se adapte a las condiciones operativas. En la etapa fuera de línea, el conjunto de aprendizaje para construir el árbol de clasificación es generado con 1000 simulaciones del sistema de prueba para cada subespacio, considerando las contingencias de manera estocástica. Así mismo, para el caso de 10 subespacios se determina una muestra de aprendizaje de 10000 simulaciones para el árbol de decisión.
El cambio de las condiciones operativas es monitoreado por el árbol y mediante esta información los PSSs se sintonizan para cada subespacio obtenido fuera de línea. Las medidas utilizadas para determinar los subespacios con el árbol de decisión son la frecuencia de la barra y la potencia del generador que presente el mayor residuo. Por medio del monitoreo de estas variables, se alcanza una mayor controlabilidad y observabilidad para cada modo de oscilación crítico. En este estudio, los generadores A 1aG , A 6G , B 10G , C 2G , C 7G y C 12G son los que presentan el mayor residuo.
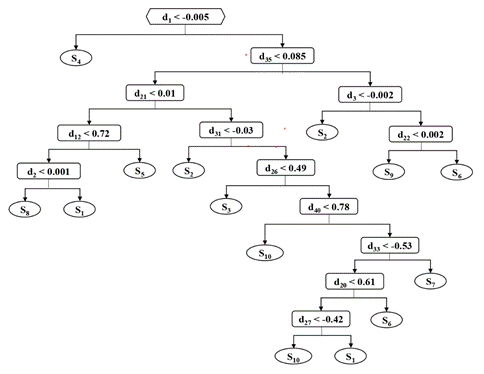
Debido al gran volumen de datos del modelo, se busca un compromiso en el tamaño del árbol de clasificación. Así, considerar uno de tamaño pequeño no permitirá capturar la dinámica del comportamiento del conjunto de datos. Por el contrario, uno de tamaño grande puede llevar a un sobre ajuste, situación que podría llevar a una incorrecta identificación de los subespacios ( , ). Por lo tanto, la selección de un tamaño adecuado del árbol determina la precisión de la clasificación. Para el presente estudio, el número óptimo del árbol de decisión es establecido en 10 subespacios por medio del cual se alcanza 0,0792 que representa una probabilidad de 92,1 % en la selección del subespacio correcto para la condición operativa analizada. La Figura muestra la estructura del árbol de decisión formado para el sistema de prueba analizado, en donde se establecen las reglas de división en cada nodo y se determinan 10 nodos terminales que representan los 10 subespacios de operación.
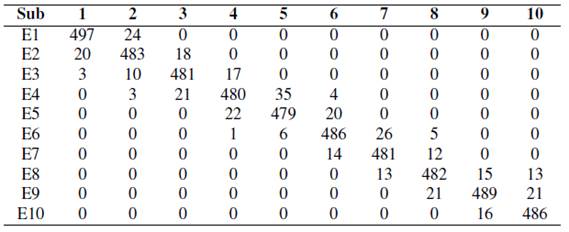
La metodología al calcular los modos oscilatorios de las señales, obtenidos de la condición operativa analizada, busca emparejar los mismos con aquellos modos obtenidos en el análisis modal. Este proceso en sí, constituye la regresión aplicada en el árbol de decisión para determinar el subespacio de los modos analizados. De esta manera, se obtienen los parámetros del PSS para esta condición operativa. Sin embargo, al hacer uso de un proceso heurístico, es bien conocido que, se podría encontrar otro subespacio sub-óptimo que presente modos de oscilación muy cercanos. Así, para ejemplificar esta situación se presenta la matriz de confusión de la selección de los subespacios en la Tabla 3, los cuales fueron obtenidos para el sistema bajo análisis. Para este experimento, se consideró para cada subespacio una simulación de 520 diferentes puntos de operación, de los cuales existen 357 casos en los que no son adecuadamente clasificados. Este resultado representa una precisión de clasificación del 92,9 %. Los escenarios de clasificación errónea se deben principalmente a que, la condición operativa presenta modos de oscilación muy similares entre los subespacios involucrados.
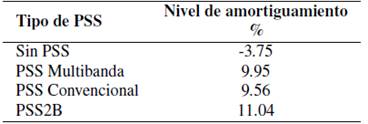
Por otro lado, en todos los subespacios, el sistema presenta un nivel de amortiguamiento positivo, lo que determina que, aunque exista la posibilidad de clasificación a un subespacio que no corresponda (este error se da principalmente entre los subespacios adyacentes) el sistema puede contar con un nivel adecuado de amortiguamiento. Para todos los modos de oscilación críticos el sistema alcanza un nivel de amortiguamiento superior o igual al 10 %, como se observa en la Tabla 4. Aquí, se detalla el nivel de amortiguamiento alcanzado por el sistema para cada uno de los tipos de PSSs. Note que, el de mayor nivel de amortiguamiento es obtenido con el PSS2B propuesto en este estudio, seguido del PSS Multibanda y PSS convencional.
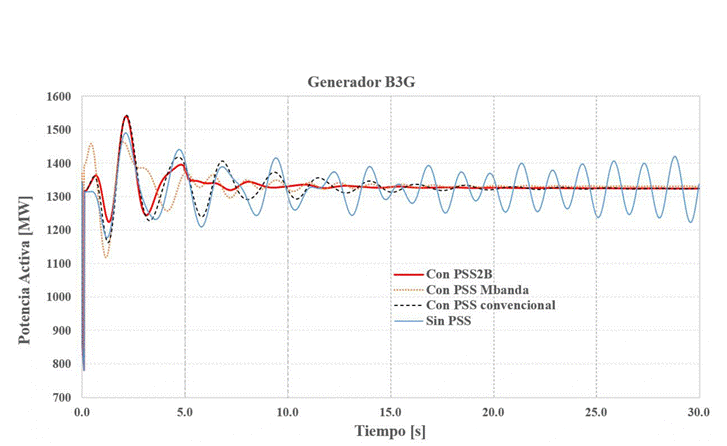
A continuación, se introduce la respuesta dinámica del sistema analizado, el cual es obtenido con la metodología propuesta. En la Figura , se presenta la respuesta dinámica derivada a partir del generador B 3G para los casos que contemplan el PSS1A (convencional), los PSS2B con el método propuesto y el PSS Multibanda. A partir de las curvas de esta figura, se puede observar que, cuando se consideran los PSS adecuadamente sintonizados el sistema cuenta con un nivel de amortiguamiento para las oscilaciones. Además, el enfoque de mejor respuesta es el PSS2B que considera los parámetros obtenidos por medio del árbol de decisión, gracias a una sintonización adaptativa seguido del PSS multibanda.
De acuerdo con la metodología utilizada, el conjunto de parámetros de sintonización del PSS2B puede ser modificado de forma adaptativa, considerando el punto de operación, en la búsqueda de mejorar el nivel de amortiguamiento del sistema. Cabe recalcar que, este tipo de técnicas no ha sido aplicado en virtud de que existe una solución ya ampliamente usada como son los PSS multibanda, como se mencionó a lo largo del documento. Sin embargo, esta alternativa puede ser atractiva en los casos en los que se cuenta con un PSS de menores prestaciones (como lo son PSS1A y PSS2B), mismos que se hallan operativos en una central. Al considerar la expansión del sistema, el mismo podría necesitar un PSS multibanda (p.ej., en el sistema eléctrico del Ecuador se ha determinado que esto efectivamente ha sucedido). Sin embargo, por restricciones presupuestarias no es factible el reemplazo por otra tecnología más sofisticada (el cambio tecnológico se ha estimado puede costar hasta 2 millones de dólares por unidad). Además, en el caso de Ecuador, al existir un sistema WAMS en operación comercial, la alternativa planteada en este trabajo podría ser una opción a considerar.
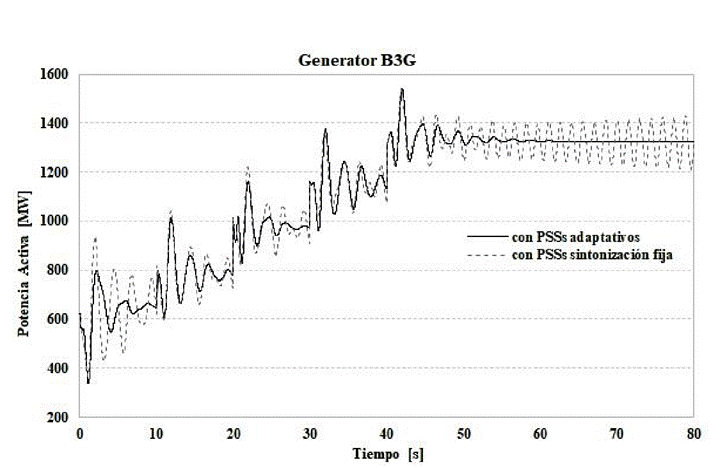
En la Figura , se muestra la respuesta dinámica ante incrementos sucesivos de carga, donde la curva punteada corresponde a la respuesta considerando la sintonización fija de los PSSs correspondiente al subespacio 5. Mientras que, la curva sólida denota la respuesta de la selección adaptativa del conjunto de PSSs de acuerdo con las condiciones operativas. En esta figura también se observa una mejor respuesta del nivel de amortiguamiento del sistema al considerar el método adaptativo ante las múltiples condiciones operativas.
CONCLUSIONES
En la actualidad, se mostró que es posible monitorear la dinámica del SEP mediante el uso de tecnología de medición fasorial, a través de registros obtenidos de PMUs como parte de un sistema WAMS. Esta disponibilidad permite plantear metodologías alternativas que conlleven a mejorar la estabilidad de pequeña señal del sistema, las cuales están siendo motivo de investigación. Esta premisa ha sido utilizada en este trabajo para definir una metodología de sintonización adaptativa de PSSs que usa las bondades de los árboles de decisión. Este nuevo enfoque ha permitido determinar el subespacio operativo en el cual se encuentra el sistema en tiempo real. De esta forma, fue posible seleccionar los parámetros óptimos de los PSSs definidos previamente en una etapa de sintonización fuera de línea que mejor se adapten a las condiciones operativas.
Aprovechando los diferentes tipos de PSSs existentes en un sistema de potencia, la propuesta presentada constituye una alternativa viable y económica, ya que se obtiene un similar amortiguamiento para los modos críticos existentes, que el que se obtuviese mediante un PSS Multibanda. Además, este enfoque demostró ser confiable sin la necesidad de incurrir en costos adicionales relacionados con la adquisición, instalación y sintonización de este equipo, factores que vuelven inviables este tipo de proyectos.
A través de la propuesta, se consiguió un apropiado nivel de amortiguamiento de los modos críticos, con un valor superior o igual al establecido como límite objetivo para todos los modos de oscilación. Estos resultados positivos justifican el estudio realizado y se constituyen en un punto inicial para continuar con el análisis de otros métodos de control de oscilaciones para aplicarlos a los sistemas de energía eléctrica.