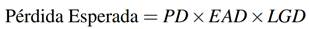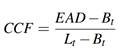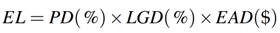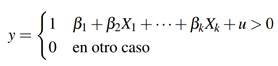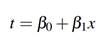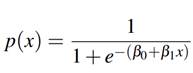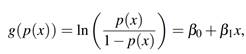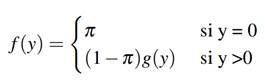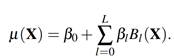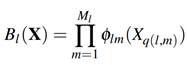Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
El negocio de intermediación financiera es una de las principales, sino la principal actividad de la industria bancaria, generadora de una parte importante de sus beneficios y como consecuencia generadora también de una parte importante de sus riesgos.
Este proceso de transformación de activos y pasivos o, en otras palabras, este proceso de intercambio (compra - venta) de riesgos en el que participan las entidades financieras está sujeto a una variedad de riesgos financieros y operativos. Uno de ellos el riesgo de crédito o de contraparte (counterparty risk), inherente a la gestión de carteras que tienen cuentas pendientes de cobro.
Si bien la palabra riesgo puede tener una connotación negativa, es posible usar una de sus tantas explicaciones etimológicas que a la vez nos sugiere la forma del cómo se debe abordarlo. () señalan que el vocablo riesgo proviene del latín risicare: atreverse o transitar por un sendero peligroso. Es en este sentido que las instituciones financieras deben abordar la gestión de riesgo de crédito, porque el negocio bancario supone precisamente esto: arriesgarse o atreverse a entregar dinero a un deudor sabiendo que existe el peligro de no pago, pero con el objetivo de administrarlo de tal forma que se pueda obtener una rentabilidad generadora
de valor para los dueños del capital o accionistas.
La teoría moderna del portafolio y por ende la actual administración del riesgo crediticio tiene como meta que su gestión permita buscar la rentabilidad que se adecúe al nivel de pérdidas esperadas que se esté dispuesto a asumir. Lo que se traduce en que un cliente con una mayor probabilidad de impago no se reduce a una negación sino a una correcta determinación del nivel de riesgo y por ende del precio (tasa de interés activa) para que se pueda obtener la rentabilidad esperada que compense el riesgo de crédito asumido. En este contexto, la medición de este tipo de riesgo se vuelve relevante, no sólo en su comprensión sino en su medición, desarrollando para esto varias metodologías de estimación de pérdidas.
Hace más de 20 años que el Banco JP Morgan publicó en su documento técnico Riskmetrics el concepto de Valor en Riesgo (VaR, por sus siglas en inglés), un modelo estadístico que permite medir cuantitativamente la pérdida máxima que puede experimentar una entidad financiera, con un nivel de confianza dado y en un horizonte temporal determinado (, ). Desde ahí hasta la actualidad, la medición del riesgo de crédito no ha tenido descanso en la búsqueda de mejoras permanentes de las técnicas empleadas en su estimación, porque el riesgo no se puede eliminar, pero sí se debe y puede administrar.
Una adecuada gestión permitirá optimizar el binomio rentabilidad-riesgo dado que existe una relación directa entre el nivel de riesgo que la entidad está dispuesta a asumir y el potencial de beneficios que se podrá generar (, ).
El resultado final del análisis de riesgo de crédito es poder obtener el nivel de pérdidas de capital que una entidad puede alcanzar producto del incumplimiento (default) de sus prestatarios. Este incumplimiento no es otra cosa que el deterioro progresivo observado en los activos de la institución y que se termina traduciendo en lo que hoy se conoce como pérdida esperada (PE).
La PE de una cartera de créditos indica el monto de capital que se podría perder en un horizonte dado, como resultado de la exposición al riesgo de incumplimiento de pago y representa el costo de hacer el negocio crediticio. Estas pérdidas deberían estar cubiertas por las reservas preventivas o provisiones (, ).
Pero, ¿es necesaria la medición y el control de riesgo de crédito en la vida real? La historia reciente nos responde que sí. En 2007, el mercado de créditos hipotecarios en EE.UU. dejó en evidencia la importancia de una adecuada administración y medición del riesgo. Las hipotecas subprime o hipotecas basura eran créditos otorgados a deudores con muy poca o ninguna liquidez ni solvencia para cubrir estas obligaciones y en donde las altas tasas de interés no compensaban el riesgo de crédito que se estaba asumiendo ( , ). El análisis post mortem de estas operaciones crediticias dejó en evidencia que los préstamos se daban a personas con trabajos precarios lo que incrementaba el riesgo de no pago. Pero, mientras el mercado hipotecario estaba al alza, se disfrazaba con su crecimiento el peligro asumido y latente. La única preocupación era lograr empaquetar la deuda en títulos que pudieran ser ofrecidos a inversores con un gran apetito por el riesgo y que buscaban altos retornos.
Se puede apreciar que la utilidad de la gestión y cuantificación del riesgo de crédito es evidente. Esta cuantificación, considerando los enfoques más avanzados entregados por el Comité de Supervisión Bancaria de Basilea, debe realizarse con base en los conceptos de frecuencia y severidad de las pérdidas. Las pérdidas por este riesgo se dividen en esperadas y no esperadas o inesperadas, las primeras relacionadas con los requerimientos de provisiones por incobrabilidad, mientras que las segundas se asocian con el requerimiento de capital regulatorio mínimo por riesgo crediticio.
Basilea propone a las instituciones financieras elegir entre dos métodos para la medición del riesgo de crédito:
Método Estándar: este enfoque plantea que los bancos realicen sus mediciones de riesgo de crédito empleando calificaciones o ratings provistos por externos, los cuales deben ser empresas calificadoras de riesgo con prestigio internacional. Para la estimación de los activos ponderados por riesgo de crédito, se aplicará a los saldos de cartera netos de provisiones específicas, un coeficiente de ponderación en función a esta calificación de riesgo.
Método Avanzado basado en ratings internos (IRB por sus siglas en inglés): este enfoque a diferencia del anterior incorpora nuevos términos para la cuantificación del riesgo crediticio. La estimación de pérdidas, basada en modelos internos, deberá calcular los componentes del riesgo de una determinada cartera u operación de crédito, los cuales son: a) la probabilidad de incumplimiento o default, b) la exposición en caso de incumplimiento y c) la pérdida dado el incumplimiento.
Este enfoque avanzado o de ratings internos propuesto por Basilea para la medición del riesgo de crédito se expone en el siguiente apartado.
Basilea y la estimación de pérdidas para la administración de Riesgo de Crédito
En su documento técnico de julio de 2005, An Explanatory Note on the Basel II IRB Risk Weight Functions, el Comité de Supervisión Bancaria de Basilea explica la pérdida tanto desde una perspectiva top-down, es decir desde una visión de portafolio, como desde una
bottom-up o desde sus componentes (, ).
Cuánto capital mantener es la clave de este ejercicio de estimación de pérdidas, pues las entidades financieras en su búsqueda de optimizar el binomio rentabilidad-riesgo tienen un incentivo para minimizar el capital que requieren porque al hacerlo se liberan recursos que pueden destinarse a inversiones rentables y aquí es cuando surge el trade-off entre riesgo y retorno, pues cuanto menos capital tienen las instituciones, mayor es la probabilidad de no ser capaces de responder a sus obligaciones porque las pérdidas experimentadas en un año fiscal no pueden ser cubiertas por la utilidad (beneficio) más el capital disponible, lo que puede conducir a una quiebra por insolvencia.
Basilea II propone, para determinar cuánto capital debe tener un banco en su enfoque IRB (Internal Rating Based), centrarse en la frecuencia de las insolvencias bancarias producto de las pérdidas crediticias que los supervisores bancarios están dispuestos a aceptar.
Mediante el uso de modelos estocásticos sobre un portafolio de créditos es posible estimar la máxima pérdida que se puede soportar con un nivel de confianza dado o en su defecto cuál sería ese nivel de pérdida que superará el capital de la entidad con una probabilidad pequeña y predefinida.
El número exacto de incumplimientos en un determinado año, el monto exacto adeudado al momento del incumplimiento o la tasa de pérdida real son variables aleatorias y las entidades bancarias no los pueden conocer de antemano, pero pueden estimar su promedio. El enfoque IRB de Basilea se fundamenta sobre estos tres parámetros de riesgo, los cuales se definen a continuación:
Probabilidad de incumplimiento (PI o PD) por grado de calificación que indica el porcentaje promedio de deudores que incumplirán en este grado de calificación en el transcurso del año. La probabilidad de incumplimiento es función de una ratio de riesgo, un intervalo de tiempo y del momento específico del tiempo en donde se evaluará el evento de default o incumplimiento.
Exposición en caso de incumplimiento (EAD) que proporciona una estimación del saldo pendiente de pago (montos recibidos más los posibles retiros que se puedan realizar a las líneas de crédito aprobadas) en caso de incumplimiento del prestatario. En otras palabras, su estimación debe considerar no sólo la deuda directa que mantiene el deudor, sino la exposición potencial de las operaciones contingentes que pueden volverse cartera en el futuro.
Pérdida en caso de incumplimiento (LGD) que es el porcentaje de exposición que el banco podría perder en caso de incumplimiento del prestatario. La pérdida en caso de incumplimiento o severidad busca medir la pérdida que sufriría el acreedor después de haber realizado todas las gestiones posibles para lograr recuperar los créditos impagos.
Con estos tres factores, la pérdida esperada en montos monetarios se puede escribir como:
Saldo expuesto al default en el contexto de Basilea y su tratamiento para un portafolio de tarjetas de crédito
La exposición o el saldo expuesto al incumplimiento o al default no es otra cosa que el importe de la deuda que está pendiente de pago al momento en que el prestatario cae en incumplimiento.
Por lo general, al momento del incumplimiento, suele ocurrir que la exposición coincide con el saldo impago de la operación crediticia, pero esto no es una regla absoluta. En productos con límites explícitos como las tarjetas de crédito, hay una proporción de este límite que no está en uso hoy, pero que puede usarse durante el tiempo que el deudor tarda en caer en default. Por tanto, el cálculo de la exposición debe incorporar no solo la parte del límite o cupo de la tarjeta de crédito que se está usando, sino también el potencial incremento de saldo que pudiera generarse desde una fecha de referencia hasta el momento en que se declare impago.
Como consecuencia de esto, la EAD se obtiene como la suma del riesgo asumido de la operación más un porcentaje del riesgo no dispuesto respecto del límite disponible por el cliente. EAD =Saldo utilizado del límite o cupo disponible + Porcentaje del saldo no utilizado del límite o cupo disponible al momento del incumplimiento.
Este porcentaje se calcula a partir del Credit Conversión Factor (CCF) y en la literatura es común que la estimación de la EAD se reduzca a encontrar este Factor de Conversión. Se puede definir al CCF como el porcentaje sobre el saldo no dispuesto o no utilizado que se espera vaya a emplearse antes o hasta que se produzca el incumplimiento (, ).
Para la estimación de la EAD en el caso de las tarjetas de crédito, objeto de este estudio, Basilea II y III sugieren el uso de datos históricos que permitan evaluar el CCF, de tal forma que a partir del comportamiento reciente de los clientes se pueda, aunque
parcialmente, conocer cuál será el saldo expuesto al default.
Si bien el acuerdo de Basilea no define como mandatorio el cálculo del CCF para estimar la exposición al incumplimiento, es una referencia recurrente a lo largo de la documentación generada por el Comité, esta aproximación hace que la precisión en la estimación de la EAD recaiga sobre la calidad de los modelos para el CCF.
No obstante, los modelos para estimar el Credit Conversion Factor han enfrentado importantes retos estadísticos dado que la distribución de esta variable no se ajusta a las distribuciones estadísticas estándar. Según (), las distribuciones del CCF tienden a ser bimodales con una función de probabilidad en cero y otra en uno, entre ambas una distribución relativamente plana (ver Figura ).
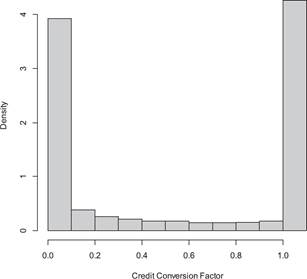
Figura 1 Característica de la distribución del Credit Conversion Factor después de haber realizado un truncamiento de la función (, )
() definen el cálculo del Credit Conversion Factor como:
Siendo B t el saldo empleado, L t el límite de la línea de crédito y suponiendo que, en el tiempo t antes del default (t d ), una operación de crédito puede caer al incumplimiento en el periodo t d > t con un saldo B t d = EAD.
Esta expresión nos deja ver dos deficiencias substanciales: la primera es una singularidad inherente que indefine al estimador para cuentas (líneas de crédito) totalmente desembolsadas y numéricamente inestable para aquellas que han sido usadas casi en su totalidad. El segundo problema es que el CCF puede exceder en valores al rango [0,1]proporcionando estimaciones de la EAD que carecerían de intuición económica, situación que en la práctica se ha encontrado con frecuencia (, ). En palabras de (), el CCF no es un modelo universalmente apropiado para la estimación de la EAD, proveyendo predicciones que son poco sensibles desde el punto de vista del negocio y son también inconsistentes con la evidencia empírica.
() proponen mantener el cálculo del CCF, definido como una función del EAD, e indican las condiciones a cumplirse para poder utilizarlo. No obstante, así planteado, el EAD sigue siendo un cálculo imprescindible para implementar su propuesta. Dado que LGD también se presenta como una distribución bimodal, trabajos como () se enfocan en su estimación, y sostienen que su propuesta también puede ser usada para la estimación de la EAD.
() proponen la estimación de la pérdida esperada (EL) mediante un modelo de riesgo crediticio de dos etapas que integra: (1) aprendizaje de conjunto (ensamble learning) de clases no balanceadas para predecir PD y (2) una predicción de EAD utilizando un ensamble de regresión.
Como se ha indicado previamente, la literatura y aplicaciones comunes realizan la estimación de la EAD como función de CCF, pero esta última es altamente bimodal y puede sesgar la estimación de EAD. Trabajos recientes como () y
() proponen estimar la EAD directamente, sin CCF. El presente trabajo también estima directamente la exposición al default
y se ignora el habitual cálculo del CCF.
Para lograr esto, dado que la cantidad de saldo expuesto mayor a cero tiene una distribución sesgada a la derecha, la EAD se modeliza como una variable de respuesta continua, empleando un modelo de regresión lineal generalizado usando la distribución Gamma (, ). Además, se usa un modelo Regresión Spline Adaptativa Multivariante como método alternativo el enfoque tradicional paramétrico de estimación. Posterior a esto, la probabilidad de ocurrencia de una EAD con valor igual a cero se estudiará con un modelo logístico.
Finalmente, el desempeño de estos modelos es contrastado contra el saldo expuesto observado al momento del default del grupo de prueba y también contra el saldo expuesto observado de un grupo distinto de clientes en un periodo diferente al empleado para el grupo de construcción y prueba del modelo. Este trabajo utiliza un conjunto de datos reales de una entidad financiera ecuatoriana que tiene un portafolio de tarjetas de crédito.
METODOLOGÍA
Tanto desde la perspectiva de la gestión del riesgo como desde el punto de vista regulatorio, la estimación del riesgo de crédito es de gran relevancia. Este se basa en el análisis de las pérdidas esperadas (EL):
donde la probabilidad de incumplimiento (PD), la severidad (LGD) y la exposición del activo (EAD) juegan un papel fundamental.
En particular, Basilea II y III recomiendan que para la estimación de la exposición se use la proporción de la cantidad actual no utilizada que probablemente se utilizará en el momento del incumplimiento, o factor de conversión del crédito (, ). No obstante, esta recomendación no es vinculante y trabajos como (), (), () y () han mostrado que la estimación directa de la exposición puede ser realizada sin necesidad de la utilización del factor de conversión.
Por ejemplo, () proponen un modelo para la estimación directa de la EAD usando tres variables de resultado:
El saldo pendiente de pago por parte del deudor al momento del default, entendido este como el saldo actual al incumplimiento más los intereses contabilizados a la fecha.
El límite de la línea de crédito a la fecha del default y
La fecha de incumplimiento
La estimación de los parámetros del modelo requiere la construcción de tres componentes: a) una regresión logística para predecir la probabilidad de una reducción en el límite de la línea de crédito; b) un modelo de mezclas finitas con dos densidades normales para predecir la EAD (transformada a escala logarítmica en base 10), dada una disminución del límite; y c) una regresión por mínimos cuadrados ordinarios (MCO) para predecir el EAD transformado, sin una disminución del límite de la línea de crédito.
En este contexto, la estrategia de modelización del presente trabajo consiste en dos etapas que luego son combinadas para obtener una estimación final.
Cuando EAD=0, usa el modelo logit para la estimación. Después, si EAD>0, de un grupo de distribuciones candidatas se determina la distribución de probabilidad que más se ajusta al EAD observado. La elección de la distribución se basa en estadísticos de bondad de ajuste como Kolmogorov-Smirnov, Cramer-von Mises and Anderson-Darling (, ). Finalmente, una vez elegida la distribución de la variable respuesta, la estimación se realiza mediante un modelo lineal generalizado (GLM por sus siglas en inglés).
Además de la estimación del GLM para modelizar la EAD, este trabajo evalúa empíricamente métodos estadísticos alternativos y realiza un benchmark de los resultados obtenidos, específicamente, el modelo MARS. Trabajos como () han usado exitosamente técnicas de ML en el contexto de riesgo de crédito.
Datos
Este trabajo presenta un esquema de modelización basado en datos de entrenamiento, prueba y validación. Este es un esquema que se usa ampliamente en la modelización de aprendizaje automático y ciencia de datos (, ).
El conjunto de datos consiste en más de 200 mil observaciones de tarjeta habientes de un banco ecuatoriano. Los trabajos de () y de () se han basado en 2.144 y 10.271 observaciones, respectivamente. Este volumen de información ha permitido sin restricciones poder dividir la información de las cuentas en periodos. Se ha trabajado sobre dos periodos de observación, el primero es desde diciembre de 2017 hasta noviembre de 2018 con un total de 212.796 registros. Este grupo de cuentas sirve para la construcción del modelo y para obtener el grupo de prueba contra el cual se contrasta el resultado del modelo con la EAD observada.
El segundo periodo de observación se comprende desde diciembre de 2018 hasta noviembre de 2019 con 221.213 tarjeta habientes y es empleado únicamente para contrastar la precisión del modelo obtenido para el cálculo de la EAD con un grupo de clientes en un periodo distinto al de la población de construcción y prueba.
Junto con la muestra de clientes se obtienen o calculan variables explicativas que son empleadas en los modelos que se usan para la estimación de la EAD y su posterior validación. Este conjunto de variables se puede obtener tanto al momento del default (t d ) como a la fecha de referencia o de corte de la información (t r ), en este caso esta fecha es diciembre de 2017.
La siguiente lista muestra las variables que se consideran en los modelos para la estimación de la EAD:
Límite o Cupo de la TC o Tarjeta de crédito - L(t r ): Cupo asignado a la tarjeta a la fecha de corte.
Cupo utilizado - E(t r ): Cupo utilizado a la fecha de corte.
Cupo no utilizado - L(t r ) − E(t r ): Cupo de la tarjeta menos el cupo utilizado a la fecha de corte.
Porcentaje de uso de la TC - E(t r )/L(t r ): Cupo utilizado a la fecha de corte dividido para el cupo asignado a la tarjeta a la fecha de corte.
Tiempo al default - t d − t r : Fecha de caída al incumplimiento menos la fecha de corte.
Segmento de riesgo - R(t r ): Clasificación de riesgo medida por el score de comportamiento, a la fecha de corte.
Promedio de días de atraso: Número promedio de días de no pago, medidos a los 3, 6, 9 y 12 meses anteriores a la fecha de corte.
Porcentaje de cupo no usado de la TC - (L(t r ) E(t r ))/L(t r ): Porcentaje de cupo no usado a la fecha de corte dividido para el cupo o límite de la tarjeta a la fecha de corte.
Cupo utilizado al default - E(t d ): Cupo utilizado al momento del default o incumplimiento.
Límite o Cupo de la Tarjeta de crédito (TC) al default - L(t d ): Cupo o límite de la tarjeta de crédito al momento del incumplimiento.
Incremento de cupo: Variable binaria que indica 1 si tuvo un incremento de cupo durante los 12 meses anteriores a la fecha de corte o 0 en caso contrario.
Cambio absoluto en el cupo utilizado: Cambio en valor en el cupo utilizado calculado como la diferencia entre el Cupo utilizado a la fecha de corte menos el cupo utilizado 3, 6, 9 y 12 meses antes de la fecha de corte.
Cambio relativo en el cupo utilizado: Cambio relativo en el cupo utilizado calculado como la diferencia entre el Cupo utilizado a la fecha de corte menos el cupo utilizado 3, 6, 9 y 12 meses antes de la fecha de corte dividido para el cupo utilizado a la fecha de corte.
Segmento RFM: Clasificación de RFM (recencia, frecuencia y monto) a la fecha de corte.
La literatura alrededor de este tema en específico o en trabajos enfocados a calcular la probabilidad de default han trabajado con varios sets de variables como la calificación de riesgo del prestamista, el número de créditos otorgados, el límite de la línea de crédito, saldo, plazo, antigüedad del cliente, garantías, edad, género, ingreso, tipo de relación laboral, número de transacciones, valor de las transacciones, estado civil, lugar de nacimiento o lugar de residencia, cupo o límite utilizado, cupo o límite disponible, categoría de riesgo, atraso promedio, si ha tenido incremento de cupo o límite (, ; , ; , ).
Nuestro artículo incorpora varias de estas variables trabajadas en la literatura y adiciona una en específico que recoge tres características que se relacionan directamente con el uso del saldo en el caso de las tarjetas de crédito. Esta variable es el segmento RFM, la cual categoriza a los clientes de la entidad financiera, tenedores de tarjeta de crédito en torno al comportamiento en la recencia (R) o el tiempo transcurrido desde la última compra; la frecuencia de uso (F), es decir, el número de veces que ha comprado en el pasado y el valor monetario (M) o la cantidad de dinero gastada en total por el cliente con la línea de crédito.
Si bien esta variable RFMtiene como finalidad identificar los mejores clientes para incrementar la venta, en este estudio queremos evaluar su incidencia en el uso del límite de la línea de crédito y, por tanto, el incremento en la exposición al momento del default. Los resultados intuitivos sugieren que un alto valor del RFM (cercanía en la compra, mayor transaccionalidad y valor monetario) debería corresponderse con un mayor uso de la línea o cupo de la tarjeta, comprometiendo un mayor monto al momento del incumplimiento.
Modelo Logit
Uno de los principales motivos de la amplia utilización del modelo logit es el hecho de que puede estimar modelos cuando la variable dependiente es binaria, es decir, toma valores cero o uno. Esta característica hace que el modelo de regresión lineal múltiple clásico no sea viable en este tipo de variables dependientes debido a que sus predicciones pueden tener valores negativos, así como valores superiores a uno.
Formalmente, la regresión logística o logit puede formularse como:
Suponga un modelo con una variable explicativa x, entonces
Ahora la función logística
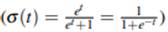se puede expresar como:
Donde p(x) representa la probabilidad de que y = 1.
El modelo logit pertenece a la familia de los modelos lineales generalizados. Para observar este particular se define la inversa de la función logística:
Lo que indica que esta función define un modelo lineal a partir de la función logística de enlace.
Modelo Gamma
Sea y i la EAD observada para el i-ésimo cliente, i = 1, ..., n (por simplicidad se omite el índice i en adelante); x denota la matriz de covariables observados para cada cliente. La función de densidad para y es mixta:
donde g(y) es la función de densidad de una distribución continua y π es la probabilidad de la EAD en cero, en este caso se usa un modelo lineal generalizado para variable dependiente con distribución Gamma.
Mars
MARS, o Regresión Spline Adaptativa Multivariante (Multivariate adaptive regression spline) es una forma de regresión introducida por Jerome Friedman (, ). MARS es una técnica de regresión no paramétrica y puede ser vista como una extensión de los modelos lineales que automáticamente identifica no linealidades e interacciones entre variables. El término MARS está protegido por derechos de autor y pertenece a Salford Systems. Para evitar violentar esos derechos, las implementaciones abiertas de MARS se suelen llamar Earth (El paquete earth en R (, )).
2RFM model o modelo RFM es una técnica que busca segmentar clientes en función de tres atributos: Recencia, Frecuencia y Valor Monetario, con el objetivo principal de incrementar los ingresos de la empresa. Esta medida nos permite incorporar en un solo indicador la importancia de la transaccionalidad del cliente tanto en número como en valor monetario
3Los resultados del modelo confirman la intuición. (ver Tabla 1 variable Rfm)
En este modelo (, ), Y = µ (X) + ε donde X es la matriz de covariables y ε es el término de error con media cero. La función de regresión µ (X) es la suma ponderada de L funciones base:
Cada función base (l):
es el producto de M
l
funciones spline univariantes
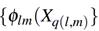donde M
l
es un número finito y q(l, m) es un índice que depende de la función base (l) y la función spline (m).
MARS es ideal para usuarios que prefieren obtener resultados similares a la regresión tradicional mientras capturan no linealidades e interacciones necesarias. Revela patrones importantes en los datos que otras técnicas suelen fallar en revelar. También construye su modelo uniendo pedazos de líneas rectas que mantienen su propia pendiente. Esto permite que se detecte cualquier patrón en los datos. Se puede utilizar para cuando se tiene variables de respuesta cuantitativa y cualitativa. MARS realiza, automáticamente y con gran velocidad: selección de variables, transformación de variables, detección de interacciones, testeo. Para detalles formales del modelo ver ().
RESULTADOS
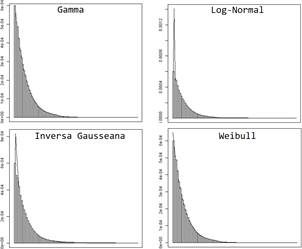
La Figura muestra el ajuste de diferentes distribuciones de probabilidad para la exposición. Se puede apreciar que se tiene una variable con una fuerte asimetría positiva. Esta característica de la distribución descarta opciones de modelización más tradicionales como cuando se asume normalidad en la variable de respuesta, ampliamente estudiadas en textos de econometría clásica (, ).
Una de las tareas centrales en el análisis de datos paramétrico responde a la elección del modelo que mejor se ajusta a los datos analizados (, ). Usando el paquete (), las distribuciones de probabilidad candidatas para el ajuste de la exposición fueron: Gamma, Inversa Gausseana, Log-normal y Weibull y se muestran en la Figura . La Figura muestra el histograma de la variable analizada (EAD), así como las densidades estimadas para cada una de las candidatas. Se usa el criterio de Kolmogorov-Smirnov para evaluar la bondad de ajuste de donde se obtuvieron, respectivamente: 0.00533, 0.37897, 0.07263 y 0.00716. Este criterio indica que el mejor ajuste es el de la distribución Gamma.
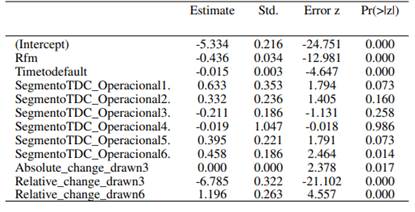
Una vez identificada la distribución de probabilidad de la variable dependiente, se procede a la estrategia de modelización basado en dos etapas. La primera etapa consiste en estimar un modelo para valores de exposición igual a cero. Para este objetivo se usa un modelo logit. La segunda etapa consiste en la modelización de la exposición para valores mayores a cero usando la distribución gamma como supuesto distribucional de la variable dependiente y el modelo MARS. Los resultados del modelo logit se muestran en la Tabla .
El modelo elegido (ver Tabla ) tiene un total de 6 variables, todas ellas son significativas a un nivel del 5 %. La variable SegmentoTDC tiene 7 niveles que en conjunto, usando el test de Wald, son significativos al 5 %. Respecto a los niveles, de manera individual, el nivel 6 es significativo al 5 %, los niveles 1, 5 y 6 son significativos al 10 % y los niveles restantes no son significativos a estos niveles de significancia.
Este modelo nos permite identificar a los clientes cuya predicción de exposición sea igual a cero. Es decir, ante un nuevo conjunto de información, el primer modelo en estimarse es el logit. Los clientes que tengan una probabilidad mayor al umbral estimado se consideran con predicción igual a cero.
El umbral elegido para determinar la probabilidad de que la exposición sea igual a cero se realiza mediante la estimación de la curva ROC (Receiver Operating Characteristic) que indica el balance que existe entre la especificidad y la sensibilidad para cada punto de corte. Se elige el punto más cercano al par ordenado (0,1) porque estos valores indican una mejor clasificación. Cabe indicar que el área bajo la curva de este modelo es 94 %, que es mejor mientras más cerca de 100 % se encuentre. En los datos de prueba del modelo logit se obtiene una sensibilidad del 88 % y una especificidad de 93 %.
En la segunda fase de modelización, se estima un modelo de regresión basado en modelos lineales generalizados cuyos resultados se muestran en la Tabla del Anexo A. Se puede apreciar que todas las variables de este modelo son significativas. Asimismo, la Tabla del Anexo B muestra los coeficientes ajustados del modelo MARS.
La estimación comparada con lo observado en los datos de prueba del modelo gamma y MARS se presenta en la Figura . Se puede apreciar que la predicción tiene una distribución similar a la observada en ambos casos.
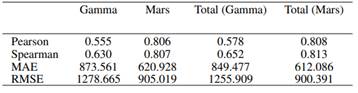
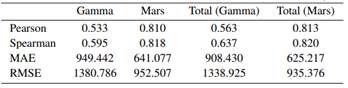
Las Tablas y muestran cuatro medidas de rendimiento usadas para evaluar modelos cuya variable dependiente es cuantitativa (, ). La correlación de Pearson y la correlación de Spearman indican mejores rendimientos cuanto más alta es. El MAE y la raíz del MSE son mejores cuanto más bajo es su valor. Como es de esperarse, se puede apreciar que las medidas de rendimiento del modelo presentan rendimientos más bajos en la medida en que se trabaja con valores no observados. Por ejemplo, la correlación de Spearman tiene un valor inicial de 0.630 en la fase de prueba del periodo 1 (Tabla ). Pero en el periodo 2 (Tabla ) es de 0.595, muestra una ligera disminución.
Es notorio que el uso del Modelo MARS supera considerablemente al modelo Gamma. Debe también destacarse que el modelo combinado (columnas Total de las tablas y ) muestra mejores valores de rendimiento que únicamente los modelos parciales que no toman en cuenta EAD = 0. Esto indica que el uso del modelo logit para predecir la exposición igual a cero aporta al rendimiento de las predicciones.
3.1 Discusión
De la literatura revisada, (), (), () y () son los trabajos que más se alinean con la presente investigación debido a que los tres no requieren de la estimación del factor de conversión (CCF) para estimar la EAD. No obstante, () se aleja de nuestro objetivo ya que su propuesta está dirigida a la estimación de la pérdida esperada (PD).
(), () y nuestro aporte estiman directamente la EAD de un portafolio de líneas de crédito. El primero lo hace en un banco del Reino Unido con datos mensuales desde enero 2001 a diciembre 2004, el segundo estima la EAD en un Banco de Asia con datos mensuales entre enero del 2002 y mayo 2007, mientras este trabajo lo hace en un banco ecuatoriano con datos mensuales desde diciembre 2017 a noviembre 2019. Un hallazgo común en las tres investigaciones es concluir que la EAD observada sigue una distribución gamma. Esta conclusión es importante porque es obtenida a partir de fenómenos que se observan en diferentes latitudes y horizontes de tiempo, sugiriendo que esta sería la distribución natural de la EAD.
La estrategia de modelización que sigue el presente trabajo es diferente de la de () y (). Por un lado, sus propuestas estiman simultáneamente los parámetros para EAD=0 y EAD>0 mediante el modelo GMLSS (Generalized additive model for location, scale and shape). Por otro lado, nuestro aporte separa las estimaciones en dos etapas que luego son combinadas. La correlación de Pearson en () es 0 .798, en () es 0.937 y en nuestro trabajo es 0.813. Esto muestra que, como lo hacemos en nuestro aporte, la estrategia de modelización para la estimación de la EAD puede ser abordada de manera separada manteniendo resultados competitivos con los obtenidos en otros trabajos.
CONCLUSIONES
En los modelos de estimación de pérdidas por riesgo de crédito minorista (retail credit risk), la estimación de la probabilidad de default ha sido permanentemente el principal foco de investigación y la literatura es extensa no sólo en los documentos científicos sino también en los libros académicos que abordan este componente de la pérdida esperada. En cambio, la Exposición al Default (EAD) o Saldo Expuesto al Incumplimiento tanto en la industria financiera como en la literatura académica ha sido una de las áreas más débiles de medición y modelización por lo que este trabajo representa un aporte en el esfuerzo de medición del EAD.
La correcta medición de la EAD en un portafolio de tarjetas de crédito permite a la institución financiera reducir el riesgo de subestimación de pérdidas esperadas e inesperadas y por tanto tener un mejor control en la optimización de la evaluación del desempeño de la cartera, el rendimiento sobre el capital ajustado por riesgo, las decisiones relativas a la operación, el análisis de rentabilidad, así como a la toma de decisiones respecto a la estructura de capital.
En líneas de crédito como es el caso de la tarjeta, en donde hay una porción del límite o cupo de la línea que aún no se ha usado, la estimación de la EAD demanda considerar el porcentaje del saldo no utilizado al momento del incumplimiento. Para esto, calcular el CCF ha sido la regla general en la mayoría de las estimaciones realizadas. No obstante, estos modelos han enfrentado importantes retos
estadísticos dado que la distribución de esta variable no se ajusta a las distribuciones estadísticas estándar, tienden a ser bimodales con una función de probabilidad en cero, otra en uno y una distribución relativamente plana entre ambas.
Sumado a lo anterior y siguiendo a (), existen dos deficiencias en el uso del CCF: la primera es una singularidad inherente que indefine al estimador para cuentas (líneas de crédito) totalmente desembolsadas y numéricamente inestable para aquellas que han sido usadas casi en su totalidad. El segundo problema es que el CCF puede exceder en valores al rango [0,1] proporcionando estimaciones de la EAD que carecerían de intuición económica. El presente trabajo emplea un modelo que omite el CCF como mecanismo de estimación de la EAD, eliminando las deficiencias asociadas al mismo y obteniendo buenas estimaciones.
Se ha mostrado a lo largo del trabajo que el primer desafío es la identificación de la distribución de probabilidad de la variable dependiente. Para lograr este objetivo se plantearon diferentes distribuciones candidatas y se evaluó la bondad de ajuste entre la variable observada y la distribución teórica propuesta.
Se ha demostrado que es posible la estimación de la EAD omitiendo el cálculo del Factor de Conversión de Crédito. Para este objetivo se ha empleado una regresión con modelos lineales generalizados dada una distribución Gamma en la variable dependiente y el Modelo MARS, resultando este último muy superior al primero.
Los resultados empíricos obtenidos con datos de entrenamiento han sido validados con dos muestras distintas, unos datos de prueba sobre el mismo periodo de la información de entrenamiento y unos datos de validación que corresponden a un periodo de tiempo diferente a los de entrenamiento y prueba, encontrando resultados estables en ambos casos, lo que significa que se puede implementar un modelo para la estimación de la EAD combinando los resultados obtenidos para cuando EAD = 0 y EAD>0.
Como se ha indicado en la sección de discusión, los resultados obtenidos son competitivos con los que se encuentran en la literatura. Esto muestra que la estimación simultánea de parámetros, así como la estimación separada (EAD = 0 y EAD>0) arrojan resultados prometedores y a la vez dejan la puerta abierta a futuras investigaciones para aquellos investigadores interesados en llegar a un consenso en cuanto a estrategia de modelización.
Otro elemento que puede ser de interés en futuras investigaciones es la identificación e incorporación de un conjunto mínimo de covariables que deban incluirse en los modelos independientemente de la estrategia de modelización. Las covariables que hemos usado responden a investigaciones previas y a nuestra experiencia en el sector. Sin embargo, de nuestra revisión de literatura, la identificación de determinantes de la EAD sigue siendo una pregunta abierta y al momento la elección de variables se ha realizado tanto a través de criterio experto como estadístico.
Este trabajo puede ser un insumo importante para la estimación más fina de las pérdidas en la cartera de clientes de tarjeta de crédito en Ecuador y puede ser utilizado por la institución de tal manera que permita cumplir con la normativa vigente, así como tener resultados más precisos desde el punto de vista estadístico.
