1. INTRODUCCIÓN
La fibra óptica es uno de los medios de transmisión más utilizados en la actualidad en sistemas de telecomunicaciones de gran capacidad, gracias a ventajas como su gran ancho de banda, alta inmunidad al ruido y a la interferencia electromagnética, baja atenuación, entre otras, que hacen de la fibra el medio ideal para satisfacer necesidades de conectividad, velocidad y disponibilidad en cualquier sistema de telecomunicaciones.
Dada la creciente demanda que experimentan hoy en día los servicios de telecomunicaciones, los sistemas deben soportar cada vez más volúmenes de información con un desempeño óptimo, que implica elevadas tasas de transmisión, lo que a su vez provoca la aparición de ciertos fenómenos que alteran las señales ópticas transmitidas, los cuales no son de consideración a bajas velocidades. Uno de estos fenómenos, es la dispersión por modo de polarización (Polarization Mode Dispersion, PMD).
La PMD es otro tipo de dispersión presente en una fibra óptica que degrada a los pulsos ópticos que se propagan por ella, ocasionando un ensanchamiento temporal de los mismos. La PMD es causada por la birrefringencia de la fibra óptica, la cual provoca que cada uno de los dos estados de polarización (Principal States of Polarization, PSP) de un modo viajen a distinta velocidad de propagación, dado los diferentes valores de índice de refracción que cada componente ve, y por lo tanto, que ambos estados lleguen al otro extremo de la fibra en tiempos distintos (Martín Pereda, 2004). La diferencia entre los retardos de cada estado de polarización se denomina retardo diferencial de grupo (Differencial Group Delay, DGD) y es el parámetro que determina la magnitud de la PMD que tendrá la fibra (Leiva et al., 2007). La PMD a su vez puede causar interferencia entre símbolos (Inter-Simbol Interference, ISI) y consecuentemente incrementar la tasa de bits errados del sistema.
Las fibras ITU-T G.655 usadas en este trabajo, son fibras monomodo de dispersión desplazada no nula (Non Zero Dispersion Shifted Fiber, NZDSF); es decir, fibras cuyo perfil de índice de refracción ha sido modificado de tal manera que el punto de mínima dispersión cromática se encuentra a una longitud de onda alrededor de los 1,55 µm (tercera ventana), para de esta forma, combatir los fenómenos no lineales presentes en las fibras monomodo estándar, esencialmente el de mezcla de cuatro ondas (Four Wave Mixing, FWM) (Hetch, 1999).
En la sección 2: “Análisis Matemático de la PMD”, se analiza el fenómeno de PMD, sus causas y efectos, por medio de expresiones matemáticas utilizadas en anteriores investigaciones con excelentes resultados. Además, se describe una técnica de post-compensación de la PMD basada en el uso de polarizadores y splitters ópticos en el lado del receptor. En la sección 3: “Simulación de PMD”, se muestran los resultados de la simulación PMD y su compensación, en diferentes escenarios, variando los parámetros de distancia, velocidad de transmisión y coeficiente PMD. Para las simulaciones, se usa el software computacional OptiSystem 14.2, pues presta las facilidades requeridas para los propósitos de este trabajo de investigación.
2. ANÁLISIS MATEMÁTICO DE LA PMD
2.1 Birrefringencia de la Fibra Óptica
El origen físico de la PMD es la birrefringencia de la fibra óptica que se produce por “la diferencia entre los índices de refracción de los ejes ortogonales de la fibra llamados también ejes de birrefringencia (Rodirguez Barrios, 2007)” y que puede ser determinada mediante la Ecuación (1).
Donde
El hecho de que cada eje ortogonal presente distintos índices de refracción se debe a la geometría imperfecta del núcleo de la fibra, producida bien sea durante su proceso de fabricación, por esfuerzos aplicados o por diferencias de temperatura a las que se somete la fibra. Por lo tanto, la geometría del núcleo de la fibra no es un círculo perfecto sino que adquiere una forma elíptica.
Consecuencia de aquello, cuando un pulso de luz viaja por una fibra monomodo, el modo fundamental de propagación se divide en sus dos estados de polarización ortogonales independientes entre sí, correspondientes a los ejes (x, y) de su campo eléctrico.
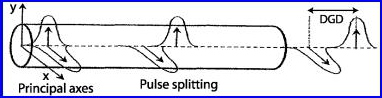
Figura 1. Propagación de los dos estados de polarización de un pulso de luz a través de un segmento de fibra birrefringente.
La energía de dicho modo se reparte entre ambos estados de polarización y como cada estado “ve” un índice de refracción diferente, se propagará a distinta velocidad a través de la fibra y llegará al otro extremo de la misma en diferente tiempo (Rojas et al., 2004), como se observa en la Figura 1 (Agrawal G. P., 2006).
Cuando se tienen segmentos de fibra monomodo muy cortos, tanto el valor de birrefringencia como la orientación de sus ejes ortogonales son fijos. Sin embargo, en fibras de gran longitud como las utilizadas en enlaces metropolitanos, nacionales, regionales o intercontinentales, la magnitud de la birrefringencia y la orientación de los ejes ortogonales, experimentan cambios y rotaciones aleatorias a través de su longitud y en el tiempo, lo cual ocasiona intercambios y redistribuciones de energía entre los PSP del pulso de luz que se propaga a través de dicha fibra.
A fibras monomodo de gran longitud se las puede modelar como la concatenación de varios segmentos pequeños de fibra de birrefringencia constante, cuya magnitud y dirección de sus ejes cambia aleatoriamente, como se muestra en la Figura 2 (Leiva et al., 2007). A esta concatenación se llama “Acoplamiento de Modos Aleatorio” en la que los PSP del pulso que se propaga viajan adelantándose y retrasándose entre sí (Photonics, 2012) (Leiva et al., 2007).
2.2 Coeficiente PMD
El Retardo Diferencial de Grupo (Diferential Group Delay, DGD), “
En segmentos de fibra cortos, el DGD viene dado por la diferencia en los tiempos de llegada de cada PSP del pulso, luego de recorrer una distancia “L”. Según (Agrawal, 2006) la expresión matemática del DGD corresponde a la Ecuación (2).
Donde
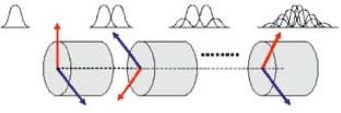
Figura 2. Concatenación de varios segmentos de fibra birrefringentes. El pulso que se propaga a través de esta fibra, sufrirá diversos niveles de dispersión aleatorios.
Se define como Coeficiente PMD “
Es decir:
En segmentos de fibra de gran longitud, como consecuencia del acoplamiento de modos aleatorio, se presenta un DGD de naturaleza estocástica, que obedece a una curva de distribución de Maxwell, cuya PDF se presenta en la Ecuación (5) según (Leiva et al., 2007).
Como se observa, dicha distribución es controlada solamente por el parámetro DGD promedio “
Según (Agrawal G. P., 2006) y (Ondrej, 2010), el coeficiente PMD en este tipo de fibras no es una función inversa de la longitud de la fibra “L”, sino de la raíz cuadrada de dicha longitud y sus unidades son los (
El DGD en términos del ancho de los pulsos de entrada y salida se expresa como la raíz cuadrada de la diferencia de ambos, de acuerdo a la Ecuación (7) (Elbers et al., 1991).
Donde τ y
Siendo P(t) la potencia del pulso medida en (W).
La recomendación ITU-T G.663 indica que el DGD máximo para un segmento de fibra debe ser menor al 30% del tiempo de bit “
En la práctica, normalmente se establece un valor de DGD igual a la décima parte del tiempo de bit para evitar dicha penalidad y una degradación importante de los pulsos ópticos transmitidos.
2.3 PMD en el sistema de Jones
El Algebra de Jones es un conjunto de vectores y matrices usados para describir la propagación de pulsos de luz a través de medios ópticos lineales, como es el caso de la fibra óptica.
De acuerdo a esto, un pulso de luz puede ser descrito en base a las componentes en los ejes (x, y) de su vector campo eléctrico, de acuerdo a la Ecuación (9) (Rodríguez Barrios, 2007).
Donde E, es el vector de Jones asociado al pulso de luz a propagarse.
El álgebra de Jones también permite modelar el comportamiento y las propiedades de un segmento de fibra birrefringente. El modelo Waveplate o Lámina de Onda ha sido utilizado para describir las propiedades ópticas de una fibra birrefringente con excelentes resultados (Elbers et al., 1991).
En este modelo se considera una rotación y desfase aleatorio de los estados de polarización de la luz que viaja por el medio. El propósito del retardador de fase es introducir una diferencia en los tiempos de llegada de cada componente ortogonal de polarización de la señal y un cambio en la fase de dichas componentes. El rotador de fase se usa para generar una rotación en los ejes ortogonales de polarización de la señal que se propaga.
Matemáticamente una lámina de onda se expresa mediante la Ecuación (11) (Leiva et al., 2007).
En esta expresión θ corresponde al ángulo de rotación de los ejes de birrefringencia de la fibra respecto a los ejes de la señal, φ es la diferencia de fase aleatoria producida entre las componentes ortogonales (x, y), ambos ángulos relacionados con el acoplamiento de modos aleatorio, ω es la frecuencia angular y ∆t es el valor del DGD del segmento de fibra.
De esta manera, se puede determinar el pulso de luz a la salida de la fibra conociendo el pulso de entrada, de acuerdo a la Ecuación (12).
De existir acoplamiento de modos aleatorio cada segmento birrefringente tendrá su propia Matriz de Jones y se puede modelar a la cadena de segmentos birrefringentes como la concatenación o producto ordenado de las respectivas matrices asociadas a cada segmento. Si se considera una fibra con k segmentos birrefringentes, la respectiva matriz de Jones vendrá dada por la Ecuación (13).
2.4 Compensación de PMD
La PMD es uno de los principales problemas que afectan a las comunicaciones ópticas actuales a velocidades por encima de los 10 Gb/s, por lo tanto es necesario contar con algún mecanismo que pueda controlar y contrarrestar su efecto sobre la calidad de la transmisión. El problema principal radica en su naturaleza aleatoria, ya que a diferencia de la dispersión cromática, cuyo efecto es predecible, controlable y sus parámetros poseen muy poca variación, la PMD es totalmente impredecible, su magnitud puede variar de un día a otro o incluso en pocas horas, debido principalmente a los cambios de temperatura que alteran la birrefringencia de la fibra y el acoplamiento de modos. Es por estas razones que se requiere un mecanismo de compensación dinámico para controlar y minimizar el valor de la PMD en los enlaces de fibra.
En este trabajo se describe la técnica de post-compensación óptica de PMD. Esta técnica se basa en la colocación de un polarizador-divisor del haz de luz en el receptor cuya función consiste en descomponer el haz de luz en sus dos PSP correspondientes a los ejes rápido y lento de la fibra. Después de la división, cada PSP seguirá un diferente camino. Al PSP correspondiente al eje rápido (el que adelanta al otro) se lo hace pasar por un espejo angular ajustable, cuya función es la de introducir un retardo en la propagación variando su camino óptico para que de esa forma, los retardos correspondientes a cada PSP sean iguales. Una vez logrado esto, ambos PSP se vuelven a mezclar formando así el pulso de luz original. El espejo angular se ajusta de acuerdo al estado de las dos señales entrantes, para lo cual se necesita controlar el espejo por medio de una señal de realimentación (Martin, 2004).
3. SIMULACIÓN DE PMD EN FIBRAS ITU-T G.655
En esta sección se realiza la simulación del fenómeno de PMD para diferentes escenarios usando fibras NZDSF, de acuerdo al estándar ITU-T G.655. El software a utilizarse es OptiSystem 14.2 cuyas características e instrucciones de uso se pueden encontrar en (Optiwave, 2013).
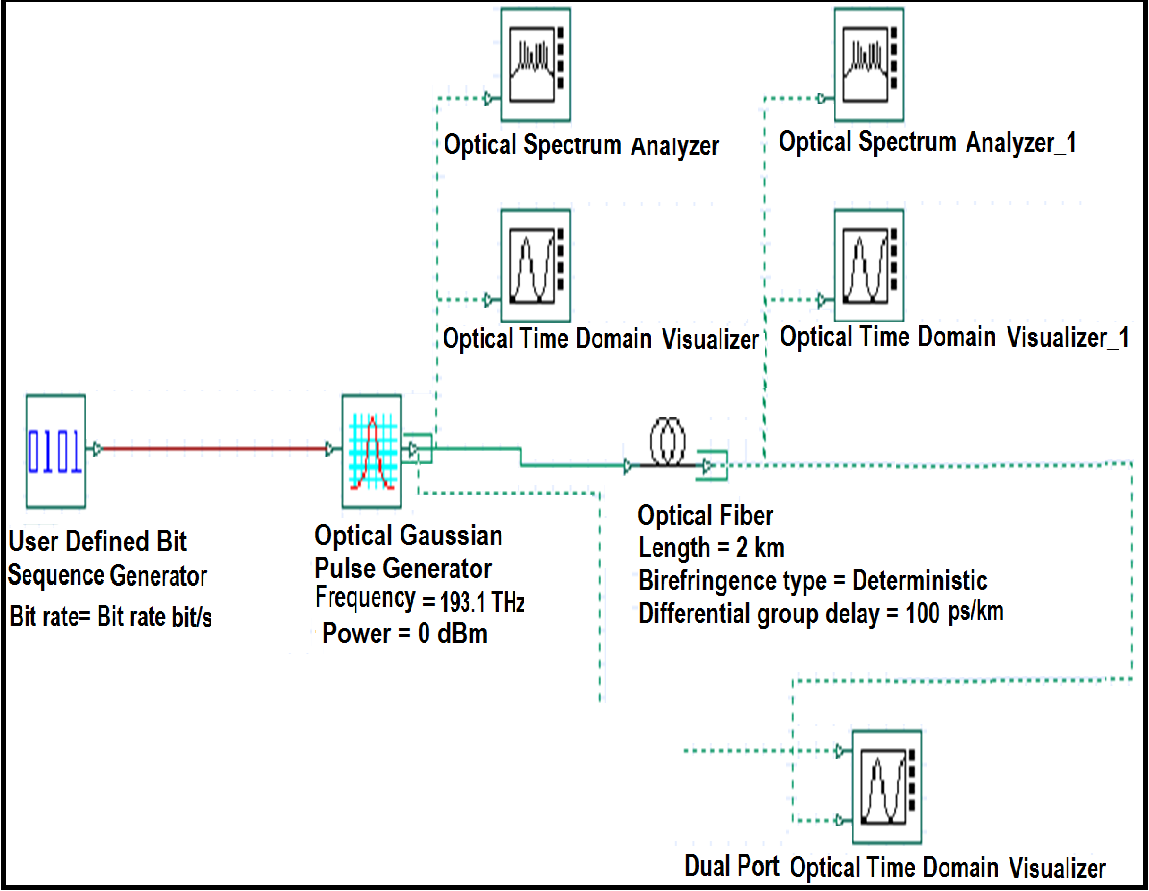
La Figura 3 muestra el entorno de simulación de PMD para los diferentes escenarios de este trabajo.
Para la simulación se plantean diversos casos con diferentes parámetros variables de velocidad de transmisión, longitud de la fibra y valor del coeficiente PMD. Estos escenarios se encuentran descritos en la Tabla 1.
La señal de entrada a aplicarse en cada caso corresponde a un pulso gaussiano de potencia igual a 0 dBm, cuya descripción se puede encontrar en (GCO, 2006). La frecuencia de la señal será de 193,1 THz, valor correspondiente a la frecuencia central de la tercera ventana de transmisión óptica.
Esta señal atravesará un segmento de fibra óptica configurada con los parámetros adecuados de acuerdo a la recomendación ITU-T G.655, siendo monitoreada a la entrada y salida de la fibra, tanto en el dominio del tiempo como en el de la frecuencia.
La idea del entorno de simulación consiste en dar un sentido físico real a las Ecuaciones (13) y (14).
Tabla 1. Escenarios de simulación de PMD
|
|
|
|||||||
| Bit rate (Gb/s) | Longitud de la fibra L (Km) | Longitud de la fibra L (Km) | ||||||
| 100 | 1 000 | 2 000 | 5 000 | 100 | 1 000 | 2 000 | 5 000 | |
| 10 | X | X | X | |||||
| 40 | X | X | X | X | X | X | X | |
| 140 | X | X | X | X | X | X | X | |
A continuación se presentan los resultados obtenidos para cada una de las simulaciones que se incluyen en este trabajo.
3.1 Simulación para: φPMD = 0,3 ps/km1/2, L = 2 000 Km, Vtx = 10 Gb/s
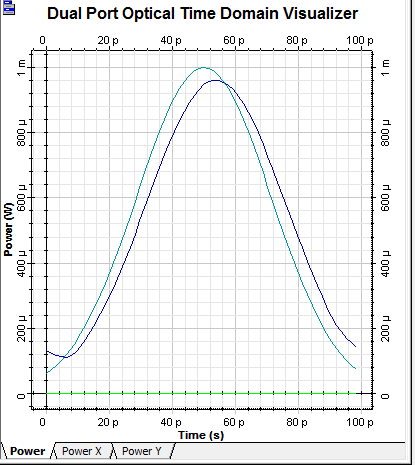
Figura 4. Pulso de entrada (celeste) y pulso de salida dispersado (azul), Vtx = 10 Gb/s y frecuencia 193,1THz .
De acuerdo a (6), el DGD teórico inducido en la fibra es ∆τ=13,42 ps, valor comparable con la décima parte del tiempo de bit del pulso óptico. Por lo tanto, según las recomendaciones de la ITU-T expuestas en (International Telecommunications Union ITU-T, 2009), el nivel de PMD que se espera no es significativo y consecuentemente no afectará a la calidad del pulso óptico.
La Figura 4 muestra el pulso a la salida de la fibra óptica monomodo en color azul, después de sufrir la dispersión por modo de polarización, comparado con el pulso de entrada a dicha fibra en color celeste.
Como se puede observar, el nivel de PMD no afecta en mayor grado a la calidad del pulso de luz, bajo las condiciones de este escenario.
Cabe recalcar que el nivel de PMD no siempre será el mismo (debido a la naturaleza estadística de este fenómeno antes mencionada), por lo tanto la envolvente del pulso de salida variará en cada medición, aunque siempre alrededor del valor promedio de acuerdo a (6).
3.2 Simulación para: φPMD = 0,3 ps/km1/2, L = 2 000 Km, Vtx = 40 Gb/s
El DGD teórico en este escenario de acuerdo a (6), es ∆τ=13,42 ps, valor que en este caso, dada la mayor velocidad, supera la mitad del tiempo de bit del pulso. Por lo tanto, se espera un nivel considerable de dispersión por modo de polarización.
La Figura 5 muestra el pulso a la salida de la fibra óptica ITU-T G.655 en azul, después de sufrir dispersión por modo de polarización, comparado con el pulso de entrada a dicha fibra en celeste.
Como se puede observar, la PMD ha causado un ensanchamiento del pulso de alrededor del 60%; y, una atenuacion debida a la dispersion, del 50%. Nuevamente se enfatiza que estos valores pueden variar debido a la naturaleza estadística de la PMD.
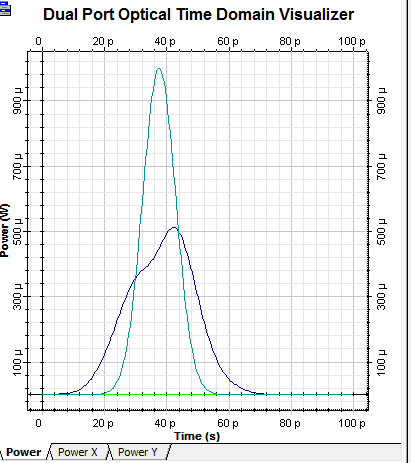
Figura 5. Pulso de entrada (celeste) y pulso de salida dispersado (azul). Frecuencia 193,1 THz y Vtx = 40 Gb/s.
Este grado de dispersión obtenido puede causar un nivel considerable de interferencia entre símbolos (ISI), dificultando el reconocimiento del pulso en recepción e incrementando el BER del sistema.
3.3 Simulación para: φPMD = 0,1 ps/km1/2, L = 5 000Km, Vtx = 140 Gb/s
El DGD teórico en este escenario es ∆τ=7,07 ps, que dada la alta velocidad de transmisión resulta comparable con el tiempo de bit del pulso. Por lo tanto, el nivel de PMD esperado será bastante crítico.
La Figura 6 muestra el pulso a la salida de la fibra en azul, es decir después de sufrir la dispersión por PMD, comparado con el pulso de entrada en celeste. Como se puede observar, el pulso se ha distorsionado totalmente a la salida de la fibra con dispersión PMD, perdiendo la forma de su envolvente, generando prácticamente dos pulsos parciales de amplitud menor al 50% de la del pulso original.
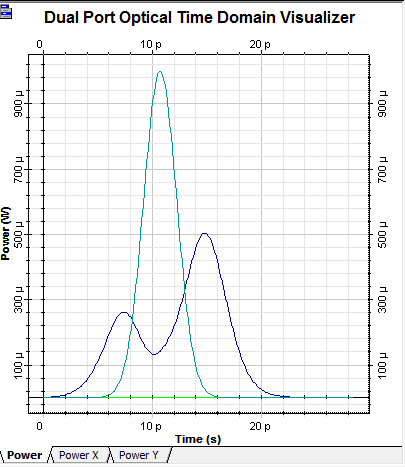
Figura 6. Pulso de entrada (celeste) y pulso de salida dispersado (azul). Frecuencia 193,1 THz y Vtx = 140 Gb/s.
De manera similar a los casos descritos hasta aquí, en la Tabla 2 se incluyen los resultados obtenidos de las simulaciones realizadas para los demás escenarios de simulación que se indicaron en la Tabla 1, señalando los niveles de atenuación y dispersión por PMD porcentuales producidos en cada caso.
Tabla 2. Resultados de la simulación de los diferentes escenarios, comparando los niveles de atenuación y dispersión PMD obtenidos
|
|
|
|||
| Atenuación | Dispersión | Atenuación | Dispersión | |
| <5% | <5% | - | - | |
| 10% | 20% | <5% | <5% | |
| <10% | <10% | - | - | |
| 10% | 20% | <10% | <10% | |
| 50% | 50% | 10% | 10% | |
| 100% | 50% | 30% | 25% | |
| 30% | 40% | 10% | 10% | |
| >100% | 60% | 40% | 30% | |
| >>100% | 80% | 50% | 40% | |
| - | - | 100% | 60% | |
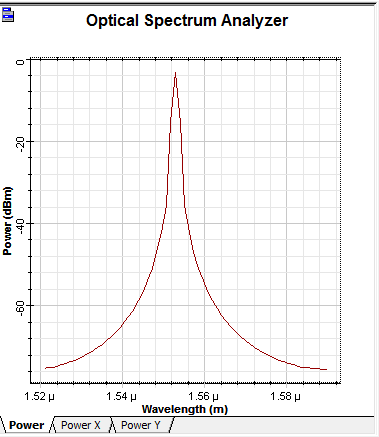
Además, se analizaron los resultados en el dominio de la frecuencia para cada escenario. Se pudo observar que la PMD no afecta al espectro de frecuencias del pulso inicial. Esto se muestra en la Figura 7 para el caso analizado en la sección 3.3, donde se presenta el espectro tanto del pulso de entrada como de salida, observándose que ambos coinciden.
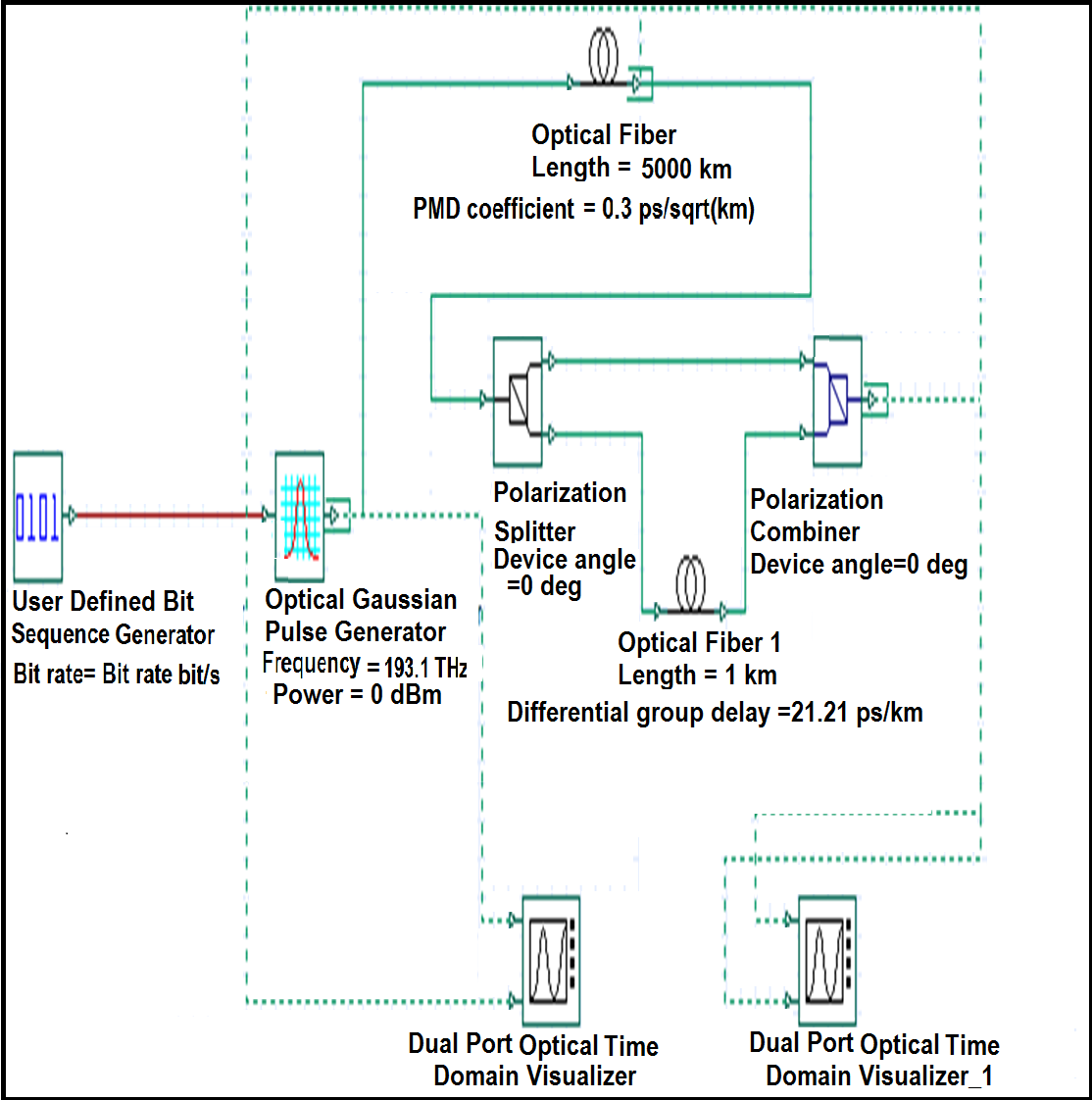
3.4 Simulación de la Compensación de PMD
Para la simulación de la compensación de PMD se utilizó el entorno mostrado en la Figura 8, como se puede observar, el compensador está compuesto por un polarizador divisor, un segmento de fibra Hi-Bi PM que es un tipo de fibra de alta birrefringencia cuyo objetivo es mantener constantes los estados de polarización a lo largo del segmento de fibra, y un mezclador de polarización.
El trabajo del compensador consiste en introducir un retardo previamente configurado al PSP que se adelanta. Este retardo se determinó de acuerdo a la Ecuación (7) y se consigue haciendo que el PSP adelantado recorra el segmento de fibra Hi-Bi PM.
Los escenarios de simulación considerados en este trabajo mantienen fijo el coeficiente PMD característico de una fibra ITU-T G655, mientras se varía tanto la longitud del enlace como la velocidad de transmisión; y, son los siguientes:
-
L = 5 000 Km; Vtx = 10 Gb/s; φPMD = 0,3 ps/km1/2
L = 2 000 Km; Vtx = 40 Gb/s; φPMD = 0,3 ps/km1/2
L = 1 000 Km; Vtx = 140 Gb/s; φPMD = 0,3 ps/km1/2
La Figura 9 muestra los resultados obtenidos de las compensaciones realizadas para el caso de una señal correspondiente a una secuencia de bits “0101101”, donde se puede apreciar el efecto de PMD en una señal que tiene pulsos consecutivos, considerando para dicha secuencia de entrada todos los escenarios de simulación anteriormente indicados.
Para cada uno de los casos antes mencionados, se presenta tanto la señal asociada con la secuencia de pulsos compensados en color azul, como la señal correspondiente a la secuencia de pulsos antes de la compensación en color celeste.
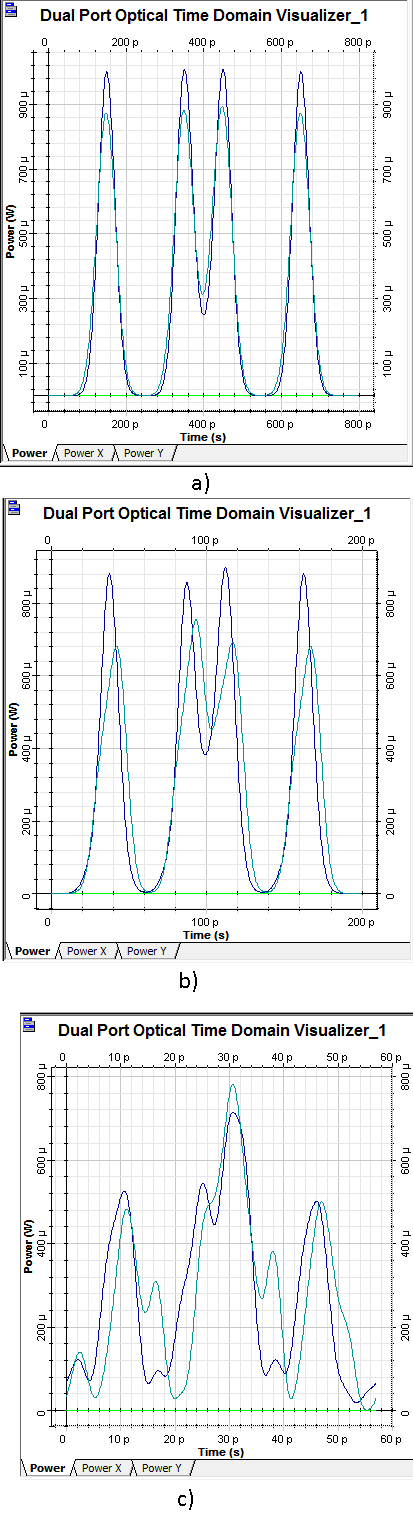
Figura 9. Simulación de la compensación de PMD: a) L = 5 000 Km; Vtx = 10 Gb/s; φPMD = 0,3 ps/km1/2, b) L = 2 000 Km; Vtx = 40 Gb/s; φPMD = 0,3 ps/km1/2 y c) L = 1 000 Km; Vtx = 140 Gb/s; φPMD = 0,3 ps/km1/2.
De acuerdo a los resultados obtenidos en los tres casos, se concluye que esta técnica de compensación es efectiva cuando se tiene velocidades del orden de los 10 hasta los 40 Gb/s, en las que el nivel de dispersión es menor al tiempo de bit del pulso. Sin embargo, mientras más se incrementa la velocidad de transmisión es más difícil realizar la compensación debido a que el DGD del pulso se vuelve comparable al tiempo de bit, como se puede apreciar en la Figura 9 (c), donde la compensación de PMD no es tan efectiva como en los casos en los que se trabaja a menor velocidad.
4. CONCLUSIONES
En fibras ITU-T G.655, PMD es un fenómeno que empieza a ser apreciado en velocidades de transmisión a partir de los 10 Gb/s, pero no es hasta valores superiores, del orden de los 40 Gb/s que su efecto se vuelve considerable, siendo totalmente crítico en velocidades que superen los 100 Gb/s.
Para velocidades de 10 Gb/s, el nivel de PMD no afecta de manera significativa a la calidad de la transmisión, pues los pulsos no sufren distorsiones considerables por PMD al ser transmitidos a estas bajas velocidades.
Para velocidades de 40 Gb/s, la PMD empieza a ser un problema cuando se trabaja con distancias superiores a los 1000 km y coeficientes PMD relativamente altos como los considerados en este trabajo (0,3 ps/km1/2), para menores valores de este coeficiente su efecto es mínimo, de ahí la importancia hoy en día de contar con fibras de bajo PMD.
Para velocidades del orden de los 140 Gb/s, de los resultados obtenidos se observa que se tienen niveles elevados de PMD incluso en distancias cortas. Por lo tanto, los pulsos ópticos son afectados de manera crítica en estas condiciones, siendo necesario a estas velocidades o superiores, que se utilizan en los modernos sistemas de comunicaciones ópticos, que los parámetros PMD de las fibras sean significativamente menores que los requeridos a bajas velocidades, de ahí la importancia de las nuevas categorías UIT-T de fibra con menores coeficientes de dispersión por modo de polarización.
En las simulaciones desarrolladas se observa que a mayor velocidad de transmisión y mayor longitud de la fibra, mayor será la dispersión. Sin embargo, debido a la naturaleza estadística de la PMD, pueden existir casos de gran dispersión con velocidades de transmisión y longitudes de fibra relativamente bajas y viceversa; y, mínima dispersión en escenarios con grandes longitudes de fibra y altas velocidades de transmisión, lo cual se corroboró en simulaciones realizadas que se pueden encontrar en (Cadena, 2017).
El efecto de la dispersión por modo de polarización, no solo generó ensanchamiento del pulso óptico, sino también atenuación debida a la redistribución de la energía que experimenta el mismo. Además, en casos críticos llegó a degradar totalmente la forma de la envolvente del pulso, tornando imposible en casos como estos distinguir dicho pulso de luz en recepción.
Dado que la PMD causa atenuación en los pulsos ópticos, siempre será importante la inclusión de amplificadores ópticos que compensen las atenuaciones propias del sistema de comunicaciones (fibra, empalmes, conectores, splitters, entre otros dispositivos que se utilicen) y las provocadas por este tipo de dispersión.
En casos de dispersión severa, la forma de la envolvente del pulso sufre un nivel alto de degradación, esto ocurre cuando el DGD producido es comparable con el tiempo de bit del pulso. Una buena forma de obtener una transmisión fiable, es asegurar que el DGD teórico no exceda a la tercera parte del tiempo de bit de la señal, tal como se establece en la recomendación de la ITU-T G.663 para fibras monomodo, lo cual fue verificado mediante las simulaciones realizadas en este trabajo.
Para los niveles de potencia usados en este trabajo, que corresponden a valores típicos utilizados en sistemas de comunicación ópticos reales, la PMD no ha tenido efecto sobre las componentes de frecuencia de la señal que se propaga; por lo tanto, la señal vista en el dominio de la frecuencia será la misma a la entrada y salida del segmento de fibra.
Debido a su naturaleza estadística, el valor del DGD observado en un determinado caso, no será el mismo en todos. En enlaces reales, un valor medido en una determinada hora del día puede variar en la siguiente.
El uso de técnicas de post-compensación de PMD ópticas pasivas es bastante efectivo cuando el nivel de dispersión, comparado con el tiempo de bit de la señal, es relativamente bajo (DGD ≈ 1/2 tB), como se pudo comprobar en las simulaciones realizadas. Sin embargo, cuando la dispersión del pulso es comparable con el tiempo de bit, estos métodos se vuelven inefectivos.
Las técnicas de post-compensación pasivas en fibras ITU-T G.655 se dificultan por la birrefringencia de naturaleza estadística que caracteriza a las fibras ópticas.