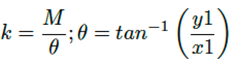Metodología

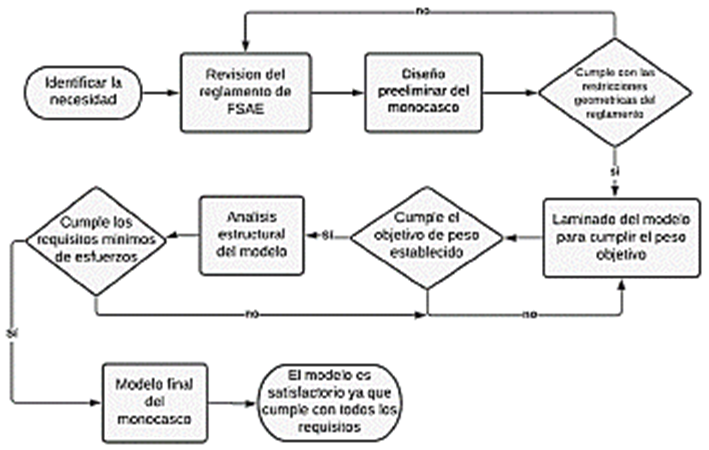
Luego de realizar un análisis del estado del arte se elabora un flujograma en el cual se establece el orden y las actividades que conciernen al diseño, análisis estructural y optimización del peso del modelo.

En la primera etapa se revisa la reglamentación de FSAE para extraer los parámetros más influyentes sobre el diseño y restricciones del monocasco [11]. En la segunda etapa se diseña el modelo tomando en cuenta las restricciones previas del reglamento [12].

Con el modelo completo en la Figura 1, en la etapa tres se procede al laminado CFRP en el que se establece el espesor que tendrá el modelo final, el laminado va a depender de la sección en la que se trabaja, ya que cada sección tiene un espesor diferente por los esfuerzos que soportará cada zona.

Lo referente a los análisis de resultados se detallará en la siguiente sección que corresponde al desarrollo de la metodología planteada.

Figura 1 Modelo final en superficies 

Materiales

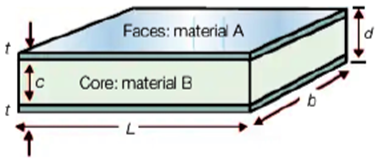
Los materiales a utilizar en el análisis son refuerzos de tela de fibra de carbono en una estructura de sándwich, Figura 2, con Honeycomb. La unión de diferentes materiales se conoce como materiales compuestos, proveen de una gran resistencia mecánica a esfuerzos y una muy buena disipación de esfuerzos a través de la estructura. Este panel de sándwich se compone de tres componentes principales, un núcleo, una matriz y las fibras que en este caso son de fibra de carbono [4].

Figura 2 Típica estructura de sándwich [4] 

Fibras

Los elementos hechos de materiales compuestos de fibra, se pueden diseñar para cada caso de carga, por lo que el material se crea de acuerdo con los requisitos estáticos requeridos. Existe la opción de elegir las direcciones en las que se colocarán las fibras. Apilar láminas de fibra de carbono con diferentes direcciones, le da al material las propiedades deseadas en cualquier dirección. Las orientaciones que se le dará a las fibras en el plano serían de 0°, 90° y ±45° [5].

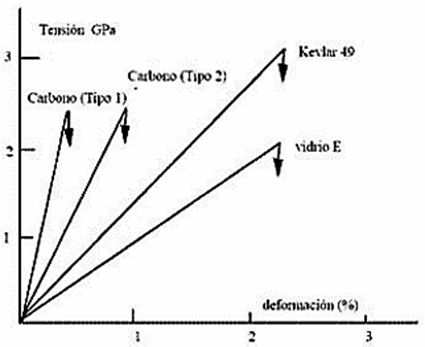
En la Figura 3 se puede ver que la fibra de Kevlar es la más resistente, mientras que la fibra de carbono es la más rígida. La fibra de vidrio es la menos resistente y menos rígida, pero a su vez es la más económica de las tres.

El uso de estos materiales en competición ofrece una gran ventaja en términos de peso total. Es posible realizar una estructura con una rigidez similar a la de una estructura metálica convencional e incluso reducir su peso a la mitad. Por ello, su uso en equipos que buscan buenos resultados es fundamental [5].

Figura 3 Diagrama tensión-deformación de fibras [5] 

Matriz

La matriz es el material que soporta todas las fibras y representa su unión. Las fibras se impregnan en la matriz y forman un solo material.

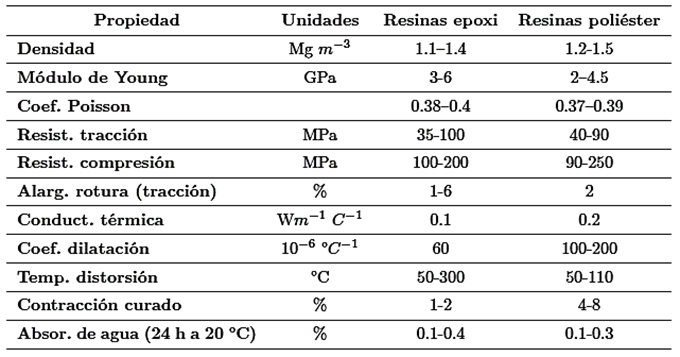
Actualmente, se utilizan dos tipos principales de resinas para la matriz, epoxi y poliéster. Ambas son térmicamente estables, lo que significa que no se derretirán con el calor, simplemente pierden ciertas propiedades de rigidez. Otra propiedad es que su comportamiento estructural es isótropo, esto quiere decir que tiene las mismas propiedades físicas en todas las direcciones. Para el presente proyecto se aplicó una resina epoxi.

En la Tabla 1 se referencian algunas propiedades de las resinas.

Tabla 1 Propiedades de resinas [5] 

Núcleo de Honeycomb

Hay diferentes tipos de núcleos de material de Honeycomb. Cada tipo tiene diferentes propiedades dependiendo del material del que sean fabricados; los más comunes son hechos de aluminio, papel de aramida (Nomex), acero, fibra de vidrio, carbón o cerámica [14]. El núcleo de Honeycomb consiste en un patrón simétrico hexagonal como se ve en la Figura 4, esta estructura provee propiedades relativamente altas a la compresión y resistencia a la rotura, combinadas con baja densidad [6].

Figura 4 Estructura con celdas hexagonales [6] 

En este estudio, para el núcleo se selecciona Honeycomb de aluminio que presenta una gran propiedad de absorción de energía, el espesor de este núcleo es de 20 mm.

Determinación del modelo CAD

El diseño del modelo parte de las regulaciones del percentil masculino 95, las cuales se detallan a continuación.

Partiendo de una buena posición vertical y horizontal del volante, el ángulo del asiento, la posición de los pedales, las barras de seguridad, buscando la comodidad para el piloto [9]. En la Figura 6 se muestra la plantilla del percentil 95 masculino. Los valores de distancias se detallan en el reglamento FSAE [11].

Figura 6 Plantilla del percentil 95 masculino [15] 

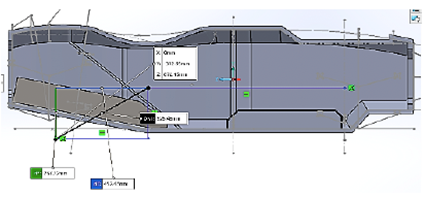
Una vez determinados los percentiles y las dimensiones mínimas de la apertura de la cabina y la sección mínima transversal, se ha realizado el primer dimensionamiento, en el que se basa el diseño del monocasco. La Figura 7 muestra las aperturas transversal y de la cabina.

Figura 7 Sólido de apertura de la sección transversal interna en perspectiva isométrica [15] 

Las medidas de estas secciones se encuentran detalladas a continuación:

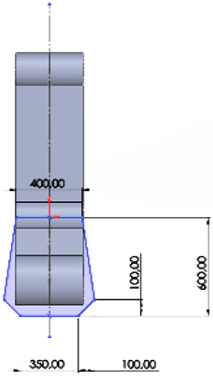
Apertura de la cabina (Figura 8)

Figura 8 Dimensiones de la apertura de la cabina [15] 

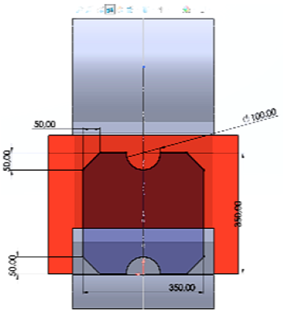
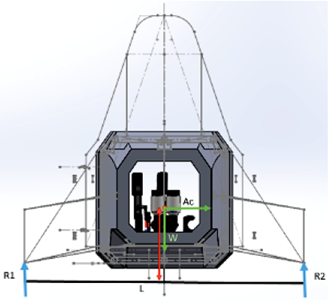
Sección transversal interna (Figura 9)

Figura 9 Dimensiones de la sección transversal interna [15] 

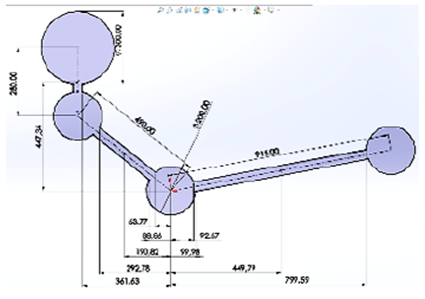
Con estas medidas se desarrolla un modelo con los elementos principales que se encuentran en el monocasco, dichos elementos son la batería que se encuentra en la parte posterior, un inversor debajo de las piernas del piloto y un par de cortafuegos. En la Figura 10 se observa el boceto lateral principal.

Figura 10 Disposición de elementos y boceto lateral [15] 

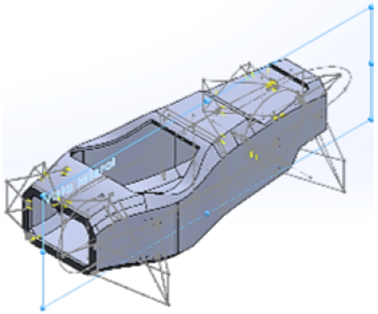
De este boceto nace el modelo CAD, donde se colocan los puntos de sujeción de algunos elementos en el monocasco; el diseño final se ve en la Figura 11.

Figura 11 Diseño final del monocasco [15] 

Con el modelo final, se obtiene el centro de gravedad y esfuerzos que se detallan a continuación.

Determinación del centro de gravedad

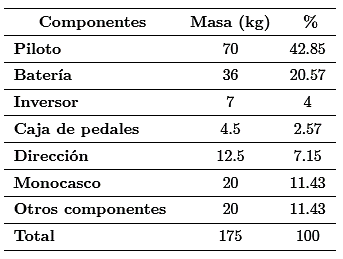
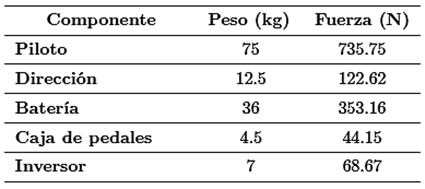
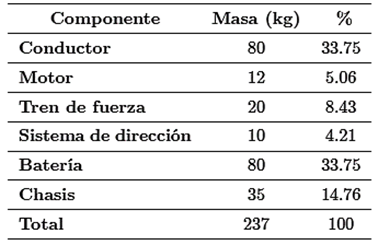
En esta sección, se aplican los pesos sobre el monocasco en el software. Posterior a esto, se realiza un ensamble con los componentes más representativos que se seleccionaron para el cálculo y listados en la Tabla 2. Con la herramienta de propiedades físicas, se localiza la posición del centro de gravedad del prototipo ensamblado visto en la Figura 12.

Tabla 2 Masas aproximadas del vehículo [10] 

Figura 12 Ubicación del centro de gravedad [15] 

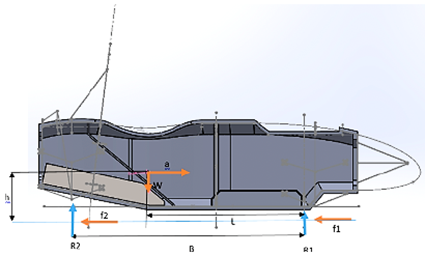
Transferencia de masa lateral

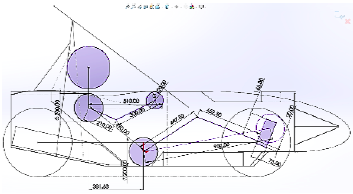
Para desarrollar este cálculo, se tiene en cuenta el vehículo describe una curva que actúa sobre el centro de gravedad con una aceleración centrífuga equivalente a 4 G. La Figura 13 describe el diagrama de cuerpo libre en el que se definen el centro de gravedad y la dirección de las cargas.

Figura 13 Diagrama de cuerpo libre [15] 

La reacción R2 es la carga que interviene en la rigidez torsional, este torque se aplica en direcciones opuestas en ambos lados del eje delantero, para la simulación se utilizó un valor de 6870 N para simular una carga mayor en el monocasco y demostrar la dureza del material [11].

Transferencia de masa longitudinal y de frenado

Esta es la transferencia de masa longitudinal en la dirección de los neumáticos delanteros, que resulta de las fuerzas de frenado. La Figura 14 muestra el diagrama de cuerpo libre para este esfuerzo.

La velocidad máxima, el coeficiente de fricción entre los neumáticos y el asfalto, la posición del centro de gravedad, el tiempo de frenado y el peso del vehículo, se determinan como condiciones de iniciales.

Figura 14 Diagrama de cuerpo libre longitudinal [15] 

Las cargas calculadas R1=1423.85 N y f1=1181.79 N involucradas en el estudio de las pruebas de resistencia longitudinal y de frenado; se toman como referencia, sin embargo, en la simulación, todos los valores se incrementan, con el fin de tensionar aún más el modelo.

Caso de impacto lateral

Inicialmente, se supone que la velocidad del vehículo es de 40 km/h, teniendo en cuenta el peor de los casos y aplicando una fuerza de 4,5 G en el impacto. Para el cálculo se utiliza un peso del vehículo de 220 kg y un peso del conductor de 75 kg [15]. Al aplicar la fórmula de velocidad final, con una velocidad final de 11.11 m/s, que equivale a una velocidad inicial que parte del reposo, más la multiplicación de la aceleración, en este caso siendo el dato a despejar, con el tiempo de 0.3 s; esto al despejarse con respecto a la aceleración se obtiene 37.03 m/s2. Con el dato de la aceleración obtenida, se calcula la fuerza que será el resultado de la aceleración por la masa de 290 kg; lo que da un resultado de 10 739.66 N. Esta es la fuerza que se usará para la simulación de impacto lateral [16].

Preparación del modelo en ANSYS ACP

El software ANSYS provee la herramienta de Composite PrePost (ACP) para facilitar la construcción del modelo de elementos finitos y acceder a los resultados.

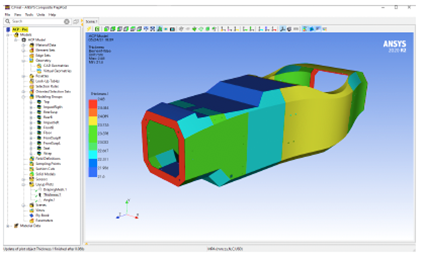
Los modelos reales construidos en materiales compuestos tienen varias capas y numerosos materiales, por eso es fundamental preparar el modelo MEF con la correcta dirección de las capas y apilado de materiales [17].

En la Figura 15 se muestra el modelo final con las capas en ANSYS ACP.

Figura 15 Modelo acabado en ANSYS ACP [15] 

Análisis de la rigidez torsional del modelo mediante MEF

La rigidez torsional está definida físicamente por las siguientes ecuaciones, en este apartado se determina, mediante un análisis MEF, la deformación total. La figura 16 presenta cómo se mide los valores y1,x1. [18]

Donde:

M = Momento torsional (N*m)

θ = Ángulo de deformación (grados)

x1 = Distancia horizontal desde el plano central del vehículo al punto donde se mide la deformación y1

y1 = Deformación en sentido vertical

K = rigidez torsional (N*m⁄grados)

Figura 16 Distancia x1 y y1 [15] 

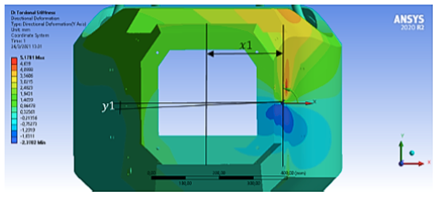
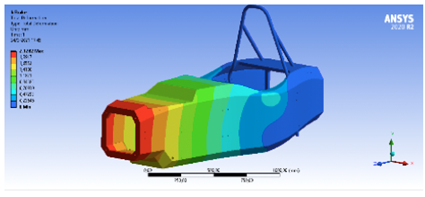
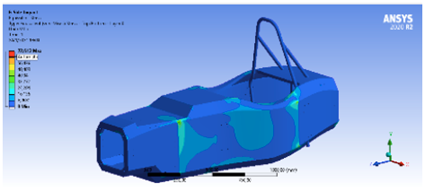
Para esta simulación se aplicó una fuerza de 6870 N y se obtiene una deformación media de 1.001 mm y una máxima de 4,2 mm (ver Figura 17), donde el esfuerzo está más concentrado. Tiene una deformación máxima de 5,3 mm por encima del punto de suspensión superior.

Figura 17 Deformación de rigidez torsional [15] 

Análisis de rigidez longitudinal

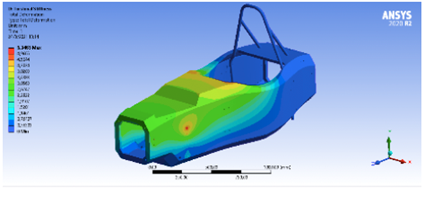
Para analizar esta deformación, se aplica una carga de 2500 N sobre el eje delantero, se determina una deformación de 1.99 mm, como se ve en la Figura 18.

Figura 18 Deformación en rigidez longitudinal [15] 

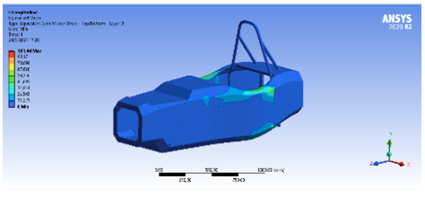
En cuanto al esfuerzo sobre la estructura, el máximo es de 101.44 MPa, como presenta la Figura 19. El esfuerzo es bajo, porque la estructura permite una buena distribución a través de toda la estructura.

Figura 19 Esfuerzos longitudinales [15] 

Análisis de frenado

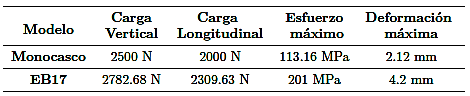
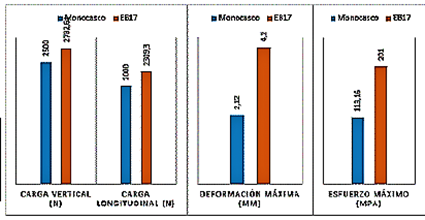
En este análisis se aplican dos cargas sobre el eje delantero con un valor de 2500 N en sentido vertical y 2000 N en sentido longitudinal; la deformación máxima es igual 2.12 mm, como se ve en la Figura 20.

Figura 20 Deformación en el frenado [15] 

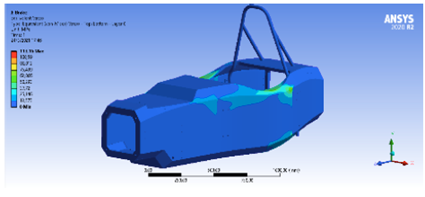
En cuanto al esfuerzo máximo en la estructura esde 113.16 MPa, el cual no lleva al límite de rotura del material, como presenta la Figura 21.

Figura 21 Esfuerzos en el frenado [15] 

Análisis de impacto lateral

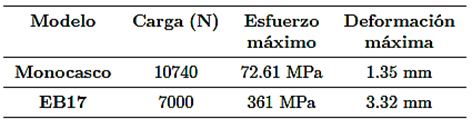
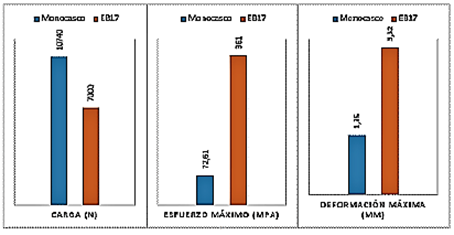
El valor a utilizar en este esfuerzo es de 10 739.66 N detallado en la sección 3.53 [15], la deformación máxima como se ve en la Figura 22, es de 1.35 mm.

Figura 22 Deformación de impacto lateral [15] 

En cuanto al esfuerzo sobre la estructura, alcanza un máximo de 72.61 MPa lo cual indica que se distribuye de mejor manera a través del monocasco, como se ve en la Figura 23.

Figura 23 Esfuerzos de impacto lateral [15] 

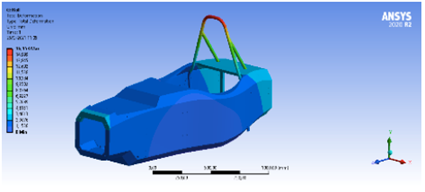
Simulación de vuelco

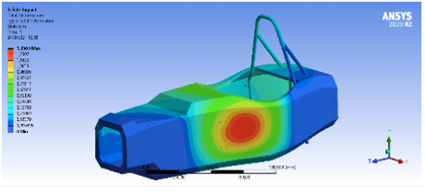
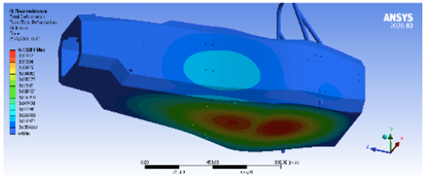
En esta simulación son aplicadas tres cargas, una longitudinal, una transversal y una vertical de 6 KN, 5 KN y 9 KN, respectivamente; los resultados conseguidos demuestran un valor máximo de deformación de 16.15 mm (Figura 24) y el esfuerzo máximo presente es de 426.52 MPa (Figura 25) [19].

Figura 24 Deformación del Main Hoop [15] 

Figura 25 Esfuerzos en el Main Hoop [15] 

Simulación de peso en el suelo

En esta simulación se ubica el peso distribuido de los elementos, sobre todo, el suelo del monocasco. La Tabla 3 detalla el peso de los elementos y la fuerza ejercida de los mismos.

Tabla 3 Peso de los elementos sobre el monocasco [15] 

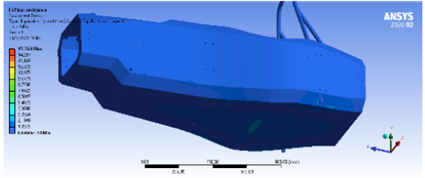
Los resultados de esta simulación muestran que la deformación máxima en el piso del monocasco es de 0,13 mm (Figura 26) y una tensión máxima de 15 Mpa (Figura 27).

Esto indica que el material puede soportar perfectamente el peso de los elementos.

Figura 26 Deformación del suelo [15] 

Figura 27 Esfuerzos en el suelo [15] 

Validación de datos

Eficiencia del diseño en cuanto a reducción de peso

Sobre la base de los datos obtenidos, se pasó al análisis de eficiencia en cuanto a la reducción de peso que debería tener el prototipo.

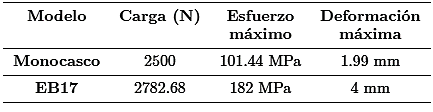
El modelo EB17 se utiliza como objeto de comparación con el diseño del prototipo de este trabajo [10].

Con la Tabla 4 indicada, se concluye que el peso del chasis y carrocería tendrían un valor de 55.31 kg entre ambos, que representa el 23.54 % del peso total [15].

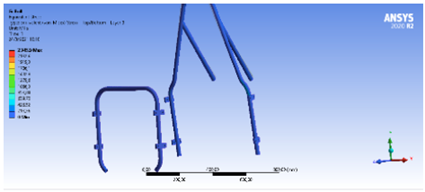
En las estructuras del Main y Front Hoop, el material a aplicar es “AISI 4130 acero normalizado a 870 °C”; los datos se tomaron de la simulación del EB17.

Tabla 4 Masas aproximadas del EB17 [10] 

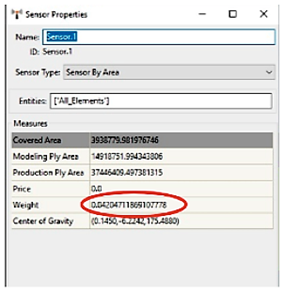
Como se observa en la Figura 28, por medio del software se obtuvo un peso reducido a 4 decimales de 0.0420 t equivalentes a 42 kg, sin el uso del triángulo de seguridad en el programa ANSYS, al sumar los datos del triángulo de seguridad se obtendría 48.19 kg de peso entre los tres elementos combinados [15].

Figura 28 Peso preliminar del monocasco obtenido de ANSYSACP [15] 

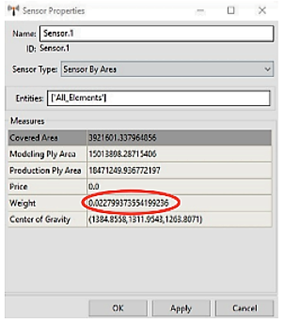
Para un análisis final, se obtuvo el peso del monocasco, optimizando las capas del modelo, como se demuestra en la Figura 29 En esta ocasión, con sus estructuras triangulares se obtuvo un peso de 0.0227 t (22.7 kg), que reduce casi la mitad del peso inicial.

La integración de los elementos de seguridad incrementó su factor de seguridad y fue capaz de reducir capas de material y así optimizar aún más su peso. Junto con su triángulo de seguridad, el peso final es de 27,2 kg. Un análisis final de su optimización de peso muestra que hay una reducción significativa en comparación con el EB17, que tendría 237 kg, de los cuales 55,31 kg son el peso del chasis y la carrocería. El monocasco, tendría un peso final de 27,2 kg, lo que se traduce en una optimización en cuanto a reducción de peso del 47,2 %, lo que supondría 28,11 kg menos para el teórico monoplaza.

Figura 29 Peso final del monocasco obtenido de ANSYSACP [15] 

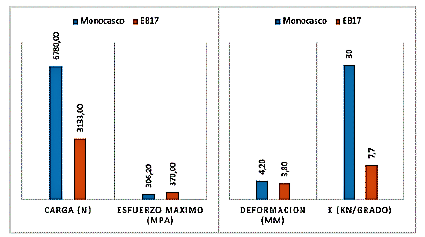
Comparativa de rigidez torsional

El monocasco tiene una mejor disipación de la tensión a una carga 2,1 veces mayor que el modelo EB17 y tiene una concentración de tensión un 17 % menor. Se tiene el valor K, que determina la rigidez torsional, para el monocasco de 75 % superior al EB17 (Tabla 5), lo que determina la estabilidad del vehículo en curvas, Figura 30.

Tabla 5 Rigidez torsional de los modelos [15] 

Figura 30 Resultados rigidez torsional [15] 

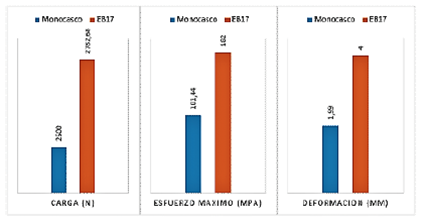
Comparativa de rigidez longitudinal

El monocasco tiene un 11 % menos de carga aplicada en la simulación, lo que significa que el monocasco disipa mejor las tensiones porque tiene un 45 % menos de concentración de esfuerzos y 50 % menos de deformación en comparación con el EB17 (Tabla 6 y Figura 31).

Tabla 6 Comparativa rigidez longitudinal [15] 

Figura 31 Resultados rigidez longitudinal [15] 

Comparativa de frenado

En este análisis intervienen cargas que actúan sobre las ruedas delanteras, con una carga vertical y longitudinal al vehículo (Tabla 7 y Figura 32).

Tabla 7 Análisis de frenado [15] 

Figura 32 Resultados de frenado [15] 

Comparación de impacto lateral

Las cargas en el monocasco son 11 % en la carga vertical y 14 % en la carga longitudinal, la disipación de esfuerzos es mayor en el monocasco, ya que tiene 44 % menos de concentración de esfuerzos que el modelo EB17; la deformación en el monocasco es de 44 % menor que el EB17. (Tabla 8 y Figura 33)

Tabla 8 Análisis impacto lateral [15] 

Figura 33 Resultados impacto lateral [15] 

Como se puede apreciar, el monocasco tiene mejor disipación de tensiones en su estructura, pues la carga es un 53 % mayor que el modelo EB17 y tiene un 80 % menos de acumulación de tensiones, de igual manera la deformación que presenta el monocasco es un 60 % menor que su modelo antecesor.