1. INTRODUCCIÓN
Las técnicas espectroscópicas de mezcla de cuatro ondas (FWM por sus siglas en inglés) degenerada y no-degenerada han sido empleadas de muy variadas maneras en las últimas décadas. Destacamos como esta técnica ha sido utilizada para estudiar polímeros (Singh y col. 1988), moléculas biológicas (Sugisaki y col. 2007), clusters de semiconductores de tamaño nanométrico (Wang, 1991), excitones (Abramavicius y col., 2007), siendo particularmente útil en la descripción de los datos no lineales cuando el sistema molecular tiene una fuerte interacción con su medio en presencia de campos electromagnéticos. Más recientemente, Al-Saidi y Abdulkareem (2016) han reportado cambios en las propiedades ópticas de una solución química, debido a la concentración molecular del colorante estudiado. En este caso, la respuesta del sistema al cambio de la concentración molecular se produce por la elevada absorción saturable no lineal inducida, de importancia para el desarrollo de dispositivos no lineales, como limitadores ópticos. Por otro lado, Sudheesh y col. (2013) han reportado un estudio sobre el tercer orden no lineal, propiedades ópticas de una nueva clase de fenilhidrazonas y la influencia de las nanopartículas de plata y oro en su respuesta no lineal. Experimentos de FWM han sido muy útiles para extraer información espectroscópica de los tiempos de relajación longitudinal y transversal (Yajima y Souma, 1978; Souma et al, 1980). En estos experimentos, las ondas incidentes que se propagan interactúan con el medio molecular, generando una señal no lineal. En mezcla de cuatro ondas (FWM), dos haces láser (campo de bombeo con frecuencia ω1 y campo de prueba con frecuencia ω2) se enfocan sobre el medio resonante, generando una señal con frecuencia
En la mayoría de los casos, los efectos radiativos no son ciertamente la única fuente y, por lo general, no son la fuente dominante de fluctuaciones e incoherencias de relajación. Si el mecanismo de relajación implica cambios en la frecuencia de transición del sistema molecular que persisten tras una interacción entre la molécula-activa y la perturbación electromagnética, las ecuaciones que rigen la evolución temporal son de naturaleza integro-diferencial y las OCBE ya no son válidas. Normalmente la frecuencia de transición en el par de estados moleculares se considera como un parámetro. Esta suposición es válida sólo en casos de interacción débil entre solutos y disolventes, en cuyo caso puede generarse una línea de absorción homogéneamente ensanchada. Sin embargo, si uno está interesado en el desarrollo de la radiación de un sistema de dos niveles impulsado por un campo monocromático y sumergido en un medio condensado o reservorio térmico, la suposición ya no es válida. En el presente trabajo de revisión, y bajo estas consideraciones, y tras el cálculo de la coherencia y susceptibilidad del sistema, hemos analizado las respuestas ópticas para un modelo estándar de un colorante orgánico mediante espectroscopia de mezcla de cuatro ondas. Tanto en los casos de mezcla de cuatro ondas de frecuencias degeneradas como las no degeneradas, han sido ampliamente aplicadas durante varios años, y más recientemente, han sido objeto de renovado interés en el campo de la nanociencia, donde este tipo de espectroscopia se utiliza para determinar la estructura de los nanomateriales a través de sus respuestas ópticas no lineales. Estos estudios están aún en desarrollo, prometiendo abrir una intensa línea de investigación, donde los modelos que proponemos tienen una amplia aplicación. Nuestro grupo de investigación, ha empleado diferentes metodologías para resolver la OSBE y obtener expresiones que permitan la comprensión de los perfiles ópticos de absorción y dispersión con el fin de caracterizar los sistemas moleculares en estudio.
Para efectos del presente trabajo, nuestros estudios pueden ser presentados de la siguiente forma: a) métodos de perturbación como una forma de cuantificar los efectos de saturación por parte del campo intenso de bombeo, con el fin de obtener expresiones analíticas de los elementos de la matriz densidad reducida (Paz y Mendoza-García, 2012; Colmenares y col., 1995; Mastrodomenico y col., 2008; Paz y col., 2017 y Romero-Depablos y col., 2009); b) efectos de la distribución de probabilidad de la forma de línea de absorción (Mendoza-García y col., 2010); c) consideraciones sobre la estructura molecular de un modelo de molécula simple de dos estados. Distinguimos aquí, los efectos del cruce de curvas en acoplamientos vibrónicos en la aproximación diabática (Paz y col., 1994; García-Sucre y col., 1994; Squitieri y col., 1994; García-Sucre y col., 1993), y los efectos de la difusión espectral en estados electrónicos con alta densidad de estados vibro-rotacionales (García Golding, 1983; Mourou, 1975; Yajima y col., 1978). Precisamente entender la naturaleza de la estructura molecular y los procesos de relajación cuando un sistema molecular interactúa con una radiación láser, y caracterizar este último formalmente, permitió reconocer a Gerard Mourou en 2018 con el Premio Nobel en Física.
Dada la complejidad en la formulación de un modelo que considere simultáneamente estos estudios, presentaremos en este trabajo los aspectos más relevantes de cada una de estas propuestas. En todos nuestros resultados es evidente que las propiedades ópticas no lineales son muy sensibles a la presencia del solvente, al tipo de tratamiento perturbativo de los campos electromagnéticos, al mecanismo de relajación inducido, al cruce de las curvas de potencial de los estados electrónicos iniciales y, finalmente, a la alta densidad de estados en el mecanismo de difusión espectral. El efecto de cruce de curvas por Hamiltonianos residuales del tipo spin-orbita, el cual deriva en un acoplamiento intramolecular, no será considerado en este trabajo en vista de la complejidad que se presenta cuando se trata simultáneamente este efecto vibrónico con los derivados del baño térmico. Nuestros resultados permiten estudiar con mayor precisión la correlación entre los efectos de la estructura molecular con la respuesta óptica generada. Los efectos saturativos del campo electromagnético, simetrías en el coeficiente absortivo y procesos de difusión espectral intra e interbanda, son algunas de las consideraciones que permitirán una caracterización más completa de los sistemas moleculares complejos.
2. CONSIDERACIONES TEÓRICAS GENERALES
La dinámica de un sistema de dos niveles, definidas por los estados electrónicos
Hemos seleccionado esta forma de establecer la dinámica de los estados del sistema, ya que permite incluir la simultaneidad de los efectos del reservorio térmico de manera estocástica (con un desplazamiento de la frecuencia de Bohr) y la interacción radiativa por efectos del campo electromagnético. El desplazamiento seleccionado de la frecuencia de Bohr a una frecuencia dependiente del tiempo está sujeto a procesos multiplicativos y bajo consideraciones expresadas de acuerdo con el teorema de límite central.
3. METODOLOGIAS Y RESULTADOS
Con el fin de agrupar el conjunto de resultados o las distantes variantes en el cálculo de las propiedades ópticas no lineales, presentamos un esquema general el cual supone iniciar con la ecuación de Liouville y Von-Newmann para la matriz densidad, y resolver el problema de sus elementos de matriz tanto en el dominio de tiempo como en el de frecuencias, y a partir de allí seguir una ruta de cálculo relativamente equivalente.
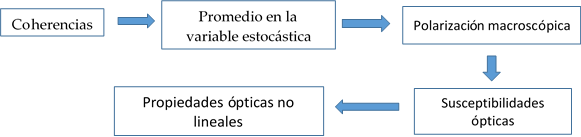
Figura 1. Bajo este esquema podemos incluir: formas perturbativas del campo, efectos de saturación, distintas anchos de líneas, efectos de difusión espectral y acoplamiento intramolecular en la descripción de la estructura
3.1 Perturbación y Cálculos de Coherencias a Tercer Orden en las OSBE
En este estudio, las OSBE fueron desarrolladas hasta el tercer orden en la coherencia, obteniendo como resultado un conjunto de ecuaciones diferenciales acopladas, de la forma:
Donde se han definido los siguientes elementos:
Donde
Donde
Aplicamos la metodología propuesta por Colmenares y col. (1995) para la resolución de estas ecuaciones diferenciales estocásticas, consideramos la aproximación de la onda rotante (Paz y col, 2015) (RWA por sus siglas en inglés) y seleccionando únicamente términos con frecuencia cercana a ω_3, obtenemos las coherencias
Donde las funciones dependientes de las desintonizaciones en frecuencia bombeo-prueba vienen dadas por
Donde es posible definir
En la ec (7) hemos considerado que la polarización no lineal macroscópica inducida está dada por
Usando la ecuación de Maxwell
En ambos coeficientes hemos considerado la aproximación de variación suave para la envolvente del campo electromagnético. Para el estudio de las respuestas ópticas no lineales, seleccionamos el colorante orgánico Cloruro de Malaquita Verde, dado su amplio uso experimental, además del comportamiento a través de un esquema de dos niveles, y el conocimiento pleno de los parámetros que lo caracterizan relacionado con sus mecanismos de disipación. Empleamos para el modelaje y cálculo de las respuestas ópticas los siguientes parámetros:
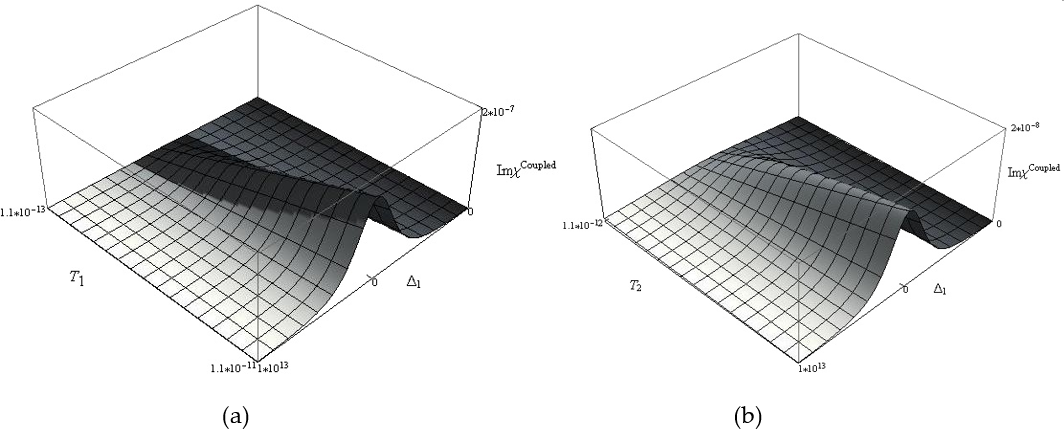
Figura 1. Coeficiente de absorción no lineal como función del desintonizamiento Δ_1 y de los tiempos de relajación transversal: a) γ=0 y b) γ=1.1×10^12
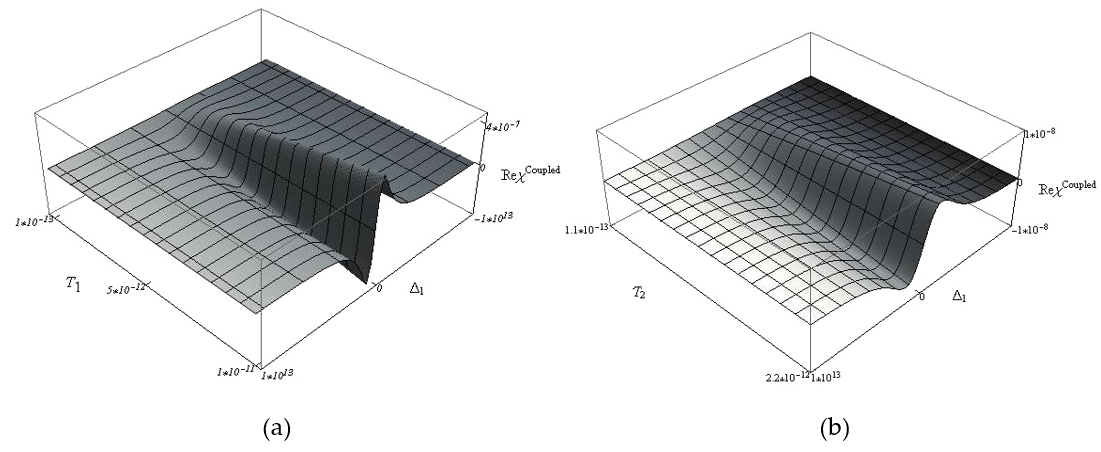
Figura 2. Índice de refracción no lineal como función del desintonizamiento de bombeo Δ_1 y de los tiempos de relajación: a) γ=0 and b) γ=1.1×10^12
En la Figura 2 hemos considerado el agua como solvente, con índice de refracción 1,333. El perfil de dispersión varía asimétricamente alrededor de este valor, siendo coincidente únicamente en la región de resonancia. El tratamiento que hemos realizado refleja el comportamiento de los coeficientes dispersivos y absortivos no lineales en este espacio de desintonización y relajación, cuando la incidencia perturbativa es tan sólo al mínimo orden. Esto es, la señal generada de FWM requiere una oscilación de poblaciones al segundo orden. Hemos resuelto el problema en el dominio del tiempo para la matriz densidad reducida y finalmente, evaluamos las componentes de Fourier para el cálculo de polarización. Con esta forma, hemos evitado los incidentes de correlación que se presentan a dos tiempos distintos entre el campo electromagnético y la respuesta por parte de la susceptibilidad macroscópica, esto es, la integral de polarización dada por
3.2 Efectos de Saturación por Parte del Haz de Bombeo
El formalismo que a continuación se presenta establece un tratamiento igualitario para los haces de débil intensidad (prueba y señal), pero define un tratamiento del haz de alta intensidad que perturba el sistema molecular, bajo un esquema perturbativo, con desarrollos en serie de muy alto orden. Esto define lo que en la literatura se conoce como efectos de saturación por parte del bombeo. No se pretende ir adicionando términos de perturbación en la serie e ir resolviendo el problema. Se ha diseñado una metodología en la cual no se establece a priori la condición para la amplitud del bombeo, sino que se restringe el orden total, dependiendo del proceso fotónico, sujeto a la no violación de la aproximación de onda rotante. Es esta última la que condiciona el término a considerar, lo cual incluye esquemas de desarrollos infinitos para las amplitudes en el haz de bombeo. Seguimos manteniendo la presencia del reservorio térmico a través del corrimiento de la frecuencia de resonancia determinista empleando el tratamiento de Liouville en la matriz densidad reducida. Los tratamientos de saturación inducidos por “Efectos de altas potencia de bombeo” High-pump-power effects” serán considerados en el dominio de Fourier. A diferencia del caso anterior y en vista de su complejidad de cálculo, la ecuación dinámica
Para la componente de frecuencia cero de la diferencia poblacional
Escogemos
Para llevar a cabo los promedios mencionados anteriormente, Van Kampen (1981) ha propuesto un método en el que resuelve formalmente la ecuación diferencial estocástica asumiendo que es determinista, y luego toma un promedio sobre las realizaciones de la variable estocástica. Un enfoque diferente consiste en tomar el mismo promedio antes de resolver las ecuaciones ópticas de Bloch (OBE por sus siglas en inglés). En este último caso, el conjunto de ecuaciones diferenciales obtenidas puede describirse como un proceso Ornstein-Uhlenbeck (OUP). En este trabajo, resolvemos las OBE como si fueran deterministas y luego, reconociendo el hecho de que depende de las realizaciones de
En la aproximación tensorial, obtenemos:
Donde M es un orden requerido para garantizar la convergencia de esas expresiones. Hemos definido además
Donde el término para n = 0 viene dado por:
erf(u) es la función error evaluada en u, y en la que hemos considerado que
3.3 Simetrías en las Respuestas Ópticas de un Sistema de Dos Niveles
Hemos visto la importancia que tiene el análisis de los parámetros de relajación en las propiedades ópticas. En este contexto óptico se propone una metodología para la estimación de los tiempos de relajación, la cual se basa en algunas propiedades de simetría de las respuestas ópticas no lineales. Estas simetrías son evidentes en el análisis de estas propiedades en función de la desintonización de los haces incidentes definidos en las superficies y las correspondientes curvas de nivel en el espacio de frecuencias. La simetría a la que nos referimos, corresponde al comportamiento de la intensidad de la señal FWM o a las propiedades ópticas no lineales del índice de absorción o refracción, en relación con las frecuencias ópticas asociadas a los haces de bombeo y de prueba. Nuestro modelo se basa en el cálculo de los tiempos de relajación utilizando los ejes mayor y menor de la elipse que representa el coeficiente de absorción después de las transformaciones unitarias, en función de la desintonización de frecuencia de los haces de bombeo y prueba. Consideramos la presencia del baño térmico a través del desplazamiento de la frecuencia del Bohr. De la ec. (4) obtenemos la componente de Fourier de la coherencia en tercer orden en la teoría de la perturbación, expresado como:
Siendo
En donde el coeficiente absortivo
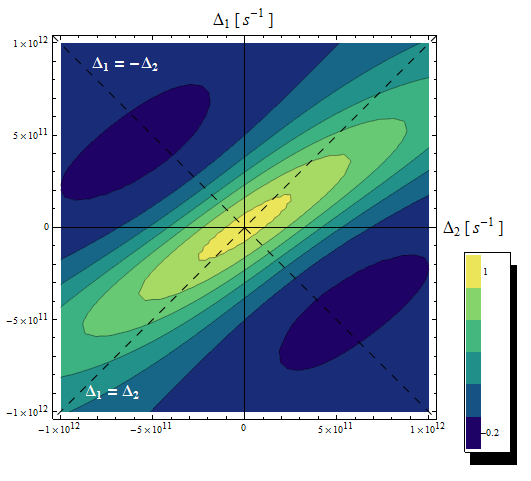
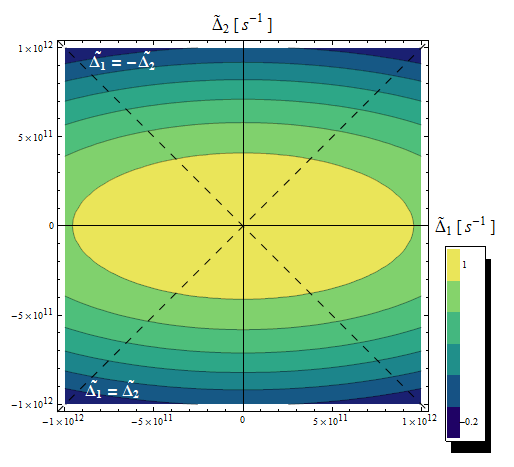
En la Fig. 3 hemos representado el coeficiente de absorción (a) y el índice de refracción (b) no lineal, como función de las desintonizaciones de bombeo y prueba en referencia a la frecuencia de Bohr. Este tipo de representaciones son denominadas propiedades ópticas en el espacio de frecuencias. Para efectos de lo que pretendemos en esta sección, haremos uso de tales representaciones para elucidar de allí algunas propiedades de simetría inherentes a su comportamiento que permita evaluar el tiempo de relajación transversal, que como vimos anteriormente, juega un rol fundamental en la física asociada a estas respuestas ópticas. Con el fin de estudiar tales propiedades, representamos las mismas en función de las desintonizaciones en frecuencia de la forma
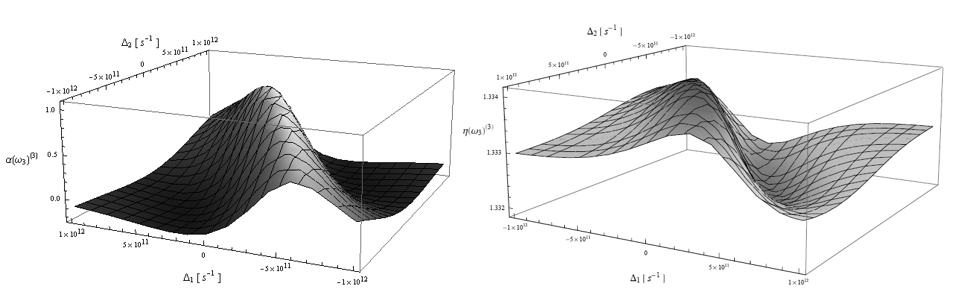
Figura 3. (a) Coeficiente de absorción no lineal y (b) el índice de refracción no lineal, en el espacio de las frecuencias (Δ_1,Δ_2).
En la Fig. 3(b) para el índice de refracción se puede observar que la intensidad global varía poco a lo largo del plano. Realizando las correspondientes sustituciones, se pueden obtener expresiones tanto para el coeficiente de absorción como para el índice de refracción no lineal a la frecuencia indicada, en función de la desintonización de frecuencia, como se indica a continuación:
En la ec. (22) hemos considerado que
En este apartado se propone la determinación de los tiempos de relajación transversal y longitudinal pero en una forma distinta a lo habitual. Para colorantes orgánicos los tiempos de relajación longitudinal y transversal suelen hallarse definiendo el perfil de absorción, pero considerando los anchos medios a la altura media. Típicamente es lo que en óptica o espectroscopia se corresponde con el semi-ancho a la semi-altura (HWHM). Es importante destacar que nuestra propuesta se basa en el comportamiento de las propiedades ópticas no lineales. Por ejemplo, en el caso de los colorantes orgánicos, las relaciones siguientes
Como se puede ver, de los semiejes es posible extraer información de los tiempos de relajación. Este ejemplo de cálculo demuestra cómo al establecer las propiedades de simetría asociadas a las propiedades ópticas no lineales, podemos determinar información útil de los procesos de relajación (Paz y col. 2017). Ahora bien, dado que ambos valores propios dependen exclusivamente de los tiempos de relajación
Este método introduce una importante posibilidad de calcular los tiempos de relajación fundamentales que no requieren una identificación previa del sistema molecular en estudio, en las condiciones del modelo general aquí presentado (Paz y col. 2016, 2017).
3.4 Difusión Espectral y Propiedades Ópticas No Lineales
Los efectos de la difusión espectral sobre la susceptibilidad no lineal de tercer orden para sistemas cuánticos de dos y tres niveles, inmerso en un reservorio térmico, se evalúan con una señal de mezcla de cuatro ondas a través del formalismo de la matriz de densidad. Las ecuaciones ópticas de Bloch se resuelven para un sistema cuántico de dos niveles que permite la relajación en un estado cuántico del reservorio y para un sistema cuántico de tres niveles sin considerar la relajación en el reservorio; en ambos casos, se incluye la difusión espectral. Es decir, se comparan las modificaciones en la respuesta óptica no lineal para el caso en el que el tercer estado |C⟩ del sistema pertenece al reservorio y el caso en el que pertenece al sistema molecular activo. Además, en los modelos cuánticos se utiliza una distribución de la frecuencia natural, que sigue una función lorentziana. De esta manera, se puede investigar el efecto potencial de la relajación cruzada sobre la absorción óptica no lineal y las respuestas de dispersión. Consideramos un modelo de un sistema cuántico de dos niveles no homogéneamente ensanchado (Fig. 6).
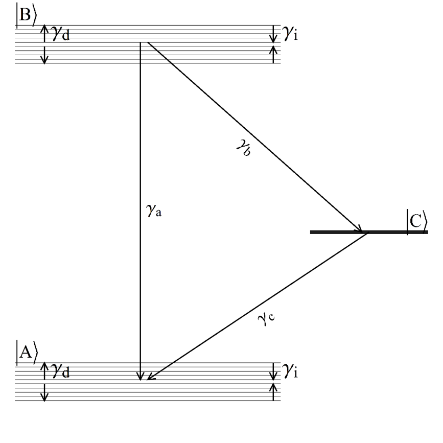
Figura 6. Diagrama de energía para un sistema de dos niveles, el cual incluye la relajación de cruce en los estados bases y excitados. El sistema relaja sobre un estado del reservorio
Para considerar la difusión espectral en este tipo de sistemas y evaluar su incidencia en las respuestas ópticas, resolvemos las ecuaciones de Bloch ópticas convencionales. A diferencia de los casos anteriores, nuestro sistema de estudio contiene un estado del reservorio en el mecanismo de relajación. No explicitamos, como en los casos anteriores, un corrimiento en la frecuencia de Bohr por presencia del baño térmico. En otras palabras, hacemos uso de las ecuaciones de Bloch ópticas convencionales pero a diferencia de los casos anteriores, explicitamos los mecanismos de relajación hacia y dentro de la banda de estados. Necesitamos obtener la coherencia al tercer orden. A través del desarrollo perturbativo, es necesario consolidar las coherencias al primer orden, y con ellas los términos de diferencias poblacionales al segundo orden (Moncada y col. 2018). En este tratamiento, resolvemos los elementos de matriz densidad tanto diagonales como no-diagonales en el espacio de frecuencias. Las coherencias al tercer orden están dadas por:
Γ3 es la velocidad de relajación o inverso al tiempo de relajación de difusión espectral,
En la coherencia dada por la ec. (23) observamos la función de distribución
Obtenemos la susceptibilidad a tercer orden a la frecuencia ω_3, dada por:
Distinguiendo que esta respuesta se corresponde para un sistema de dos estados en presencia del reservorio térmico (2E+R). En la ec. (25) tenemos que:
Se trata de una banda de forma lorentziana centrada en ω_c y con un semi-ancho a la semi-altura dado por el parámetro Γ_4. Es importante además considerar que las cantidades encontradas anteriormente están sujetas al conjunto de condiciones
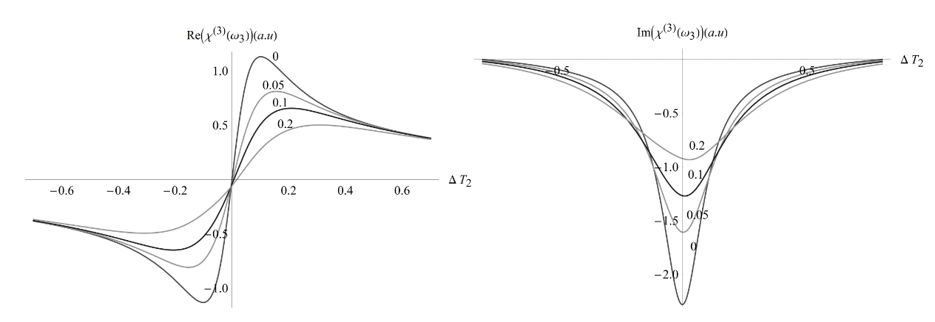
Figura 7. Parte real (a) y parte imaginaria (b) de la susceptibilidad óptica como función del parámetro
Observamos cómo la propiedad dispersiva o absortiva disminuye en su intensidad a medida que aumenta la intensidad de la difusión hacia el estado del reservorio. Notamos que el efecto de contraste dispersivo se hace cada vez más plano con la mayor disipación desde el estado molecular superior. Así mismo, notamos que la absorción neta del estado inferior al superior se hace menor, dado que la energía que se absorbe se disipa inmediatamente hacia el estado del reservorio. En la coherencia a tercer orden a la frecuencia de la señal de FWM, podemos observar que en el caso que no exista difusión espectral entre la banda de los estados moleculares, ni exista el canal de relajación hacia el estado del reservorio térmico, la coherencia se reduce a
Donde
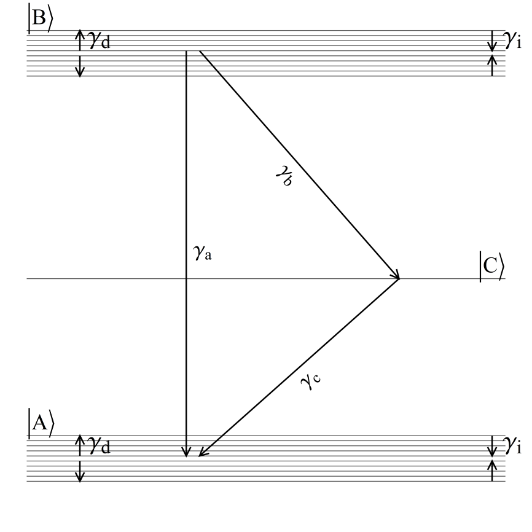
Una representación distinta y más realista corresponde a la representación de los procesos multifotónicos que tienen lugar en un esquema de tres niveles cuánticos. Es decir, a diferencia del caso anterior, consideramos tres estados cuánticos moleculares sin la presencia del estado del reservorio. Conceptualmente, a diferencia del caso anterior, en este caso debemos resolver un sistema matricial de 3x3 donde todos los estados son de la molécula y la presencia del reservorio térmico sólo se explicita a través de los tiempos de relajación longitudinal y transversal. Para ello tenemos el siguiente diagrama (Fig. 8):
En este sistema consideramos como frecuencia de resonancia aquella que se determina desde los puntos medios de cada una de las bandas de los estados moleculares. Ahora, el estado |C⟩ es un canal de relajación de la molécula (estado sin ensanchamiento). Para efectos de cálculo, es necesario que este tercer estado se encuentre lejos de la región de resonancia, referida a las frecuencias de los haces de bombeo y de prueba, pero colocado exactamente a la mitad de la diferencia neta de energía entre los estados moleculares fundamental y excitado. A diferencia del caso anterior, donde es necesario resolver una matriz densidad 2x2 y explicitar la difusión espectral intrabanda y definir la cinética de relajación hacia el estado del reservorio, ahora tenemos que resolver el sistema de la matriz densidad empleando el siguiente conjunto de ecuaciones diferenciales en el dominio del tiempo:
Para j,k,l={a,b,c} y j≠k≠l
Las disminuciones de la tasa de población entre los niveles del sistema se etiquetan como se muestra en la Fig. 8. El inverso de los tiempos de relajación transversal del sistema se denomina
Donde:
En este caso observamos que la coherencia presenta una similitud de carácter analítico con relación a la calculada para el sistema de dos estados en presencia del baño térmico a través del estado |C⟩. La diferencia implícita se corresponde con las funciones f y g en ambos casos. En la función f_3 encontramos un término adicional que da cuenta de la cinética de relajación hacia el tercer estado molecular |C⟩, no existente en el caso anterior. De igual forma, es posible establecer correlaciones entre ambos tratamientos a través de la función g de la forma:
Esta correlación de funciones g, que a su vez puede representar una correlación entre los distintos modelos, es válida en condiciones donde γ_b>γ_c. Resolviendo la integral para la ecuación de polarización y expresando el resultado bajo la forma tensorial, es posible calcular la susceptibilidad óptica de la forma:
Distinguiendo que esta respuesta está referida a un sistema de tres estados (3E). Notamos de igual forma que la forma funcional de esta susceptibilidad es la misma al comparar con el sistema descrito anteriormente. Las propiedades ópticas dispersivas y absortivas calculadas a través de las partes reales e imaginarias de esta susceptibilidad, se representan en las Figs. 9(a) y (b), respectivamente:
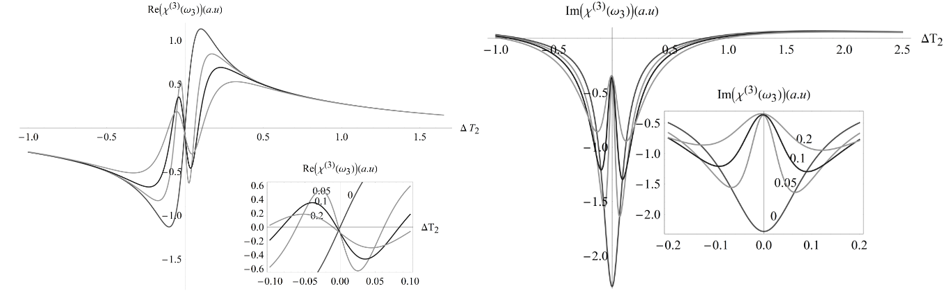
Figura 9. Parte real (a) y parte imaginaria (b) de la susceptibilidad macroscópica en un sistema de tres estados, dos de los cuales se ensanchan para producir el efecto de difusión espectral, bajo las condiciones
La respuesta dispersiva en un sistema de tres niveles muestra dos variaciones repentinas en la región
De los esquemas de cálculo presentados, observamos que las diferencias entre los dos modelos se deben al término
Es decir la ec. (33) se refiere a la correspondencia entre los modelos de sistemas cuánticos de dos estados en presencia del reservorio térmico y el sistema de tres estados moleculares. Si en el sistema de dos estados en presencia del baño térmico eliminamos los efectos de difusión, se recuperaría un sistema de tres estados sin difusión espectral equivalente al presentado por Yajima y col. (1978). De la misma manera, al establecer en ambos modelos la condición
Los modelos analizados de interacción radiación-materia donde se pretende estudiar propiedades ópticas no lineales y caracterizar a través de las mismas los sistemas moleculares complejos, pueden relacionarse adecuadamente a través de la inserción de mecanismos de relajación que conecten el sistema molecular con la presencia del baño térmico. Normalmente este último se lo incluye a través de los tiempos de relajación longitudinales y transversales. Sin embargo, explicitar la presencia del baño térmico bien a través del corrimiento de la frecuencia de Bohr por efectos colisionales, o definirlo como canal de relajación como los presentados en esta sección, ofrece una mayor potencialidad en los estudios, cuando se desea correlacionar las respuestas ópticas con efectos de amplia importancia, como son los sensores ópticos en dispositivos opto-electrónicos.
Finalmente es importante destacar con la metodología presentada que, bajo ciertas condiciones, es muy útil el trabajo con los estados cuánticos a través de la matriz densidad empleando ecuaciones ópticas de Bloch, tanto en forma determinista como estocástica. De igual forma y bajos ciertas condiciones relacionadas a los aspectos cinéticos de los mecanismos de disipación, que tratan (o simular) un sistema de tres estados moleculares, como un sistema de dos estados moleculares y definir la presencia del reservorio térmico como un tercer estado sólo para la relajación, es de suma importancia y de gran utilidad. Correlacionar estas metodologías de estudios de 2E+R con 3E es de importancia dado que reduce considerablemente la forma de cálculo en términos del número de ecuaciones diferenciales a resolver para los elementos de matriz densidad diagonales y no diagonales.
4. COMENTARIOS FINALES
El presente trabajo de revisión pretende dar al lector una visión de distintas formas de caracterización de sistemas moleculares complejos a través de las propiedades ópticas no lineales. En ciertos casos donde la interacción radiación-materia es débil, el sistema puede describirse como un sistema de dos estados y emplear teoría de perturbaciones para la amplitud del campo para tratar las respuestas ópticas en señales de mezclas de cuatro ondas. Sin embargo, cuando el campo perturbador es relativamente intenso, muchos procesos multi-fotónicos suelen presentarse y es necesario estudiar las respuestas ópticas bajo un esquema saturativo. Resolver los problemas de matriz densidad tanto en el dominio del tiempo como en el espacio de frecuencia, tiene cierta significancia cuando lo que se pretende es determinar parámetros específicos del sistema, como son los tiempos de relajación, de altísimo interés en diseños opto-electrónicos. De igual forma, cuando se incluye una variable aleatoria como es el caso presentado de corrimiento de la frecuencia de Bohr a una función dependiente del tiempo, evaluar los promedios en el conjunto estadístico sobre las realizaciones de esta variable, puede presentar un obstáculo complejo. Metodologías propuestas por Van Kampen y col. (1981) –aún vigentes- dan respuesta sencilla a estas dificultades. Hemos presentado una metodología para la determinación de los tiempos de relajación tanto longitudinal como transversal empleando propiedades de simetría intrínsecas en las propiedades ópticas. Equivalencias en ciertas respuestas al invertir una de las desintonizaciones de frecuencia bombeo o prueba, o variación simultánea de ambas desintonizaciones, pueden verse reflejadas en un espacio de frecuencias rotado. Aquí podemos, a partir de las determinaciones de los ejes elípticos mayores y menores, tener información de estos parámetros temporales. Brindar una metodología gráfica sencilla para su determinación, evita esquemas de cálculos más complejos, donde los tiempos de relajación se extraen de los semi-anchos a las semi-alturas máximas en los perfiles ópticos. Finalmente, poder comparar cálculos en sistemas de dos y tres estados con aquellos donde se explicita el estado de reservorio térmico, son de gran utilidad no sólo práctica en el cálculo de las matrices densidad y resolución de ecuaciones ópticas de Bloch, sino de importancia en diseños opto-electrónicos. En lo sucesivo, deseamos implementar un estudio de sistemas moleculares complejos a través de resoluciones temporales de la matriz densidad en presencia de baños térmicos que induzcan una aleatoriedad al sistema, pero considerando bases acopladas o cruce de curvas. En estos casos, buscamos resolver el asunto de los promedios de conjunto, empleando teoremas de Novikov al reconocer la coherencia como un funcional y empleo de ruidos multiplicativos para su solución. Considerar acoplamientos intramoleculares con previa inclusión de Hamiltonianos residuales en el esquema de cálculo, puede dar razón de una mayor y mejor comprensión de los procesos de absorción de dos fotones sin necesidad de abandonar la aproximación de onda rotante.